12.3.1等腰三角形的性质 课件(共42张PPT)
文档属性
| 名称 | 12.3.1等腰三角形的性质 课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 00:00:00 | ||
图片预览







文档简介
(共42张PPT)
12.3.1等腰三角形的性质
第12章 全等三角形
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
等腰三角形的性质教案
一、教学目标
知识与技能目标
学生能够准确说出等腰三角形的定义,清晰理解并熟练掌握等腰三角形两底角相等、三线合一等性质,能够运用这些性质进行简单的几何计算和证明。
过程与方法目标
通过动手裁剪、折叠等腰三角形纸片,经历观察、猜想、验证等腰三角形性质的过程,培养学生的动手操作能力、逻辑推理能力和空间想象能力,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
激发学生对几何图形的探索欲望,增强学生学习数学的兴趣和自信心,培养学生勇于探索、敢于创新的精神,体会数学的对称美和逻辑美。
二、教学重难点
教学重点
等腰三角形 “等边对等角” 和 “三线合一” 性质的探索、理解与应用。
教学难点
等腰三角形 “三线合一” 性质的准确理解和灵活运用,以及性质的证明过程中辅助线的添加方法和逻辑推理思路。
三、教学方法
讲授法、演示法、探究法、讨论法相结合。通过讲授法讲解等腰三角形的基本概念和性质,运用演示法展示等腰三角形的折叠过程,引导学生通过探究法自主发现性质,利用讨论法促进学生之间的交流与合作,深化对知识的理解。
四、教学过程
(一)导入新课(5 分钟)
展示生活中常见的等腰三角形图片,如金字塔、衣架、交通标志等,提问学生:“这些图片中都包含了哪种几何图形?” 引导学生观察并回答出等腰三角形,从而引出本节课的课题 —— 等腰三角形的性质。
回顾三角形的相关知识,提问学生三角形按边分类的情况,进一步明确等腰三角形的定义:有两边相等的三角形叫做等腰三角形。同时介绍等腰三角形的腰、底边、顶角、底角等概念。
(二)探索新知(20 分钟)
动手操作,发现性质
让学生拿出准备好的长方形纸片,按照教材中的步骤裁剪出一个等腰三角形。具体操作如下:将长方形纸片对折,在折痕一侧画一个三角形,使三角形的一条边与折痕重合,另外两条边在长方形纸片上,然后沿所画三角形的边裁剪,展开后得到一个等腰三角形。
引导学生将裁剪好的等腰三角形纸片沿对称轴对折,观察重合的线段和角,提问学生:“通过对折,你发现了等腰三角形的哪些特点?” 鼓励学生大胆猜想等腰三角形可能具有的性质。
组织学生进行小组讨论,分享自己的发现和猜想。教师巡视各小组,倾听学生的讨论,适时给予指导和启发。
各小组派代表汇报讨论结果,教师对学生的猜想进行整理和归纳,引导学生得出等腰三角形的两个重要性质:等腰三角形的两个底角相等(简写成 “等边对等角”);等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成 “三线合一”)。
逻辑推理,证明性质
证明 “等边对等角”
引导学生将文字命题转化为数学符号语言,已知:在△ABC 中,AB = AC。求证:∠B = ∠C。
启发学生思考证明角相等的方法,如全等三角形的性质等。教师提示学生可以通过作辅助线来构造全等三角形,如作顶角平分线 AD、底边上的中线 AD 或底边上的高 AD。
选择作顶角平分线 AD 的方法进行证明,教师在黑板上详细板书证明过程:
证明:作∠BAC 的平分线 AD,
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
AB = AC(已知),
∠BAD = ∠CAD(已证),
AD = AD(公共边),
所以△ABD ≌△ACD(SAS),
所以∠B = ∠C(全等三角形的对应角相等)。
让学生尝试用另外两种作辅助线的方法(作底边上的中线 AD 和底边上的高 AD)进行证明,然后请学生上台板演,其他学生在练习本上完成,教师进行点评和纠正。
证明 “三线合一”
引导学生理解 “三线合一” 的含义,即等腰三角形的顶角平分线、底边上的中线、底边上的高这三条线是同一条线。
已知:在△ABC 中,AB = AC,AD 是∠BAC 的平分线。求证:AD 是 BC 边上的中线和高。
教师引导学生利用已证明的 “等边对等角” 和全等三角形的知识进行证明,学生自主完成证明过程,教师巡视指导,最后展示规范的证明过程。
证明:因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
AB = AC(已知),
∠BAD = ∠CAD(已证),
AD = AD(公共边),
所以△ABD ≌△ACD(SAS),
所以 BD = CD(全等三角形的对应边相等),∠ADB = ∠ADC。
又因为∠ADB + ∠ADC = 180°,所以∠ADB = ∠ADC = 90°,即 AD 是 BC 边上的中线和高。
(三)巩固练习(15 分钟)
基础练习
已知等腰三角形的一个底角是 70°,求它的顶角的度数。
等腰三角形的一个角是 50°,求它的另外两个角的度数。
如图,在△ABC 中,AB = AC,AD 是 BC 边上的高,∠B = 65°,求∠BAD 的度数。
(教师展示题目,学生独立思考并解答,然后请学生回答,教师进行点评和讲解,强调在解决等腰三角形角度问题时,要注意分类讨论。)
拓展练习
如图,在△ABC 中,AB = AC,点 D、E 在 BC 上,且 AD = AE,求证:BD = CE。
(教师引导学生分析题目,鼓励学生尝试多种方法进行证明,如利用 “三线合一” 性质或全等三角形的知识。学生分组讨论并完成证明过程,各小组派代表展示证明方法,教师进行总结和评价。)
(四)课堂小结(5 分钟)
请学生回顾本节课所学的主要内容,包括等腰三角形的定义、性质(“等边对等角” 和 “三线合一”)以及性质的证明方法。
教师对学生的回答进行补充和完善,强调等腰三角形性质的重要性和应用要点,帮助学生构建完整的知识体系。
(五)布置作业(5 分钟)
必做题:教材课后习题第 [X] 题、第 [X] 题,巩固本节课所学的基础知识和基本技能。
选做题:如图,在△ABC 中,AB = AC,D 是 BC 中点,DE⊥AB 于 E,DF⊥AC 于 F,求证:DE = DF。让学有余力的学生进一步拓展思维,提高综合运用知识解决问题的能力。
五、教学反思
在教学过程中,要关注学生的参与度和学习情况,及时发现学生在理解和应用等腰三角形性质过程中存在的问题。对于学生在证明过程中出现的逻辑错误和辅助线添加困难等问题,要进行有针对性的指导和讲解。同时,要鼓励学生积极思考,培养学生的创新意识和实践能力。通过课后作业的反馈,了解学生对知识的掌握程度,以便在后续教学中进行查漏补缺和拓展延伸。
这份教案涵盖了知识讲解与实践应用,希望能满足教学需求。若你对教案环节、难度等有调整需求,欢迎随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、理解并掌握等腰三角形的性质;
2、经历等腰三角形的探究过程,能初步运用等腰三角形的性质解决有关问题;
温故知新
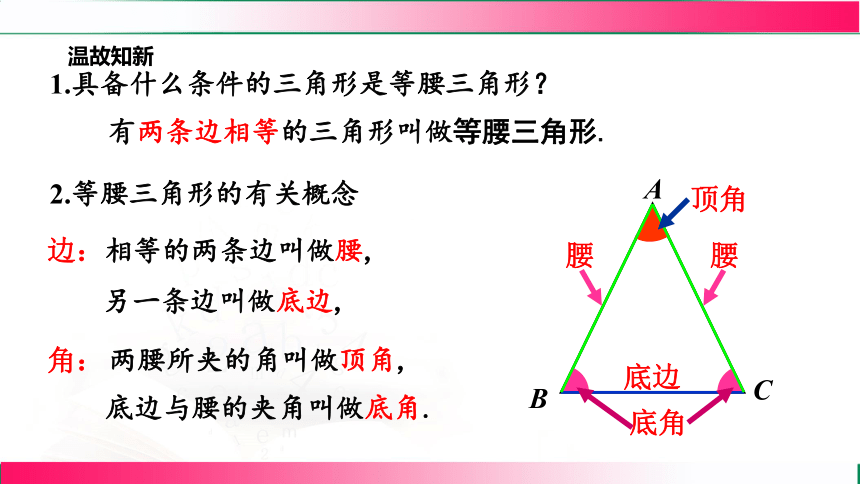
有两条边相等的三角形叫做等腰三角形.
1.具备什么条件的三角形是等腰三角形?
2.等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
法国巴黎的卢浮宫
城市大桥建筑
图片欣赏
知识点一 等腰三角形的性质
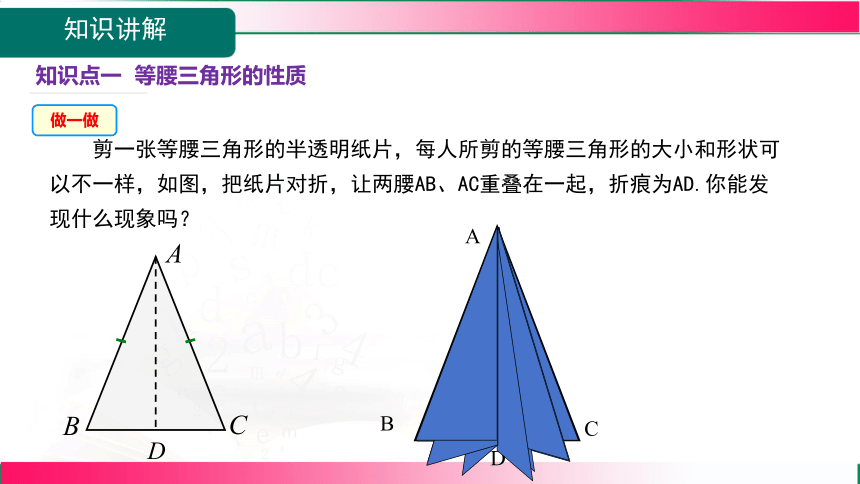
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
做一做
D
A
B
C
1.等腰三角形是轴对称图形.
我们可以得出结论:
A
C
B
D
折痕AD所在直线是等腰三角形的对称轴.
你还有新的发现吗?
∠B,∠C 是等腰三角形的 .
底角
∠B =∠C
所以我们可以描述为:
等腰三角形的两个底角相等.
2.
探究归纳
A
B
C
D
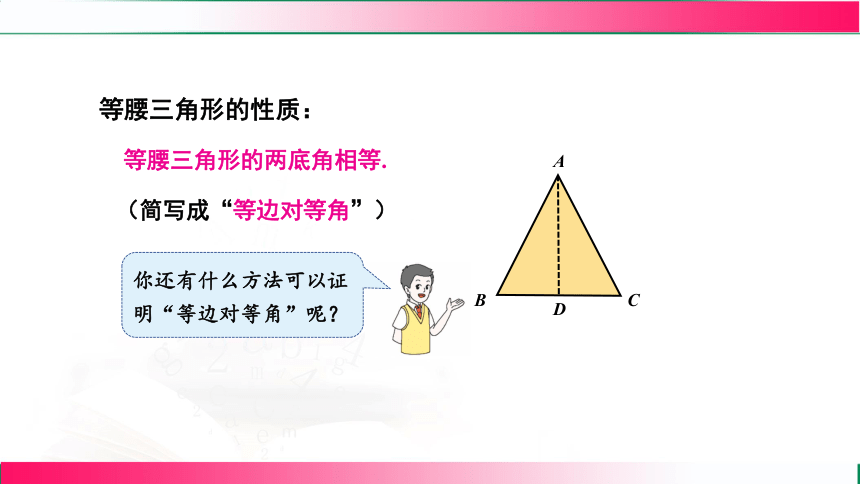
等腰三角形的性质:
等腰三角形的两底角相等.
(简写成“等边对等角”)
你还有什么方法可以证明“等边对等角”呢?
A
B
C
已知:如图,在△ABC中,AB=AC.
求证:∠B =∠C
证明:画∠BAC的平分线AD.
D
1
2
在△ABD和△ACD中,
∵AB=AC(已知)
∠1=∠2(角平分线的定义)
AD=AD(公共边)
∴ △ABD≌△ACD(S.A.S)
∴∠B=∠C(全等三角形的对应角相等)
从这里你还可以得到什么结论?
A
B
C
D
1
2
AD既是底边上的中线,又是顶角的平分线和底边上的高。
A
B
C
D
1
2
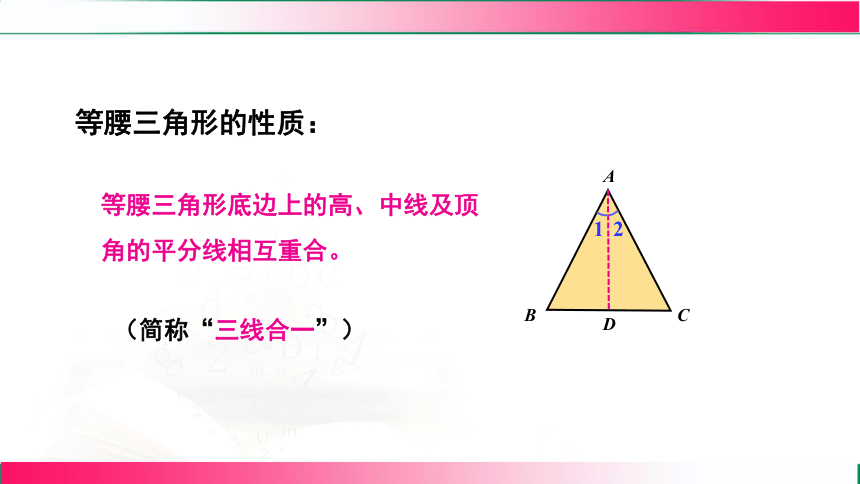
等腰三角形底边上的高、中线及顶角的平分线相互重合。
等腰三角形的性质:
(简称“三线合一”)
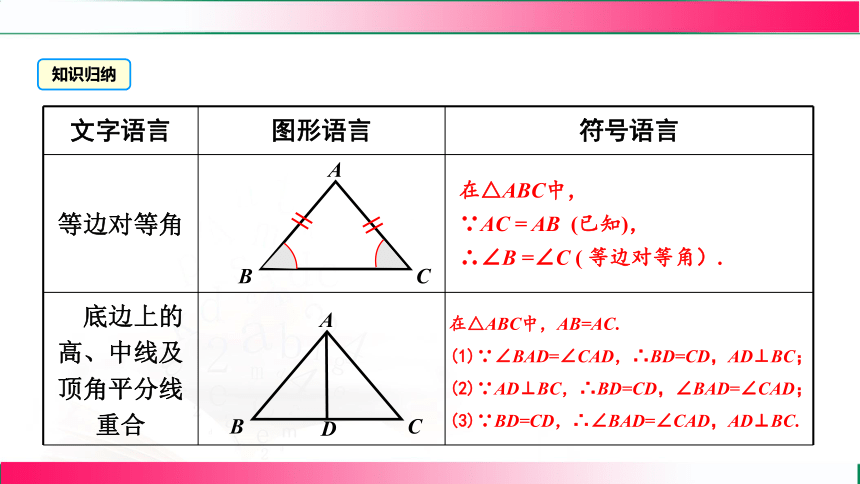
文字语言 图形语言 符号语言
等边对等角
底边上的高、中线及顶角平分线重合
A
B
C
A
B
C
D
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
在△ABC中,AB=AC.
(1)∵∠BAD=∠CAD,∴BD=CD,AD⊥BC;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD;
(3)∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
知识归纳
典例精析
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
1
2
?
?
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
证明:
∵AB=AC,
∴ ∠B= ∠C (等边对等角).
∵D是BC的中点,
∴ DB=DC .
∵DE⊥AB,DF⊥AC,
∴ ∠DEB=∠DFC=90°.
在△DBE和△DCF中,
∴ △DBE ≌ △DCF(AAS).
∴ DE=DF .
练一练
1. 如图,在△ABC中,AB=AC,
(1)如果∠B=70°,那么∠C=____,∠A=____.
A
B
C
D
70°
40°
(2)如果∠A=70°,那么∠B=____,∠C= ___.
(3)如果有一个角等于120°,
那么∠A= ____ ,∠B=___ ,∠C =___ .
(4)如果有一个角等于50°,那么另两个角等于多少度?
55°
55°
120°
30°
30°
解:若∠A=50°,则∠B=∠C=65°;
若∠B=∠C=50°,则∠A=80°.
已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
2. 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
找出图中相等的角并说明理由.
解:∠BAD=∠B=∠C;∠BAC=∠ADB;∠ADC=∠DAC.
∵AD=BD,
∴∠BAD=∠B.
∵AB=AC,
∴∠C=∠B.
∴∠BAD=∠B=∠C
A
B
C
D
∵DC=AC,
∴∠DAC=∠ADC.
∵∠ADB=∠C+∠DAC,
∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC.
3.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
解: (1) ∵AB=AC,BD=DC(已知)
∴∠1=∠2= ∠BAC(三线合一)
∵∠BAC=110°(已知)
∴∠ 1=∠2=55°(等式性质)
知识点二 等边三角形的性质
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B= ∠ C,
同理可得 ∠A=∠B
所以 ∠A=∠B=∠C,
又由 ∠A+∠B+∠C=180°,
从而推出 ∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
A
C
B
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
三条对称轴
A
B
C
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的性质:
正三角形
典例精析
A
B
C
D
例3 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC;
△ABC,
△ABD,
△BCD;
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC与∠A,∠ABD的关系,∠ABC、∠C呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A;
(4)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠ C=180 °,
∴x+2x+2x=180 °.
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
D
1.等腰三角形的对称轴是 ( )
A.底边上的中线 B.顶角的平分线
C.底边上的高 D.底边的垂直平分线
注:对称轴要回答是直线,而ABC三个选项是线段或射线,不符合要求
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是 ( )
A. ∠B=∠C B. AD⊥BC
C. AD平分∠BAC D. AB=2BD
A
B
C
D
D
根据等腰三角形的性质即可证明ABC,D无法说明;
1. 在中,已知 ,若 是等腰三角形,
则 的度数是( )
A. B.
C. 或 D. 或 或
(第2题)
2. 如图,在中, ,
, ,则
( )
A. B. C. D.
√
√
返回
3. [2025长沙岳麓区期中]“一亭幽绝费平章,峡口清风赠
晚凉.前度桃花斗红紫,今来枫叶染丹黄.饶将春色输秋色,
迎过朝阳送夕阳.此地四时可乘兴,待谁招鹤共翱翔.”其中“一
亭”指的是具有一座悠久历史的古典园林建筑——“爱晚亭”.
如图,“爱晚亭”的顶部可看作等腰三角形,,
是边上的一点.下列条件不能说明是 的角平分线
的是( )
(第3题)
A.
B.
C.
D. 与 的周长相等
√
(第3题)
【点拨】A.
,
,
,
是的高线,是等腰三角形, ,
是 的角平分线,故A选项不符合题意;B.
是等腰三角形,,是 的角平分
线,故B选项不符合题意;C.
若,不能说明 是
的角平分线,故C选项
符合题意;D. 与
的周长相等,
,,
是的中线, 是
(第3题)
等腰三角形,是
的角平分线,故D选项不符合
题意.
(第3题)
等腰三角形的“三线
合一”性质的应用:1.等腰三
角形“三线合一”的性质是证明
角相等、线段相等和垂直关系
的既重要又简便的方法.2.“三
线合一”性质是等腰三角形所
特有的性质,它实际是一组定
(第3题)
理,应用过程中,在等腰三角
形前提下,“顶角的平分线、底
边上的中线、底边上的高”只
要知道其中“一线”,就可以说
明是其他“两线”.
(第3题)
返回
4. 定义:等腰三角形的底边长与其腰长的比值
称为这个等腰三角形的“优美比”.若等腰三角形 的两边
长分别是3和9,则它的“优美比” 为__.
5.如图, 的周长为20,且
,于点, 的周
长为16,那么 的长为___.
6
返回
6.[2025上海金山区期末]如图,在
中,为边 上一点,
.
(1)试说明 ;
【解】, ,
.
.
(2)过点作的平行线交 的延长
线于点,若,求证: 平分
.
【证明】, .
,, ,
,平分 .
返回
(第7题)
7. 某平板电脑
支架如图所示,其中
, ,为了使
用的舒适性,可调整 的
大小.若增大 ,则
的变化情况是( )
A. 增大 B. 减小 C. 增大 D. 减小
√
【点拨】, ,
增大 ,
增大 .,减小 .
(第7题)
返回
(第8题)
8.如图,是等腰三角形,点 是底边
上任意一点,, 分别与两边垂直,
等腰三角形的腰长为6,面积为15,则
的值为___.
5
【点拨】连结,如图. ,
,
, .
返回
9.如图钢架中, ,焊上等长的钢条,,
来加固钢架.若 ,则这样的钢条至多需要___根.
3
返回
等腰三角形的性质
底与腰不相等
定义
等边对等角→证明角相等
三线合一
底与腰相等→等边三角形
定义
等腰三角形的所有性质
特有性质:三边相等;三个角都等于60°
谢谢观看!
12.3.1等腰三角形的性质
第12章 全等三角形
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
等腰三角形的性质教案
一、教学目标
知识与技能目标
学生能够准确说出等腰三角形的定义,清晰理解并熟练掌握等腰三角形两底角相等、三线合一等性质,能够运用这些性质进行简单的几何计算和证明。
过程与方法目标
通过动手裁剪、折叠等腰三角形纸片,经历观察、猜想、验证等腰三角形性质的过程,培养学生的动手操作能力、逻辑推理能力和空间想象能力,提高学生分析问题和解决问题的能力。
情感态度与价值观目标
激发学生对几何图形的探索欲望,增强学生学习数学的兴趣和自信心,培养学生勇于探索、敢于创新的精神,体会数学的对称美和逻辑美。
二、教学重难点
教学重点
等腰三角形 “等边对等角” 和 “三线合一” 性质的探索、理解与应用。
教学难点
等腰三角形 “三线合一” 性质的准确理解和灵活运用,以及性质的证明过程中辅助线的添加方法和逻辑推理思路。
三、教学方法
讲授法、演示法、探究法、讨论法相结合。通过讲授法讲解等腰三角形的基本概念和性质,运用演示法展示等腰三角形的折叠过程,引导学生通过探究法自主发现性质,利用讨论法促进学生之间的交流与合作,深化对知识的理解。
四、教学过程
(一)导入新课(5 分钟)
展示生活中常见的等腰三角形图片,如金字塔、衣架、交通标志等,提问学生:“这些图片中都包含了哪种几何图形?” 引导学生观察并回答出等腰三角形,从而引出本节课的课题 —— 等腰三角形的性质。
回顾三角形的相关知识,提问学生三角形按边分类的情况,进一步明确等腰三角形的定义:有两边相等的三角形叫做等腰三角形。同时介绍等腰三角形的腰、底边、顶角、底角等概念。
(二)探索新知(20 分钟)
动手操作,发现性质
让学生拿出准备好的长方形纸片,按照教材中的步骤裁剪出一个等腰三角形。具体操作如下:将长方形纸片对折,在折痕一侧画一个三角形,使三角形的一条边与折痕重合,另外两条边在长方形纸片上,然后沿所画三角形的边裁剪,展开后得到一个等腰三角形。
引导学生将裁剪好的等腰三角形纸片沿对称轴对折,观察重合的线段和角,提问学生:“通过对折,你发现了等腰三角形的哪些特点?” 鼓励学生大胆猜想等腰三角形可能具有的性质。
组织学生进行小组讨论,分享自己的发现和猜想。教师巡视各小组,倾听学生的讨论,适时给予指导和启发。
各小组派代表汇报讨论结果,教师对学生的猜想进行整理和归纳,引导学生得出等腰三角形的两个重要性质:等腰三角形的两个底角相等(简写成 “等边对等角”);等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成 “三线合一”)。
逻辑推理,证明性质
证明 “等边对等角”
引导学生将文字命题转化为数学符号语言,已知:在△ABC 中,AB = AC。求证:∠B = ∠C。
启发学生思考证明角相等的方法,如全等三角形的性质等。教师提示学生可以通过作辅助线来构造全等三角形,如作顶角平分线 AD、底边上的中线 AD 或底边上的高 AD。
选择作顶角平分线 AD 的方法进行证明,教师在黑板上详细板书证明过程:
证明:作∠BAC 的平分线 AD,
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
AB = AC(已知),
∠BAD = ∠CAD(已证),
AD = AD(公共边),
所以△ABD ≌△ACD(SAS),
所以∠B = ∠C(全等三角形的对应角相等)。
让学生尝试用另外两种作辅助线的方法(作底边上的中线 AD 和底边上的高 AD)进行证明,然后请学生上台板演,其他学生在练习本上完成,教师进行点评和纠正。
证明 “三线合一”
引导学生理解 “三线合一” 的含义,即等腰三角形的顶角平分线、底边上的中线、底边上的高这三条线是同一条线。
已知:在△ABC 中,AB = AC,AD 是∠BAC 的平分线。求证:AD 是 BC 边上的中线和高。
教师引导学生利用已证明的 “等边对等角” 和全等三角形的知识进行证明,学生自主完成证明过程,教师巡视指导,最后展示规范的证明过程。
证明:因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
AB = AC(已知),
∠BAD = ∠CAD(已证),
AD = AD(公共边),
所以△ABD ≌△ACD(SAS),
所以 BD = CD(全等三角形的对应边相等),∠ADB = ∠ADC。
又因为∠ADB + ∠ADC = 180°,所以∠ADB = ∠ADC = 90°,即 AD 是 BC 边上的中线和高。
(三)巩固练习(15 分钟)
基础练习
已知等腰三角形的一个底角是 70°,求它的顶角的度数。
等腰三角形的一个角是 50°,求它的另外两个角的度数。
如图,在△ABC 中,AB = AC,AD 是 BC 边上的高,∠B = 65°,求∠BAD 的度数。
(教师展示题目,学生独立思考并解答,然后请学生回答,教师进行点评和讲解,强调在解决等腰三角形角度问题时,要注意分类讨论。)
拓展练习
如图,在△ABC 中,AB = AC,点 D、E 在 BC 上,且 AD = AE,求证:BD = CE。
(教师引导学生分析题目,鼓励学生尝试多种方法进行证明,如利用 “三线合一” 性质或全等三角形的知识。学生分组讨论并完成证明过程,各小组派代表展示证明方法,教师进行总结和评价。)
(四)课堂小结(5 分钟)
请学生回顾本节课所学的主要内容,包括等腰三角形的定义、性质(“等边对等角” 和 “三线合一”)以及性质的证明方法。
教师对学生的回答进行补充和完善,强调等腰三角形性质的重要性和应用要点,帮助学生构建完整的知识体系。
(五)布置作业(5 分钟)
必做题:教材课后习题第 [X] 题、第 [X] 题,巩固本节课所学的基础知识和基本技能。
选做题:如图,在△ABC 中,AB = AC,D 是 BC 中点,DE⊥AB 于 E,DF⊥AC 于 F,求证:DE = DF。让学有余力的学生进一步拓展思维,提高综合运用知识解决问题的能力。
五、教学反思
在教学过程中,要关注学生的参与度和学习情况,及时发现学生在理解和应用等腰三角形性质过程中存在的问题。对于学生在证明过程中出现的逻辑错误和辅助线添加困难等问题,要进行有针对性的指导和讲解。同时,要鼓励学生积极思考,培养学生的创新意识和实践能力。通过课后作业的反馈,了解学生对知识的掌握程度,以便在后续教学中进行查漏补缺和拓展延伸。
这份教案涵盖了知识讲解与实践应用,希望能满足教学需求。若你对教案环节、难度等有调整需求,欢迎随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、理解并掌握等腰三角形的性质;
2、经历等腰三角形的探究过程,能初步运用等腰三角形的性质解决有关问题;
温故知新
有两条边相等的三角形叫做等腰三角形.
1.具备什么条件的三角形是等腰三角形?
2.等腰三角形的有关概念
A
B
C
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
边:
角:
法国巴黎的卢浮宫
城市大桥建筑
图片欣赏
知识点一 等腰三角形的性质
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
做一做
D
A
B
C
1.等腰三角形是轴对称图形.
我们可以得出结论:
A
C
B
D
折痕AD所在直线是等腰三角形的对称轴.
你还有新的发现吗?
∠B,∠C 是等腰三角形的 .
底角
∠B =∠C
所以我们可以描述为:
等腰三角形的两个底角相等.
2.
探究归纳
A
B
C
D
等腰三角形的性质:
等腰三角形的两底角相等.
(简写成“等边对等角”)
你还有什么方法可以证明“等边对等角”呢?
A
B
C
已知:如图,在△ABC中,AB=AC.
求证:∠B =∠C
证明:画∠BAC的平分线AD.
D
1
2
在△ABD和△ACD中,
∵AB=AC(已知)
∠1=∠2(角平分线的定义)
AD=AD(公共边)
∴ △ABD≌△ACD(S.A.S)
∴∠B=∠C(全等三角形的对应角相等)
从这里你还可以得到什么结论?
A
B
C
D
1
2
AD既是底边上的中线,又是顶角的平分线和底边上的高。
A
B
C
D
1
2
等腰三角形底边上的高、中线及顶角的平分线相互重合。
等腰三角形的性质:
(简称“三线合一”)
文字语言 图形语言 符号语言
等边对等角
底边上的高、中线及顶角平分线重合
A
B
C
A
B
C
D
在△ABC中,
∵AC = AB (已知),
∴∠B =∠C ( 等边对等角).
在△ABC中,AB=AC.
(1)∵∠BAD=∠CAD,∴BD=CD,AD⊥BC;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD;
(3)∵BD=CD,∴∠BAD=∠CAD,AD⊥BC.
知识归纳
典例精析
例1 已知:如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,
求证: ∠ADB=∠BAC.
A
B
C
D
1
2
?
?
证明:∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠1(等边对等角)
∴∠C=∠1.
∵∠ADB是△ADC的外角,
∴∠ADB=∠C+∠2.
∴∠ADB=∠1+∠2=∠BAC.
例2 已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F.
求证:DE=DF.
D
A
B
C
F
E
证明:
∵AB=AC,
∴ ∠B= ∠C (等边对等角).
∵D是BC的中点,
∴ DB=DC .
∵DE⊥AB,DF⊥AC,
∴ ∠DEB=∠DFC=90°.
在△DBE和△DCF中,
∴ △DBE ≌ △DCF(AAS).
∴ DE=DF .
练一练
1. 如图,在△ABC中,AB=AC,
(1)如果∠B=70°,那么∠C=____,∠A=____.
A
B
C
D
70°
40°
(2)如果∠A=70°,那么∠B=____,∠C= ___.
(3)如果有一个角等于120°,
那么∠A= ____ ,∠B=___ ,∠C =___ .
(4)如果有一个角等于50°,那么另两个角等于多少度?
55°
55°
120°
30°
30°
解:若∠A=50°,则∠B=∠C=65°;
若∠B=∠C=50°,则∠A=80°.
已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
2. 如图,在△ABC中,点D在BC上,AD=BD,AB=AC=CD.
找出图中相等的角并说明理由.
解:∠BAD=∠B=∠C;∠BAC=∠ADB;∠ADC=∠DAC.
∵AD=BD,
∴∠BAD=∠B.
∵AB=AC,
∴∠C=∠B.
∴∠BAD=∠B=∠C
A
B
C
D
∵DC=AC,
∴∠DAC=∠ADC.
∵∠ADB=∠C+∠DAC,
∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC.
3.如图的房屋人字梁架中,AB=AC ,BD=DC, ∠BAC=110°,
(1) 求∠B、∠C、∠1、∠2的度数;
(2) 求证:AD⊥BC .
(2) 证明:∵AB=AC,BD=DC(已知)
∴ AD⊥BC(三线合一)
1
2
解: (1) ∵AB=AC,BD=DC(已知)
∴∠1=∠2= ∠BAC(三线合一)
∵∠BAC=110°(已知)
∴∠ 1=∠2=55°(等式性质)
知识点二 等边三角形的性质
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B= ∠ C,
同理可得 ∠A=∠B
所以 ∠A=∠B=∠C,
又由 ∠A+∠B+∠C=180°,
从而推出 ∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
A
C
B
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
三条对称轴
A
B
C
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的性质:
正三角形
典例精析
A
B
C
D
例3 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC;
△ABC,
△ABD,
△BCD;
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC与∠A,∠ABD的关系,∠ABC、∠C呢?
∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD,
∠ABC= ∠BDC=2 ∠A,
∠C= ∠BDC=2 ∠A;
(4)设∠A=x,请把△ ABC的内角和用含x的式子表示出来.
∵ ∠A+ ∠ABC+ ∠ C=180 °,
∴x+2x+2x=180 °.
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
D
1.等腰三角形的对称轴是 ( )
A.底边上的中线 B.顶角的平分线
C.底边上的高 D.底边的垂直平分线
注:对称轴要回答是直线,而ABC三个选项是线段或射线,不符合要求
2.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是 ( )
A. ∠B=∠C B. AD⊥BC
C. AD平分∠BAC D. AB=2BD
A
B
C
D
D
根据等腰三角形的性质即可证明ABC,D无法说明;
1. 在中,已知 ,若 是等腰三角形,
则 的度数是( )
A. B.
C. 或 D. 或 或
(第2题)
2. 如图,在中, ,
, ,则
( )
A. B. C. D.
√
√
返回
3. [2025长沙岳麓区期中]“一亭幽绝费平章,峡口清风赠
晚凉.前度桃花斗红紫,今来枫叶染丹黄.饶将春色输秋色,
迎过朝阳送夕阳.此地四时可乘兴,待谁招鹤共翱翔.”其中“一
亭”指的是具有一座悠久历史的古典园林建筑——“爱晚亭”.
如图,“爱晚亭”的顶部可看作等腰三角形,,
是边上的一点.下列条件不能说明是 的角平分线
的是( )
(第3题)
A.
B.
C.
D. 与 的周长相等
√
(第3题)
【点拨】A.
,
,
,
是的高线,是等腰三角形, ,
是 的角平分线,故A选项不符合题意;B.
是等腰三角形,,是 的角平分
线,故B选项不符合题意;C.
若,不能说明 是
的角平分线,故C选项
符合题意;D. 与
的周长相等,
,,
是的中线, 是
(第3题)
等腰三角形,是
的角平分线,故D选项不符合
题意.
(第3题)
等腰三角形的“三线
合一”性质的应用:1.等腰三
角形“三线合一”的性质是证明
角相等、线段相等和垂直关系
的既重要又简便的方法.2.“三
线合一”性质是等腰三角形所
特有的性质,它实际是一组定
(第3题)
理,应用过程中,在等腰三角
形前提下,“顶角的平分线、底
边上的中线、底边上的高”只
要知道其中“一线”,就可以说
明是其他“两线”.
(第3题)
返回
4. 定义:等腰三角形的底边长与其腰长的比值
称为这个等腰三角形的“优美比”.若等腰三角形 的两边
长分别是3和9,则它的“优美比” 为__.
5.如图, 的周长为20,且
,于点, 的周
长为16,那么 的长为___.
6
返回
6.[2025上海金山区期末]如图,在
中,为边 上一点,
.
(1)试说明 ;
【解】, ,
.
.
(2)过点作的平行线交 的延长
线于点,若,求证: 平分
.
【证明】, .
,, ,
,平分 .
返回
(第7题)
7. 某平板电脑
支架如图所示,其中
, ,为了使
用的舒适性,可调整 的
大小.若增大 ,则
的变化情况是( )
A. 增大 B. 减小 C. 增大 D. 减小
√
【点拨】, ,
增大 ,
增大 .,减小 .
(第7题)
返回
(第8题)
8.如图,是等腰三角形,点 是底边
上任意一点,, 分别与两边垂直,
等腰三角形的腰长为6,面积为15,则
的值为___.
5
【点拨】连结,如图. ,
,
, .
返回
9.如图钢架中, ,焊上等长的钢条,,
来加固钢架.若 ,则这样的钢条至多需要___根.
3
返回
等腰三角形的性质
底与腰不相等
定义
等边对等角→证明角相等
三线合一
底与腰相等→等边三角形
定义
等腰三角形的所有性质
特有性质:三边相等;三个角都等于60°
谢谢观看!
