13.1.1直角三角形三边关系 课件(共39张PPT)
文档属性
| 名称 | 13.1.1直角三角形三边关系 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:54:01 | ||
图片预览








文档简介
(共39张PPT)
13.1.1直角三角形三边关系
第13章 勾股定理
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
直角三角形三边关系教案
一、教学目标
(一)知识与技能目标
学生能够准确理解勾股定理的内容,熟练掌握直角三角形三边之间的数量关系,即两直角边的平方和等于斜边的平方(\(a^2 + b^2 = c^2\),其中\(a\)、\(b\)为直角边,\(c\)为斜边)。
能够灵活运用勾股定理进行简单的计算,包括已知两边求第三边,以及解决实际生活中的相关问题。
(二)过程与方法目标
通过观察、猜想、操作、验证等一系列数学探究活动,培养学生的自主探究能力和逻辑推理能力。
在探究勾股定理的过程中,让学生体会从特殊到一般的数学思维方法,提高学生分析问题和解决问题的能力。
(三)情感态度与价值观目标
激发学生对数学的好奇心和求知欲,增强学生学习数学的兴趣和信心。
让学生在探究活动中体验成功的喜悦,培养学生的合作精神和创新意识,感受数学文化的魅力。
二、教学重难点
(一)教学重点
勾股定理的内容及其推导过程。
勾股定理的简单应用,包括在直角三角形中已知两边求第三边。
(二)教学难点
勾股定理的推导过程,尤其是通过图形面积的方法证明勾股定理。
灵活运用勾股定理解决实际问题,培养学生将实际问题转化为数学问题的能力。
三、教学方法
讲授法、探究法、讨论法、直观演示法相结合
四、教学过程
(一)情境导入(5 分钟)
展示图片:展示生活中含有直角三角形的物体图片,如梯子、三角板、房屋的屋顶等,引导学生观察这些物体中的直角三角形。
提出问题:“同学们,我们看到这些直角三角形在生活中随处可见。那么,直角三角形的三条边之间除了长短不同,是否还存在着某种特殊的数量关系呢?今天我们就一起来探索这个问题。”
(二)探究新知(20 分钟)
特殊直角三角形探究(8 分钟)
课件展示边长为 3、4、5 的直角三角形,引导学生计算三条边的平方:\(3^2 = 9\),\(4^2 = 16\),\(5^2 = 25\)。
组织学生小组讨论:观察这三个平方数,你能发现它们之间有什么关系吗?
小组代表发言,教师总结:\(3^2 + 4^2 = 9 + 16 = 25 = 5^2\),即两条直角边的平方和等于斜边的平方。
再展示边长为 5、12、13 的直角三角形,让学生自主计算验证上述关系是否成立。
一般直角三角形探究(12 分钟)
利用方格纸,画出两直角边分别为\(a\)、\(b\),斜边为\(c\)的一般直角三角形(\(a\)、\(b\)为整数)。
以直角三角形的三条边为边长向外作正方形,引导学生通过数方格的方法计算三个正方形的面积(对于不满一格的采用割补法)。
设两直角边对应的正方形面积分别为\(S_1\)、\(S_2\),斜边对应的正方形面积为\(S_3\),让学生观察并猜想\(S_1\)、\(S_2\)、\(S_3\)之间的关系。
小组讨论交流后,教师引导学生得出:\(S_1 + S_2 = S_3\),进而得到\(a^2 + b^2 = c^2\)。
多媒体动态演示多个不同的直角三角形,验证上述结论的普遍性。
(三)定理推导(10 分钟)
介绍赵爽弦图:通过多媒体展示赵爽弦图,向学生介绍其历史背景和文化意义,激发学生的民族自豪感。
证明过程:
引导学生观察弦图,将大正方形分割成四个全等的直角三角形和一个小正方形。
设直角三角形的两直角边分别为\(a\)、\(b\),斜边为\(c\),分别表示出大正方形的面积(\(c^2\))和四个直角三角形与小正方形的面积之和\((4\times\frac{1}{2}ab + (b - a)^2)\)。
通过面积相等列出等式:\(c^2 = 4\times\frac{1}{2}ab + (b - a)^2\),化简后得到\(a^2 + b^2 = c^2\),从而证明勾股定理。
(四)例题讲解(10 分钟)
例 1:在直角三角形中,已知两直角边分别为\(6\)和\(8\),求斜边的长。
分析:直接运用勾股定理\(a^2 + b^2 = c^2\),其中\(a = 6\),\(b = 8\),求\(c\)。
解答过程:\(c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\)。
例 2:在直角三角形中,已知斜边为\(13\),一条直角边为\(5\),求另一条直角边的长。
分析:同样运用勾股定理,变形为\(b = \sqrt{c^2 - a^2}\)(设\(c\)为斜边,\(a\)、\(b\)为直角边),其中\(c = 13\),\(a = 5\),求\(b\)。
解答过程:\(b = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12\)。
强调:在使用勾股定理计算时,要注意分清斜边和直角边,避免计算错误。
(五)课堂练习(10 分钟)
基础练习:
直角三角形的两直角边分别为\(3\)和\(4\),则斜边为______。
直角三角形的斜边为\(10\),一条直角边为\(6\),则另一条直角边为______。
提高练习:
一个门框的尺寸如图所示,一块长\(3m\),宽\(2.2m\)的长方形薄木板能否从门框内通过?为什么?(门框高\(2m\),宽\(1m\))
让学生独立完成练习,教师巡视指导,及时发现学生存在的问题并进行针对性讲解。
(六)课堂小结(5 分钟)
提问学生:“今天我们学习了什么知识?你有哪些收获?”
教师总结:回顾勾股定理的内容、推导过程和应用,强调勾股定理在直角三角形三边关系中的重要性,以及从特殊到一般的数学探究方法。
(七)作业布置(1 分钟)
必做题:课本习题 [具体页码] 第 [X]、[X]、[X] 题。
选做题:查阅资料,了解勾股定理的其他证明方法,并尝试自己证明。
五、教学资源
多媒体课件,包含相关图片、动画和演示内容。
方格纸、三角板、直尺等学习工具。
六、教学反思
在教学过程中,要关注学生的参与度和理解程度,及时调整教学节奏和方法。对于勾股定理的推导过程,部分学生可能理解起来有困难,需要加强引导和解释。通过作业和后续练习,进一步了解学生对知识的掌握情况,针对薄弱环节进行强化辅导。
这份教案涵盖了知识讲解与实践应用。你可以说说对教案各环节的看法,比如是否需要增减练习难度,我来进一步优化。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、掌握勾股定理及其简单应用,理解定理的一般探究方法;
2、通过利用方格纸计算面积的方法探索勾股定理,经历观察、归纳、猜想和验证的数学发现过程,发展数形结合的数学思想;
你知道2002年在北京召开的国际数学家大会(ICM-2002)吗?在这次大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
1955年希腊发行的一枚纪念邮票.
这张邮票是纪念二千五百年前希腊的一个学派和宗教团体──毕达哥拉斯学派.
邮票上的图案是根据一个著名的数学定理设计的.
观察这枚邮票上的图案,数数图案中各正方形中小方格的个数,你有什么猜想?
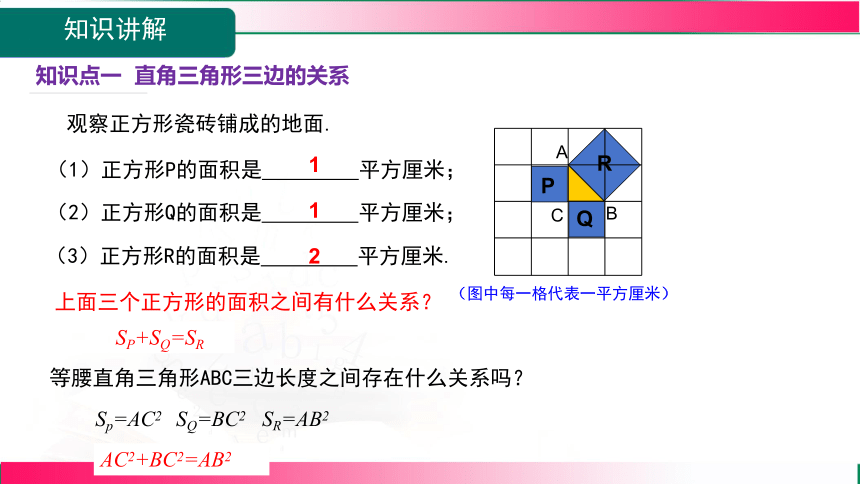
知识点一 直角三角形三边的关系
(图中每一格代表一平方厘米)
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
观察正方形瓷砖铺成的地面.
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢
想一想
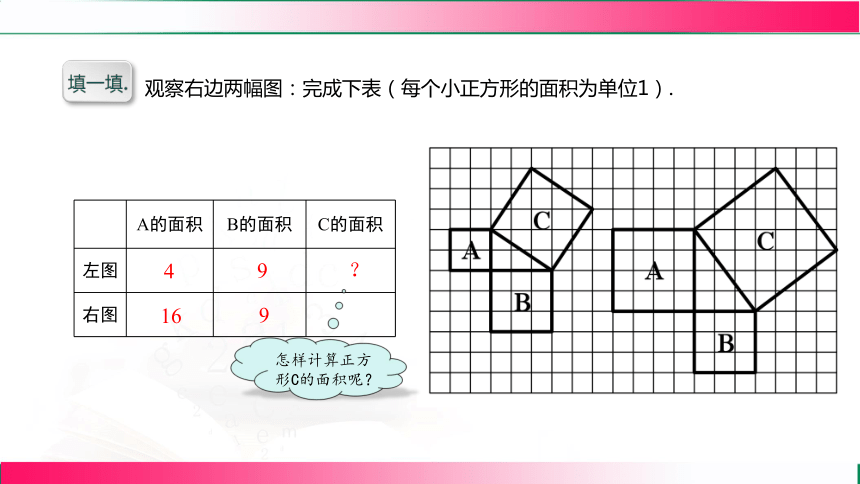
填一填.
观察右边两幅图:完成下表(每个小正方形的面积为单位1).
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
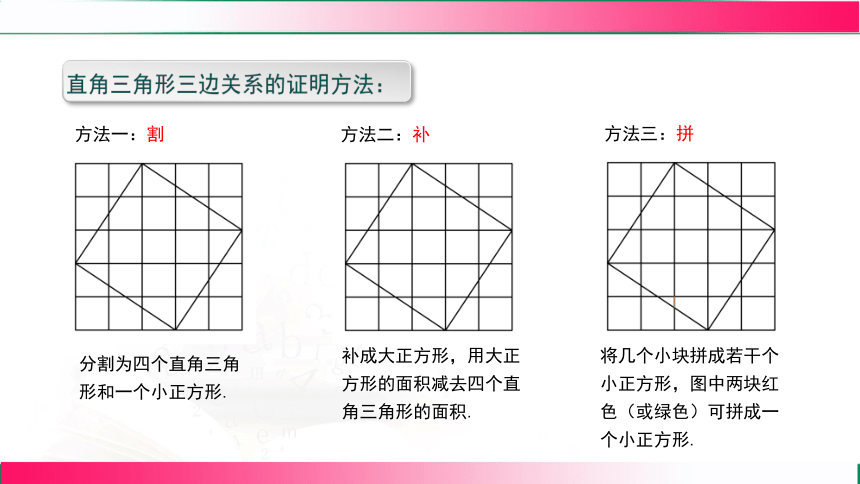
直角三角形三边关系的证明方法:
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
分析表中数据,你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
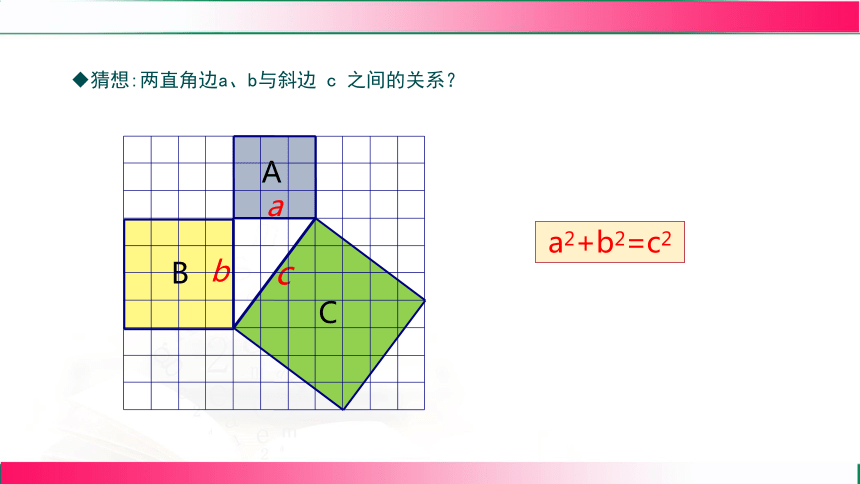
猜想:两直角边a、b与斜边 c 之间的关系?
A
B
C
a
c
b
a2+b2=c2
由上面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2,
a
b
c
这种关系我们称为勾股定理.
即 直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
概念总结
思考:怎样证明勾股定理?
左图是弦图的示意图,它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.
大正方形的面积=c2.
四个全等的直角三角形和小正方形的面积之和= .
即a2+b2=c2.
做
一
做
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,也能证明勾股定理.请你试一试,写出完整的证明过程.
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积之和= .
由题可知(a+b)2=2ab+c2,
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
典例精析
【例1】求出下列直角三角形中未知边的长度.
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
x2 =100
x2=62+82
∵x>0,
y2+52=132
y2=132-52
y2=144
∴ y=12.
(2)在Rt△ABC中,由勾股定理得:
AC2+BC2=AB2
∵y>0,
A
6
8
x
C
B
5
y
13
C
A
B
∴ x=10.
(1)
(2)
练一练
(1)在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=________;
(2)在Rt△ABC中,∠C=90°,AB=25,AC=20,则BC=________;
(3)在Rt△ABC中,∠C=90°,它的两边是6和8,则它的第三边长是________.
13
15
10或
2.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
3.如图,以Rt△ABC的三条边为直径的半圆的面积分别为S1、S2、S3,已知S1=9,S3=25,求S2.
解:由图形可得
S1=π()2=,
S2=π()2=,
S3=π()2=,
AB2+AC2=BC2,∴S1+S2=(AC2+AB2)=BC2=S3 .
∴S2=S3-S1=25-9=16.
勾股图中的面积关系:
以直角三角形的三边为基础,分别向外作半圆、正方形、等边三角形,如图,它们都形成了简单的勾股图. 对于这些勾股图,它们都具有相同的结论,即S3=S1+S2. 与直角三角形三边相连的图形还可以换成正五边形、正六边形等,结论同样成立.
1.求下列图中未知数x、y、z的值.
x=15
y=5
z=7
81
16
x
y
144
169
z
625
576
2. 如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
C
B
A
3.如图,正方形中的数据表示它的面积,则第三个正方形的面积为( )
A.69 B.18 C.19 D.20
C
25
44
A
B
C
1. 下列说法中正确的是( )
C
A. 已知,,是三角形的三边长,则
B. 在直角三角形中,两边的平方和等于第三边的平方
C. 在中, ,,,是,, 的对边,所
以
D. 在中, ,,,是,, 的对边,所
以
返回
(第2题)
2. 象棋是中
国的传统棋种,如图所示的象棋棋盘
中,各个小正方形的边长均为1.“马”
从图中的位置出发,按照“马走日”的
规则,走一步之后的落点与“帅”的最
大距离是( )
A
A. 5 B. C. D.
3. 若在直角三角形中,有两边长分别是3和4,
则第三边长为_______.
5或
返回
(第4题)
4.如图,点,分别在, 上,
,垂足为, .若
,,则点到直线 的距离
为___.
(第4题)
【点拨】 ,
,即 ,
,
.设点到直线
的距离为, ,
, .
返回
5.如图,在中,于点,点为 上一点,连
结,,的延长线交于点,已知 ,
.
(1)试说明: .
【解】, , 易得
为等腰直角三角形,
. .又
, ,
, ,
.又
, ,
, , .
(2)利用图中阴影部分面积完成勾股定
理的验证.已知:如图,在 中,
,,, ,试
说明: .
, ,
,,, .
返回
6. 如图,在
中, ,分别以各边为直径
作半圆,图中阴影部分在数学史上称为
“希波克拉底月牙”,当,
时,阴影部分的面积为( )
C
A. 12 B. 13 C. 14 D. 15
【点拨】 在 中,
, ,, 由
勾股定理,得
,
阴影部分的面积为 .
返回
7. [2025沧州期末]意大利著
名画家达·芬奇用如图所示的
方法证明了勾股定理.若设图①
C
A. B.
C. D.
中空白部分的面积为,图②中空白部分的面积为 ,则下
列等式成立的是( )
返回
8.如图,已知 ,且
,,,则 的长是____.
10
(第8题)
【点拨】如图,过作,交的延长线于点 ,则
, ,
在中,, .
返回
(第9题)
9. 如图,
将腰长为2的等腰直角三角形
放置于数轴上,直角边
与数轴重合,直角顶点 与
重合,为的中点,以为圆心, 长为半径画弧,交
数轴于点(在点右侧),则点 表示的数为_______.
勾股定理
定理
验证
1.求边长、面积,证明线段之间的平方关系
2.勾股定理的实际应用
应用
直角三角形两直角边的平方和等于斜边的平方
用拼图法验证勾股定理
谢谢观看!
13.1.1直角三角形三边关系
第13章 勾股定理
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
直角三角形三边关系教案
一、教学目标
(一)知识与技能目标
学生能够准确理解勾股定理的内容,熟练掌握直角三角形三边之间的数量关系,即两直角边的平方和等于斜边的平方(\(a^2 + b^2 = c^2\),其中\(a\)、\(b\)为直角边,\(c\)为斜边)。
能够灵活运用勾股定理进行简单的计算,包括已知两边求第三边,以及解决实际生活中的相关问题。
(二)过程与方法目标
通过观察、猜想、操作、验证等一系列数学探究活动,培养学生的自主探究能力和逻辑推理能力。
在探究勾股定理的过程中,让学生体会从特殊到一般的数学思维方法,提高学生分析问题和解决问题的能力。
(三)情感态度与价值观目标
激发学生对数学的好奇心和求知欲,增强学生学习数学的兴趣和信心。
让学生在探究活动中体验成功的喜悦,培养学生的合作精神和创新意识,感受数学文化的魅力。
二、教学重难点
(一)教学重点
勾股定理的内容及其推导过程。
勾股定理的简单应用,包括在直角三角形中已知两边求第三边。
(二)教学难点
勾股定理的推导过程,尤其是通过图形面积的方法证明勾股定理。
灵活运用勾股定理解决实际问题,培养学生将实际问题转化为数学问题的能力。
三、教学方法
讲授法、探究法、讨论法、直观演示法相结合
四、教学过程
(一)情境导入(5 分钟)
展示图片:展示生活中含有直角三角形的物体图片,如梯子、三角板、房屋的屋顶等,引导学生观察这些物体中的直角三角形。
提出问题:“同学们,我们看到这些直角三角形在生活中随处可见。那么,直角三角形的三条边之间除了长短不同,是否还存在着某种特殊的数量关系呢?今天我们就一起来探索这个问题。”
(二)探究新知(20 分钟)
特殊直角三角形探究(8 分钟)
课件展示边长为 3、4、5 的直角三角形,引导学生计算三条边的平方:\(3^2 = 9\),\(4^2 = 16\),\(5^2 = 25\)。
组织学生小组讨论:观察这三个平方数,你能发现它们之间有什么关系吗?
小组代表发言,教师总结:\(3^2 + 4^2 = 9 + 16 = 25 = 5^2\),即两条直角边的平方和等于斜边的平方。
再展示边长为 5、12、13 的直角三角形,让学生自主计算验证上述关系是否成立。
一般直角三角形探究(12 分钟)
利用方格纸,画出两直角边分别为\(a\)、\(b\),斜边为\(c\)的一般直角三角形(\(a\)、\(b\)为整数)。
以直角三角形的三条边为边长向外作正方形,引导学生通过数方格的方法计算三个正方形的面积(对于不满一格的采用割补法)。
设两直角边对应的正方形面积分别为\(S_1\)、\(S_2\),斜边对应的正方形面积为\(S_3\),让学生观察并猜想\(S_1\)、\(S_2\)、\(S_3\)之间的关系。
小组讨论交流后,教师引导学生得出:\(S_1 + S_2 = S_3\),进而得到\(a^2 + b^2 = c^2\)。
多媒体动态演示多个不同的直角三角形,验证上述结论的普遍性。
(三)定理推导(10 分钟)
介绍赵爽弦图:通过多媒体展示赵爽弦图,向学生介绍其历史背景和文化意义,激发学生的民族自豪感。
证明过程:
引导学生观察弦图,将大正方形分割成四个全等的直角三角形和一个小正方形。
设直角三角形的两直角边分别为\(a\)、\(b\),斜边为\(c\),分别表示出大正方形的面积(\(c^2\))和四个直角三角形与小正方形的面积之和\((4\times\frac{1}{2}ab + (b - a)^2)\)。
通过面积相等列出等式:\(c^2 = 4\times\frac{1}{2}ab + (b - a)^2\),化简后得到\(a^2 + b^2 = c^2\),从而证明勾股定理。
(四)例题讲解(10 分钟)
例 1:在直角三角形中,已知两直角边分别为\(6\)和\(8\),求斜边的长。
分析:直接运用勾股定理\(a^2 + b^2 = c^2\),其中\(a = 6\),\(b = 8\),求\(c\)。
解答过程:\(c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\)。
例 2:在直角三角形中,已知斜边为\(13\),一条直角边为\(5\),求另一条直角边的长。
分析:同样运用勾股定理,变形为\(b = \sqrt{c^2 - a^2}\)(设\(c\)为斜边,\(a\)、\(b\)为直角边),其中\(c = 13\),\(a = 5\),求\(b\)。
解答过程:\(b = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12\)。
强调:在使用勾股定理计算时,要注意分清斜边和直角边,避免计算错误。
(五)课堂练习(10 分钟)
基础练习:
直角三角形的两直角边分别为\(3\)和\(4\),则斜边为______。
直角三角形的斜边为\(10\),一条直角边为\(6\),则另一条直角边为______。
提高练习:
一个门框的尺寸如图所示,一块长\(3m\),宽\(2.2m\)的长方形薄木板能否从门框内通过?为什么?(门框高\(2m\),宽\(1m\))
让学生独立完成练习,教师巡视指导,及时发现学生存在的问题并进行针对性讲解。
(六)课堂小结(5 分钟)
提问学生:“今天我们学习了什么知识?你有哪些收获?”
教师总结:回顾勾股定理的内容、推导过程和应用,强调勾股定理在直角三角形三边关系中的重要性,以及从特殊到一般的数学探究方法。
(七)作业布置(1 分钟)
必做题:课本习题 [具体页码] 第 [X]、[X]、[X] 题。
选做题:查阅资料,了解勾股定理的其他证明方法,并尝试自己证明。
五、教学资源
多媒体课件,包含相关图片、动画和演示内容。
方格纸、三角板、直尺等学习工具。
六、教学反思
在教学过程中,要关注学生的参与度和理解程度,及时调整教学节奏和方法。对于勾股定理的推导过程,部分学生可能理解起来有困难,需要加强引导和解释。通过作业和后续练习,进一步了解学生对知识的掌握情况,针对薄弱环节进行强化辅导。
这份教案涵盖了知识讲解与实践应用。你可以说说对教案各环节的看法,比如是否需要增减练习难度,我来进一步优化。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、掌握勾股定理及其简单应用,理解定理的一般探究方法;
2、通过利用方格纸计算面积的方法探索勾股定理,经历观察、归纳、猜想和验证的数学发现过程,发展数形结合的数学思想;
你知道2002年在北京召开的国际数学家大会(ICM-2002)吗?在这次大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
1955年希腊发行的一枚纪念邮票.
这张邮票是纪念二千五百年前希腊的一个学派和宗教团体──毕达哥拉斯学派.
邮票上的图案是根据一个著名的数学定理设计的.
观察这枚邮票上的图案,数数图案中各正方形中小方格的个数,你有什么猜想?
知识点一 直角三角形三边的关系
(图中每一格代表一平方厘米)
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
观察正方形瓷砖铺成的地面.
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢
想一想
填一填.
观察右边两幅图:完成下表(每个小正方形的面积为单位1).
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
直角三角形三边关系的证明方法:
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
分析表中数据,你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
猜想:两直角边a、b与斜边 c 之间的关系?
A
B
C
a
c
b
a2+b2=c2
由上面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2,
a
b
c
这种关系我们称为勾股定理.
即 直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
概念总结
思考:怎样证明勾股定理?
左图是弦图的示意图,它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.
大正方形的面积=c2.
四个全等的直角三角形和小正方形的面积之和= .
即a2+b2=c2.
做
一
做
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,也能证明勾股定理.请你试一试,写出完整的证明过程.
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积之和= .
由题可知(a+b)2=2ab+c2,
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
典例精析
【例1】求出下列直角三角形中未知边的长度.
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
x2 =100
x2=62+82
∵x>0,
y2+52=132
y2=132-52
y2=144
∴ y=12.
(2)在Rt△ABC中,由勾股定理得:
AC2+BC2=AB2
∵y>0,
A
6
8
x
C
B
5
y
13
C
A
B
∴ x=10.
(1)
(2)
练一练
(1)在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=________;
(2)在Rt△ABC中,∠C=90°,AB=25,AC=20,则BC=________;
(3)在Rt△ABC中,∠C=90°,它的两边是6和8,则它的第三边长是________.
13
15
10或
2.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
3.如图,以Rt△ABC的三条边为直径的半圆的面积分别为S1、S2、S3,已知S1=9,S3=25,求S2.
解:由图形可得
S1=π()2=,
S2=π()2=,
S3=π()2=,
AB2+AC2=BC2,∴S1+S2=(AC2+AB2)=BC2=S3 .
∴S2=S3-S1=25-9=16.
勾股图中的面积关系:
以直角三角形的三边为基础,分别向外作半圆、正方形、等边三角形,如图,它们都形成了简单的勾股图. 对于这些勾股图,它们都具有相同的结论,即S3=S1+S2. 与直角三角形三边相连的图形还可以换成正五边形、正六边形等,结论同样成立.
1.求下列图中未知数x、y、z的值.
x=15
y=5
z=7
81
16
x
y
144
169
z
625
576
2. 如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
C
B
A
3.如图,正方形中的数据表示它的面积,则第三个正方形的面积为( )
A.69 B.18 C.19 D.20
C
25
44
A
B
C
1. 下列说法中正确的是( )
C
A. 已知,,是三角形的三边长,则
B. 在直角三角形中,两边的平方和等于第三边的平方
C. 在中, ,,,是,, 的对边,所
以
D. 在中, ,,,是,, 的对边,所
以
返回
(第2题)
2. 象棋是中
国的传统棋种,如图所示的象棋棋盘
中,各个小正方形的边长均为1.“马”
从图中的位置出发,按照“马走日”的
规则,走一步之后的落点与“帅”的最
大距离是( )
A
A. 5 B. C. D.
3. 若在直角三角形中,有两边长分别是3和4,
则第三边长为_______.
5或
返回
(第4题)
4.如图,点,分别在, 上,
,垂足为, .若
,,则点到直线 的距离
为___.
(第4题)
【点拨】 ,
,即 ,
,
.设点到直线
的距离为, ,
, .
返回
5.如图,在中,于点,点为 上一点,连
结,,的延长线交于点,已知 ,
.
(1)试说明: .
【解】, , 易得
为等腰直角三角形,
. .又
, ,
, ,
.又
, ,
, , .
(2)利用图中阴影部分面积完成勾股定
理的验证.已知:如图,在 中,
,,, ,试
说明: .
, ,
,,, .
返回
6. 如图,在
中, ,分别以各边为直径
作半圆,图中阴影部分在数学史上称为
“希波克拉底月牙”,当,
时,阴影部分的面积为( )
C
A. 12 B. 13 C. 14 D. 15
【点拨】 在 中,
, ,, 由
勾股定理,得
,
阴影部分的面积为 .
返回
7. [2025沧州期末]意大利著
名画家达·芬奇用如图所示的
方法证明了勾股定理.若设图①
C
A. B.
C. D.
中空白部分的面积为,图②中空白部分的面积为 ,则下
列等式成立的是( )
返回
8.如图,已知 ,且
,,,则 的长是____.
10
(第8题)
【点拨】如图,过作,交的延长线于点 ,则
, ,
在中,, .
返回
(第9题)
9. 如图,
将腰长为2的等腰直角三角形
放置于数轴上,直角边
与数轴重合,直角顶点 与
重合,为的中点,以为圆心, 长为半径画弧,交
数轴于点(在点右侧),则点 表示的数为_______.
勾股定理
定理
验证
1.求边长、面积,证明线段之间的平方关系
2.勾股定理的实际应用
应用
直角三角形两直角边的平方和等于斜边的平方
用拼图法验证勾股定理
谢谢观看!
