13.1.2直角三角形的判定 课件(共37张PPT)
文档属性
| 名称 | 13.1.2直角三角形的判定 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:55:21 | ||
图片预览









文档简介
(共37张PPT)
13.1.2直角三角形的判定
第13章 勾股定理
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
直角三角形的判定教案
一、教学目标
(一)知识与技能目标
学生能清晰阐述直角三角形的判定方法,熟练掌握勾股定理逆定理的内容,即若三角形三边\(a\)、\(b\)、\(c\)满足\(a^{2}+b^{2}=c^{2}\),则该三角形为直角三角形;同时理解并掌握直角三角形全等的判定定理(HL)。
能够根据给定条件,准确运用上述判定方法判断一个三角形是否为直角三角形,以及判定两个直角三角形是否全等,并解决相关计算和证明问题。
(二)过程与方法目标
通过对勾股定理逆定理的探究,经历观察、猜想、验证、归纳的数学过程,培养学生的逻辑推理能力和逆向思维能力。
在直角三角形全等判定的学习中,通过对比一般三角形全等判定方法,提升学生的知识迁移能力和分析辨别能力。
(三)情感态度与价值观目标
激发学生对数学定理探索的兴趣,让学生在探究过程中感受数学的严谨性和科学性,增强学习数学的自信心。
培养学生合作交流的意识,体会数学知识在实际生活中的广泛应用,提高学生运用数学知识解决实际问题的积极性。
二、教学重难点
(一)教学重点
勾股定理逆定理的理解、推导及应用。
直角三角形全等判定定理(HL)的应用,以及与一般三角形全等判定方法的区别与联系。
(二)教学难点
勾股定理逆定理的证明过程,理解从三边数量关系到三角形形状判定的逻辑关系。
准确区分不同判定方法的适用条件,在实际问题中灵活选择合适的判定方法判断直角三角形及证明全等。
三、教学方法
讲授法、探究法、讨论法、对比分析法相结合
四、教学过程
(一)复习导入(5 分钟)
提问回顾:引导学生回顾直角三角形的定义、性质,以及勾股定理的内容(直角三角形两直角边的平方和等于斜边的平方)。
引发思考:提出问题 “如果已知一个三角形三边的长度,能否通过三边关系判断它是不是直角三角形呢?”,从而引出本节课的学习内容 —— 直角三角形的判定。
(二)勾股定理逆定理的探究与学习(15 分钟)
创设情境,提出猜想(5 分钟)
展示三组三角形的边长数据:①\(3\)、\(4\)、\(5\);②\(5\)、\(12\)、\(13\);③\(6\)、\(8\)、\(10\)。
让学生计算每组数据中三边的平方,并观察它们之间的关系,同时使用三角板或量角器测量三角形的最大角。
组织学生小组讨论,引导学生猜想:如果三角形三边满足两短边的平方和等于最长边的平方,那么这个三角形可能是直角三角形。
验证猜想,推导定理(8 分钟)
利用几何画板动态演示:任意构造一个三边满足\(a^{2}+b^{2}=c^{2}\)的三角形,通过测量工具展示其最大角为\(90^{\circ}\),多组数据验证后,增强学生对猜想的可信度。
进行严谨的证明:已知在\(\triangle ABC\)中,\(BC = a\),\(AC = b\),\(AB = c\),且\(a^{2}+b^{2}=c^{2}\)。作\(Rt\triangle A'B'C'\),使\(\angle C' = 90^{\circ}\),\(B'C' = a\),\(A'C' = b\),根据勾股定理可得\(A'B'^{2}=a^{2}+b^{2}\),又因为\(a^{2}+b^{2}=c^{2}\),所以\(A'B' = c\)。由 “SSS” 可证\(\triangle ABC\cong\triangle A'B'C'\),从而得出\(\angle C = \angle C' = 90^{\circ}\),即\(\triangle ABC\)是直角三角形,证明勾股定理逆定理。
归纳总结(2 分钟)
师生共同总结勾股定理逆定理的内容、符号语言及作用:如果三角形的三边长\(a\)、\(b\)、\(c\)满足\(a^{2}+b^{2}=c^{2}\),那么这个三角形是直角三角形,可用于判定三角形是否为直角三角形。
(三)直角三角形全等判定定理(HL)的学习(12 分钟)
回顾旧知,引发冲突(3 分钟)
提问学生一般三角形全等的判定方法(SSS、SAS、ASA、AAS),并展示两个直角三角形,已知它们的斜边和一条直角边对应相等,让学生尝试用已学判定方法证明全等,发现无法直接证明,产生认知冲突,从而引出直角三角形特殊的全等判定方法。
探究 HL 判定定理(6 分钟)
动手操作:给学生发放画有斜边为\(5cm\),一条直角边为\(3cm\)的直角三角形的纸张,让学生剪下三角形,与同桌的三角形进行比较,观察是否全等。
多媒体演示:通过动画展示多个斜边和一条直角边对应相等的直角三角形,发现它们都能完全重合。
总结归纳:引导学生总结直角三角形全等的判定定理(HL):斜边和一条直角边对应相等的两个直角三角形全等。强调该定理只适用于直角三角形,且必须是斜边和直角边对应相等。
对比辨析(3 分钟)
列表对比一般三角形全等判定方法和 HL 定理的适用条件、特点,让学生填写表格并小组讨论,加深对不同判定方法的理解,明确何时使用 HL 定理判定直角三角形全等。
(四)例题讲解(10 分钟)
勾股定理逆定理应用例题(5 分钟)
例 1:判断以线段\(a = 15\),\(b = 8\),\(c = 17\)为边的三角形是否为直角三角形。
分析:计算三边平方,\(a^{2}=15^{2}=225\),\(b^{2}=8^{2}=64\),\(c^{2}=17^{2}=289\),因为\(a^{2}+b^{2}=225 + 64 = 289 = c^{2}\),根据勾股定理逆定理,可判定该三角形是直角三角形。
HL 定理应用例题(5 分钟)
例 2:如图,已知\(AB = CD\),\(DE\perp AC\),\(BF\perp AC\),垂足分别为\(E\)、\(F\),且\(DE = BF\),求证\(Rt\triangle ABF\cong Rt\triangle CDE\)。
分析:因为\(DE\perp AC\),\(BF\perp AC\),所以\(\triangle ABF\)和\(\triangle CDE\)都是直角三角形。在\(Rt\triangle ABF\)和\(Rt\triangle CDE\)中,\(AB = CD\)(已知),\(BF = DE\)(已知),根据 HL 定理,可证\(Rt\triangle ABF\cong Rt\triangle CDE\)。
(五)课堂练习(10 分钟)
基础练习:
判断下列三角形是否为直角三角形:①\(a = 2\),\(b = 3\),\(c = 4\);②\(a = 9\),\(b = 12\),\(c = 15\)。
如图,\(AC = AD\),\(\angle C = \angle D = 90^{\circ}\),求证\(BC = BD\)。
提高练习:
一个三角形的三边之比为\(3:4:5\),这个三角形是直角三角形吗?为什么?
在\(\triangle ABC\)中,\(AB = 13\),\(BC = 10\),\(BC\)边上的中线\(AD = 12\),判断\(\triangle ABC\)的形状,并说明理由。
学生独立完成练习,教师巡视指导,选取有代表性的学生解答进行展示,讲解解题思路和方法,纠正学生存在的问题。
(六)课堂小结(5 分钟)
提问学生:“本节课我们学习了哪些直角三角形的判定方法?勾股定理逆定理和 HL 定理的应用条件分别是什么?”
教师总结:回顾勾股定理逆定理和 HL 定理的内容、应用,强调判定直角三角形及证明直角三角形全等时的注意事项,梳理本节课的知识要点和学习方法。
(七)作业布置(1 分钟)
必做题:课本习题 [具体页码] 第 [X]、[X]、[X] 题。
选做题:已知\(a\)、\(b\)、\(c\)是\(\triangle ABC\)的三边,且满足\((a - 5)^{2}+(b - 12)^{2}+(c - 13)^{2}=0\),试判断\(\triangle ABC\)的形状,并说明理由。
这份教案围绕多种判定方法展开教学。你若觉得某个环节的讲解深度、练习数量不合适,或者有其他修改方向,都能随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、了解直角三角形的判定条件;
2、能够运用勾股数解决简单实际问题;
温故知新
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
反过来,
如果一个三角形的两边平方和等于第三边的平方,那么这个三角形是直角三角形吗?
勾股定理的概念
思考:同学们你们知道古埃及人用什么方法得到直角的吗
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
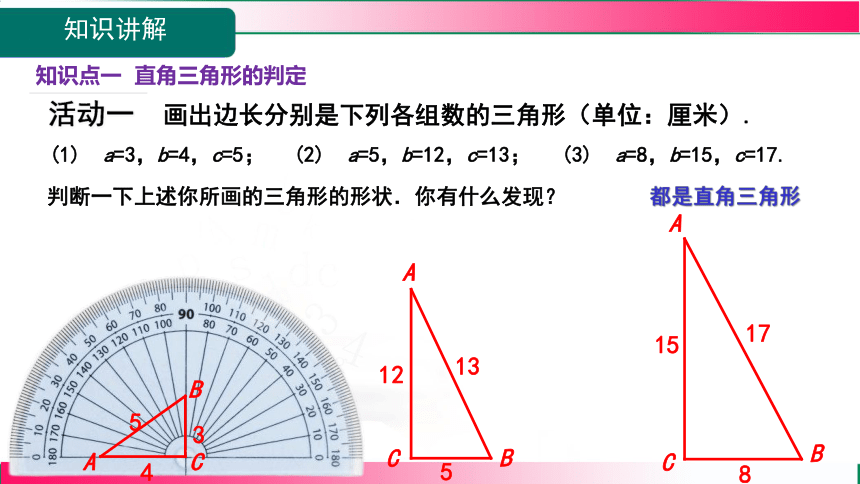
知识点一 直角三角形的判定
活动一 画出边长分别是下列各组数的三角形(单位:厘米).
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
B
3
4
C
A
5
B
5
12
C
A
13
B
8
15
C
A
17
判断一下上述你所画的三角形的形状.你有什么发现?
都是直角三角形
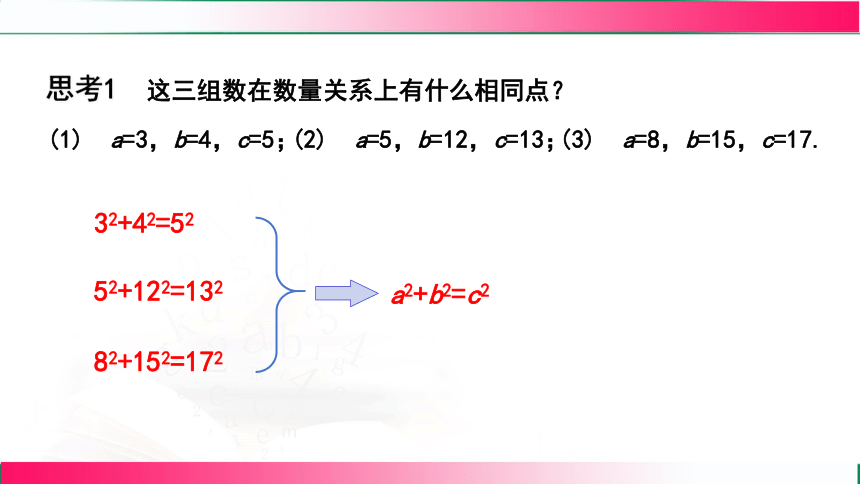
思考1 这三组数在数量关系上有什么相同点?
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
82+152=172
32+42=52
52+122=132
a2+b2=c2
思考2 根据上述结论你有什么猜想呢?
猜想:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
你能证明这个猜想吗?
A
b
a
C
B
c
已知:在△ABC中,AB=c , BC=a, CA=b, 且a2+b2=c2.
求证:△ ABC是直角三角形.
A
b
a
C
B
c
A′
b
a
C′
B′
∟
证明:画一个△A′B′C′,使∠C′=90°,B′C′=a, A′C′=b(如图).
由勾股定理,可得 A′B′ 2= a2+b2.
因为 AB2= a2+b2,
根据“SSS”,可证△ABC ≌△A′ B′ C′ .
于是,∠C=∠C′=90°,△ABC是直角三角形.
勾股定理逆定理
∵在△ABC中,a2+b2=c2,
b
B
A
C
a
c
∟
定理揭示了三角形三边之间的数量关系:a2+b2=c2 → Rt△.
如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.
几何语言:
∴△ABC是直角三角形,且∠C=90°.
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角 ,最长边所对角为直角.
特别说明:
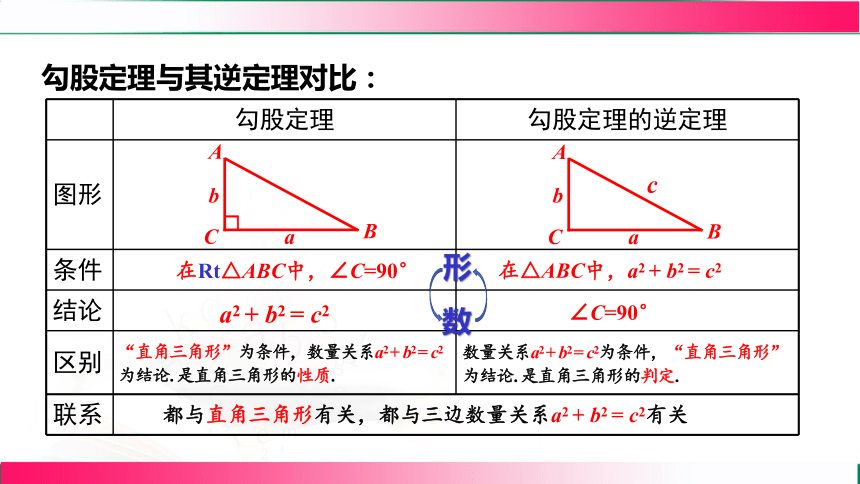
勾股定理与其逆定理对比:
勾股定理 勾股定理的逆定理
图形
条件
结论
区别
联系 A
b
a
C
B
∟
在Rt△ABC中,∠C=90°
a2 + b2 = c2
“直角三角形”为条件,数量关系a2 + b2 = c2为结论. 是直角三角形的性质.
A
b
a
C
B
c
都与直角三角形有关,都与三边数量关系a2 + b2 = c2有关
在△ABC中,a2 + b2 = c2
∠C=90°
数量关系a2 + b2 = c2为条件,“直角三角形”为结论. 是直角三角形的判定.
形
数
典例精析
(1) a=8,b=15,c=17;
(2) a=13,b=14,c=15.
【例1】下面以a、b、c为边长的三角形是不是直角三角形?若是,请指出哪个角是直角.
解:(1) ∵82+152=64+225=289,172=289,
∴ 82+152=172.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
(2) ∵132+142=365,152=225,
∴ 132+142≠152,不符合勾股定理的逆定理,
∴ 这个三角形不是直角三角形.
【例2】已知△ABC,AB=n2-1,BC=2n,AC=n2+1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由.
解:∵AB2+BC2=(n2-1)2+(2n)2
=n4-2n2+1+4n4
=n4+2n2+1
=(n2+1)2
=AC2,
∴△ABC是直角三角形,边AC所对的角是直角.
想一想,为什么选择AB2+BC2?AB、BC、CA的大小关系是怎样的?
练一练
(1) a=7,b=25,c=24;
1、判断由a、b、c组成的三角形是不是直角三角形,若是,请指出哪个角是直角.
(2) a:b:c=3:4:5.
解:(1) ∵72+242=49+576=625,252=625,
∴ 72+242=252.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠B是直角.
(2)设a=3k、b=4k、c=5k,
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
2、一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,你说这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
知识点二 常见的勾股数
满足a2+b2=c2的三个正整数, 称为勾股数。
常见的基本勾股数有:
3,4,5;
6,8,10;
5,12,13;
8,15,17;
7,24,25;
9,40,41;
1.“勾股数”的任意正整数倍仍是勾股数。
2.判断勾股数的方法:
(1)确定是不是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的平方.
3.易错警示:勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方.
典例精析
【例3】 下列各组数是勾股数的是( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132
A
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
练一练
1、像(3,4,5)、(6,8,10)、(5,12,13)等满足a2+b2=c2的三个正整数,通常称为勾股数,请你填表并探索规律.
a 3 6 9 12 … 3n
b 4 8 12 16 … 4n
c 5 10 15 20 … 5n
a 3 5 7 9 11 … 2n+1
b 4 12 24 40 60 … 2n(n+1)
c 5 13 25 41 61 … 2n(n+1)+1
①从上面2个表中你能发现什么规律?
②你能根据发现的规律写出更多的勾股数吗?试试看 .
解:①规律:一组勾股数,都扩大相同倍数n(n为正整数),得到一组新数,这组数同样是勾股数.
勾股数的性质
②答案不唯一,如:15,20,25;13,84,85等.
利用勾股数可以构造直角三角形.
1.设三角形的三边长分别等于下列各组数,试判断各三角形是否是直角三角形.若是,指出哪一条边所对的角是直角.
(1) 12,16,20; (2) 1.5,2,2.5.
解:(1)因为122+162=400=202,所以是直角三角形,且边长为20的边所对的角为直角.
(2)因为1.52+22=2.52,所以是直角三角形,且边长为2.5的边所对的角为直角.
2.若一个三角形的三条边长a、b、c满足a2=c2-b2,则这个三角形是直角三角形吗?
解:因为a2=c2-b2,所以a2+b2=c2,所以这个三角形是直角三角形.
3.以下各组数为边长,能组成直角三角形的是( ).
A.5,6,7 B.10,8,4
C.7,25,24 D.9,17,15
4.以下各组正数为边长,能组成直角三角形的是( ).
A. B.
C. D.
C
B
1. 四根小棒的长分别是5,9,12,13,从
中任意选择三根小棒首尾相接,搭成边长如下的四个三角形,
其中是直角三角形的是( )
C
A. 5,9,12 B. 5,9,13
C. 5,12,13 D. 9,12,13
2. 若三角形的三边长分别为,, ,且满足
,则此三角形中最大的角是( )
B
A. 锐角 B. 直角 C. 钝角 D. 无法确定
返回
3. 如图,有四个三角形,各有一边长为6,一边长为8,若第
三边长分别为6,8,10,12,则面积最大的三角形是( )
C
A. B. C. D.
返回
(第4题)
4. [2025西安雁塔区月考]如图,在
由小正方形组成的 网格中,每个
小正方形的顶点称为格点.点, ,
,,,均在格点上,点, ,
,中能与点, 构成一个直角三角
形的是( )
D
A. 点 B. 点 C. 点 D. 点
返回
(第5题)
5.如图,在四边形 中,
, , ,
,则 的度数为______.
【点拨】连结, ,
,
是等边三角形,
, . ,
,
,
, .
(第5题)
返回
6.[2025徐州期中]如图,把一块 土地划出一个
后,测得米,米, 米,
米,其中 .
(1)判断 的形状,并说明理由;
【解】 是直角三角形.
理由: , 米,
米,
(米).
又米,米, ,
是直角三角形, .
(2)求图中阴影部分的面积.
阴影部分的面积
(平方米).
返回
7. [2025常州期末]下列由三条线段,,构成的三角形
其内角分别为,,:; ,
,; ;
,,为大于1的整数 ,其
中能构成直角三角形的是( )
B
A. ①④ B. ①②④ C. ②③④ D. ①②③
【点拨】, ,
, , 能构成直角三角形;
, ,
, 能构成直角三角形;
, ,
, 不能构成直角三角形;
, ,
, 能构成直角三角形. 能构成直角三角形
的是①②④.
已知三角形三边的长,常常借助勾股定理的逆定理
来探究三角形是不是直角三角形.在利用公式 时
一定要注意是最大边,即 .
返回
8.如图,在正方形网格中,每个小正方形
的边长都是1个单位长度,点,, ,
,均在小正方形的顶点上,线段 ,
交于点,若 ,则 等
于________.(结果用含 的式子表示)
直角三角形的判定
勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形
勾股数:满足a2+b2=c2的三个正整数
谢谢观看!
13.1.2直角三角形的判定
第13章 勾股定理
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
直角三角形的判定教案
一、教学目标
(一)知识与技能目标
学生能清晰阐述直角三角形的判定方法,熟练掌握勾股定理逆定理的内容,即若三角形三边\(a\)、\(b\)、\(c\)满足\(a^{2}+b^{2}=c^{2}\),则该三角形为直角三角形;同时理解并掌握直角三角形全等的判定定理(HL)。
能够根据给定条件,准确运用上述判定方法判断一个三角形是否为直角三角形,以及判定两个直角三角形是否全等,并解决相关计算和证明问题。
(二)过程与方法目标
通过对勾股定理逆定理的探究,经历观察、猜想、验证、归纳的数学过程,培养学生的逻辑推理能力和逆向思维能力。
在直角三角形全等判定的学习中,通过对比一般三角形全等判定方法,提升学生的知识迁移能力和分析辨别能力。
(三)情感态度与价值观目标
激发学生对数学定理探索的兴趣,让学生在探究过程中感受数学的严谨性和科学性,增强学习数学的自信心。
培养学生合作交流的意识,体会数学知识在实际生活中的广泛应用,提高学生运用数学知识解决实际问题的积极性。
二、教学重难点
(一)教学重点
勾股定理逆定理的理解、推导及应用。
直角三角形全等判定定理(HL)的应用,以及与一般三角形全等判定方法的区别与联系。
(二)教学难点
勾股定理逆定理的证明过程,理解从三边数量关系到三角形形状判定的逻辑关系。
准确区分不同判定方法的适用条件,在实际问题中灵活选择合适的判定方法判断直角三角形及证明全等。
三、教学方法
讲授法、探究法、讨论法、对比分析法相结合
四、教学过程
(一)复习导入(5 分钟)
提问回顾:引导学生回顾直角三角形的定义、性质,以及勾股定理的内容(直角三角形两直角边的平方和等于斜边的平方)。
引发思考:提出问题 “如果已知一个三角形三边的长度,能否通过三边关系判断它是不是直角三角形呢?”,从而引出本节课的学习内容 —— 直角三角形的判定。
(二)勾股定理逆定理的探究与学习(15 分钟)
创设情境,提出猜想(5 分钟)
展示三组三角形的边长数据:①\(3\)、\(4\)、\(5\);②\(5\)、\(12\)、\(13\);③\(6\)、\(8\)、\(10\)。
让学生计算每组数据中三边的平方,并观察它们之间的关系,同时使用三角板或量角器测量三角形的最大角。
组织学生小组讨论,引导学生猜想:如果三角形三边满足两短边的平方和等于最长边的平方,那么这个三角形可能是直角三角形。
验证猜想,推导定理(8 分钟)
利用几何画板动态演示:任意构造一个三边满足\(a^{2}+b^{2}=c^{2}\)的三角形,通过测量工具展示其最大角为\(90^{\circ}\),多组数据验证后,增强学生对猜想的可信度。
进行严谨的证明:已知在\(\triangle ABC\)中,\(BC = a\),\(AC = b\),\(AB = c\),且\(a^{2}+b^{2}=c^{2}\)。作\(Rt\triangle A'B'C'\),使\(\angle C' = 90^{\circ}\),\(B'C' = a\),\(A'C' = b\),根据勾股定理可得\(A'B'^{2}=a^{2}+b^{2}\),又因为\(a^{2}+b^{2}=c^{2}\),所以\(A'B' = c\)。由 “SSS” 可证\(\triangle ABC\cong\triangle A'B'C'\),从而得出\(\angle C = \angle C' = 90^{\circ}\),即\(\triangle ABC\)是直角三角形,证明勾股定理逆定理。
归纳总结(2 分钟)
师生共同总结勾股定理逆定理的内容、符号语言及作用:如果三角形的三边长\(a\)、\(b\)、\(c\)满足\(a^{2}+b^{2}=c^{2}\),那么这个三角形是直角三角形,可用于判定三角形是否为直角三角形。
(三)直角三角形全等判定定理(HL)的学习(12 分钟)
回顾旧知,引发冲突(3 分钟)
提问学生一般三角形全等的判定方法(SSS、SAS、ASA、AAS),并展示两个直角三角形,已知它们的斜边和一条直角边对应相等,让学生尝试用已学判定方法证明全等,发现无法直接证明,产生认知冲突,从而引出直角三角形特殊的全等判定方法。
探究 HL 判定定理(6 分钟)
动手操作:给学生发放画有斜边为\(5cm\),一条直角边为\(3cm\)的直角三角形的纸张,让学生剪下三角形,与同桌的三角形进行比较,观察是否全等。
多媒体演示:通过动画展示多个斜边和一条直角边对应相等的直角三角形,发现它们都能完全重合。
总结归纳:引导学生总结直角三角形全等的判定定理(HL):斜边和一条直角边对应相等的两个直角三角形全等。强调该定理只适用于直角三角形,且必须是斜边和直角边对应相等。
对比辨析(3 分钟)
列表对比一般三角形全等判定方法和 HL 定理的适用条件、特点,让学生填写表格并小组讨论,加深对不同判定方法的理解,明确何时使用 HL 定理判定直角三角形全等。
(四)例题讲解(10 分钟)
勾股定理逆定理应用例题(5 分钟)
例 1:判断以线段\(a = 15\),\(b = 8\),\(c = 17\)为边的三角形是否为直角三角形。
分析:计算三边平方,\(a^{2}=15^{2}=225\),\(b^{2}=8^{2}=64\),\(c^{2}=17^{2}=289\),因为\(a^{2}+b^{2}=225 + 64 = 289 = c^{2}\),根据勾股定理逆定理,可判定该三角形是直角三角形。
HL 定理应用例题(5 分钟)
例 2:如图,已知\(AB = CD\),\(DE\perp AC\),\(BF\perp AC\),垂足分别为\(E\)、\(F\),且\(DE = BF\),求证\(Rt\triangle ABF\cong Rt\triangle CDE\)。
分析:因为\(DE\perp AC\),\(BF\perp AC\),所以\(\triangle ABF\)和\(\triangle CDE\)都是直角三角形。在\(Rt\triangle ABF\)和\(Rt\triangle CDE\)中,\(AB = CD\)(已知),\(BF = DE\)(已知),根据 HL 定理,可证\(Rt\triangle ABF\cong Rt\triangle CDE\)。
(五)课堂练习(10 分钟)
基础练习:
判断下列三角形是否为直角三角形:①\(a = 2\),\(b = 3\),\(c = 4\);②\(a = 9\),\(b = 12\),\(c = 15\)。
如图,\(AC = AD\),\(\angle C = \angle D = 90^{\circ}\),求证\(BC = BD\)。
提高练习:
一个三角形的三边之比为\(3:4:5\),这个三角形是直角三角形吗?为什么?
在\(\triangle ABC\)中,\(AB = 13\),\(BC = 10\),\(BC\)边上的中线\(AD = 12\),判断\(\triangle ABC\)的形状,并说明理由。
学生独立完成练习,教师巡视指导,选取有代表性的学生解答进行展示,讲解解题思路和方法,纠正学生存在的问题。
(六)课堂小结(5 分钟)
提问学生:“本节课我们学习了哪些直角三角形的判定方法?勾股定理逆定理和 HL 定理的应用条件分别是什么?”
教师总结:回顾勾股定理逆定理和 HL 定理的内容、应用,强调判定直角三角形及证明直角三角形全等时的注意事项,梳理本节课的知识要点和学习方法。
(七)作业布置(1 分钟)
必做题:课本习题 [具体页码] 第 [X]、[X]、[X] 题。
选做题:已知\(a\)、\(b\)、\(c\)是\(\triangle ABC\)的三边,且满足\((a - 5)^{2}+(b - 12)^{2}+(c - 13)^{2}=0\),试判断\(\triangle ABC\)的形状,并说明理由。
这份教案围绕多种判定方法展开教学。你若觉得某个环节的讲解深度、练习数量不合适,或者有其他修改方向,都能随时和我说。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、了解直角三角形的判定条件;
2、能够运用勾股数解决简单实际问题;
温故知新
勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
反过来,
如果一个三角形的两边平方和等于第三边的平方,那么这个三角形是直角三角形吗?
勾股定理的概念
思考:同学们你们知道古埃及人用什么方法得到直角的吗
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子就得到一个直角三角形, 其直角在第4个结处.
知识点一 直角三角形的判定
活动一 画出边长分别是下列各组数的三角形(单位:厘米).
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
B
3
4
C
A
5
B
5
12
C
A
13
B
8
15
C
A
17
判断一下上述你所画的三角形的形状.你有什么发现?
都是直角三角形
思考1 这三组数在数量关系上有什么相同点?
(2) a=5,b=12,c=13;
(3) a=8,b=15,c=17.
(1) a=3,b=4,c=5;
82+152=172
32+42=52
52+122=132
a2+b2=c2
思考2 根据上述结论你有什么猜想呢?
猜想:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.
你能证明这个猜想吗?
A
b
a
C
B
c
已知:在△ABC中,AB=c , BC=a, CA=b, 且a2+b2=c2.
求证:△ ABC是直角三角形.
A
b
a
C
B
c
A′
b
a
C′
B′
∟
证明:画一个△A′B′C′,使∠C′=90°,B′C′=a, A′C′=b(如图).
由勾股定理,可得 A′B′ 2= a2+b2.
因为 AB2= a2+b2,
根据“SSS”,可证△ABC ≌△A′ B′ C′ .
于是,∠C=∠C′=90°,△ABC是直角三角形.
勾股定理逆定理
∵在△ABC中,a2+b2=c2,
b
B
A
C
a
c
∟
定理揭示了三角形三边之间的数量关系:a2+b2=c2 → Rt△.
如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.
几何语言:
∴△ABC是直角三角形,且∠C=90°.
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角 ,最长边所对角为直角.
特别说明:
勾股定理与其逆定理对比:
勾股定理 勾股定理的逆定理
图形
条件
结论
区别
联系 A
b
a
C
B
∟
在Rt△ABC中,∠C=90°
a2 + b2 = c2
“直角三角形”为条件,数量关系a2 + b2 = c2为结论. 是直角三角形的性质.
A
b
a
C
B
c
都与直角三角形有关,都与三边数量关系a2 + b2 = c2有关
在△ABC中,a2 + b2 = c2
∠C=90°
数量关系a2 + b2 = c2为条件,“直角三角形”为结论. 是直角三角形的判定.
形
数
典例精析
(1) a=8,b=15,c=17;
(2) a=13,b=14,c=15.
【例1】下面以a、b、c为边长的三角形是不是直角三角形?若是,请指出哪个角是直角.
解:(1) ∵82+152=64+225=289,172=289,
∴ 82+152=172.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
(2) ∵132+142=365,152=225,
∴ 132+142≠152,不符合勾股定理的逆定理,
∴ 这个三角形不是直角三角形.
【例2】已知△ABC,AB=n2-1,BC=2n,AC=n2+1(n为大于1的正整数).试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由.
解:∵AB2+BC2=(n2-1)2+(2n)2
=n4-2n2+1+4n4
=n4+2n2+1
=(n2+1)2
=AC2,
∴△ABC是直角三角形,边AC所对的角是直角.
想一想,为什么选择AB2+BC2?AB、BC、CA的大小关系是怎样的?
练一练
(1) a=7,b=25,c=24;
1、判断由a、b、c组成的三角形是不是直角三角形,若是,请指出哪个角是直角.
(2) a:b:c=3:4:5.
解:(1) ∵72+242=49+576=625,252=625,
∴ 72+242=252.
∴根据勾股定理的逆定理得这个三角形是直角三角形,∠B是直角.
(2)设a=3k、b=4k、c=5k,
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
根据勾股定理的逆定理得这个三角形是直角三角形,∠C是直角.
2、一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,你说这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
知识点二 常见的勾股数
满足a2+b2=c2的三个正整数, 称为勾股数。
常见的基本勾股数有:
3,4,5;
6,8,10;
5,12,13;
8,15,17;
7,24,25;
9,40,41;
1.“勾股数”的任意正整数倍仍是勾股数。
2.判断勾股数的方法:
(1)确定是不是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的平方.
3.易错警示:勾股数必须同时满足两个条件:
(1)三个数都是正整数;
(2)两个较小数的平方和等于最大数的平方.
典例精析
【例3】 下列各组数是勾股数的是( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132
A
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
练一练
1、像(3,4,5)、(6,8,10)、(5,12,13)等满足a2+b2=c2的三个正整数,通常称为勾股数,请你填表并探索规律.
a 3 6 9 12 … 3n
b 4 8 12 16 … 4n
c 5 10 15 20 … 5n
a 3 5 7 9 11 … 2n+1
b 4 12 24 40 60 … 2n(n+1)
c 5 13 25 41 61 … 2n(n+1)+1
①从上面2个表中你能发现什么规律?
②你能根据发现的规律写出更多的勾股数吗?试试看 .
解:①规律:一组勾股数,都扩大相同倍数n(n为正整数),得到一组新数,这组数同样是勾股数.
勾股数的性质
②答案不唯一,如:15,20,25;13,84,85等.
利用勾股数可以构造直角三角形.
1.设三角形的三边长分别等于下列各组数,试判断各三角形是否是直角三角形.若是,指出哪一条边所对的角是直角.
(1) 12,16,20; (2) 1.5,2,2.5.
解:(1)因为122+162=400=202,所以是直角三角形,且边长为20的边所对的角为直角.
(2)因为1.52+22=2.52,所以是直角三角形,且边长为2.5的边所对的角为直角.
2.若一个三角形的三条边长a、b、c满足a2=c2-b2,则这个三角形是直角三角形吗?
解:因为a2=c2-b2,所以a2+b2=c2,所以这个三角形是直角三角形.
3.以下各组数为边长,能组成直角三角形的是( ).
A.5,6,7 B.10,8,4
C.7,25,24 D.9,17,15
4.以下各组正数为边长,能组成直角三角形的是( ).
A. B.
C. D.
C
B
1. 四根小棒的长分别是5,9,12,13,从
中任意选择三根小棒首尾相接,搭成边长如下的四个三角形,
其中是直角三角形的是( )
C
A. 5,9,12 B. 5,9,13
C. 5,12,13 D. 9,12,13
2. 若三角形的三边长分别为,, ,且满足
,则此三角形中最大的角是( )
B
A. 锐角 B. 直角 C. 钝角 D. 无法确定
返回
3. 如图,有四个三角形,各有一边长为6,一边长为8,若第
三边长分别为6,8,10,12,则面积最大的三角形是( )
C
A. B. C. D.
返回
(第4题)
4. [2025西安雁塔区月考]如图,在
由小正方形组成的 网格中,每个
小正方形的顶点称为格点.点, ,
,,,均在格点上,点, ,
,中能与点, 构成一个直角三角
形的是( )
D
A. 点 B. 点 C. 点 D. 点
返回
(第5题)
5.如图,在四边形 中,
, , ,
,则 的度数为______.
【点拨】连结, ,
,
是等边三角形,
, . ,
,
,
, .
(第5题)
返回
6.[2025徐州期中]如图,把一块 土地划出一个
后,测得米,米, 米,
米,其中 .
(1)判断 的形状,并说明理由;
【解】 是直角三角形.
理由: , 米,
米,
(米).
又米,米, ,
是直角三角形, .
(2)求图中阴影部分的面积.
阴影部分的面积
(平方米).
返回
7. [2025常州期末]下列由三条线段,,构成的三角形
其内角分别为,,:; ,
,; ;
,,为大于1的整数 ,其
中能构成直角三角形的是( )
B
A. ①④ B. ①②④ C. ②③④ D. ①②③
【点拨】, ,
, , 能构成直角三角形;
, ,
, 能构成直角三角形;
, ,
, 不能构成直角三角形;
, ,
, 能构成直角三角形. 能构成直角三角形
的是①②④.
已知三角形三边的长,常常借助勾股定理的逆定理
来探究三角形是不是直角三角形.在利用公式 时
一定要注意是最大边,即 .
返回
8.如图,在正方形网格中,每个小正方形
的边长都是1个单位长度,点,, ,
,均在小正方形的顶点上,线段 ,
交于点,若 ,则 等
于________.(结果用含 的式子表示)
直角三角形的判定
勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形
勾股数:满足a2+b2=c2的三个正整数
谢谢观看!
