13.2勾股定理的应用 课件(共35张PPT)
文档属性
| 名称 | 13.2勾股定理的应用 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:57:50 | ||
图片预览







文档简介
(共35张PPT)
13.2勾股定理的应用
第13章 勾股定理
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
勾股定理的应用教案
一、教学目标
(一)知识与技能目标
学生能熟练运用勾股定理解决实际生活中的问题,如测量距离、计算高度等,准确识别问题中的直角三角形模型。
掌握勾股定理在几何图形计算中的应用,包括求解三角形边长、判断三角形形状,以及在四边形、圆等图形与直角三角形结合问题中的运用。
学会运用勾股定理的逆定理判断一个三角形是否为直角三角形,并能灵活运用正、逆定理解决综合性问题。
(二)过程与方法目标
通过分析实际问题和几何图形,培养学生将实际问题转化为数学问题的能力,以及从复杂图形中抽象出直角三角形模型的能力。
在解决问题的过程中,提高学生运用数学知识进行逻辑推理和计算的能力,增强学生分析问题、解决问题的思维能力。
(三)情感态度与价值观目标
让学生体会勾股定理在实际生活和数学研究中的广泛应用,激发学生学习数学的兴趣和热情。
通过解决实际问题,培养学生的应用意识和创新精神,增强学生对数学价值的认识,提高学生学习数学的自信心。
二、教学重难点
(一)教学重点
勾股定理在实际生活中的应用,如测量、建筑、航行等问题的解决。
勾股定理及其逆定理在几何图形计算和证明中的综合运用。
(二)教学难点
如何从实际问题中抽象出直角三角形模型,准确找出问题中的已知条件和所求量。
勾股定理与其他数学知识(如方程、函数、几何图形性质等)的综合应用,以及在复杂几何图形中灵活运用勾股定理解决问题。
三、教学方法
讲授法、案例教学法、小组合作探究法、问题驱动法相结合
四、教学过程
(一)复习导入(5 分钟)
知识回顾:提问学生勾股定理的内容(直角三角形两直角边的平方和等于斜边的平方,即\(a^2 + b^2 = c^2\),其中\(a\)、\(b\)为直角边,\(c\)为斜边)及其逆定理(若三角形三边\(a\)、\(b\)、\(c\)满足\(a^2 + b^2 = c^2\),则该三角形为直角三角形),并让学生举例说明。
情境引入:展示一些生活中与勾股定理应用相关的图片或视频,如斜拉桥的结构、测量树高、梯子滑动问题等,提出问题 “在这些情境中,我们如何运用勾股定理来解决问题呢?”,从而引出本节课的主题 —— 勾股定理的应用。
(二)勾股定理在实际生活中的应用讲解(15 分钟)
案例 1:测量问题(5 分钟)
呈现问题:如图,有一个水池,水面是一个边长为\(10\)尺的正方形,在水池正中央有一根芦苇,它高出水面\(1\)尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?
分析问题:引导学生将实际问题转化为数学问题,构建直角三角形模型。设水的深度为\(x\)尺,则芦苇的长度为\((x + 1)\)尺,根据勾股定理列出方程\(x^2 + (\frac{10}{2})^2 = (x + 1)^2\)。
求解问题:教师带领学生解方程,得出\(x = 12\),进而得到芦苇的长度为\(13\)尺。
总结方法:强调在解决测量问题时,要善于找出直角三角形,确定三边关系,通过设未知数,利用勾股定理列方程求解。
案例 2:建筑与工程问题(5 分钟)
呈现问题:某工程队要从 A 点出发到位于马路对面的 B 点进行工程施工,已知马路宽\(12\)米,A、B 两点在马路方向上的水平距离为\(5\)米,为了节省材料,工程队需要铺设的最短管道长度是多少米?
分析问题:引导学生将马路和管道抽象为直角三角形的两条直角边和斜边,运用勾股定理计算斜边长度,即最短管道长度为\(\sqrt{12^2 + 5^2} = 13\)米。
拓展思考:提出问题 “如果马路中间有障碍物,不能直接铺设,该如何设计管道路线?”,激发学生进一步思考。
案例 3:航行问题(5 分钟)
呈现问题:一艘轮船以\(16\)海里 / 小时的速度离开港口向东南方向航行,另一艘轮船在同时同地以\(12\)海里 / 小时的速度向西南方向航行,它们离开港口一个半小时后相距多远?
分析问题:根据方向可知两艘轮船的行驶路线夹角为\(90^{\circ}\),分别计算出两艘轮船行驶的路程作为直角三角形的两条直角边,再利用勾股定理求出斜边,即相距距离为\(\sqrt{(16 1.5)^2 + (12 1.5)^2} = 30\)海里。
总结归纳:总结航行问题中运用勾股定理的关键是确定直角三角形的三边,通常根据行驶方向和速度求出直角边长度。
(三)勾股定理在几何图形中的应用讲解(15 分钟)
在三角形中的应用(5 分钟)
例 1:已知直角三角形的两条直角边分别为\(3\)和\(4\),求斜边的长度;若已知斜边为\(5\),一条直角边为\(3\),求另一条直角边的长度。
分析与解答:直接运用勾股定理\(a^2 + b^2 = c^2\)及其变形公式进行计算,让学生熟练掌握勾股定理在直角三角形边长计算中的应用。
例 2:判断以线段\(a = 5\),\(b = 12\),\(c = 13\)为边的三角形是否为直角三角形。
分析与解答:运用勾股定理逆定理,计算\(a^2 + b^2 = 5^2 + 12^2 = 169 = 13^2 = c^2\),得出该三角形是直角三角形,强化学生对逆定理的应用。
在四边形中的应用(5 分钟)
例 3:如图,在四边形\(ABCD\)中,\(AB = 3\),\(BC = 4\),\(CD = 12\),\(DA = 13\),且\(\angle B = 90^{\circ}\),求四边形\(ABCD\)的面积。
分析与解答:连接\(AC\),在\(Rt\triangle ABC\)中,根据勾股定理求出\(AC = 5\);再在\(\triangle ACD\)中,通过计算\(AC^2 + CD^2 = 5^2 + 12^2 = 169 = 13^2 = AD^2\),由勾股定理逆定理判断\(\triangle ACD\)是直角三角形;最后将四边形面积转化为两个直角三角形面积之和,即\(S_{ è ABCD} = S_{\triangle ABC} + S_{\triangle ACD} = \frac{1}{2} 3 4 + \frac{1}{2} 5 12 = 36\)。
总结方法:在四边形问题中,常常通过作辅助线构造直角三角形,利用勾股定理及其逆定理求解边长和面积。
与圆结合的应用(5 分钟)
例 4:如图,在以\(O\)为圆心的圆中,弦\(AB = 8\),圆心\(O\)到弦\(AB\)的距离\(OC = 3\),求圆的半径\(OA\)。
分析与解答:因为\(OC\)垂直平分\(AB\),所以\(AC = \frac{1}{2}AB = 4\),在\(Rt\triangle AOC\)中,根据勾股定理可得\(OA = \sqrt{AC^2 + OC^2} = \sqrt{4^2 + 3^2} = 5\)。
拓展延伸:引导学生思考在圆中涉及弦长、半径、弦心距等问题时,如何利用勾股定理建立它们之间的关系。
(四)课堂练习(10 分钟)
基础练习:
一个直角三角形的斜边为\(10\),一条直角边为\(6\),求另一条直角边的长度。
如图,一个梯子\(AB\)长\(2.5\)米,顶端\(A\)靠在墙\(AC\)上,这时梯子下端\(B\)与墙角\(C\)距离为\(1.5\)米,梯子滑动后停在\(DE\)的位置上,测得\(BD\)长为\(0.5\)米,求梯子顶端\(A\)下落了多少米?
提高练习:
已知三角形三边分别为\(a\)、\(b\)、\(c\),且\(a^2 + b^2 + c^2 = 10a + 24b + 26c - 338\),试判断该三角形的形状。
在\(\triangle ABC\)中,\(AB = 15\),\(AC = 13\),高\(AD = 12\),求\(\triangle ABC\)的面积。
学生独立完成练习,教师巡视指导,及时发现学生存在的问题,对有困难的学生进行个别辅导。选取部分学生的解答进行展示,组织学生进行讨论和评价,共同纠正错误,总结解题方法和技巧。
(五)课堂小结(5 分钟)
知识梳理:通过提问和总结的方式,引导学生回顾勾股定理在实际生活和几何图形中的应用类型,如测量问题、建筑问题、三角形和四边形计算问题等,以及运用勾股定理及其逆定理解决问题的方法和步骤。
方法归纳:强调在应用勾股定理时,关键是找出或构造直角三角形,确定三边关系;对于实际问题,要善于将其转化为数学模型;对于几何图形问题,要结合图形性质灵活运用定理。同时,鼓励学生在今后的学习和生活中,主动运用勾股定理解决遇到的问题。
(六)作业布置(1 分钟)
必做题:课本习题 [具体页码] 第 [X]、[X]、[X] 题,要求认真分析题目,规范书写解题过程。
选做题:查阅资料,了解勾股定理在古代数学和现代科技中的更多应用实例,并写一篇关于勾股定理应用的小报告;尝试设计一个利用勾股定理解决实际问题的方案,如测量学校旗杆的高度等。
此教案从多场景展现勾股定理应用。你可对案例类型、练习数量等方面提出意见,我会进一步完善教案内容。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、能运用勾股定理及其逆定理解决简单的实际问题;
2、经历勾股定理的应用过程,熟练掌握其应用方法,明确应用条件;
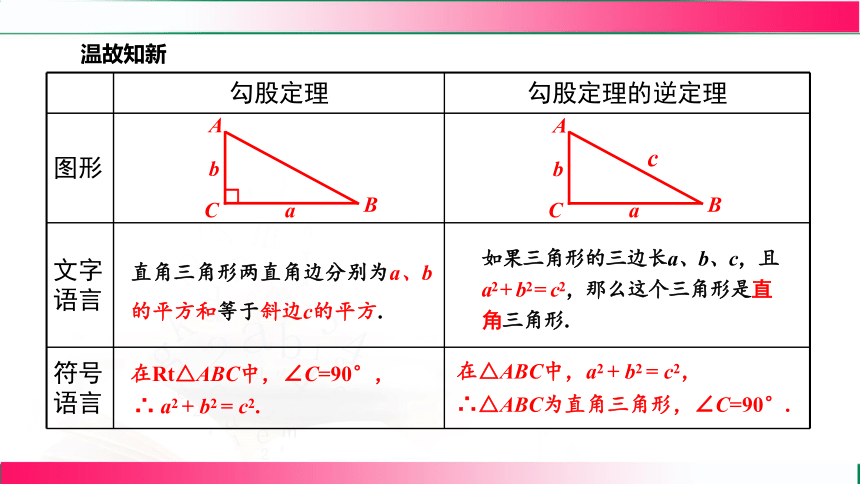
温故知新
勾股定理 勾股定理的逆定理
图形
文字语言
符号语言
A
b
a
C
B
∟
在Rt△ABC中,∠C=90°,
∴ a2 + b2 = c2.
A
b
a
C
B
c
在△ABC中,a2 + b2 = c2,
∴△ABC为直角三角形,∠C=90°.
如果三角形的三边长a、b、c,且a2 + b2 = c2,那么这个三角形是直角三角形.
直角三角形两直角边分别为a、b的平方和等于斜边c的平方.
从远处看斜拉桥,可以发现有许多直角三角形.
已知桥面上以上的索塔AB的高,怎样计算拉索AC、AD、AE、AF、AG的长?
分别测量出BC、BD、BE、BF、BG的长度,根据勾股定理计算出AC、AD、AE、AF、AG的长
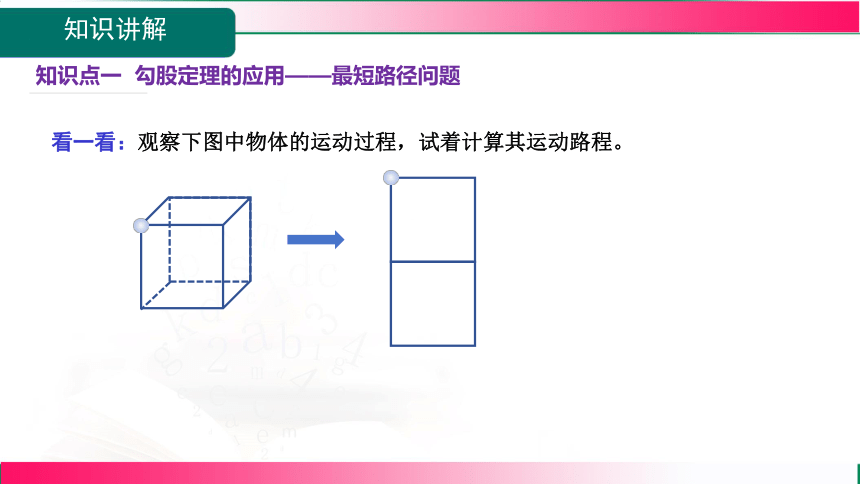
知识点一 勾股定理的应用——最短路径问题
看一看:观察下图中物体的运动过程,试着计算其运动路程。
典例精析
【例1】如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
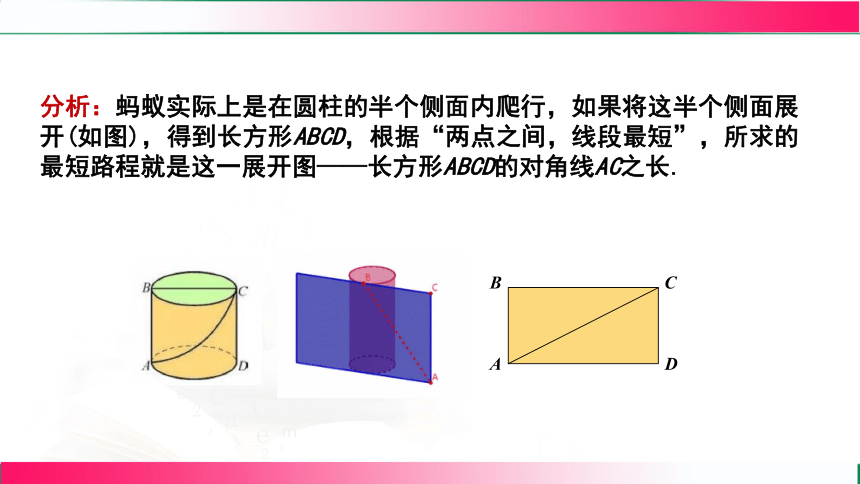
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图),得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
A
B
C
D
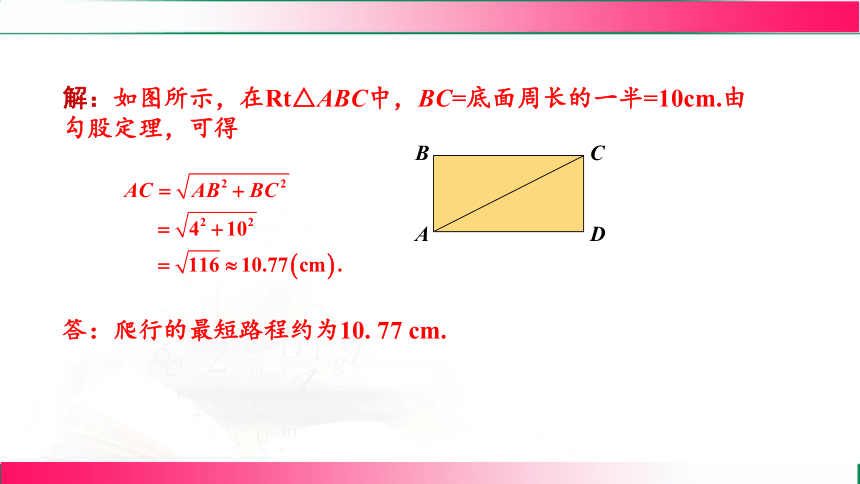
解:如图所示,在Rt△ABC中,BC=底面周长的一半=10cm.由勾股定理,可得
A
B
C
D
答:爬行的最短路程约为10. 77 cm.
练一练
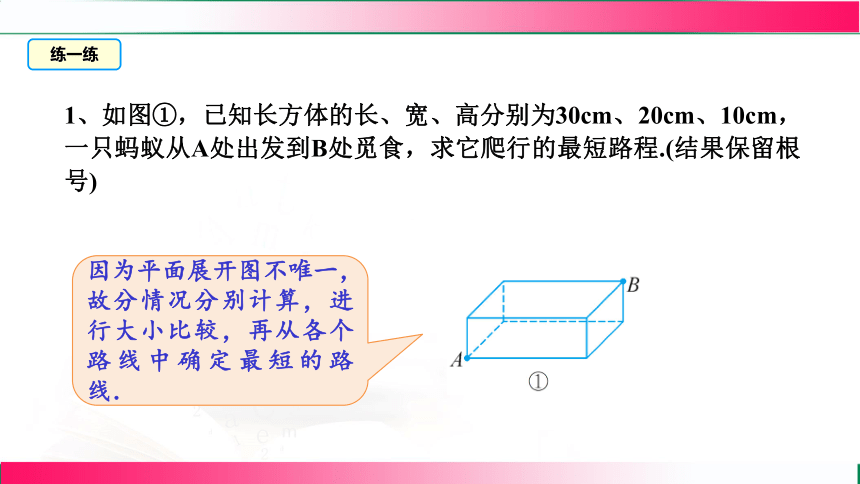
1、如图①,已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它爬行的最短路程.(结果保留根号)
因为平面展开图不唯一,故分情况分别计算,进行大小比较,再从各个路线中确定最短的路线.
解:长方体的展开图如图
如图②,展开前面、右面,由勾股定理得AB=
=
如图③,展开前面、上面,由勾股定理得AB=
=
如图④,展开左面、上面,由勾股定理得AB=
=
∵ ,∴爬行最短路程为 cm.
知识点二 勾股定理的应用——几何问题
【例2】 如图, 在△ABC中, AB=26, BC=20, BC边上的中线AD=24, 求AC.
D
C
B
A
26
20
24
解:∵AD是△ABC的中线,且BC=20,
∴BD==10.
∵AD2+BD2=576+100=676,
AB 2=262=676,
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
还有其他方法求AC吗?
能求出△ABC的周长和面积吗
典例精析
练一练
1. 计算图中四边形ABCD的面积.
解:在Rt△ADB中,由勾股定理得:
BD2=AD2+AB2=122+162=400 ,
∴BD=20,
∵CD2=152=225,
∴ CD2+BD2=BC2.
∴ 由勾股定理的逆定理得:∠BDC=90°.
∴ BD⊥CD
S四边形ABCD=S△ABD+S△BDC
=×16×12+×15×20=246.
D
C
B
A
∟
12
16
15
25
BC2=252=625,
2. 一个三角形三边长的比为3:4:5,它的周长是60cm. 求这个三角形的面积.
解:∵三边长的比为3:4:5,它的周长是60cm.
∴三边长分别为:
60×,60×,60×,
∵152+202=252,
∴这个三角形是直角三角形,
∴这个三角形的面积是:
.
知识点三 勾股定理的实际应用
典例精析
【例3】如图,四边形ABCD是学校的一块空地,经数学兴趣小组的测量可知,∠B=90°,BC=3米,AB=4米,CD=13米,AD=12米.为了提高校园的绿化面积,现学校决定在空地内铺草坪,若铺设每平方米草坪需要30元,则将这块空地全部铺满一层草坪的费用是多少?
A
B
C
D
3
4
12
13
解:如图,连接AC.在Rt△ABC中,由勾股定理得:
AC2=AB2+BC2=32+42,∴AC=5.∵AC2+AD2=52+122=169,CD2=169,∴CD2=AC2+AD2.∴由勾股定理的逆定理得:∠CAD=90°.∴S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·AD=×4×3+×5×12=36.
∵36×30=1080(元),
∴这块地全部种草的费用是1080元.
∟
练一练
1、一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
分析:由于车宽1.6米,所以卡车能否通过,只要比较距厂门中线0.8米处的高度与车高即可.如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面相交于点H.
解:在Rt△OCD中,由勾股定理,可得
CH=CD+DH=0.6+2.3=2.9>2.5.
可见高度上有0.4米的余量,因此卡车能通过厂门.
2、有一根高为16米的电线杆在A处断裂,如图所示,电线杆的顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到地面的距离.
根据题意可知在Rt△ABC中,∠ABC =90°,BC=8米,AB+AC=16米.若设AB=x米,则AC=(16-x)米,然后根据勾股定理列出方程求解.
解:在Rt△ABC中,∠ABC=90°.
设AB=x米,则AC=(16-x)米.
根据勾股定理,得x2+82=(16-x)2,
解得x=6,即AB=6米.
答:电线杆断裂处A到地面的距离为6米.
1.如图,将一根长13厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为( )厘米.
A.1 B.2 C.3 D.4
C
13cm
8cm
6cm
?cm
2.如图,由于台风影响,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是 米.
8
3、在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+x2=(x+1)2
25+x2= x2+2x+1,
2x=24,
∴ x=12, x+1=13 .
答:水池的水深12尺,这根芦苇长13尺.
解:
4.如图,已知CD=6cm,AD=8cm, ∠ADC=90o,BC=24cm,AB=26cm,求阴影部分面积.
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD
=120-24
=96.
1. 如图,长为的橡皮筋放置在直线上,固定两端点
和,然后把中点向上拉升至 点,则橡皮筋被拉长了
( )
(第1题)
A. B. C. D.
√
返回
(第2题)
2. 如图,一圆柱体
的底面周长为,高为, 是
直径,一只蚂蚁从点 出发沿着圆柱体的侧
面爬行到点 的最短路程是( )
A. B. C. D.
√
返回
(第3题)
3.[2025洛阳期末]如图,在离水面
高度为8米的岸上,有人用绳子拉船
靠岸,开始时绳子 的长为17米,
几分钟后船到达点 的位置,此时绳
子 的长为10米,则船向岸边移动
了___米.
9
(第3题)
【点拨】 在 中,
,米,
(米), 船向岸边移动了9米.
米,
(米) 米,
(米),
返回
(第4题)
4. 如图,在笔直的铁路
上有两点,,相距,, 为
两村庄,, ,
于点,于点 ,现要
在上建一个中转站,使得, 两
13.3
村庄到站的距离相等,则_____ .
返回
5.《国务院关于印发全民健身计划
(2021-2025年)的通知》文件提出,加大
全民健身场地设施供给,进一步增加全民
健身的热情.某市某健身广场为方便群众夜
间健身活动,在广场部分位置加装照明灯,
向阳兴趣小组利用长的竹竿测量照明灯灯板 的长.如
图,灯板垂直地面于点 ,第一次将竹竿的一个端点
与点重合,另一个端点落在地面上的 处,
第二次将竹竿的一个端点与点 重合,另一
个端点落在地面上的处.已知 ,
,求灯板 的长.
【解】由题意可知, .在
中,, ,则
.
在中,, ,
则 .
.
返回
6.在底面周长约为6米且带有层层回环不断的云朵石柱上,有
一条雕龙从柱底沿石柱表面均匀地盘绕2圈到达柱顶正上方,
石柱上刻有雕龙的部分的柱高约为16米,则雕刻在石柱上的
巨龙至少长为______.
20米
返回
7. 跷跷板是一种常见的儿童玩具.跷跷板一端
着地时如图①,支柱 地面,, 为握把,
且于,, .跷跷板可以绕点
转动,如图②是跷跷板水平时,即,此时点 ,
,,的对应点分别为点,,,,恰有 .则
跷跷板的长为_____ .
265
勾股定理的应用
最短路径问题
求最短路径长度
实际问题中的应用
求长度、距离、宽度、高度等
关键:构造直角三角形
几何问题中的应用
求三角形的边长、求图形的面积等
谢谢观看!
13.2勾股定理的应用
第13章 勾股定理
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
勾股定理的应用教案
一、教学目标
(一)知识与技能目标
学生能熟练运用勾股定理解决实际生活中的问题,如测量距离、计算高度等,准确识别问题中的直角三角形模型。
掌握勾股定理在几何图形计算中的应用,包括求解三角形边长、判断三角形形状,以及在四边形、圆等图形与直角三角形结合问题中的运用。
学会运用勾股定理的逆定理判断一个三角形是否为直角三角形,并能灵活运用正、逆定理解决综合性问题。
(二)过程与方法目标
通过分析实际问题和几何图形,培养学生将实际问题转化为数学问题的能力,以及从复杂图形中抽象出直角三角形模型的能力。
在解决问题的过程中,提高学生运用数学知识进行逻辑推理和计算的能力,增强学生分析问题、解决问题的思维能力。
(三)情感态度与价值观目标
让学生体会勾股定理在实际生活和数学研究中的广泛应用,激发学生学习数学的兴趣和热情。
通过解决实际问题,培养学生的应用意识和创新精神,增强学生对数学价值的认识,提高学生学习数学的自信心。
二、教学重难点
(一)教学重点
勾股定理在实际生活中的应用,如测量、建筑、航行等问题的解决。
勾股定理及其逆定理在几何图形计算和证明中的综合运用。
(二)教学难点
如何从实际问题中抽象出直角三角形模型,准确找出问题中的已知条件和所求量。
勾股定理与其他数学知识(如方程、函数、几何图形性质等)的综合应用,以及在复杂几何图形中灵活运用勾股定理解决问题。
三、教学方法
讲授法、案例教学法、小组合作探究法、问题驱动法相结合
四、教学过程
(一)复习导入(5 分钟)
知识回顾:提问学生勾股定理的内容(直角三角形两直角边的平方和等于斜边的平方,即\(a^2 + b^2 = c^2\),其中\(a\)、\(b\)为直角边,\(c\)为斜边)及其逆定理(若三角形三边\(a\)、\(b\)、\(c\)满足\(a^2 + b^2 = c^2\),则该三角形为直角三角形),并让学生举例说明。
情境引入:展示一些生活中与勾股定理应用相关的图片或视频,如斜拉桥的结构、测量树高、梯子滑动问题等,提出问题 “在这些情境中,我们如何运用勾股定理来解决问题呢?”,从而引出本节课的主题 —— 勾股定理的应用。
(二)勾股定理在实际生活中的应用讲解(15 分钟)
案例 1:测量问题(5 分钟)
呈现问题:如图,有一个水池,水面是一个边长为\(10\)尺的正方形,在水池正中央有一根芦苇,它高出水面\(1\)尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?
分析问题:引导学生将实际问题转化为数学问题,构建直角三角形模型。设水的深度为\(x\)尺,则芦苇的长度为\((x + 1)\)尺,根据勾股定理列出方程\(x^2 + (\frac{10}{2})^2 = (x + 1)^2\)。
求解问题:教师带领学生解方程,得出\(x = 12\),进而得到芦苇的长度为\(13\)尺。
总结方法:强调在解决测量问题时,要善于找出直角三角形,确定三边关系,通过设未知数,利用勾股定理列方程求解。
案例 2:建筑与工程问题(5 分钟)
呈现问题:某工程队要从 A 点出发到位于马路对面的 B 点进行工程施工,已知马路宽\(12\)米,A、B 两点在马路方向上的水平距离为\(5\)米,为了节省材料,工程队需要铺设的最短管道长度是多少米?
分析问题:引导学生将马路和管道抽象为直角三角形的两条直角边和斜边,运用勾股定理计算斜边长度,即最短管道长度为\(\sqrt{12^2 + 5^2} = 13\)米。
拓展思考:提出问题 “如果马路中间有障碍物,不能直接铺设,该如何设计管道路线?”,激发学生进一步思考。
案例 3:航行问题(5 分钟)
呈现问题:一艘轮船以\(16\)海里 / 小时的速度离开港口向东南方向航行,另一艘轮船在同时同地以\(12\)海里 / 小时的速度向西南方向航行,它们离开港口一个半小时后相距多远?
分析问题:根据方向可知两艘轮船的行驶路线夹角为\(90^{\circ}\),分别计算出两艘轮船行驶的路程作为直角三角形的两条直角边,再利用勾股定理求出斜边,即相距距离为\(\sqrt{(16 1.5)^2 + (12 1.5)^2} = 30\)海里。
总结归纳:总结航行问题中运用勾股定理的关键是确定直角三角形的三边,通常根据行驶方向和速度求出直角边长度。
(三)勾股定理在几何图形中的应用讲解(15 分钟)
在三角形中的应用(5 分钟)
例 1:已知直角三角形的两条直角边分别为\(3\)和\(4\),求斜边的长度;若已知斜边为\(5\),一条直角边为\(3\),求另一条直角边的长度。
分析与解答:直接运用勾股定理\(a^2 + b^2 = c^2\)及其变形公式进行计算,让学生熟练掌握勾股定理在直角三角形边长计算中的应用。
例 2:判断以线段\(a = 5\),\(b = 12\),\(c = 13\)为边的三角形是否为直角三角形。
分析与解答:运用勾股定理逆定理,计算\(a^2 + b^2 = 5^2 + 12^2 = 169 = 13^2 = c^2\),得出该三角形是直角三角形,强化学生对逆定理的应用。
在四边形中的应用(5 分钟)
例 3:如图,在四边形\(ABCD\)中,\(AB = 3\),\(BC = 4\),\(CD = 12\),\(DA = 13\),且\(\angle B = 90^{\circ}\),求四边形\(ABCD\)的面积。
分析与解答:连接\(AC\),在\(Rt\triangle ABC\)中,根据勾股定理求出\(AC = 5\);再在\(\triangle ACD\)中,通过计算\(AC^2 + CD^2 = 5^2 + 12^2 = 169 = 13^2 = AD^2\),由勾股定理逆定理判断\(\triangle ACD\)是直角三角形;最后将四边形面积转化为两个直角三角形面积之和,即\(S_{ è ABCD} = S_{\triangle ABC} + S_{\triangle ACD} = \frac{1}{2} 3 4 + \frac{1}{2} 5 12 = 36\)。
总结方法:在四边形问题中,常常通过作辅助线构造直角三角形,利用勾股定理及其逆定理求解边长和面积。
与圆结合的应用(5 分钟)
例 4:如图,在以\(O\)为圆心的圆中,弦\(AB = 8\),圆心\(O\)到弦\(AB\)的距离\(OC = 3\),求圆的半径\(OA\)。
分析与解答:因为\(OC\)垂直平分\(AB\),所以\(AC = \frac{1}{2}AB = 4\),在\(Rt\triangle AOC\)中,根据勾股定理可得\(OA = \sqrt{AC^2 + OC^2} = \sqrt{4^2 + 3^2} = 5\)。
拓展延伸:引导学生思考在圆中涉及弦长、半径、弦心距等问题时,如何利用勾股定理建立它们之间的关系。
(四)课堂练习(10 分钟)
基础练习:
一个直角三角形的斜边为\(10\),一条直角边为\(6\),求另一条直角边的长度。
如图,一个梯子\(AB\)长\(2.5\)米,顶端\(A\)靠在墙\(AC\)上,这时梯子下端\(B\)与墙角\(C\)距离为\(1.5\)米,梯子滑动后停在\(DE\)的位置上,测得\(BD\)长为\(0.5\)米,求梯子顶端\(A\)下落了多少米?
提高练习:
已知三角形三边分别为\(a\)、\(b\)、\(c\),且\(a^2 + b^2 + c^2 = 10a + 24b + 26c - 338\),试判断该三角形的形状。
在\(\triangle ABC\)中,\(AB = 15\),\(AC = 13\),高\(AD = 12\),求\(\triangle ABC\)的面积。
学生独立完成练习,教师巡视指导,及时发现学生存在的问题,对有困难的学生进行个别辅导。选取部分学生的解答进行展示,组织学生进行讨论和评价,共同纠正错误,总结解题方法和技巧。
(五)课堂小结(5 分钟)
知识梳理:通过提问和总结的方式,引导学生回顾勾股定理在实际生活和几何图形中的应用类型,如测量问题、建筑问题、三角形和四边形计算问题等,以及运用勾股定理及其逆定理解决问题的方法和步骤。
方法归纳:强调在应用勾股定理时,关键是找出或构造直角三角形,确定三边关系;对于实际问题,要善于将其转化为数学模型;对于几何图形问题,要结合图形性质灵活运用定理。同时,鼓励学生在今后的学习和生活中,主动运用勾股定理解决遇到的问题。
(六)作业布置(1 分钟)
必做题:课本习题 [具体页码] 第 [X]、[X]、[X] 题,要求认真分析题目,规范书写解题过程。
选做题:查阅资料,了解勾股定理在古代数学和现代科技中的更多应用实例,并写一篇关于勾股定理应用的小报告;尝试设计一个利用勾股定理解决实际问题的方案,如测量学校旗杆的高度等。
此教案从多场景展现勾股定理应用。你可对案例类型、练习数量等方面提出意见,我会进一步完善教案内容。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1、能运用勾股定理及其逆定理解决简单的实际问题;
2、经历勾股定理的应用过程,熟练掌握其应用方法,明确应用条件;
温故知新
勾股定理 勾股定理的逆定理
图形
文字语言
符号语言
A
b
a
C
B
∟
在Rt△ABC中,∠C=90°,
∴ a2 + b2 = c2.
A
b
a
C
B
c
在△ABC中,a2 + b2 = c2,
∴△ABC为直角三角形,∠C=90°.
如果三角形的三边长a、b、c,且a2 + b2 = c2,那么这个三角形是直角三角形.
直角三角形两直角边分别为a、b的平方和等于斜边c的平方.
从远处看斜拉桥,可以发现有许多直角三角形.
已知桥面上以上的索塔AB的高,怎样计算拉索AC、AD、AE、AF、AG的长?
分别测量出BC、BD、BE、BF、BG的长度,根据勾股定理计算出AC、AD、AE、AF、AG的长
知识点一 勾股定理的应用——最短路径问题
看一看:观察下图中物体的运动过程,试着计算其运动路程。
典例精析
【例1】如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程. (精确到0.01cm)
分析:蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图),得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
A
B
C
D
解:如图所示,在Rt△ABC中,BC=底面周长的一半=10cm.由勾股定理,可得
A
B
C
D
答:爬行的最短路程约为10. 77 cm.
练一练
1、如图①,已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它爬行的最短路程.(结果保留根号)
因为平面展开图不唯一,故分情况分别计算,进行大小比较,再从各个路线中确定最短的路线.
解:长方体的展开图如图
如图②,展开前面、右面,由勾股定理得AB=
=
如图③,展开前面、上面,由勾股定理得AB=
=
如图④,展开左面、上面,由勾股定理得AB=
=
∵ ,∴爬行最短路程为 cm.
知识点二 勾股定理的应用——几何问题
【例2】 如图, 在△ABC中, AB=26, BC=20, BC边上的中线AD=24, 求AC.
D
C
B
A
26
20
24
解:∵AD是△ABC的中线,且BC=20,
∴BD==10.
∵AD2+BD2=576+100=676,
AB 2=262=676,
∴AD2+BD2=AB2,
∴ ∠ADB=90°,AD垂直平分BC.
∴AC=AB=26.
还有其他方法求AC吗?
能求出△ABC的周长和面积吗
典例精析
练一练
1. 计算图中四边形ABCD的面积.
解:在Rt△ADB中,由勾股定理得:
BD2=AD2+AB2=122+162=400 ,
∴BD=20,
∵CD2=152=225,
∴ CD2+BD2=BC2.
∴ 由勾股定理的逆定理得:∠BDC=90°.
∴ BD⊥CD
S四边形ABCD=S△ABD+S△BDC
=×16×12+×15×20=246.
D
C
B
A
∟
12
16
15
25
BC2=252=625,
2. 一个三角形三边长的比为3:4:5,它的周长是60cm. 求这个三角形的面积.
解:∵三边长的比为3:4:5,它的周长是60cm.
∴三边长分别为:
60×,60×,60×,
∵152+202=252,
∴这个三角形是直角三角形,
∴这个三角形的面积是:
.
知识点三 勾股定理的实际应用
典例精析
【例3】如图,四边形ABCD是学校的一块空地,经数学兴趣小组的测量可知,∠B=90°,BC=3米,AB=4米,CD=13米,AD=12米.为了提高校园的绿化面积,现学校决定在空地内铺草坪,若铺设每平方米草坪需要30元,则将这块空地全部铺满一层草坪的费用是多少?
A
B
C
D
3
4
12
13
解:如图,连接AC.在Rt△ABC中,由勾股定理得:
AC2=AB2+BC2=32+42,∴AC=5.∵AC2+AD2=52+122=169,CD2=169,∴CD2=AC2+AD2.∴由勾股定理的逆定理得:∠CAD=90°.∴S四边形ABCD=S△ABC+S△ACD=AB·BC+AC·AD=×4×3+×5×12=36.
∵36×30=1080(元),
∴这块地全部种草的费用是1080元.
∟
练一练
1、一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图所示的某工厂,问这辆卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
分析:由于车宽1.6米,所以卡车能否通过,只要比较距厂门中线0.8米处的高度与车高即可.如图所示,点D在离厂门中线0.8米处,且CD⊥AB,与地面相交于点H.
解:在Rt△OCD中,由勾股定理,可得
CH=CD+DH=0.6+2.3=2.9>2.5.
可见高度上有0.4米的余量,因此卡车能通过厂门.
2、有一根高为16米的电线杆在A处断裂,如图所示,电线杆的顶部C落在离电线杆底部B处8米远的地方,求电线杆断裂处A到地面的距离.
根据题意可知在Rt△ABC中,∠ABC =90°,BC=8米,AB+AC=16米.若设AB=x米,则AC=(16-x)米,然后根据勾股定理列出方程求解.
解:在Rt△ABC中,∠ABC=90°.
设AB=x米,则AC=(16-x)米.
根据勾股定理,得x2+82=(16-x)2,
解得x=6,即AB=6米.
答:电线杆断裂处A到地面的距离为6米.
1.如图,将一根长13厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为( )厘米.
A.1 B.2 C.3 D.4
C
13cm
8cm
6cm
?cm
2.如图,由于台风影响,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是 米.
8
3、在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
设水池的水深AC为x尺,则这根芦苇长为AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得:BC2+AC2=AB2
即 52+x2=(x+1)2
25+x2= x2+2x+1,
2x=24,
∴ x=12, x+1=13 .
答:水池的水深12尺,这根芦苇长13尺.
解:
4.如图,已知CD=6cm,AD=8cm, ∠ADC=90o,BC=24cm,AB=26cm,求阴影部分面积.
解:在Rt△ADC中,
∵AC2=AD2+CD2(勾股定理)
=82+62=100,
∴AC=10.
∵AC2+BC2=102+242=676=262,
∴△ACB为直角三角形(勾股定理的逆定理).
∴S阴影部分=S△ACB-S△ACD
=120-24
=96.
1. 如图,长为的橡皮筋放置在直线上,固定两端点
和,然后把中点向上拉升至 点,则橡皮筋被拉长了
( )
(第1题)
A. B. C. D.
√
返回
(第2题)
2. 如图,一圆柱体
的底面周长为,高为, 是
直径,一只蚂蚁从点 出发沿着圆柱体的侧
面爬行到点 的最短路程是( )
A. B. C. D.
√
返回
(第3题)
3.[2025洛阳期末]如图,在离水面
高度为8米的岸上,有人用绳子拉船
靠岸,开始时绳子 的长为17米,
几分钟后船到达点 的位置,此时绳
子 的长为10米,则船向岸边移动
了___米.
9
(第3题)
【点拨】 在 中,
,米,
(米), 船向岸边移动了9米.
米,
(米) 米,
(米),
返回
(第4题)
4. 如图,在笔直的铁路
上有两点,,相距,, 为
两村庄,, ,
于点,于点 ,现要
在上建一个中转站,使得, 两
13.3
村庄到站的距离相等,则_____ .
返回
5.《国务院关于印发全民健身计划
(2021-2025年)的通知》文件提出,加大
全民健身场地设施供给,进一步增加全民
健身的热情.某市某健身广场为方便群众夜
间健身活动,在广场部分位置加装照明灯,
向阳兴趣小组利用长的竹竿测量照明灯灯板 的长.如
图,灯板垂直地面于点 ,第一次将竹竿的一个端点
与点重合,另一个端点落在地面上的 处,
第二次将竹竿的一个端点与点 重合,另一
个端点落在地面上的处.已知 ,
,求灯板 的长.
【解】由题意可知, .在
中,, ,则
.
在中,, ,
则 .
.
返回
6.在底面周长约为6米且带有层层回环不断的云朵石柱上,有
一条雕龙从柱底沿石柱表面均匀地盘绕2圈到达柱顶正上方,
石柱上刻有雕龙的部分的柱高约为16米,则雕刻在石柱上的
巨龙至少长为______.
20米
返回
7. 跷跷板是一种常见的儿童玩具.跷跷板一端
着地时如图①,支柱 地面,, 为握把,
且于,, .跷跷板可以绕点
转动,如图②是跷跷板水平时,即,此时点 ,
,,的对应点分别为点,,,,恰有 .则
跷跷板的长为_____ .
265
勾股定理的应用
最短路径问题
求最短路径长度
实际问题中的应用
求长度、距离、宽度、高度等
关键:构造直角三角形
几何问题中的应用
求三角形的边长、求图形的面积等
谢谢观看!
