第14章 数据的收集与表示 课件(共57张PPT)
文档属性
| 名称 | 第14章 数据的收集与表示 课件(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 16:00:14 | ||
图片预览








文档简介
(共57张PPT)
章末复习
第14章 数据的收集与表示
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
第 14 章 数据的收集与表示章末复习
一、知识框架梳理
(一)数据的收集
收集意义:数据收集是获取信息的基础,为数据分析、决策提供依据,如企业依据消费者数据调整产品策略 ,学校通过学生数据优化教学。
常用方法
问卷调查法:适用于大规模数据收集,需注意问题设计避免引导性和歧义性,包含标题、指导语、问题和答案等结构。
访谈法:利于深入了解对象想法,分个别访谈和集体访谈,需提前准备提纲,营造良好氛围。
观察法:可直接获取行为现象,分参与式和非参与式,要明确观察对象、内容、时间和地点。
实验法:用于研究因果关系,遵循控制变量等原则,设置对照组和实验组。
(二)数据的表示
统计表:以表格形式呈现数据,结构包括标题、标目、数据和表注,能准确有条理地展示数据,便于对比分析。
统计图
条形统计图:用直条长短表示数量,直观反映数量多少,适合比较不同类别数据差异。
折线统计图:通过折线展示数据增减变化,可体现数量多少与变化趋势,常用于展示随时间等连续变量变化的数据。
扇形统计图:用扇形表示各部分占比,清晰呈现部分与总体比例关系,适用于展示份额分布。
象形统计图:利用形象图案表示数据,更直观有趣,常用于低龄受众或简单数据展示 。
二、典型例题解析
(一)数据收集方法的选择与应用
例 1:要了解全校学生对课后服务社团的喜好情况,应采用哪种数据收集方法?
分析:全校学生数量较多,适合采用问卷调查法,可设计包含各类社团选项的问卷,快速收集大量数据。
解答:选择问卷调查法,设计问卷时注意涵盖所有社团类型,问题表述清晰,便于学生作答。
(二)数据表示方法的选择与绘制
例 2:某商场统计了近半年每月的销售额,分别为:1 月 80 万元,2 月 95 万元,3 月 100 万元,4 月 120 万元,5 月 110 万元,6 月 130 万元。请选择合适的统计图表示这些数据,并绘制出来。
分析:数据是随时间变化的销售额,体现的是数据的增减趋势,所以适合用折线统计图。
解答:
绘制横纵轴,横轴表示月份,纵轴表示销售额(单位:万元),标注刻度。
根据数据在对应位置描点,依次连接各点。
标注图表标题 “某商场近半年每月销售额统计图”。
例 3:某班级学生参加兴趣小组的情况如下:绘画组 15 人,书法组 10 人,音乐组 20 人,体育组 25 人。若要清晰展示各小组人数占总人数的比例关系,应选择哪种统计图?并计算各小组人数占比。
分析:需展示各部分在总体中的占比,应选择扇形统计图。先计算总人数,再分别计算各小组人数占比。
解答:
总人数:\(15 + 10 + 20 + 25 = 70\)(人)
绘画组占比:\(15 ·70 100\% 21.4\%\),对应圆心角:\(360 ° 21.4\% 77 °\)
书法组占比:\(10 ·70 100\% 14.3\%\),对应圆心角:\(360 ° 14.3\% 51 °\)
音乐组占比:\(20 ·70 100\% 28.6\%\),对应圆心角:\(360 ° 28.6\% 103 °\)
体育组占比:\(25 ·70 100\% 35.7\%\),对应圆心角:\(360 ° 35.7\% 128 °\)
绘制扇形统计图,标注各小组名称、占比及圆心角。
三、易错点提醒
数据收集
问卷调查设计问题时,避免出现模糊不清、引导性语句,确保数据真实有效。
根据调查对象和目的合理选择收集方法,如小范围深入调查适合访谈法,大规模普适合问卷调查法。
数据表示
制作统计图时,注意刻度均匀,比例恰当,避免因刻度设置不当导致数据展示偏差。
选择统计图类型要准确,如展示数量变化用折线统计图,比较数量多少用条形统计图,体现占比用扇形统计图。
四、综合练习
(一)基础巩固
学校想了解学生对食堂饭菜的满意度,最适合采用( )收集数据。
A. 观察法 B. 访谈法 C. 问卷调查法 D. 实验法
要统计某地区一周的气温变化情况,应绘制( )统计图。
A. 条形 B. 折线 C. 扇形 D. 象形
制作扇形统计图时,某部分占总体的\(30\%\),则该部分对应的圆心角是( )度。
(二)能力提升
某超市统计了四种饮料一个月的销售数量:可乐 120 瓶,雪碧 80 瓶,橙汁 100 瓶,绿茶 150 瓶。
请制作统计表表示这些数据。
选择合适的统计图绘制出来,并分析哪种饮料最受欢迎。
以下是某班级学生某次数学考试的成绩分布:优秀(85 分及以上)12 人,良好(70 - 84 分)20 人,中等(60 - 69 分)15 人,不及格(60 分以下)3 人。制作扇形统计图展示成绩分布情况,并计算各部分圆心角度数。
五、复习建议
对照知识框架,查漏补缺,确保对数据收集与表示的概念、方法清晰掌握。
整理做过的例题和练习题,分析错题原因,针对薄弱环节加强训练,尤其是数据表示方法的选择和统计图绘制。
关注生活中的数据收集与表示案例,尝试用所学知识进行分析和解读,提高知识应用能力。
这份复习资料涵盖知识、例题与练习。你可以说说对内容深度、练习量等方面的看法,若有其他需求,我会进一步优化。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
考点1 普查与抽样调查
1. “谁知盘中餐,粒粒皆辛苦”,学校为杜绝
舌尖上的浪费开展“光盘行动”活动,为了解七年级200名学生
参与此次活动的现状,采用抽样调查的方式来收集数据,则
抽取样本的方式比较合理的是( )
D
A. 选取50名男生 B. 选取一个班的50名学生
C. 选取50名女生 D. 随机选取50名学生
返回
2.下列调查中,适合用普查的是______,适合用抽样调查的
是__________.
①了解全国青少年儿童的睡眠时间;
②了解乘客是否携带危险物品乘坐高铁;
③了解某班学生对“雷锋精神”的知晓率;
④了解某市居民对废电池的处理情况;
⑤了解黄河中某些鱼的数量;
⑥了解市民对某部电影的喜欢程度.
②③
①④⑤⑥
返回
考点2 总体、个体、样本和样本容量
3. 为弘扬中华优秀传统文化,倡导健康生活方式,某中学本
学期开设了校本课程“八段锦”,为了解学生对该课程的满意
度,在全校的1 000名学生中随机抽取了100名学生对该课程
的满意程度打分,下列说法正确的是( )
C
A. 样本容量为1 000
B. 总体是100名学生
C. 样本是抽取的100名学生所打的分数
D. 个体是被抽取的每一名学生
返回
考点3 频数与频率
4. “教育强国”四字的汉语拼音中,字母“ ”出现
的频率是( )
C
A. B. C. D.
5.一次数学测试后,某班80名学生的成绩被分为5组,第一至
第四组的频数分别为8,10,16,14,则第五组的频率是____.
0.4
返回
考点4 频数分布直方图(表)
6.某同学统计了他上周通话次数及每次的通话时间,并列出
如下频数分布表:
通话时间 分钟
通话次数 (频数) 26 14 7 2 1
则通话时间超过6分钟的频率是____.
0.2
返回
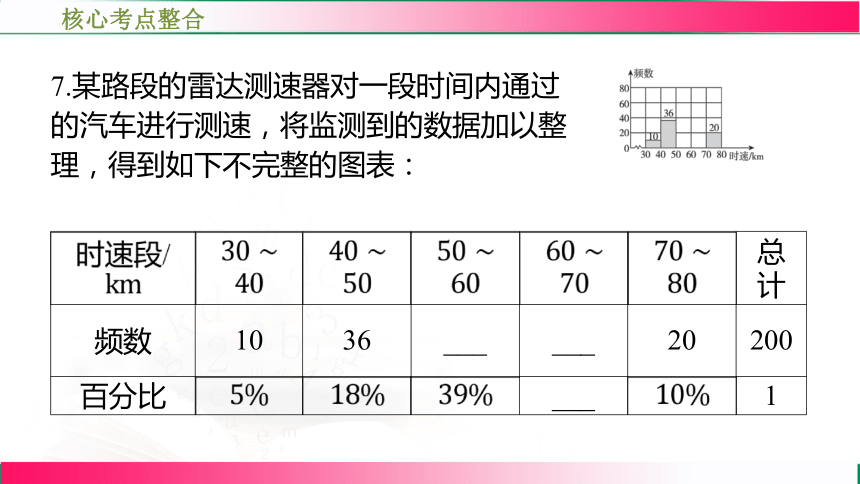
7.某路段的雷达测速器对一段时间内通过
的汽车进行测速,将监测到的数据加以整
理,得到如下不完整的图表:
时速段/ 总
计
频数 10 36 ___ ___ 20 200
百分比 ___ 1
注:“”表示时速大于或等于 且
小于 ,其他类同.
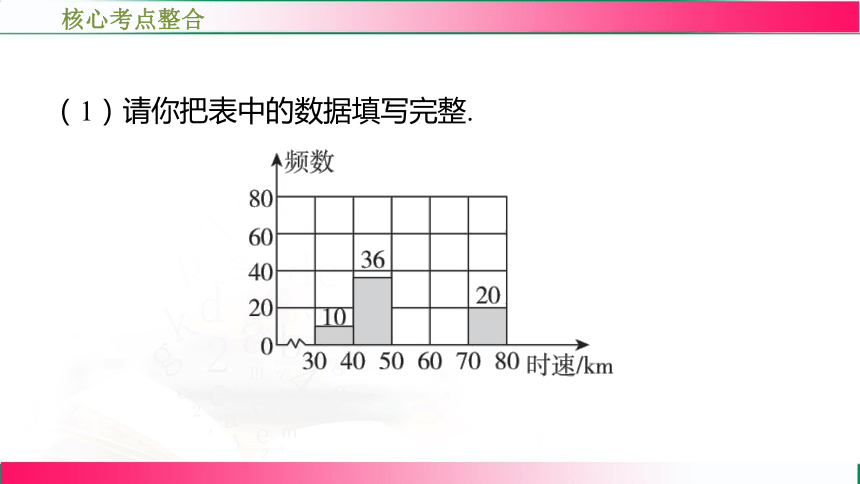
(1)请你把表中的数据填写完整.
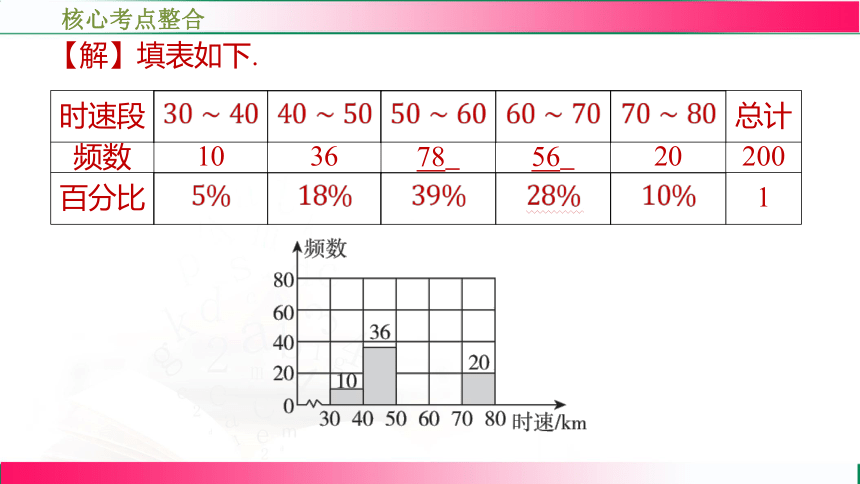
【解】填表如下.
时速段 总计
频数 10 36 78. . 56. . 20 200
百分比 1
. .
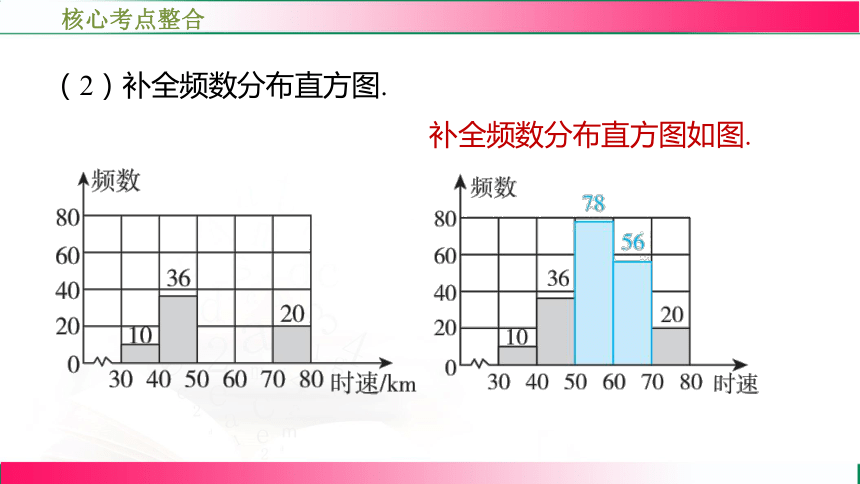
(2)补全频数分布直方图.
补全频数分布直方图如图.
(3)如果此路段汽车时速达
到或超过 即为违章,那
么违章车辆共有多少辆?
(辆).
答:违章车辆共有76辆.
返回
考点5 统计图的应用
8.去年3至8月份期间,,, 三种品牌空调的销售情况如
下列统计图所示,根据统计图,回答下列问题:
(1)3至8月份期间,___品牌空调销售量最多(填“”“ ”或
“”).8月份品牌空调销售量有_____台.扇形统计图中, 品
牌所对应的扇形的圆心角是_____度.
275
97.2
(2)8月份其他品牌的空调销
售总量是多少台?
【解】8月份空调销售总量为
(台),
月份其他品牌的空调销售
总量是221台.
(台),
返回
思想1 数形结合思想
9.某校进行了“交通法规要牢记,路过
街市别大意”交通安全知识竞赛,为了
解本校学生对交通安全知识的掌握情
况,随机抽取了部分学生的成绩
(单位:分),并将他们的成绩整理
成如下不完整的频数分布表和频数分布直方图.
安全知识竞赛成绩频数分布表
成绩 分 频数 所占百分比
4
8
16
12
根据以上信息解答下列问题:
(1)本次调查的学生人数为
____,表中的____,
______;
50
10
(2)补全频数分布直方图;
【解】补全频数分布直方图如图.
(第9题)
(3)若将调查结果绘制成扇形统计图,
求成绩在“ ”的部分所对应
的扇形圆心角的度数.
安全知识竞赛成绩在“ ”
的人数占, .
答:成绩在“ ”的部分所对应的扇形圆心角的度
数为 .
返回
思想2 方程思想
10.某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、
丙三组进行,如图所示的两幅统计图反映了学生参加夏令营
的报名情况,请你根据图中的信息回答下列问题:
(1)该年级报名参加丙组的有____人.
25
(2)该年级报名参加本次活
动的总人数为多少?并补全
条形统计图.
【解】该年级报名参加本次活动的总人数为 .
参加乙组的人数为 .
补全条形统计图如图所示.
(第10题)
(3)根据实际情况,需从甲组抽
调部分学生到丙组,使丙组人数
是甲组人数的3倍,应从甲组抽调
多少人到丙组?
设应从甲组抽调人到丙组,列方程得 ,解
得 .
应从甲组抽调5人到丙组.
返回
[时间:60分钟 分值:100分]
一、选择题(每小题5分,共35分)
1. 在英文“”一句中,字母“ ”出现
的频率为( )
B
A. 0.1 B. 0.2 C. 0.3 D. 0.4
返回
2. [2025邢台月考]为了解我区初中生每天完成家庭作业所
花时间及质量情况,根据以下四个步骤完成调查:①制作并
发放调查问卷;②…;③分析数据;④得出结论,提出建议
和整改意见.其中“…”表示( )
A
A. 收集数据 B. 选择调查方式
C. 实施调查 D. 合理决策
返回
3. 以“平安中国”为主题的 中国(南京)
国际应急产业博览会于2025年5月 日在中国南京举办.
为了调查全校学生对此次博览会的了解情况,下列抽样调查
的样本代表性较好的是( )
D
A. 选择七年级全体学生进行调查
B. 选择八年级2个班的学生进行调查
C. 对九年级每个班按 的比例用抽签的方法确定被调查者
D. 选择全校七至九年级学号是6的整数倍的学生进行调查
返回
4. 学生的心理健康问题越来越受关注.为了解学生的心理健
康状况,某学校从4 000名学生中随机抽取400名学生进行问
卷调查,下列说法错误的是( )
A
A. 400名学生是样本的容量
B. 400名学生的心理健康状况是一个样本
C. 每名学生的心理健康状况是个体
D. 4 000名学生的心理健康状况是总体
返回
5. 某单位有职工100名,按年龄将所有职工分成8组,在
(岁)组的频数是32.若绘制扇形统计图,则这个组对
应的扇形圆心角度数为( )
C
A. B. C. D.
返回
6. 恩格尔系数是家庭食品支出占家庭消费总支出的百分比,它反映了一
个家庭生活水平的高低.小慧家平均每月水电气支出600元,文化消费支出
1 200元,结合以下信息,小慧家属于 ( )
家庭类型 恩格尔系数
富裕家庭 小于
小康家庭
温饱家庭
贫困家庭 大于
A. 富裕家庭 B. 小康家庭
C. 温饱家庭 D. 贫困家庭
A
返回
7. 为提高学生的课外阅读水平,某市各中学开展了“我的梦,中国梦”课
外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从
中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频
数分布直方图(每组含后一个边界值,不含前一个边界值),有下列说法:
①这次调查属于普查;
②这次调查共抽取了200名学生;
③这次调查每日课外阅读所用时间在 的人数最少;
④这次调查每日课外阅读所用时间在的人数占所调查总人数的 .
A. ②③④ B. ①③④ C. ①②④ D. ①②③
A
其中正确的有( )
返回
二、填空题(每小题6分,共24分)
8. 2024年10月30日4时27分,搭载神舟十
九号载人飞船的长征二号 遥十九运载火箭在酒泉卫星发射
中心点火发射,约10分钟后,神舟十九号载人飞船与火箭成
功分离,进入预定轨道,发射取得圆满成功.调查长征二号
遥十九运载火箭零件的质量,适合采用______(填“普查”或
“抽样调查”).
普查
返回
9.某校为了解本校学生每周阅读课外书籍
的时间,对本校全体学生进行了调查,并
绘制成如图所示的直方图,那么图中这五
个小长方形的面积之和为___.
1
返回
10.某校为了解学生在校用午餐所需的时间,抽查了20名学生
在校用午餐所花的时间,获得如下数据(单位:分):
9,12,15,10,16,18,19,18,20,38,22,25,20,
18,18,20,15,16,21,16.
若将这些数据分为6组,制作频数分布表,则频数最大的组是 .
14分 分(包括14分,不包括19分)
返回
11.我市开展“美丽商城,创卫同行”活动,某校倡议学生利用
双休日在某公园参加义务劳动,为了解学生的劳动情况,学
校随机调查了部分学生的劳动时间,并用得到的数据绘制了
如图不完整的统计图,根据图中信息可知扇形统计图中的“
”部分对应的圆心角的度数是______.
【点拨】,劳动时间为 的人数为
, ,即扇形统计
图中的“”部分对应的圆心角的度数是 .
返回
三、解答题(共41分)
12.(15分)某市开展“讲文明、
树新风”知识竞赛活动,某校组织
了一次知识竞赛,赛后发现所有
参与者的成绩(总分100分)均不
低于50分,为了解本次竞赛的成
绩分布情况,随机抽取若干名参
与者的成绩进行整理,并绘制了如下两幅不完整的统计图表.
分数段(成绩为 分) 频数 频率
16 0.08
0.31
72 0.36
12
请你根据统计图表解答下列问题:
(1)此次抽样调查的样本容量是_____,____,
_____,____, _____.
200
62
0.06
38
0.19
(2)请补全参与者成绩分布直方图.
【解】补全参与者成绩分布直
方图如图所示.
(第12题)
(3)竞赛按照分数由高到低共设置一、
二、三等奖,如果有 的参与者能
获得一等奖,那么一等奖的最低分数
线是多少?
分数段在 和
的频率分别为, ,
,
一等奖的最低分数线是80分.
返回
13.(12分) 目前,全球淡水资源分布不均、
总量不足是人类面临的共同问题.某市在实施居民用水定额管
理前,通过简单随机抽样对居民生活用水情况进行了调查,获
得了若干户家庭去年的月均用水量数据(单位: ),绘制出
了如下不完整的频数分布表、频数分布直方图和扇形统计图.
月均用水 量/
频数 7 6
对应的扇 形区域
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并
求出扇形统计图中 的圆心角
的度数.
【解】抽取的总数为
,
B的频数为 ,
C的频数为 ,
E的频数为
.
补全频数分布直方图如图.
(第13题)
扇形统计图中的圆心角的度数为 .
(2)为了鼓励节约用水,要确定一个月均用水量的标准,
超出这个标准的部分按1.5倍价格收费,若要使该市 的家
庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?
并说明理由.
要使该市 的家庭水费支出不受影响,家庭月均用水量应
该定为 .理由如下:
月均用水量不超过的家庭有 (户),
.
返回
14.(14分)小婷利用统计知识分析《春
秋经传引得》《三国志》《汉书》《后
汉书》《史记》五本古文经典和某期现
代汉语文本《人民日报》的词汇长度、
词汇数量(单位:个)分布情况,研究
古人与现代人在撰写文章时的用词习惯,
由于十字词以上的词汇数量过少,所以
不做研究.下面给出了部分信息:
根据以上信息,回答下列问题:
(1)五本古文经典中词汇长度数量最
多的是____字词,其次是三字词;
二
(2)《后汉书》共出现词汇19 036个,
计算五本古文经典的词汇数量总数为多少
个;
【解】 ,
(个).
答:五本古文经典的词汇数量总数为
76 144个.
(3)通过分析古今的词汇长度、词汇
数量分布情况,说明古人与现代人在撰
写文章时用词习惯的共同点(写出一条
即可).
古人与现代人在撰写文章时都更倾向于
用二字词、三字词.(答案合理即可)
返回
谢谢观看!
章末复习
第14章 数据的收集与表示
【2025新教材】华东师大版数学 八年级上册
授课教师:********
班 级:********
时 间:********
第 14 章 数据的收集与表示章末复习
一、知识框架梳理
(一)数据的收集
收集意义:数据收集是获取信息的基础,为数据分析、决策提供依据,如企业依据消费者数据调整产品策略 ,学校通过学生数据优化教学。
常用方法
问卷调查法:适用于大规模数据收集,需注意问题设计避免引导性和歧义性,包含标题、指导语、问题和答案等结构。
访谈法:利于深入了解对象想法,分个别访谈和集体访谈,需提前准备提纲,营造良好氛围。
观察法:可直接获取行为现象,分参与式和非参与式,要明确观察对象、内容、时间和地点。
实验法:用于研究因果关系,遵循控制变量等原则,设置对照组和实验组。
(二)数据的表示
统计表:以表格形式呈现数据,结构包括标题、标目、数据和表注,能准确有条理地展示数据,便于对比分析。
统计图
条形统计图:用直条长短表示数量,直观反映数量多少,适合比较不同类别数据差异。
折线统计图:通过折线展示数据增减变化,可体现数量多少与变化趋势,常用于展示随时间等连续变量变化的数据。
扇形统计图:用扇形表示各部分占比,清晰呈现部分与总体比例关系,适用于展示份额分布。
象形统计图:利用形象图案表示数据,更直观有趣,常用于低龄受众或简单数据展示 。
二、典型例题解析
(一)数据收集方法的选择与应用
例 1:要了解全校学生对课后服务社团的喜好情况,应采用哪种数据收集方法?
分析:全校学生数量较多,适合采用问卷调查法,可设计包含各类社团选项的问卷,快速收集大量数据。
解答:选择问卷调查法,设计问卷时注意涵盖所有社团类型,问题表述清晰,便于学生作答。
(二)数据表示方法的选择与绘制
例 2:某商场统计了近半年每月的销售额,分别为:1 月 80 万元,2 月 95 万元,3 月 100 万元,4 月 120 万元,5 月 110 万元,6 月 130 万元。请选择合适的统计图表示这些数据,并绘制出来。
分析:数据是随时间变化的销售额,体现的是数据的增减趋势,所以适合用折线统计图。
解答:
绘制横纵轴,横轴表示月份,纵轴表示销售额(单位:万元),标注刻度。
根据数据在对应位置描点,依次连接各点。
标注图表标题 “某商场近半年每月销售额统计图”。
例 3:某班级学生参加兴趣小组的情况如下:绘画组 15 人,书法组 10 人,音乐组 20 人,体育组 25 人。若要清晰展示各小组人数占总人数的比例关系,应选择哪种统计图?并计算各小组人数占比。
分析:需展示各部分在总体中的占比,应选择扇形统计图。先计算总人数,再分别计算各小组人数占比。
解答:
总人数:\(15 + 10 + 20 + 25 = 70\)(人)
绘画组占比:\(15 ·70 100\% 21.4\%\),对应圆心角:\(360 ° 21.4\% 77 °\)
书法组占比:\(10 ·70 100\% 14.3\%\),对应圆心角:\(360 ° 14.3\% 51 °\)
音乐组占比:\(20 ·70 100\% 28.6\%\),对应圆心角:\(360 ° 28.6\% 103 °\)
体育组占比:\(25 ·70 100\% 35.7\%\),对应圆心角:\(360 ° 35.7\% 128 °\)
绘制扇形统计图,标注各小组名称、占比及圆心角。
三、易错点提醒
数据收集
问卷调查设计问题时,避免出现模糊不清、引导性语句,确保数据真实有效。
根据调查对象和目的合理选择收集方法,如小范围深入调查适合访谈法,大规模普适合问卷调查法。
数据表示
制作统计图时,注意刻度均匀,比例恰当,避免因刻度设置不当导致数据展示偏差。
选择统计图类型要准确,如展示数量变化用折线统计图,比较数量多少用条形统计图,体现占比用扇形统计图。
四、综合练习
(一)基础巩固
学校想了解学生对食堂饭菜的满意度,最适合采用( )收集数据。
A. 观察法 B. 访谈法 C. 问卷调查法 D. 实验法
要统计某地区一周的气温变化情况,应绘制( )统计图。
A. 条形 B. 折线 C. 扇形 D. 象形
制作扇形统计图时,某部分占总体的\(30\%\),则该部分对应的圆心角是( )度。
(二)能力提升
某超市统计了四种饮料一个月的销售数量:可乐 120 瓶,雪碧 80 瓶,橙汁 100 瓶,绿茶 150 瓶。
请制作统计表表示这些数据。
选择合适的统计图绘制出来,并分析哪种饮料最受欢迎。
以下是某班级学生某次数学考试的成绩分布:优秀(85 分及以上)12 人,良好(70 - 84 分)20 人,中等(60 - 69 分)15 人,不及格(60 分以下)3 人。制作扇形统计图展示成绩分布情况,并计算各部分圆心角度数。
五、复习建议
对照知识框架,查漏补缺,确保对数据收集与表示的概念、方法清晰掌握。
整理做过的例题和练习题,分析错题原因,针对薄弱环节加强训练,尤其是数据表示方法的选择和统计图绘制。
关注生活中的数据收集与表示案例,尝试用所学知识进行分析和解读,提高知识应用能力。
这份复习资料涵盖知识、例题与练习。你可以说说对内容深度、练习量等方面的看法,若有其他需求,我会进一步优化。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
考点1 普查与抽样调查
1. “谁知盘中餐,粒粒皆辛苦”,学校为杜绝
舌尖上的浪费开展“光盘行动”活动,为了解七年级200名学生
参与此次活动的现状,采用抽样调查的方式来收集数据,则
抽取样本的方式比较合理的是( )
D
A. 选取50名男生 B. 选取一个班的50名学生
C. 选取50名女生 D. 随机选取50名学生
返回
2.下列调查中,适合用普查的是______,适合用抽样调查的
是__________.
①了解全国青少年儿童的睡眠时间;
②了解乘客是否携带危险物品乘坐高铁;
③了解某班学生对“雷锋精神”的知晓率;
④了解某市居民对废电池的处理情况;
⑤了解黄河中某些鱼的数量;
⑥了解市民对某部电影的喜欢程度.
②③
①④⑤⑥
返回
考点2 总体、个体、样本和样本容量
3. 为弘扬中华优秀传统文化,倡导健康生活方式,某中学本
学期开设了校本课程“八段锦”,为了解学生对该课程的满意
度,在全校的1 000名学生中随机抽取了100名学生对该课程
的满意程度打分,下列说法正确的是( )
C
A. 样本容量为1 000
B. 总体是100名学生
C. 样本是抽取的100名学生所打的分数
D. 个体是被抽取的每一名学生
返回
考点3 频数与频率
4. “教育强国”四字的汉语拼音中,字母“ ”出现
的频率是( )
C
A. B. C. D.
5.一次数学测试后,某班80名学生的成绩被分为5组,第一至
第四组的频数分别为8,10,16,14,则第五组的频率是____.
0.4
返回
考点4 频数分布直方图(表)
6.某同学统计了他上周通话次数及每次的通话时间,并列出
如下频数分布表:
通话时间 分钟
通话次数 (频数) 26 14 7 2 1
则通话时间超过6分钟的频率是____.
0.2
返回
7.某路段的雷达测速器对一段时间内通过
的汽车进行测速,将监测到的数据加以整
理,得到如下不完整的图表:
时速段/ 总
计
频数 10 36 ___ ___ 20 200
百分比 ___ 1
注:“”表示时速大于或等于 且
小于 ,其他类同.
(1)请你把表中的数据填写完整.
【解】填表如下.
时速段 总计
频数 10 36 78. . 56. . 20 200
百分比 1
. .
(2)补全频数分布直方图.
补全频数分布直方图如图.
(3)如果此路段汽车时速达
到或超过 即为违章,那
么违章车辆共有多少辆?
(辆).
答:违章车辆共有76辆.
返回
考点5 统计图的应用
8.去年3至8月份期间,,, 三种品牌空调的销售情况如
下列统计图所示,根据统计图,回答下列问题:
(1)3至8月份期间,___品牌空调销售量最多(填“”“ ”或
“”).8月份品牌空调销售量有_____台.扇形统计图中, 品
牌所对应的扇形的圆心角是_____度.
275
97.2
(2)8月份其他品牌的空调销
售总量是多少台?
【解】8月份空调销售总量为
(台),
月份其他品牌的空调销售
总量是221台.
(台),
返回
思想1 数形结合思想
9.某校进行了“交通法规要牢记,路过
街市别大意”交通安全知识竞赛,为了
解本校学生对交通安全知识的掌握情
况,随机抽取了部分学生的成绩
(单位:分),并将他们的成绩整理
成如下不完整的频数分布表和频数分布直方图.
安全知识竞赛成绩频数分布表
成绩 分 频数 所占百分比
4
8
16
12
根据以上信息解答下列问题:
(1)本次调查的学生人数为
____,表中的____,
______;
50
10
(2)补全频数分布直方图;
【解】补全频数分布直方图如图.
(第9题)
(3)若将调查结果绘制成扇形统计图,
求成绩在“ ”的部分所对应
的扇形圆心角的度数.
安全知识竞赛成绩在“ ”
的人数占, .
答:成绩在“ ”的部分所对应的扇形圆心角的度
数为 .
返回
思想2 方程思想
10.某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、
丙三组进行,如图所示的两幅统计图反映了学生参加夏令营
的报名情况,请你根据图中的信息回答下列问题:
(1)该年级报名参加丙组的有____人.
25
(2)该年级报名参加本次活
动的总人数为多少?并补全
条形统计图.
【解】该年级报名参加本次活动的总人数为 .
参加乙组的人数为 .
补全条形统计图如图所示.
(第10题)
(3)根据实际情况,需从甲组抽
调部分学生到丙组,使丙组人数
是甲组人数的3倍,应从甲组抽调
多少人到丙组?
设应从甲组抽调人到丙组,列方程得 ,解
得 .
应从甲组抽调5人到丙组.
返回
[时间:60分钟 分值:100分]
一、选择题(每小题5分,共35分)
1. 在英文“”一句中,字母“ ”出现
的频率为( )
B
A. 0.1 B. 0.2 C. 0.3 D. 0.4
返回
2. [2025邢台月考]为了解我区初中生每天完成家庭作业所
花时间及质量情况,根据以下四个步骤完成调查:①制作并
发放调查问卷;②…;③分析数据;④得出结论,提出建议
和整改意见.其中“…”表示( )
A
A. 收集数据 B. 选择调查方式
C. 实施调查 D. 合理决策
返回
3. 以“平安中国”为主题的 中国(南京)
国际应急产业博览会于2025年5月 日在中国南京举办.
为了调查全校学生对此次博览会的了解情况,下列抽样调查
的样本代表性较好的是( )
D
A. 选择七年级全体学生进行调查
B. 选择八年级2个班的学生进行调查
C. 对九年级每个班按 的比例用抽签的方法确定被调查者
D. 选择全校七至九年级学号是6的整数倍的学生进行调查
返回
4. 学生的心理健康问题越来越受关注.为了解学生的心理健
康状况,某学校从4 000名学生中随机抽取400名学生进行问
卷调查,下列说法错误的是( )
A
A. 400名学生是样本的容量
B. 400名学生的心理健康状况是一个样本
C. 每名学生的心理健康状况是个体
D. 4 000名学生的心理健康状况是总体
返回
5. 某单位有职工100名,按年龄将所有职工分成8组,在
(岁)组的频数是32.若绘制扇形统计图,则这个组对
应的扇形圆心角度数为( )
C
A. B. C. D.
返回
6. 恩格尔系数是家庭食品支出占家庭消费总支出的百分比,它反映了一
个家庭生活水平的高低.小慧家平均每月水电气支出600元,文化消费支出
1 200元,结合以下信息,小慧家属于 ( )
家庭类型 恩格尔系数
富裕家庭 小于
小康家庭
温饱家庭
贫困家庭 大于
A. 富裕家庭 B. 小康家庭
C. 温饱家庭 D. 贫困家庭
A
返回
7. 为提高学生的课外阅读水平,某市各中学开展了“我的梦,中国梦”课
外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从
中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频
数分布直方图(每组含后一个边界值,不含前一个边界值),有下列说法:
①这次调查属于普查;
②这次调查共抽取了200名学生;
③这次调查每日课外阅读所用时间在 的人数最少;
④这次调查每日课外阅读所用时间在的人数占所调查总人数的 .
A. ②③④ B. ①③④ C. ①②④ D. ①②③
A
其中正确的有( )
返回
二、填空题(每小题6分,共24分)
8. 2024年10月30日4时27分,搭载神舟十
九号载人飞船的长征二号 遥十九运载火箭在酒泉卫星发射
中心点火发射,约10分钟后,神舟十九号载人飞船与火箭成
功分离,进入预定轨道,发射取得圆满成功.调查长征二号
遥十九运载火箭零件的质量,适合采用______(填“普查”或
“抽样调查”).
普查
返回
9.某校为了解本校学生每周阅读课外书籍
的时间,对本校全体学生进行了调查,并
绘制成如图所示的直方图,那么图中这五
个小长方形的面积之和为___.
1
返回
10.某校为了解学生在校用午餐所需的时间,抽查了20名学生
在校用午餐所花的时间,获得如下数据(单位:分):
9,12,15,10,16,18,19,18,20,38,22,25,20,
18,18,20,15,16,21,16.
若将这些数据分为6组,制作频数分布表,则频数最大的组是 .
14分 分(包括14分,不包括19分)
返回
11.我市开展“美丽商城,创卫同行”活动,某校倡议学生利用
双休日在某公园参加义务劳动,为了解学生的劳动情况,学
校随机调查了部分学生的劳动时间,并用得到的数据绘制了
如图不完整的统计图,根据图中信息可知扇形统计图中的“
”部分对应的圆心角的度数是______.
【点拨】,劳动时间为 的人数为
, ,即扇形统计
图中的“”部分对应的圆心角的度数是 .
返回
三、解答题(共41分)
12.(15分)某市开展“讲文明、
树新风”知识竞赛活动,某校组织
了一次知识竞赛,赛后发现所有
参与者的成绩(总分100分)均不
低于50分,为了解本次竞赛的成
绩分布情况,随机抽取若干名参
与者的成绩进行整理,并绘制了如下两幅不完整的统计图表.
分数段(成绩为 分) 频数 频率
16 0.08
0.31
72 0.36
12
请你根据统计图表解答下列问题:
(1)此次抽样调查的样本容量是_____,____,
_____,____, _____.
200
62
0.06
38
0.19
(2)请补全参与者成绩分布直方图.
【解】补全参与者成绩分布直
方图如图所示.
(第12题)
(3)竞赛按照分数由高到低共设置一、
二、三等奖,如果有 的参与者能
获得一等奖,那么一等奖的最低分数
线是多少?
分数段在 和
的频率分别为, ,
,
一等奖的最低分数线是80分.
返回
13.(12分) 目前,全球淡水资源分布不均、
总量不足是人类面临的共同问题.某市在实施居民用水定额管
理前,通过简单随机抽样对居民生活用水情况进行了调查,获
得了若干户家庭去年的月均用水量数据(单位: ),绘制出
了如下不完整的频数分布表、频数分布直方图和扇形统计图.
月均用水 量/
频数 7 6
对应的扇 形区域
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并
求出扇形统计图中 的圆心角
的度数.
【解】抽取的总数为
,
B的频数为 ,
C的频数为 ,
E的频数为
.
补全频数分布直方图如图.
(第13题)
扇形统计图中的圆心角的度数为 .
(2)为了鼓励节约用水,要确定一个月均用水量的标准,
超出这个标准的部分按1.5倍价格收费,若要使该市 的家
庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?
并说明理由.
要使该市 的家庭水费支出不受影响,家庭月均用水量应
该定为 .理由如下:
月均用水量不超过的家庭有 (户),
.
返回
14.(14分)小婷利用统计知识分析《春
秋经传引得》《三国志》《汉书》《后
汉书》《史记》五本古文经典和某期现
代汉语文本《人民日报》的词汇长度、
词汇数量(单位:个)分布情况,研究
古人与现代人在撰写文章时的用词习惯,
由于十字词以上的词汇数量过少,所以
不做研究.下面给出了部分信息:
根据以上信息,回答下列问题:
(1)五本古文经典中词汇长度数量最
多的是____字词,其次是三字词;
二
(2)《后汉书》共出现词汇19 036个,
计算五本古文经典的词汇数量总数为多少
个;
【解】 ,
(个).
答:五本古文经典的词汇数量总数为
76 144个.
(3)通过分析古今的词汇长度、词汇
数量分布情况,说明古人与现代人在撰
写文章时用词习惯的共同点(写出一条
即可).
古人与现代人在撰写文章时都更倾向于
用二字词、三字词.(答案合理即可)
返回
谢谢观看!
