(进阶篇)五年级暑假分层作业测试卷:第五至七单元(含解析)-2024-2025学年下学期小学数学苏教版
文档属性
| 名称 | (进阶篇)五年级暑假分层作业测试卷:第五至七单元(含解析)-2024-2025学年下学期小学数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 19:54:40 | ||
图片预览



文档简介
(进阶篇)五年级暑假分层作业测试卷:第五至七单元(含解析)-2024-2025学年下学期小学数学苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,把一个长方形分成左中右三等份,再把中间部分平均分成2份,把右边平均分成3份,那么图中涂色部分的面积是原长方形面积的( )。
A. B. C. D.
2.圆规两脚之间的距离是4厘米,这时用圆规画出的圆的面积是( )平方厘米。
A.12.56 B.18.84 C.25.12 D.50.24
3.大圆的半径与小圆的直径相等,大圆的周长是小圆的( )倍。
A.4 B.2 C.1
4.如图,在正方形内画一个最大的圆,正方形的周长是圆直径的4倍。在圆内再画一个正六边形,正六边形的顶点都在圆上,则正六边形的周长是圆直径的( )倍。
A.3 B.4 C.6 D.9
5.一个直径是80m的圆形花坛中间有一个尺寸是60m×20m的长方形蓄水池,求花坛的面积,列式正确的是( )。
A. B. C. D.
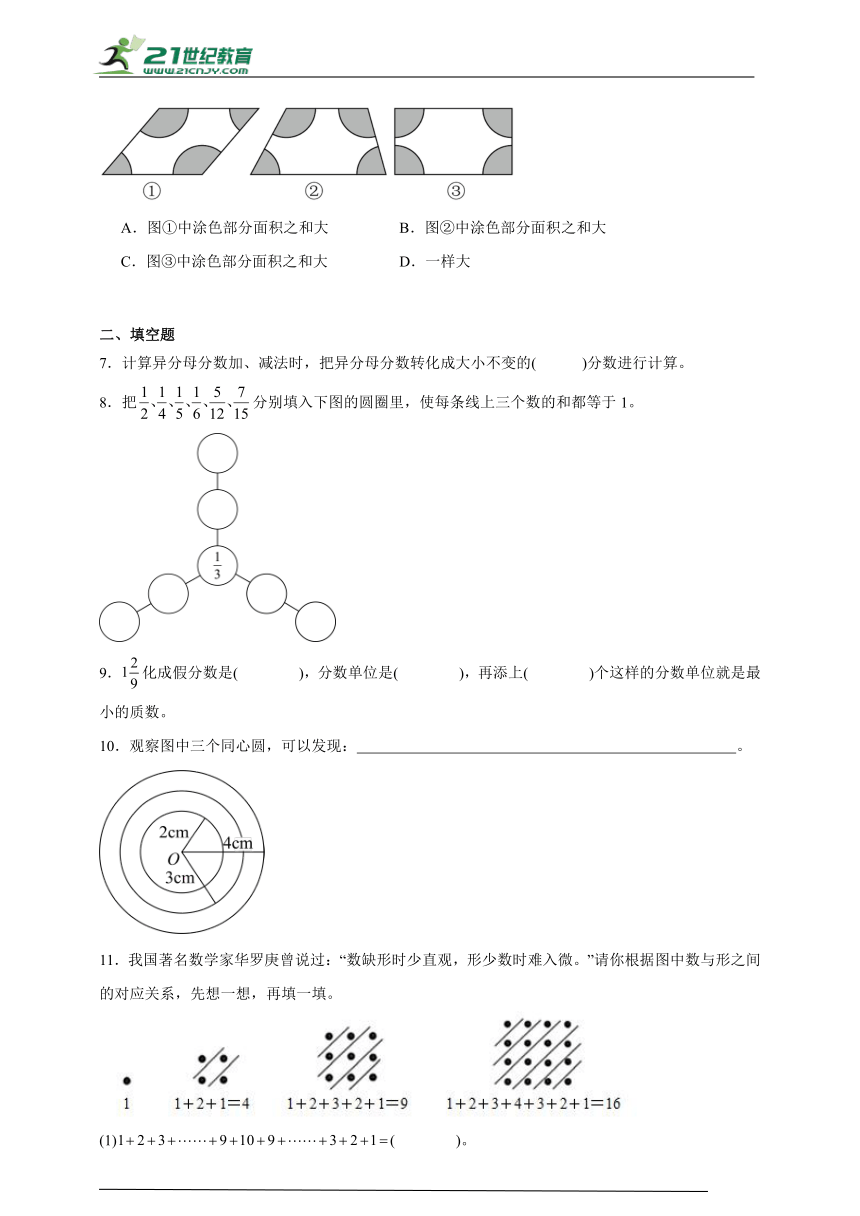
6.下面三幅图中每个扇形的半径都是1厘米,比较每幅图中涂色部分的面积之和,结果是( )。
A.图①中涂色部分面积之和大 B.图②中涂色部分面积之和大
C.图③中涂色部分面积之和大 D.一样大
二、填空题
7.计算异分母分数加、减法时,把异分母分数转化成大小不变的( )分数进行计算。
8.把分别填入下图的圆圈里,使每条线上三个数的和都等于1。
9.化成假分数是( ),分数单位是( ),再添上( )个这样的分数单位就是最小的质数。
10.观察图中三个同心圆,可以发现: 。
11.我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微。”请你根据图中数与形之间的对应关系,先想一想,再填一填。
(1)( )。
(2)( )。
12.学校、乐乐家和图书馆都在光明路同侧。学校离乐乐家,图书馆离乐乐家km,学校到图书馆的距离可能是( )km,也可能是( )km。
13.福建土楼是我国特有的建筑,土楼的底面是圆形。沿着土楼外围走一圈需要走219.8m,那么这座土楼的占地面积是( )m2。
14.如图,三角形ABC是直角三角形,AB是圆的直径,AB长10厘米,已知阴影乙部分比阴影甲部分的面积少6平方厘米。那么BC的长是( )厘米,三角形ABC的面积是( )平方厘米。
三、判断题
15.相等的圆中,扇形的大小与圆心角的大小有关。( )
16.长方形、圆形和等腰三角形都是轴对称图形。( )
17.在同一个圆中,扇形的大小与圆心角有关。( )
18.一条7千米长的公路,已经修了千米,还剩下全长的没有修。( )
19.=1。( )
四、计算题
20.直接写出得数。
5÷8=
0.72÷9=
21.解方程。
五、作图题
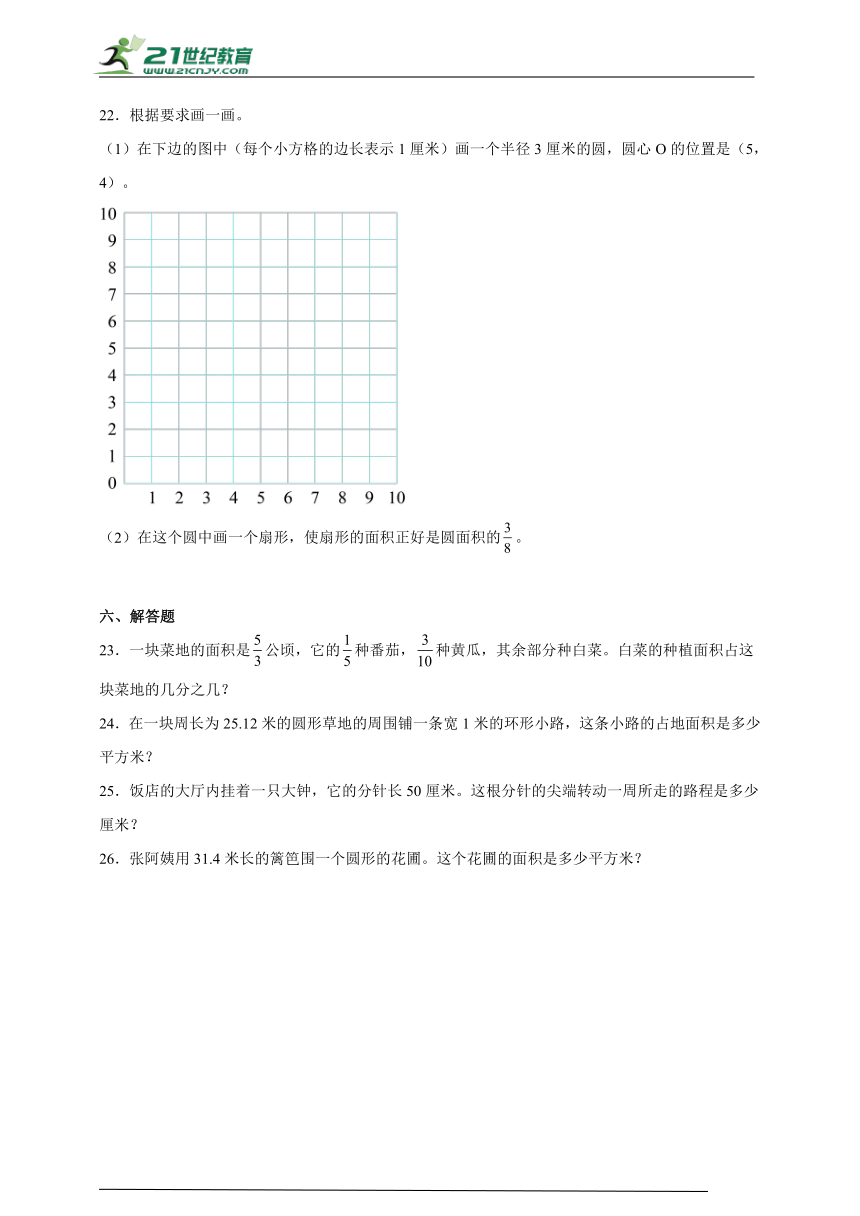
22.根据要求画一画。
(1)在下边的图中(每个小方格的边长表示1厘米)画一个半径3厘米的圆,圆心O的位置是(5,4)。
(2)在这个圆中画一个扇形,使扇形的面积正好是圆面积的。
六、解答题
23.一块菜地的面积是公顷,它的种番茄,种黄瓜,其余部分种白菜。白菜的种植面积占这块菜地的几分之几?
24.在一块周长为25.12米的圆形草地的周围铺一条宽1米的环形小路,这条小路的占地面积是多少平方米?
25.饭店的大厅内挂着一只大钟,它的分针长50厘米。这根分针的尖端转动一周所走的路程是多少厘米?
26.张阿姨用31.4米长的篱笆围一个圆形的花圃。这个花圃的面积是多少平方米?
《(进阶篇)五年级暑假分层作业测试卷:第五至七单元(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
题号 1 2 3 4 5 6
答案 B D B A D D
1.B
【分析】根据题意,三个大小相同的长方形拼在一起,组成一个大长方形,则第二个涂色部分占整个长方形的1÷6=;第三个涂色部分占长方形的2÷9=。用加法求涂色部分占整个长方形的几分之几即可解答。
【详解】+=+=
图中涂色部分的面积是原长方形面积的。
故答案为:B
2.D
【分析】用圆规画圆时,圆规两脚之间的距离就是圆的半径,根据圆的面积=πr2,代入数据计算即可。
【详解】
=
(平方厘米)
即该圆的面积是50.24平方厘米;
故答案为:D
3.B
【分析】圆的周长=πd=2πr,据此可以假设大圆的半径是2,则小圆的直径也是2,根据周长公式分别算出大圆和小圆的周长,最后用大圆的周长除以小圆的周长即可。
【详解】假设大圆的半径和小圆的直径都是2。
2×2×3.14
=4×3.14
=12.56
2×3.14=6.28
12.56÷6.28=2
大圆的半径与小圆的直径相等,大圆的周长是小圆的2倍。
故答案为:B
4.A
【分析】看图可知,正六边形被分割成6个等边三角形,所以正六边形的边长是圆的半径,正六边形的周长是半径的6倍。用r来表示圆的半径,那么正六边形的周长是6r,圆直径是2r。将正六边形的周长除以圆直径,求出正六边形的周长是圆直径的几倍。
【详解】6r÷2r=3
所以正六边形的周长是圆直径的3倍。
故答案为:A
5.D
【分析】观察图形可知,花坛的面积=圆的面积-长方形的面积,根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据列式即可。
【详解】(80÷2)2π-60×20
=402π-60×20
=(1600π-1200)(m2)
所以,求花坛的面积,列式正确的是(80÷2)2π-60×20。
故答案为:D
6.D
【分析】平行四边形、梯形和长方形都是四边形,内角和都是360°,则每幅图中的扇形都可以拼成半径是1厘米的圆,据此解答即可。
【详解】根据分析可得,三幅图的涂色面积之和都是半径为1厘米的圆的面积。
故答案为:D
【点睛】本题考查平行四边形、梯形、长方形的内角和,圆的面积,解答本题的关键是掌握这些图形的特征。
7.同分母
【详解】计算异分母分数加、减法时,把异分母分数转化成大小不变的同分母分数后再进行计算。
例:
8.见详解
【分析】由图可知,已经给出了中间数,1-=,只要使给出的两个数的和都是即可。利用异分母分数相加的计算法则,找出符合要求的数。
【详解】1-=
+=+==
+=+==
+=+==
所以,填数如下:
(答案不唯一)
9. 7
【分析】带分数化假分数,分母不变,分子为整数部分与分母的积再加上原分子的和;
把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位,分数的分母是几,分数单位就是几分之一;
最小的质数是2,用2减去得,里有7个;
据此解答即可。
【详解】1×9+2
=9+2
=11
2-=-=
所以,化成假分数是,分数单位是,再添上7个这样的分数单位就是最小的质数。
10.圆的位置没有变化,大小发生变化,即半径依次增加1cm
【分析】根据圆的位置,以及圆的大小,即圆的半径之间的变化,进行解答。
【详解】圆的位置没有变化,大小发生变化,即半径依次增加1cm。(说法合理即可)
11.(1)100
(2)256
【分析】观察所给的算式可知,1=12;1+2+1=4=22;1+2+3+2+1=9=32;1+2+3+4+3+2+1=16=42;由此可知,算式的和等于算式中间那个最大加数的平方,据此解答。
【详解】(1)1+2+3+……+9+10+9+……+3+2+1=102=100
(2)(1+2+3+……+15)×2+16
=1+2+3+……+15+16+15+……+3+2+1
=162
=256
【点睛】本题考查数与形结合的规律,根据观察所给的四组数据,找出算式结果与算式中加数的关系,是解答本题的关键。
12.
【分析】因为学校、乐乐家和图书馆在光明路同侧:所以存在两种位置关系,一种是图书馆在乐乐家和学校之间,另一种是乐乐家在图书馆和学校之间。我们通过分析这两种位置关系下学校与图书馆的距离来求解。
【详解】当图书馆在乐乐家和学校之间时:已知学校离乐乐家km,图书馆离乐乐家km 。
此时学校到图书馆的距离就是学校到乐乐家的距离减去图书馆到乐乐家的距离:
-=-=(km)
当乐乐家在图书馆和学校之间时:同样已知学校离乐乐家km,图书馆离乐乐家km。
这时学校到图书馆的距离就是学校到乐乐家的距离加上图书馆到乐乐家的距:
+=+=(km)
所以学校到图书馆的距离可能是km,也可能是km。
13.3846.5
【分析】根据圆的周长=圆周率×直径,用土楼的底面周长219.8m除以3.14,求出底面圆的直径,再除以2求出半径,再根据圆的面积=圆周率×半径的平方解答即可。
【详解】219.8÷3.14÷2
=70÷2
=35(m)
3.14×
=3.14×1225
=3846.5()
所以这座土楼的占地面积是3846.5。
14. 6.65 33.25
【分析】看图可知,半圆的面积-三角形ABC的面积是=阴影甲部分的面积-阴影乙部分的面积=6平方厘米,设BC的长是x厘米,根据半圆的面积-三角形ABC的面积是=6平方厘米,列出方程求出x的值是BC的长,再根据三角形面积=底×高÷2,求出三角形ABC的面积。
【详解】解:设BC的长是x厘米。
3.14×(10÷2)2÷2-10x÷2=6
3.14×52÷2-5x=6
3.14×25÷2-5x=6
39.25-5x+5x=6+5x
6+5x=39.25
6+5x-6=39.25-6
5x=33.25
5x÷5=33.25÷5
x=6.65
10×6.65÷2=33.25(平方厘米)
BC的长是6.65厘米,三角形ABC的面积是33.25平方厘米。
【点睛】关键是掌握并灵活运用圆和三角形面积公式,用方程解决问题的关键是找到等量关系。
15.√
【分析】同圆或等圆的大小相等,由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形,扇形是圆的一部分,扇形的面积=πr2。
【详解】根据扇形的面积公式可知,扇形的大小和半径及圆心角有关,同圆或等圆的半径相等,所以在同圆或等圆中,扇形的大小与圆心角的大小有关,圆心角越大,扇形越大;原题说法正确。
故答案为:√
16.√
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】
长方形有2条对称轴,是轴对称图形;
圆有无数条对称轴,是轴对称图形;
等腰三角形有1条对称轴,是轴对称图形;
所以,长方形、圆形和等腰三角形都是轴对称图形。
原题说法正确。
故答案为:√
【点睛】掌握轴对称图形的意义及特点,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合。
17.√
【分析】在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。圆心角越大,扇形越大;圆心角越小,扇形越小。
【详解】根据分析可知,在同一个圆中,扇形的大小与圆心角有关。
原题干说法正确。
故答案为:√
18.×
【分析】一条7千米长的公路,已经修了千米,分数后有单位,所以不是分率,直接用7-,即可得出还剩多少千米没修。据此解答。
【详解】7-=(千米)
所以一条7千米长的公路,已经修了千米,还剩下全长的千米没有修。
故答案为:×
19.√
【分析】先去括号,再运用加法的交换律、结合律,减法的性质进行简算。
【详解】
=0+1
=1
所以原题计算正确。
故答案为:√
【点睛】本题考查了分数的加、减混合运算,熟练掌握加法运算定律是解题的关键。
20.;;;
;0.36;0.08;
【详解】略。
21.;;
【分析】根据等式的性质解方程。
(1)先把方程化简成,然后方程两边同时除以,求出方程的解;
(2)方程两边同时减去,求出方程的解;
(3)先把方程化简成,然后方程两边同时除以,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
22.(1)见详解
(2)见详解
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,找出圆心所在位置,以半径3厘米画圆。
(2)根据分数的意义,把360度平均分成8份,取这样的3份计算出扇形的圆心角的度数,再在圆上画的扇形即可。
【详解】(1)据分析作图如下:
(2)
作图如下:
(答案不唯一)
23.
【分析】求白菜的种植面积占这块菜地的几分之几?那么我们首先应该把这块菜地整体看作单位“1”,其中,番茄占,黄瓜占,那么剩余的就是白菜所占的分率,因此只需用1减去,再减去即可。
【详解】1--
=-
=
答:白菜的种植面积占这块菜地的。
24.28.26平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆形草地的半径;求小路的占地面积就是求圆环的面积,根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,即可解答。
【详解】25.12÷3.14÷2
=8÷2
=4(米)
3.14×[(4+1)2-42]
=3.14×[52-42]
=3.14×[25-16]
=3.14×9
=28.26(平方米)
答:这条小路的占地面积是28.26平方米。
25.314厘米
【分析】求这根分针的尖端转动一周所走的路程,就是求半径是50厘米圆的周长;根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】3.14×50×2
=157×2
=314(厘米)
答:这根分针的尖端转动一周所走的路程是314厘米。
【点睛】本题主要考查圆的周长公式的灵活运用,关键是熟记公式。
26.78.5平方米
【分析】根据题意可知,篱笆的长就是这个圆形的花圃的周长,根据圆的周长公式:周长=π×2×半径,半径=圆的周长÷2÷π,代入数据,求出圆形的花圃的半径,再根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】31.4÷2÷3.14
=15.7÷3.14
=5(米)
3.14×52
=3.14×25
=78.5(平方米)
答:这个花圃的面积是78.5平方米。
【点睛】熟练掌握和灵活运用圆的周长公式和面积公式是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,把一个长方形分成左中右三等份,再把中间部分平均分成2份,把右边平均分成3份,那么图中涂色部分的面积是原长方形面积的( )。
A. B. C. D.
2.圆规两脚之间的距离是4厘米,这时用圆规画出的圆的面积是( )平方厘米。
A.12.56 B.18.84 C.25.12 D.50.24
3.大圆的半径与小圆的直径相等,大圆的周长是小圆的( )倍。
A.4 B.2 C.1
4.如图,在正方形内画一个最大的圆,正方形的周长是圆直径的4倍。在圆内再画一个正六边形,正六边形的顶点都在圆上,则正六边形的周长是圆直径的( )倍。
A.3 B.4 C.6 D.9
5.一个直径是80m的圆形花坛中间有一个尺寸是60m×20m的长方形蓄水池,求花坛的面积,列式正确的是( )。
A. B. C. D.
6.下面三幅图中每个扇形的半径都是1厘米,比较每幅图中涂色部分的面积之和,结果是( )。
A.图①中涂色部分面积之和大 B.图②中涂色部分面积之和大
C.图③中涂色部分面积之和大 D.一样大
二、填空题
7.计算异分母分数加、减法时,把异分母分数转化成大小不变的( )分数进行计算。
8.把分别填入下图的圆圈里,使每条线上三个数的和都等于1。
9.化成假分数是( ),分数单位是( ),再添上( )个这样的分数单位就是最小的质数。
10.观察图中三个同心圆,可以发现: 。
11.我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微。”请你根据图中数与形之间的对应关系,先想一想,再填一填。
(1)( )。
(2)( )。
12.学校、乐乐家和图书馆都在光明路同侧。学校离乐乐家,图书馆离乐乐家km,学校到图书馆的距离可能是( )km,也可能是( )km。
13.福建土楼是我国特有的建筑,土楼的底面是圆形。沿着土楼外围走一圈需要走219.8m,那么这座土楼的占地面积是( )m2。
14.如图,三角形ABC是直角三角形,AB是圆的直径,AB长10厘米,已知阴影乙部分比阴影甲部分的面积少6平方厘米。那么BC的长是( )厘米,三角形ABC的面积是( )平方厘米。
三、判断题
15.相等的圆中,扇形的大小与圆心角的大小有关。( )
16.长方形、圆形和等腰三角形都是轴对称图形。( )
17.在同一个圆中,扇形的大小与圆心角有关。( )
18.一条7千米长的公路,已经修了千米,还剩下全长的没有修。( )
19.=1。( )
四、计算题
20.直接写出得数。
5÷8=
0.72÷9=
21.解方程。
五、作图题
22.根据要求画一画。
(1)在下边的图中(每个小方格的边长表示1厘米)画一个半径3厘米的圆,圆心O的位置是(5,4)。
(2)在这个圆中画一个扇形,使扇形的面积正好是圆面积的。
六、解答题
23.一块菜地的面积是公顷,它的种番茄,种黄瓜,其余部分种白菜。白菜的种植面积占这块菜地的几分之几?
24.在一块周长为25.12米的圆形草地的周围铺一条宽1米的环形小路,这条小路的占地面积是多少平方米?
25.饭店的大厅内挂着一只大钟,它的分针长50厘米。这根分针的尖端转动一周所走的路程是多少厘米?
26.张阿姨用31.4米长的篱笆围一个圆形的花圃。这个花圃的面积是多少平方米?
《(进阶篇)五年级暑假分层作业测试卷:第五至七单元(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
题号 1 2 3 4 5 6
答案 B D B A D D
1.B
【分析】根据题意,三个大小相同的长方形拼在一起,组成一个大长方形,则第二个涂色部分占整个长方形的1÷6=;第三个涂色部分占长方形的2÷9=。用加法求涂色部分占整个长方形的几分之几即可解答。
【详解】+=+=
图中涂色部分的面积是原长方形面积的。
故答案为:B
2.D
【分析】用圆规画圆时,圆规两脚之间的距离就是圆的半径,根据圆的面积=πr2,代入数据计算即可。
【详解】
=
(平方厘米)
即该圆的面积是50.24平方厘米;
故答案为:D
3.B
【分析】圆的周长=πd=2πr,据此可以假设大圆的半径是2,则小圆的直径也是2,根据周长公式分别算出大圆和小圆的周长,最后用大圆的周长除以小圆的周长即可。
【详解】假设大圆的半径和小圆的直径都是2。
2×2×3.14
=4×3.14
=12.56
2×3.14=6.28
12.56÷6.28=2
大圆的半径与小圆的直径相等,大圆的周长是小圆的2倍。
故答案为:B
4.A
【分析】看图可知,正六边形被分割成6个等边三角形,所以正六边形的边长是圆的半径,正六边形的周长是半径的6倍。用r来表示圆的半径,那么正六边形的周长是6r,圆直径是2r。将正六边形的周长除以圆直径,求出正六边形的周长是圆直径的几倍。
【详解】6r÷2r=3
所以正六边形的周长是圆直径的3倍。
故答案为:A
5.D
【分析】观察图形可知,花坛的面积=圆的面积-长方形的面积,根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据列式即可。
【详解】(80÷2)2π-60×20
=402π-60×20
=(1600π-1200)(m2)
所以,求花坛的面积,列式正确的是(80÷2)2π-60×20。
故答案为:D
6.D
【分析】平行四边形、梯形和长方形都是四边形,内角和都是360°,则每幅图中的扇形都可以拼成半径是1厘米的圆,据此解答即可。
【详解】根据分析可得,三幅图的涂色面积之和都是半径为1厘米的圆的面积。
故答案为:D
【点睛】本题考查平行四边形、梯形、长方形的内角和,圆的面积,解答本题的关键是掌握这些图形的特征。
7.同分母
【详解】计算异分母分数加、减法时,把异分母分数转化成大小不变的同分母分数后再进行计算。
例:
8.见详解
【分析】由图可知,已经给出了中间数,1-=,只要使给出的两个数的和都是即可。利用异分母分数相加的计算法则,找出符合要求的数。
【详解】1-=
+=+==
+=+==
+=+==
所以,填数如下:
(答案不唯一)
9. 7
【分析】带分数化假分数,分母不变,分子为整数部分与分母的积再加上原分子的和;
把单位“1”平均分成若干份,这样的一份或几份都可以用分数来表示,表示其中一份的数叫作分数单位,分数的分母是几,分数单位就是几分之一;
最小的质数是2,用2减去得,里有7个;
据此解答即可。
【详解】1×9+2
=9+2
=11
2-=-=
所以,化成假分数是,分数单位是,再添上7个这样的分数单位就是最小的质数。
10.圆的位置没有变化,大小发生变化,即半径依次增加1cm
【分析】根据圆的位置,以及圆的大小,即圆的半径之间的变化,进行解答。
【详解】圆的位置没有变化,大小发生变化,即半径依次增加1cm。(说法合理即可)
11.(1)100
(2)256
【分析】观察所给的算式可知,1=12;1+2+1=4=22;1+2+3+2+1=9=32;1+2+3+4+3+2+1=16=42;由此可知,算式的和等于算式中间那个最大加数的平方,据此解答。
【详解】(1)1+2+3+……+9+10+9+……+3+2+1=102=100
(2)(1+2+3+……+15)×2+16
=1+2+3+……+15+16+15+……+3+2+1
=162
=256
【点睛】本题考查数与形结合的规律,根据观察所给的四组数据,找出算式结果与算式中加数的关系,是解答本题的关键。
12.
【分析】因为学校、乐乐家和图书馆在光明路同侧:所以存在两种位置关系,一种是图书馆在乐乐家和学校之间,另一种是乐乐家在图书馆和学校之间。我们通过分析这两种位置关系下学校与图书馆的距离来求解。
【详解】当图书馆在乐乐家和学校之间时:已知学校离乐乐家km,图书馆离乐乐家km 。
此时学校到图书馆的距离就是学校到乐乐家的距离减去图书馆到乐乐家的距离:
-=-=(km)
当乐乐家在图书馆和学校之间时:同样已知学校离乐乐家km,图书馆离乐乐家km。
这时学校到图书馆的距离就是学校到乐乐家的距离加上图书馆到乐乐家的距:
+=+=(km)
所以学校到图书馆的距离可能是km,也可能是km。
13.3846.5
【分析】根据圆的周长=圆周率×直径,用土楼的底面周长219.8m除以3.14,求出底面圆的直径,再除以2求出半径,再根据圆的面积=圆周率×半径的平方解答即可。
【详解】219.8÷3.14÷2
=70÷2
=35(m)
3.14×
=3.14×1225
=3846.5()
所以这座土楼的占地面积是3846.5。
14. 6.65 33.25
【分析】看图可知,半圆的面积-三角形ABC的面积是=阴影甲部分的面积-阴影乙部分的面积=6平方厘米,设BC的长是x厘米,根据半圆的面积-三角形ABC的面积是=6平方厘米,列出方程求出x的值是BC的长,再根据三角形面积=底×高÷2,求出三角形ABC的面积。
【详解】解:设BC的长是x厘米。
3.14×(10÷2)2÷2-10x÷2=6
3.14×52÷2-5x=6
3.14×25÷2-5x=6
39.25-5x+5x=6+5x
6+5x=39.25
6+5x-6=39.25-6
5x=33.25
5x÷5=33.25÷5
x=6.65
10×6.65÷2=33.25(平方厘米)
BC的长是6.65厘米,三角形ABC的面积是33.25平方厘米。
【点睛】关键是掌握并灵活运用圆和三角形面积公式,用方程解决问题的关键是找到等量关系。
15.√
【分析】同圆或等圆的大小相等,由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形,扇形是圆的一部分,扇形的面积=πr2。
【详解】根据扇形的面积公式可知,扇形的大小和半径及圆心角有关,同圆或等圆的半径相等,所以在同圆或等圆中,扇形的大小与圆心角的大小有关,圆心角越大,扇形越大;原题说法正确。
故答案为:√
16.√
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
【详解】
长方形有2条对称轴,是轴对称图形;
圆有无数条对称轴,是轴对称图形;
等腰三角形有1条对称轴,是轴对称图形;
所以,长方形、圆形和等腰三角形都是轴对称图形。
原题说法正确。
故答案为:√
【点睛】掌握轴对称图形的意义及特点,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合。
17.√
【分析】在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。圆心角越大,扇形越大;圆心角越小,扇形越小。
【详解】根据分析可知,在同一个圆中,扇形的大小与圆心角有关。
原题干说法正确。
故答案为:√
18.×
【分析】一条7千米长的公路,已经修了千米,分数后有单位,所以不是分率,直接用7-,即可得出还剩多少千米没修。据此解答。
【详解】7-=(千米)
所以一条7千米长的公路,已经修了千米,还剩下全长的千米没有修。
故答案为:×
19.√
【分析】先去括号,再运用加法的交换律、结合律,减法的性质进行简算。
【详解】
=0+1
=1
所以原题计算正确。
故答案为:√
【点睛】本题考查了分数的加、减混合运算,熟练掌握加法运算定律是解题的关键。
20.;;;
;0.36;0.08;
【详解】略。
21.;;
【分析】根据等式的性质解方程。
(1)先把方程化简成,然后方程两边同时除以,求出方程的解;
(2)方程两边同时减去,求出方程的解;
(3)先把方程化简成,然后方程两边同时除以,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
22.(1)见详解
(2)见详解
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,找出圆心所在位置,以半径3厘米画圆。
(2)根据分数的意义,把360度平均分成8份,取这样的3份计算出扇形的圆心角的度数,再在圆上画的扇形即可。
【详解】(1)据分析作图如下:
(2)
作图如下:
(答案不唯一)
23.
【分析】求白菜的种植面积占这块菜地的几分之几?那么我们首先应该把这块菜地整体看作单位“1”,其中,番茄占,黄瓜占,那么剩余的就是白菜所占的分率,因此只需用1减去,再减去即可。
【详解】1--
=-
=
答:白菜的种植面积占这块菜地的。
24.28.26平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆形草地的半径;求小路的占地面积就是求圆环的面积,根据圆环的面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,即可解答。
【详解】25.12÷3.14÷2
=8÷2
=4(米)
3.14×[(4+1)2-42]
=3.14×[52-42]
=3.14×[25-16]
=3.14×9
=28.26(平方米)
答:这条小路的占地面积是28.26平方米。
25.314厘米
【分析】求这根分针的尖端转动一周所走的路程,就是求半径是50厘米圆的周长;根据圆的周长公式:周长=π×半径×2,代入数据,即可解答。
【详解】3.14×50×2
=157×2
=314(厘米)
答:这根分针的尖端转动一周所走的路程是314厘米。
【点睛】本题主要考查圆的周长公式的灵活运用,关键是熟记公式。
26.78.5平方米
【分析】根据题意可知,篱笆的长就是这个圆形的花圃的周长,根据圆的周长公式:周长=π×2×半径,半径=圆的周长÷2÷π,代入数据,求出圆形的花圃的半径,再根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】31.4÷2÷3.14
=15.7÷3.14
=5(米)
3.14×52
=3.14×25
=78.5(平方米)
答:这个花圃的面积是78.5平方米。
【点睛】熟练掌握和灵活运用圆的周长公式和面积公式是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
