五年级暑假月考测试卷:第二至三单元(含解析)-2024-2025学年下学期小学数学苏教版
文档属性
| 名称 | 五年级暑假月考测试卷:第二至三单元(含解析)-2024-2025学年下学期小学数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 360.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 19:59:20 | ||
图片预览


文档简介
五年级暑假月考测试卷:第二至三单元(含解析)-2024-2025学年下学期小学数学苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面的资料信息中,适合用折线统计图表示的是( )。
A.甜品店一天卖出各种奶茶的数量
B.某电视剧豆瓣评分变化情况
C.爸爸手机里各APP占用内存情况
2.下面算式的结果一定是奇数的是( )。
A.是非0自然数) B.
C.两个合数相加 D.所有质数的乘积
3.两个连续自然数,它们的积一定是( ),它们的和一定是( )。
A.偶数;奇数 B.奇数;合数 C.奇数;质数 D. 偶数;质数
4.下列等式不成立的是( )。
A.奇数+偶数=偶数 B.奇数+奇数=偶数
C.质数×合数=合数 D.偶数×奇数=偶数
5.在一条60米的长廊的一侧,每隔3米挂一个红灯笼,共挂了21个。现在要将每两个灯笼之间的间隔改为4米,共有( )个灯笼不要移动。
A.5 B.6 C.7 D.8
6.已知m÷n=7,m、n都是不为0的自然数,那么m和n的最大公因数是( )。
A.m B.n C.7 D.1
7.在新冠疫情流行期间,采用( )既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
A.条形统计图 B.折线统计图 C.扇形统计图 D.三种都可以
8.运动会开幕式上,五(1)班入场队列如下图。所有人入场后都参加了开幕式表演,表演时变换了队形。下面四个开幕式表演队形中,五(1)班的队形可能是( )。
A. B. C. D.
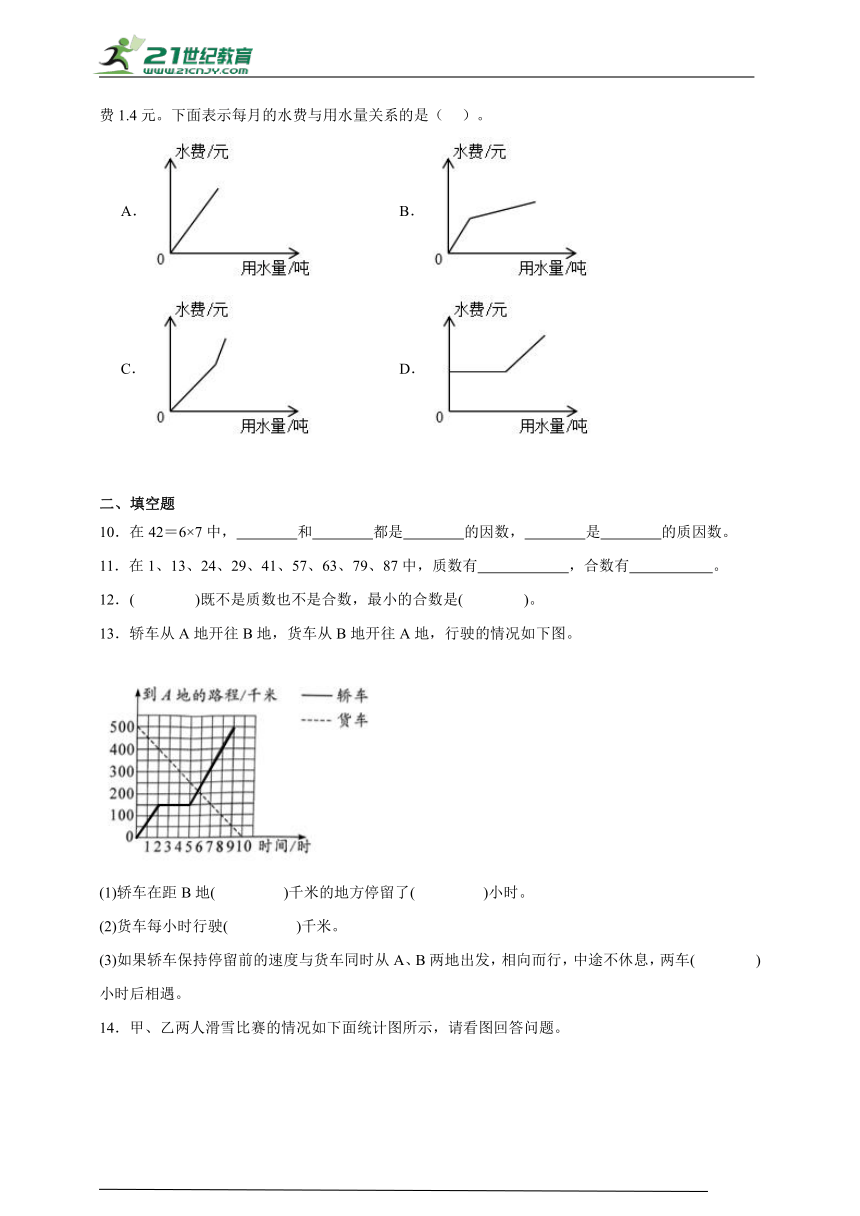
9.自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。下面表示每月的水费与用水量关系的是( )。
A. B.
C. D.
二、填空题
10.在42=6×7中, 和 都是 的因数, 是 的质因数。
11.在1、13、24、29、41、57、63、79、87中,质数有 ,合数有 。
12.( )既不是质数也不是合数,最小的合数是( )。
13.轿车从A地开往B地,货车从B地开往A地,行驶的情况如下图。
(1)轿车在距B地( )千米的地方停留了( )小时。
(2)货车每小时行驶( )千米。
(3)如果轿车保持停留前的速度与货车同时从A、B两地出发,相向而行,中途不休息,两车( )小时后相遇。
14.甲、乙两人滑雪比赛的情况如下面统计图所示,请看图回答问题。
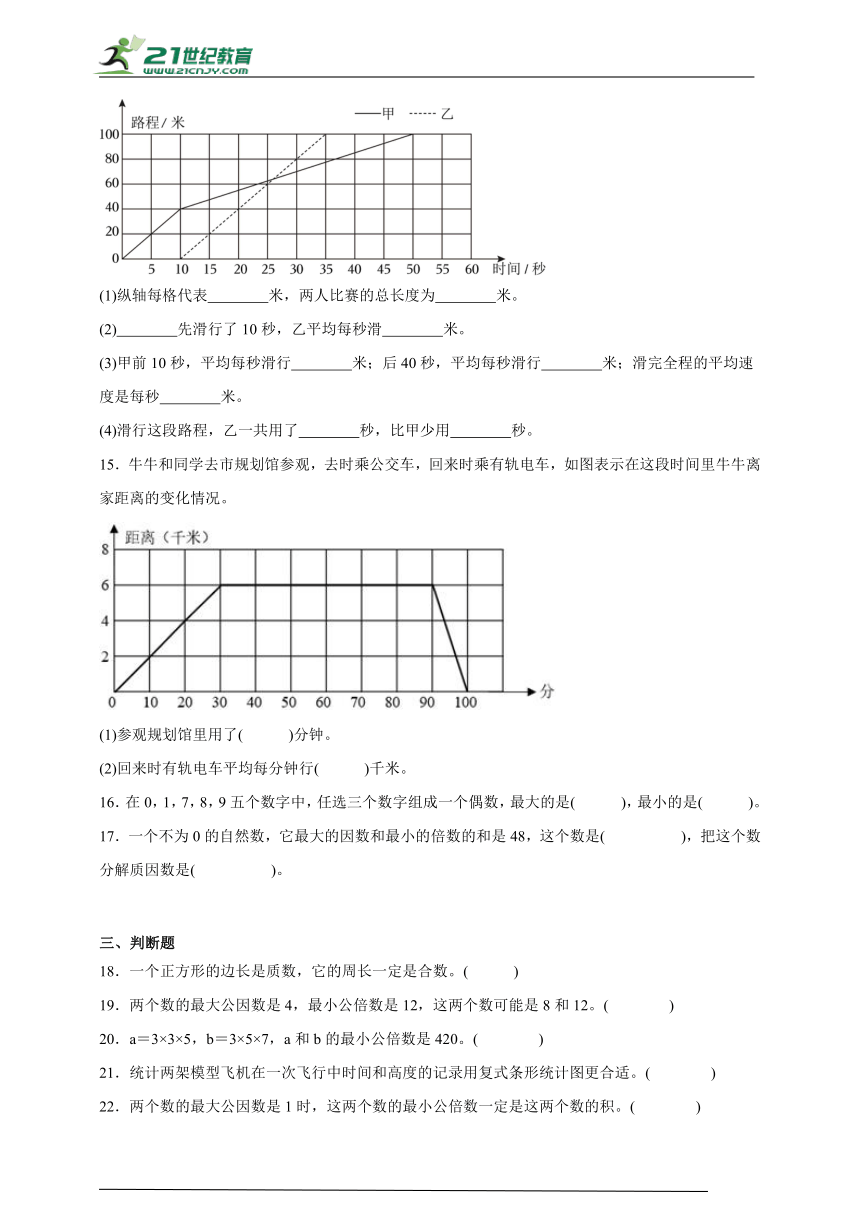
(1)纵轴每格代表 米,两人比赛的总长度为 米。
(2) 先滑行了10秒,乙平均每秒滑 米。
(3)甲前10秒,平均每秒滑行 米;后40秒,平均每秒滑行 米;滑完全程的平均速度是每秒 米。
(4)滑行这段路程,乙一共用了 秒,比甲少用 秒。
15.牛牛和同学去市规划馆参观,去时乘公交车,回来时乘有轨电车,如图表示在这段时间里牛牛离家距离的变化情况。
(1)参观规划馆里用了( )分钟。
(2)回来时有轨电车平均每分钟行( )千米。
16.在0,1,7,8,9五个数字中,任选三个数字组成一个偶数,最大的是( ),最小的是( )。
17.一个不为0的自然数,它最大的因数和最小的倍数的和是48,这个数是( ),把这个数分解质因数是( )。
三、判断题
18.一个正方形的边长是质数,它的周长一定是合数。( )
19.两个数的最大公因数是4,最小公倍数是12,这两个数可能是8和12。( )
20.a=3×3×5,b=3×5×7,a和b的最小公倍数是420。( )
21.统计两架模型飞机在一次飞行中时间和高度的记录用复式条形统计图更合适。( )
22.两个数的最大公因数是1时,这两个数的最小公倍数一定是这两个数的积。( )
四、计算题
23.求下面每组数的最大公因数和最小公倍数。
(16,24)= (13,91)= (12,13)=
[16,24]= [13,91]= [12,13]=
五、作图题
24.把下面的图分割成几个面积最大并且相等的正方形(没有剩余),写出计算过程,并在图中画一画。
六、解答题
25.五(4)班学生为庆祝“六一”儿童节,需要用彩带装饰花篮。如果把如图的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带最长是多少厘米?一共90厘米可以剪成这样的短彩带多少根?
26.下面是利民小学五年级三个社团的人数。
社团 美术 合唱 舞蹈
人数 47 48 49
哪个社团可以分成人数相等的小组(至少分成2组,每个小组至少2人)?为什么?
27.雯雯家打算给卧室的地面铺正方形地砖,要求只铺一种规格的地砖,且铺得既整齐又没有剩余。地面的形状是一个长42分米、宽36分米的长方形,有几种不同规格的正方形地砖可供雯雯家选择?如果选用最大规格的正方形地砖,那么需要多少块?(只考虑地砖的大小,地砖边长为整分米数)
28.一箱苹果,4个4个地拿,还多1个;5个5个地拿,也多1个。这箱苹果至少有多少个?
29.一包饼干,无论平均分给8个小朋友还是10个小朋友,都少3块。这包饼干至少有多少块?
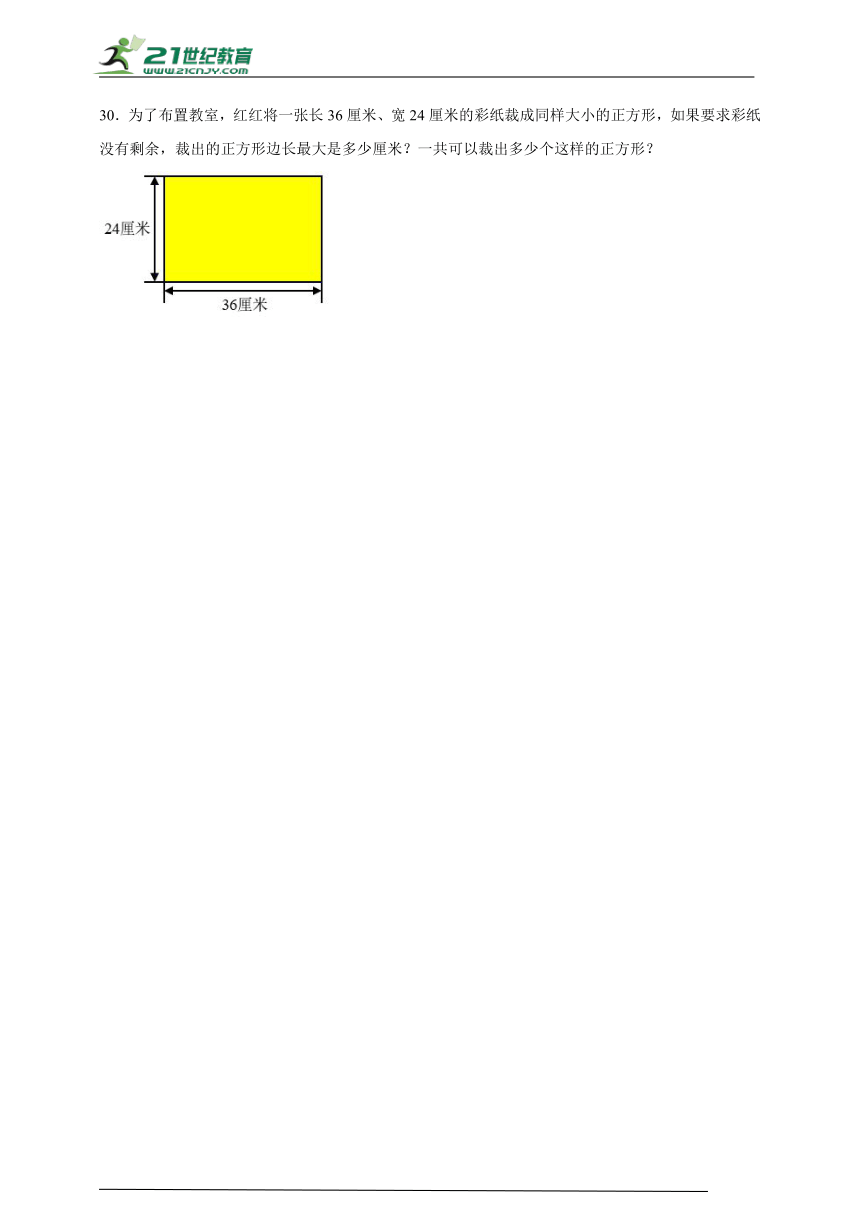
30.为了布置教室,红红将一张长36厘米、宽24厘米的彩纸裁成同样大小的正方形,如果要求彩纸没有剩余,裁出的正方形边长最大是多少厘米?一共可以裁出多少个这样的正方形?
《五年级暑假月考测试卷:第二至三单元(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 B B A A B B B C C
1.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【详解】适合用折线统计图表示的是某电视剧豆瓣评分变化情况。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图各自的特点进行解答。
2.B
【分析】奇数和偶数的运算性质:奇数+奇数=偶数,偶数+奇数=奇数,偶数+偶数=偶数,奇数×偶数=偶数,偶数×偶数=偶数,奇数×奇数=奇数,据此解答。
【详解】由分析得:
A.是非0自然数),奇数的平方是奇数,偶数的平方是偶数,所以结果不一定的奇数,不符合题意;
B.,因为奇数的个数是奇数,所以它们的和一定奇数,符合题意;
C.两个合数相加可能是奇数,也可能是偶数,不符合题意;
D.所有质数的积一定是偶数,不符合题意;
故答案为:B
3.A
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
根据题意,两个连续的自然数中一定有一个奇数和一个偶数,根据“奇数×偶数=偶数”,“奇数+偶数=奇数”,据此判断。
【详解】如:连续自然数1和2;1×2=2,2是偶数;1+2=3,3是奇数;
连续自然数4和5;4×5=20,20是偶数;4+5=9,9是奇数;
所以,两个连续自然数,它们的积一定是偶数,它们的和一定是奇数。
故答案为:A
4.A
【分析】能被2整除的数是偶数,不能被2整除的数是奇数,只有因数1和它本身两个因数的数是质数,除了1和它本身还有其它因数的数叫做合数,由此举例解答即可。
可以用举例法来解答。
【详解】A.假设奇数是3、偶数是4,则3+4=7,和是奇数,故此项不成立。
B.假设两个奇数是3和5,则3+5=8,和是偶数,故此项成立。
C.假设质数是5、合数是9,则5×9=45,积是合数,故此项成立。
D.假设奇数是3、偶数是4,则3×4=12,积是偶数,故此项成立。
故答案为:A
【点睛】此题主要考查的是奇数、偶数、合数、质数含义的灵活应用。
5.B
【分析】先求出原来灯笼之间的间隔数,间隔数60÷3=20(个),题目说共挂了21个,说明起点处也挂了1个灯笼。由每隔3米挂一个灯笼,改为每隔4米挂一个灯笼,不需要移动的灯笼有:间隔为3和4的公倍数处的灯笼以及起点处的一个灯笼。据此解答。
【详解】3和4互质,所以3和4的最小公倍数是:3×4=12。
60÷12=5(个)
5+1=6(个)
共有6个灯笼不要移动。
故答案为:B
6.B
【分析】两数成倍数关系,最大公因数是较小数,据此分析。
【详解】已知m÷n=7,m、n都是不为0的自然数,说明m是n的7倍,那么m和n的最大公因数是n。
故答案为:B
7.B
【分析】条形统计图能很容易看出数量的多少;
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
扇形统计图能反映部分与整体的关系,由此根据情况选择即可。
【详解】在新冠疫情流行期间,采用折线统计图既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
8.C
【分析】在整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;根据变换的队形刚好站两行和1个人,可是在五(1)班学生人数是奇数,分析计算出各个选项队伍中的人数,是偶数的则不可能是五(1)班。
【详解】
A.
5×6=30(人),30是偶数,不符合题意。
B.
3+5×5
=3+25
=28(人)
28是偶数,不符合题意。
C.
3+4×7
=3+28
=31(人)
31是奇数,符合题意。
D.
4+4×6
=4×24
=28(人)
28是偶数,不符合题意。
开幕式表演队形中,五(1)班的队形可能是。
故答案为:C
9.C
【分析】由于分段计费,所以图像是折线。每户每月用水量不超过15每吨价格为0.5元,超过15吨时超过部分每吨收费1.4元。所以15吨以内的总价和数量的折线上升较慢,超过15吨总价和数量的折线上升较快,据此选择即可。
【详解】A.,因为图像是一条直线,没有表示出超过15吨后水费与用水量的关系,不符合题意;
B.,没有准确表示超过15吨后水费和用水量的关系,不符合题意;
C.,能表示每月的水费与用水量关系,符合题意;
D.,图中没有表示出15吨以内水费与用水量的关系,不符合题意。
自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。表示每月的水费与用水量关系的是。
故答案为:C
【点睛】本题考查的目的是理解掌握折线统计图的特征及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10. 6 7 42 7 42
【分析】若整数a能够被b整除,a叫做b的倍数,b就叫做a的因数,因数与倍数是相互依存的;以及质因数的意义:如果一个整数的因数是质数,为质数的因数叫做质因数;据此解答。
【详解】在42=6×7中,6和7都是42的因数,7是42的质因数。
【点睛】本题主要考查因数与倍数的意义,注意因数与倍数是相互依存的。
11. 13、29、41、79 24、57、63、87
【分析】根据质数和合数的定义:一个自然数。如果只有1和它本身两个因数,这样的数叫做质数;如果除了1和它本身还有别的因数,这样的数叫做合数;1既不是质数,也不是合数;据此填空即可。
【详解】因数只有1和它本身两个因数的数有:13、29、41、79;因数中除了1和它本身还有别的因数的数有:24、57、63、87;1既不是质数,也不是合数。
则在1、13、24、29、41、57、63、79、87中,质数有13、29、41、79,合数有24、57、63、87。
12. 1 4
【分析】质数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数。合数指自然数中除了能被1和本身整除外,还能被其他数整除的数(0除外);而1既不属于质数也不属于合数。最小的合数是4。据此解答。
【详解】(1)既不是质数也不是合数,最小的合数是(4)。
【点睛】掌握质数、合数的概念是解答本题的关键。
13.(1) 350 3
(2)50
(3)4
【分析】(1)由图可知,轿车从2到5小时之间停留了,停留时间为(5-2)小时;停留时已经行驶了150千米,与B地相距的距离为(500-150)千米。
(2)货车从B地开往A地,距离是500千米,行驶时间是10小时,根据速度=路程÷时间,代入相应数值计算即可解答。
(3)由图可知,轿车2小时内行驶了150千米,根据速度=路程÷时间,计算出轿车停留前的速度;货车的速度已知,根据相遇时间=两地的距离÷两车的速度之和,代入相应数值计算,据此解答。
【详解】(1)5-2=3(小时)
500-150=350(千米)
因此轿车在距B地350千米的地方停留了3小时。
(2)500÷10=50(千米/时)
因此货车每小时行驶50千米。
(3)150÷2=75(千米/时)
500÷(50+75)
=500÷125
=4(小时)
因此两车4小时后相遇。
14.(1) 20 100
(2) 甲 4
(3) 4 1.5 2
(4) 25 25
【分析】(1)从纵轴上的数,找出每格代表的米数,看折线图的最顶端对应的纵轴数据,可知两人比赛的总长度;
(2)甲起点的横轴数据为0,乙起点的横轴数据为10,可见甲比乙先滑行10秒,用比赛总长度除以乙滑行的时间,即乙平均每秒滑行的米数;
(3)甲前10秒滑行40米,后40秒滑行米,用行的路程除对应的时间,可以求出前10秒的平均速度、后40秒的平均速度以及全程的平均速度;
(4)从横轴上看乙从第10秒开始滑行,到第35秒结束,用结束时间减开始时间,就是他滑行的时间,用甲滑行的时间减乙滑行的时间,求出乙比甲少用多少时间。
【详解】(1)纵轴每格代表20米,两人比赛的总长度为100米。
(2)(100÷35) 10
=100÷25
=4(米秒)
甲先滑行了10秒;乙平均每秒滑4米。
(3)40÷10=4(米秒)
(100 40)÷40
=60÷40
=1.5(米秒)
100÷50=2(米秒)
甲前10秒,平均每秒滑行4米;平均每秒滑行1.5米;滑完全程的平均速度是每秒2米。
(4)35-10=25(秒)
50-25=25(秒)
乙一共用了25秒;比甲少用25秒。
15.(1)60
(2)0.6
【分析】(1)观察图中路程和时间的变化,牛牛和同学去市规划馆参观,分钟这段时间在乘公交车,分钟这段时间路程不变,说明牛牛和同学正在市规划馆里面参观。
(2)分钟这段时间里,说明牛牛和同学乘有轨电车回到家中,路程是6千米,用路程除以经过的时间,求出有轨电车平均每分钟行的千米数。
【详解】(1)(分钟)
所以参观规划馆里用了60分钟。
(2)回来时有轨电车用时:(分钟)
(千米)
所以回来时有轨电车平均每分钟行0.6千米。
【点睛】本题考查行程问题、折线统计图,解答本题的关键是看懂图形中路程、时间的变化对应的是实际生活中发生的哪一种具体情况的变化。
16. 980 108
【分析】能被2整除的数叫作偶数,即末尾是2、4、6、8、0的数是偶数。根据数的比较数的比较大小,先确定最高位,再确定个位上的数,最后再确定中间的数。
【详解】这五个数中最大的是9,末尾可以是0或者8,则最大的数是980;
最小的数是1,则最小的数108。
则任选三个数字组成一个偶数,最大的是980,最小的是108。
17. 24 24=2×2×2×3
【分析】这个数最大的因数和最小的倍数的和是48,根据“一个数的最大因数和最小倍数都是它本身”,可用48÷2求出这个数;再把求出的数写成几个质数相乘的形式即为分解质因数。
【详解】由分析可得:
这个数为:48÷2=24
分解质因数:24=2×2×2×3
综上所述,一个不为0的自然数,它最大的因数和最小的倍数的和是48,这个数是24,把这个数分解质因数是24=2×2×2×3。
【点睛】此题主要考查因数与倍数的意义及分解质因数的方法,明确一个数的最大因数和最小倍数都是它本身是解题的关键。
18.√
【分析】根据质数:只有1和它本身两个因数的数叫做质数;合数:除了1和它本身外,还有其他因数的数叫合数;。
【详解】由题意可知,正方形的周长除了1和它本身外,还有4、边长、2、边长的2倍这些因数,所以正方形的周长一定是合数;原题说法正确。
故答案为:√
19.×
【分析】最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此可设这两个数分别是4x,4y,x和y互质,且4xy=12,据此求出xy的积,进而推出x和y的值,最后推出这两个数。据此解答。
【详解】设这两个数分别是4x,4y,
4xy=12
解:4xy÷4=12÷4
xy=3
3=1×3
1×4=4
3×4=12
两个数的最大公因数是4,最小公倍数是12,这两个数是4和12。原题干说法错误。
故答案为:×
【点睛】本题考查了最大公因数和最小公倍数的认识和应用。
20.×
【分析】全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。
【详解】3×3×5×7=315
a=3×3×5,b=3×5×7,a和b的最小公倍数是315,原题说法错误。
故答案为:×
21.×
【分析】条形统计图可以直观地显示数量的多少。折线统计图除了显示数量的多少,还可以清楚地反应数量的增减变化情况。根据各种统计图的特点,选择合适的统计图,据此解答。
【详解】由分析得:统计两架模型飞机在一次飞行中时间和高度的记录用复式折线统计图更合适,所以原题说法错误。
故答案为:×
22.√
【分析】当两个数的最大公因数是1时,说明这两个数是互质数,那么它们的最小公倍数是这两个数的乘积,据此判断。
【详解】如:3和5是互质数,它们的最大公因数是1,最小公倍数是3×5=15。
因此当两个数的最大公因数是1,这两个数的最小公倍数一定是这两个数的积,原题干的说法是正确的。
故答案为:√
23.8;13;1;
48;91;156
【分析】求两个数的最大公因数和最小公倍数,如果两个数互质,则这两个数的最大公因数是1,最小公倍数是它们的乘积;
如果两个数是倍数关系,则这两个数的最大公因数是其中较小的数,最小公倍数是其中较大的数;
如果两个数既不互质,也不是倍数关系,则先把两个数分别分解质因数,这两个数的最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此解答。
【详解】16=2×2×2×2
24=2×2×2×3
16和24的最大公因数:2×2×2=8
16和24的最小公倍数:2×2×2×2×3=48
91÷13=7
91和13是倍数关系,
91和13的最大公因数是13,最小公倍数是91;
12和13互质,
12×13=156
12和13的最大公因数是1,最小公倍数是156。
24.见详解
【分析】分别数出整个长方形的长和宽,求出长和宽的最大公因数就是分割成的最大正方形的边长,全部共有的质因数相乘的积就是这几个数的最大公因数。据此确定正方形的边长,作图即可。
【详解】长方形的长16cm,宽12cm。
16=2×2×2×2
12=2×2×3
2×2=4(cm)
正方形边长最长是4cm,作图如下:
25.30厘米;3根
【分析】把90厘米、60厘米长的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带要最长,就是求90和60的最大公因数。把90、60分解质因数后,把公有的相同质因数乘起来就是最大公因数。就是它们每根短彩带最长是多少厘米。再看90里面有几个这样的最大公因数,即是90厘米一共可以剪成这样的短彩带的总根数。
【详解】
60和90的最大公因数是。
(根
答:每根短彩带最长是30厘米,一共90厘米可以剪成这样的短彩带3根。
26.合唱社团和舞蹈社团;48和49是合数
【分析】根据质数和合数的特点,除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数,如果社团人数是质数,因数只有1和它本身,不可以平均分成人数相同的小组;如果社团人数是合数,则可平均分成人数相同的小组。据此解答即可。
【详解】班级人数是质数的是47,班级人数是合数的有48、49。
答:合唱社团和舞蹈社团可以平均分成人数相同的小组,因为48和49是合数。
27.4;42块
【分析】首先求出42和36的公因数,它们之间有几个公因数就有几种不同规格的正方形地砖可选择;地面是一个长方形,用长和宽分别除以最大公因数,可得长能放的块数和宽能放的块数,最后相乘,就是需要砖的块数。
【详解】42的因数有:1,2,3,6,7,14,21,42
36的因数有:1,2,3,4,6,9,12,18,36
42和36的公因数有:1,2,3,6,有4个公因数。
42和36的最大公因数是:6
42÷6=7(块)
36÷6=6(块)
6×7=42(块)
答:有4种不同规格的正方形地砖可供雯雯家选择。如果选用最大规格的正方形地砖,那么需要42块。
【点睛】本题是一道关于最大公因数应用题目,注意求最大公因数的方法和计算的正确性。
28.21个
【分析】由题可知,4个4个地拿,还多1个;5个5个地拿,也多1个,说明这箱苹果的个数至少比4和5的最小公倍数多1,求出4和5的最小公倍数,加上1即可。
【详解】4×5=20
20+1=21(个)
答:这箱苹果至少有21个。
29.37块
【分析】如果给这包饼干的块数加上3,就是8和10的公倍数;则可以先求出8和10的最小公倍数,减去3块就是这包饼干至少有多少块。
【详解】10=2×5
8=2×2×2
所以8和10的最小公倍数是:2×2×2×5=40
所以这包饼干至少有:40-3=37(块)
答:这包饼干至少有37块。
30.12厘米;6个
【分析】求出彩纸长和宽的最大公因数,就是裁出的最大正方形的边长;根据正方形面积=边长×边长,长方形面积=长×宽,分别求出彩纸和正方形的面积,用长方形面积÷正方形面积=裁出的正方形的个数,据此列式解答。
【详解】36=2×2×3×3
24=2×2×2×3
2×2×3=12(厘米)
36×24÷(12×12)
=864÷144
=6(个)
答:裁出的正方形边长最大是12厘米,一共可以裁出6个这样的正方形。
【点睛】关键是掌握并灵活运用长方形和正方形的面积公式,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面的资料信息中,适合用折线统计图表示的是( )。
A.甜品店一天卖出各种奶茶的数量
B.某电视剧豆瓣评分变化情况
C.爸爸手机里各APP占用内存情况
2.下面算式的结果一定是奇数的是( )。
A.是非0自然数) B.
C.两个合数相加 D.所有质数的乘积
3.两个连续自然数,它们的积一定是( ),它们的和一定是( )。
A.偶数;奇数 B.奇数;合数 C.奇数;质数 D. 偶数;质数
4.下列等式不成立的是( )。
A.奇数+偶数=偶数 B.奇数+奇数=偶数
C.质数×合数=合数 D.偶数×奇数=偶数
5.在一条60米的长廊的一侧,每隔3米挂一个红灯笼,共挂了21个。现在要将每两个灯笼之间的间隔改为4米,共有( )个灯笼不要移动。
A.5 B.6 C.7 D.8
6.已知m÷n=7,m、n都是不为0的自然数,那么m和n的最大公因数是( )。
A.m B.n C.7 D.1
7.在新冠疫情流行期间,采用( )既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
A.条形统计图 B.折线统计图 C.扇形统计图 D.三种都可以
8.运动会开幕式上,五(1)班入场队列如下图。所有人入场后都参加了开幕式表演,表演时变换了队形。下面四个开幕式表演队形中,五(1)班的队形可能是( )。
A. B. C. D.
9.自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。下面表示每月的水费与用水量关系的是( )。
A. B.
C. D.
二、填空题
10.在42=6×7中, 和 都是 的因数, 是 的质因数。
11.在1、13、24、29、41、57、63、79、87中,质数有 ,合数有 。
12.( )既不是质数也不是合数,最小的合数是( )。
13.轿车从A地开往B地,货车从B地开往A地,行驶的情况如下图。
(1)轿车在距B地( )千米的地方停留了( )小时。
(2)货车每小时行驶( )千米。
(3)如果轿车保持停留前的速度与货车同时从A、B两地出发,相向而行,中途不休息,两车( )小时后相遇。
14.甲、乙两人滑雪比赛的情况如下面统计图所示,请看图回答问题。
(1)纵轴每格代表 米,两人比赛的总长度为 米。
(2) 先滑行了10秒,乙平均每秒滑 米。
(3)甲前10秒,平均每秒滑行 米;后40秒,平均每秒滑行 米;滑完全程的平均速度是每秒 米。
(4)滑行这段路程,乙一共用了 秒,比甲少用 秒。
15.牛牛和同学去市规划馆参观,去时乘公交车,回来时乘有轨电车,如图表示在这段时间里牛牛离家距离的变化情况。
(1)参观规划馆里用了( )分钟。
(2)回来时有轨电车平均每分钟行( )千米。
16.在0,1,7,8,9五个数字中,任选三个数字组成一个偶数,最大的是( ),最小的是( )。
17.一个不为0的自然数,它最大的因数和最小的倍数的和是48,这个数是( ),把这个数分解质因数是( )。
三、判断题
18.一个正方形的边长是质数,它的周长一定是合数。( )
19.两个数的最大公因数是4,最小公倍数是12,这两个数可能是8和12。( )
20.a=3×3×5,b=3×5×7,a和b的最小公倍数是420。( )
21.统计两架模型飞机在一次飞行中时间和高度的记录用复式条形统计图更合适。( )
22.两个数的最大公因数是1时,这两个数的最小公倍数一定是这两个数的积。( )
四、计算题
23.求下面每组数的最大公因数和最小公倍数。
(16,24)= (13,91)= (12,13)=
[16,24]= [13,91]= [12,13]=
五、作图题
24.把下面的图分割成几个面积最大并且相等的正方形(没有剩余),写出计算过程,并在图中画一画。
六、解答题
25.五(4)班学生为庆祝“六一”儿童节,需要用彩带装饰花篮。如果把如图的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带最长是多少厘米?一共90厘米可以剪成这样的短彩带多少根?
26.下面是利民小学五年级三个社团的人数。
社团 美术 合唱 舞蹈
人数 47 48 49
哪个社团可以分成人数相等的小组(至少分成2组,每个小组至少2人)?为什么?
27.雯雯家打算给卧室的地面铺正方形地砖,要求只铺一种规格的地砖,且铺得既整齐又没有剩余。地面的形状是一个长42分米、宽36分米的长方形,有几种不同规格的正方形地砖可供雯雯家选择?如果选用最大规格的正方形地砖,那么需要多少块?(只考虑地砖的大小,地砖边长为整分米数)
28.一箱苹果,4个4个地拿,还多1个;5个5个地拿,也多1个。这箱苹果至少有多少个?
29.一包饼干,无论平均分给8个小朋友还是10个小朋友,都少3块。这包饼干至少有多少块?
30.为了布置教室,红红将一张长36厘米、宽24厘米的彩纸裁成同样大小的正方形,如果要求彩纸没有剩余,裁出的正方形边长最大是多少厘米?一共可以裁出多少个这样的正方形?
《五年级暑假月考测试卷:第二至三单元(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 B B A A B B B C C
1.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【详解】适合用折线统计图表示的是某电视剧豆瓣评分变化情况。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图各自的特点进行解答。
2.B
【分析】奇数和偶数的运算性质:奇数+奇数=偶数,偶数+奇数=奇数,偶数+偶数=偶数,奇数×偶数=偶数,偶数×偶数=偶数,奇数×奇数=奇数,据此解答。
【详解】由分析得:
A.是非0自然数),奇数的平方是奇数,偶数的平方是偶数,所以结果不一定的奇数,不符合题意;
B.,因为奇数的个数是奇数,所以它们的和一定奇数,符合题意;
C.两个合数相加可能是奇数,也可能是偶数,不符合题意;
D.所有质数的积一定是偶数,不符合题意;
故答案为:B
3.A
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
根据题意,两个连续的自然数中一定有一个奇数和一个偶数,根据“奇数×偶数=偶数”,“奇数+偶数=奇数”,据此判断。
【详解】如:连续自然数1和2;1×2=2,2是偶数;1+2=3,3是奇数;
连续自然数4和5;4×5=20,20是偶数;4+5=9,9是奇数;
所以,两个连续自然数,它们的积一定是偶数,它们的和一定是奇数。
故答案为:A
4.A
【分析】能被2整除的数是偶数,不能被2整除的数是奇数,只有因数1和它本身两个因数的数是质数,除了1和它本身还有其它因数的数叫做合数,由此举例解答即可。
可以用举例法来解答。
【详解】A.假设奇数是3、偶数是4,则3+4=7,和是奇数,故此项不成立。
B.假设两个奇数是3和5,则3+5=8,和是偶数,故此项成立。
C.假设质数是5、合数是9,则5×9=45,积是合数,故此项成立。
D.假设奇数是3、偶数是4,则3×4=12,积是偶数,故此项成立。
故答案为:A
【点睛】此题主要考查的是奇数、偶数、合数、质数含义的灵活应用。
5.B
【分析】先求出原来灯笼之间的间隔数,间隔数60÷3=20(个),题目说共挂了21个,说明起点处也挂了1个灯笼。由每隔3米挂一个灯笼,改为每隔4米挂一个灯笼,不需要移动的灯笼有:间隔为3和4的公倍数处的灯笼以及起点处的一个灯笼。据此解答。
【详解】3和4互质,所以3和4的最小公倍数是:3×4=12。
60÷12=5(个)
5+1=6(个)
共有6个灯笼不要移动。
故答案为:B
6.B
【分析】两数成倍数关系,最大公因数是较小数,据此分析。
【详解】已知m÷n=7,m、n都是不为0的自然数,说明m是n的7倍,那么m和n的最大公因数是n。
故答案为:B
7.B
【分析】条形统计图能很容易看出数量的多少;
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
扇形统计图能反映部分与整体的关系,由此根据情况选择即可。
【详解】在新冠疫情流行期间,采用折线统计图既能反映每天病患的人数,又能反映疫情变化的情况和趋势。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
8.C
【分析】在整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数;根据变换的队形刚好站两行和1个人,可是在五(1)班学生人数是奇数,分析计算出各个选项队伍中的人数,是偶数的则不可能是五(1)班。
【详解】
A.
5×6=30(人),30是偶数,不符合题意。
B.
3+5×5
=3+25
=28(人)
28是偶数,不符合题意。
C.
3+4×7
=3+28
=31(人)
31是奇数,符合题意。
D.
4+4×6
=4×24
=28(人)
28是偶数,不符合题意。
开幕式表演队形中,五(1)班的队形可能是。
故答案为:C
9.C
【分析】由于分段计费,所以图像是折线。每户每月用水量不超过15每吨价格为0.5元,超过15吨时超过部分每吨收费1.4元。所以15吨以内的总价和数量的折线上升较慢,超过15吨总价和数量的折线上升较快,据此选择即可。
【详解】A.,因为图像是一条直线,没有表示出超过15吨后水费与用水量的关系,不符合题意;
B.,没有准确表示超过15吨后水费和用水量的关系,不符合题意;
C.,能表示每月的水费与用水量关系,符合题意;
D.,图中没有表示出15吨以内水费与用水量的关系,不符合题意。
自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。表示每月的水费与用水量关系的是。
故答案为:C
【点睛】本题考查的目的是理解掌握折线统计图的特征及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10. 6 7 42 7 42
【分析】若整数a能够被b整除,a叫做b的倍数,b就叫做a的因数,因数与倍数是相互依存的;以及质因数的意义:如果一个整数的因数是质数,为质数的因数叫做质因数;据此解答。
【详解】在42=6×7中,6和7都是42的因数,7是42的质因数。
【点睛】本题主要考查因数与倍数的意义,注意因数与倍数是相互依存的。
11. 13、29、41、79 24、57、63、87
【分析】根据质数和合数的定义:一个自然数。如果只有1和它本身两个因数,这样的数叫做质数;如果除了1和它本身还有别的因数,这样的数叫做合数;1既不是质数,也不是合数;据此填空即可。
【详解】因数只有1和它本身两个因数的数有:13、29、41、79;因数中除了1和它本身还有别的因数的数有:24、57、63、87;1既不是质数,也不是合数。
则在1、13、24、29、41、57、63、79、87中,质数有13、29、41、79,合数有24、57、63、87。
12. 1 4
【分析】质数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数。合数指自然数中除了能被1和本身整除外,还能被其他数整除的数(0除外);而1既不属于质数也不属于合数。最小的合数是4。据此解答。
【详解】(1)既不是质数也不是合数,最小的合数是(4)。
【点睛】掌握质数、合数的概念是解答本题的关键。
13.(1) 350 3
(2)50
(3)4
【分析】(1)由图可知,轿车从2到5小时之间停留了,停留时间为(5-2)小时;停留时已经行驶了150千米,与B地相距的距离为(500-150)千米。
(2)货车从B地开往A地,距离是500千米,行驶时间是10小时,根据速度=路程÷时间,代入相应数值计算即可解答。
(3)由图可知,轿车2小时内行驶了150千米,根据速度=路程÷时间,计算出轿车停留前的速度;货车的速度已知,根据相遇时间=两地的距离÷两车的速度之和,代入相应数值计算,据此解答。
【详解】(1)5-2=3(小时)
500-150=350(千米)
因此轿车在距B地350千米的地方停留了3小时。
(2)500÷10=50(千米/时)
因此货车每小时行驶50千米。
(3)150÷2=75(千米/时)
500÷(50+75)
=500÷125
=4(小时)
因此两车4小时后相遇。
14.(1) 20 100
(2) 甲 4
(3) 4 1.5 2
(4) 25 25
【分析】(1)从纵轴上的数,找出每格代表的米数,看折线图的最顶端对应的纵轴数据,可知两人比赛的总长度;
(2)甲起点的横轴数据为0,乙起点的横轴数据为10,可见甲比乙先滑行10秒,用比赛总长度除以乙滑行的时间,即乙平均每秒滑行的米数;
(3)甲前10秒滑行40米,后40秒滑行米,用行的路程除对应的时间,可以求出前10秒的平均速度、后40秒的平均速度以及全程的平均速度;
(4)从横轴上看乙从第10秒开始滑行,到第35秒结束,用结束时间减开始时间,就是他滑行的时间,用甲滑行的时间减乙滑行的时间,求出乙比甲少用多少时间。
【详解】(1)纵轴每格代表20米,两人比赛的总长度为100米。
(2)(100÷35) 10
=100÷25
=4(米秒)
甲先滑行了10秒;乙平均每秒滑4米。
(3)40÷10=4(米秒)
(100 40)÷40
=60÷40
=1.5(米秒)
100÷50=2(米秒)
甲前10秒,平均每秒滑行4米;平均每秒滑行1.5米;滑完全程的平均速度是每秒2米。
(4)35-10=25(秒)
50-25=25(秒)
乙一共用了25秒;比甲少用25秒。
15.(1)60
(2)0.6
【分析】(1)观察图中路程和时间的变化,牛牛和同学去市规划馆参观,分钟这段时间在乘公交车,分钟这段时间路程不变,说明牛牛和同学正在市规划馆里面参观。
(2)分钟这段时间里,说明牛牛和同学乘有轨电车回到家中,路程是6千米,用路程除以经过的时间,求出有轨电车平均每分钟行的千米数。
【详解】(1)(分钟)
所以参观规划馆里用了60分钟。
(2)回来时有轨电车用时:(分钟)
(千米)
所以回来时有轨电车平均每分钟行0.6千米。
【点睛】本题考查行程问题、折线统计图,解答本题的关键是看懂图形中路程、时间的变化对应的是实际生活中发生的哪一种具体情况的变化。
16. 980 108
【分析】能被2整除的数叫作偶数,即末尾是2、4、6、8、0的数是偶数。根据数的比较数的比较大小,先确定最高位,再确定个位上的数,最后再确定中间的数。
【详解】这五个数中最大的是9,末尾可以是0或者8,则最大的数是980;
最小的数是1,则最小的数108。
则任选三个数字组成一个偶数,最大的是980,最小的是108。
17. 24 24=2×2×2×3
【分析】这个数最大的因数和最小的倍数的和是48,根据“一个数的最大因数和最小倍数都是它本身”,可用48÷2求出这个数;再把求出的数写成几个质数相乘的形式即为分解质因数。
【详解】由分析可得:
这个数为:48÷2=24
分解质因数:24=2×2×2×3
综上所述,一个不为0的自然数,它最大的因数和最小的倍数的和是48,这个数是24,把这个数分解质因数是24=2×2×2×3。
【点睛】此题主要考查因数与倍数的意义及分解质因数的方法,明确一个数的最大因数和最小倍数都是它本身是解题的关键。
18.√
【分析】根据质数:只有1和它本身两个因数的数叫做质数;合数:除了1和它本身外,还有其他因数的数叫合数;。
【详解】由题意可知,正方形的周长除了1和它本身外,还有4、边长、2、边长的2倍这些因数,所以正方形的周长一定是合数;原题说法正确。
故答案为:√
19.×
【分析】最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此可设这两个数分别是4x,4y,x和y互质,且4xy=12,据此求出xy的积,进而推出x和y的值,最后推出这两个数。据此解答。
【详解】设这两个数分别是4x,4y,
4xy=12
解:4xy÷4=12÷4
xy=3
3=1×3
1×4=4
3×4=12
两个数的最大公因数是4,最小公倍数是12,这两个数是4和12。原题干说法错误。
故答案为:×
【点睛】本题考查了最大公因数和最小公倍数的认识和应用。
20.×
【分析】全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。
【详解】3×3×5×7=315
a=3×3×5,b=3×5×7,a和b的最小公倍数是315,原题说法错误。
故答案为:×
21.×
【分析】条形统计图可以直观地显示数量的多少。折线统计图除了显示数量的多少,还可以清楚地反应数量的增减变化情况。根据各种统计图的特点,选择合适的统计图,据此解答。
【详解】由分析得:统计两架模型飞机在一次飞行中时间和高度的记录用复式折线统计图更合适,所以原题说法错误。
故答案为:×
22.√
【分析】当两个数的最大公因数是1时,说明这两个数是互质数,那么它们的最小公倍数是这两个数的乘积,据此判断。
【详解】如:3和5是互质数,它们的最大公因数是1,最小公倍数是3×5=15。
因此当两个数的最大公因数是1,这两个数的最小公倍数一定是这两个数的积,原题干的说法是正确的。
故答案为:√
23.8;13;1;
48;91;156
【分析】求两个数的最大公因数和最小公倍数,如果两个数互质,则这两个数的最大公因数是1,最小公倍数是它们的乘积;
如果两个数是倍数关系,则这两个数的最大公因数是其中较小的数,最小公倍数是其中较大的数;
如果两个数既不互质,也不是倍数关系,则先把两个数分别分解质因数,这两个数的最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此解答。
【详解】16=2×2×2×2
24=2×2×2×3
16和24的最大公因数:2×2×2=8
16和24的最小公倍数:2×2×2×2×3=48
91÷13=7
91和13是倍数关系,
91和13的最大公因数是13,最小公倍数是91;
12和13互质,
12×13=156
12和13的最大公因数是1,最小公倍数是156。
24.见详解
【分析】分别数出整个长方形的长和宽,求出长和宽的最大公因数就是分割成的最大正方形的边长,全部共有的质因数相乘的积就是这几个数的最大公因数。据此确定正方形的边长,作图即可。
【详解】长方形的长16cm,宽12cm。
16=2×2×2×2
12=2×2×3
2×2=4(cm)
正方形边长最长是4cm,作图如下:
25.30厘米;3根
【分析】把90厘米、60厘米长的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带要最长,就是求90和60的最大公因数。把90、60分解质因数后,把公有的相同质因数乘起来就是最大公因数。就是它们每根短彩带最长是多少厘米。再看90里面有几个这样的最大公因数,即是90厘米一共可以剪成这样的短彩带的总根数。
【详解】
60和90的最大公因数是。
(根
答:每根短彩带最长是30厘米,一共90厘米可以剪成这样的短彩带3根。
26.合唱社团和舞蹈社团;48和49是合数
【分析】根据质数和合数的特点,除了1和它本身以外不再有其他因数,这样的数叫质数;除了1和它本身以外还有其他因数,这样的数叫合数,如果社团人数是质数,因数只有1和它本身,不可以平均分成人数相同的小组;如果社团人数是合数,则可平均分成人数相同的小组。据此解答即可。
【详解】班级人数是质数的是47,班级人数是合数的有48、49。
答:合唱社团和舞蹈社团可以平均分成人数相同的小组,因为48和49是合数。
27.4;42块
【分析】首先求出42和36的公因数,它们之间有几个公因数就有几种不同规格的正方形地砖可选择;地面是一个长方形,用长和宽分别除以最大公因数,可得长能放的块数和宽能放的块数,最后相乘,就是需要砖的块数。
【详解】42的因数有:1,2,3,6,7,14,21,42
36的因数有:1,2,3,4,6,9,12,18,36
42和36的公因数有:1,2,3,6,有4个公因数。
42和36的最大公因数是:6
42÷6=7(块)
36÷6=6(块)
6×7=42(块)
答:有4种不同规格的正方形地砖可供雯雯家选择。如果选用最大规格的正方形地砖,那么需要42块。
【点睛】本题是一道关于最大公因数应用题目,注意求最大公因数的方法和计算的正确性。
28.21个
【分析】由题可知,4个4个地拿,还多1个;5个5个地拿,也多1个,说明这箱苹果的个数至少比4和5的最小公倍数多1,求出4和5的最小公倍数,加上1即可。
【详解】4×5=20
20+1=21(个)
答:这箱苹果至少有21个。
29.37块
【分析】如果给这包饼干的块数加上3,就是8和10的公倍数;则可以先求出8和10的最小公倍数,减去3块就是这包饼干至少有多少块。
【详解】10=2×5
8=2×2×2
所以8和10的最小公倍数是:2×2×2×5=40
所以这包饼干至少有:40-3=37(块)
答:这包饼干至少有37块。
30.12厘米;6个
【分析】求出彩纸长和宽的最大公因数,就是裁出的最大正方形的边长;根据正方形面积=边长×边长,长方形面积=长×宽,分别求出彩纸和正方形的面积,用长方形面积÷正方形面积=裁出的正方形的个数,据此列式解答。
【详解】36=2×2×3×3
24=2×2×2×3
2×2×3=12(厘米)
36×24÷(12×12)
=864÷144
=6(个)
答:裁出的正方形边长最大是12厘米,一共可以裁出6个这样的正方形。
【点睛】关键是掌握并灵活运用长方形和正方形的面积公式,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
