人教版数学七年级上册 6.2.2 线段的比较与运算-课件(36张PPT)
文档属性
| 名称 | 人教版数学七年级上册 6.2.2 线段的比较与运算-课件(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 28.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 22:28:42 | ||
图片预览





文档简介
(共36张PPT)
6.2.2
线段的比较与运算
第6章 几何图形初步
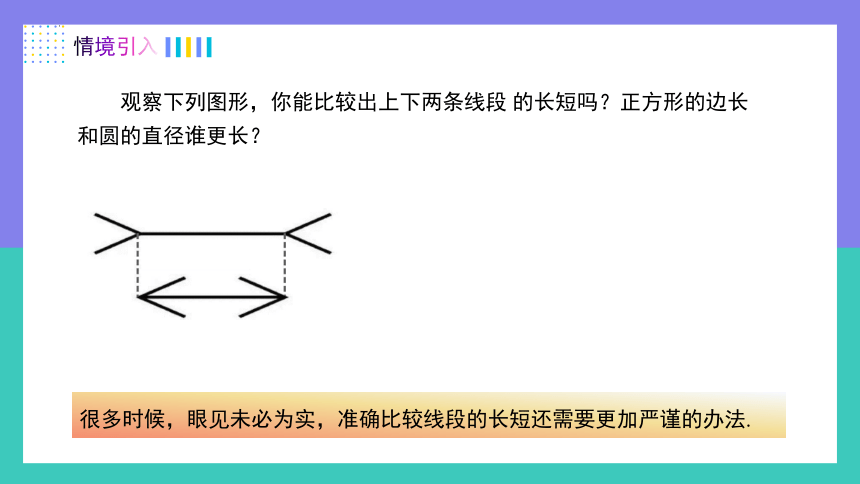
情境引入
很多时候,眼见未必为实,准确比较线段的长短还需要更加严谨的办法.
观察下列图形,你能比较出上下两条线段 的长短吗?正方形的边长和圆的直径谁更长?
新知探究
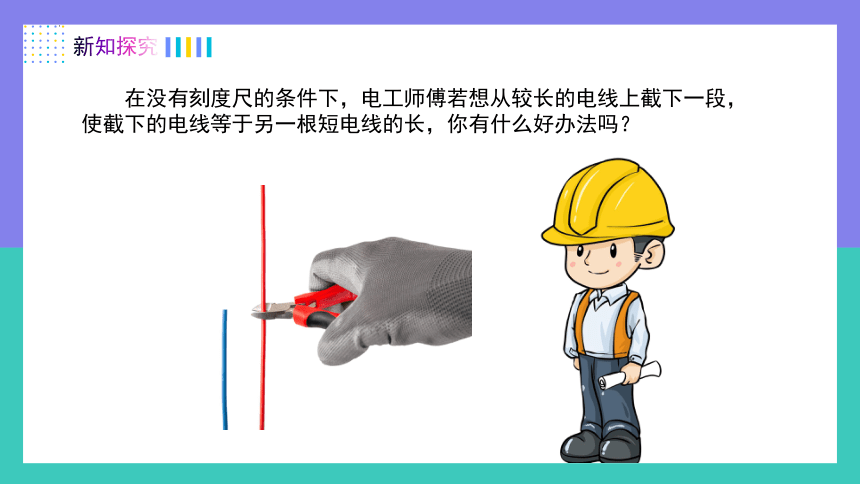
在没有刻度尺的条件下,电工师傅若想从较长的电线上截下一段,使截下的电线等于另一根短电线的长,你有什么好办法吗?
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
思考:
新知探究
新知探究
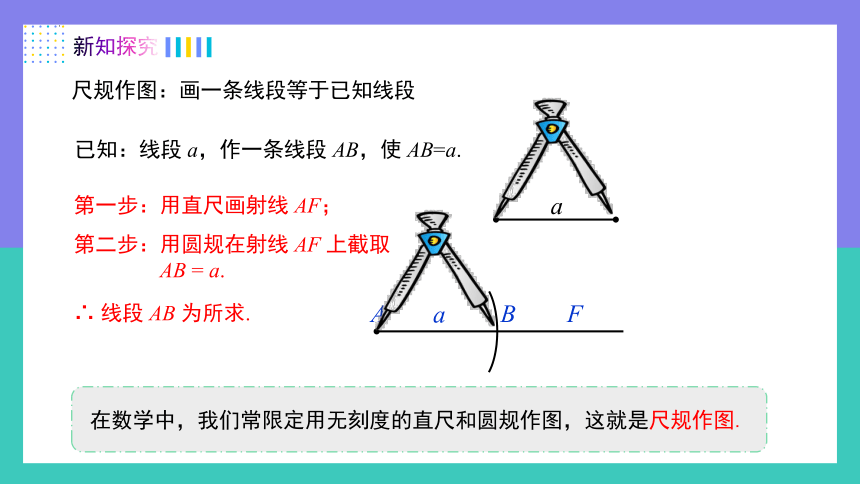
尺规作图:画一条线段等于已知线段
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
∴ 线段 AB 为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
典例精析
例1
如图,已知线段a,b,求作线段AB=2a-b.不写步骤,保留作图痕迹.
解:如图,线段AB即为所求作.
新知探究
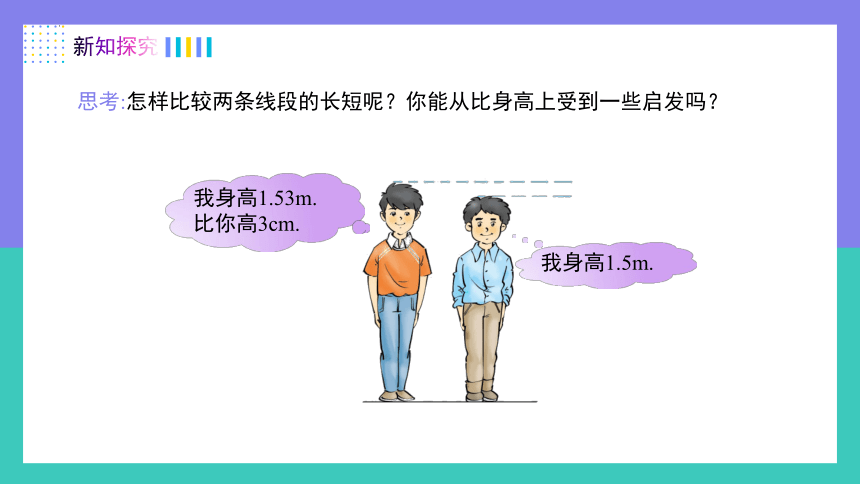
思考:怎样比较两条线段的长短呢?你能从比身高上受到一些启发吗?
我身高1.5m.
我身高1.53m.
比你高3cm.
新知探究
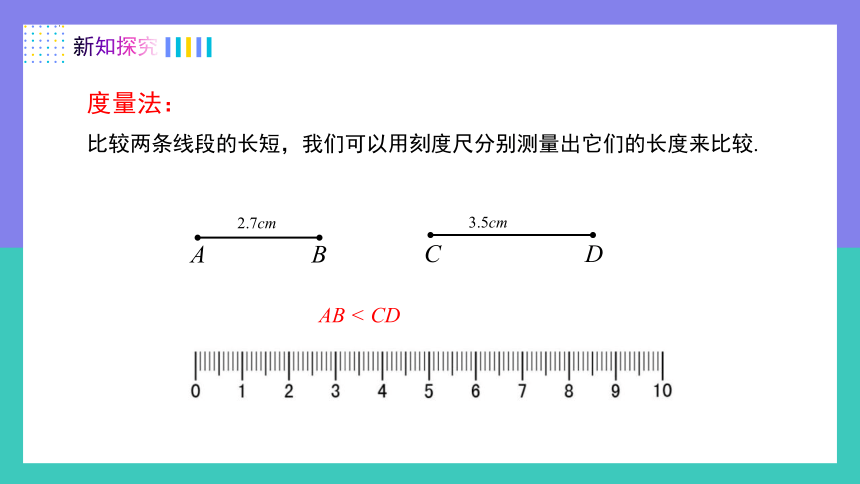
比较两条线段的长短,我们可以用刻度尺分别测量出它们的长度来比较.
C D
A B
2.7cm
3.5cm
AB < CD
度量法:
新知探究
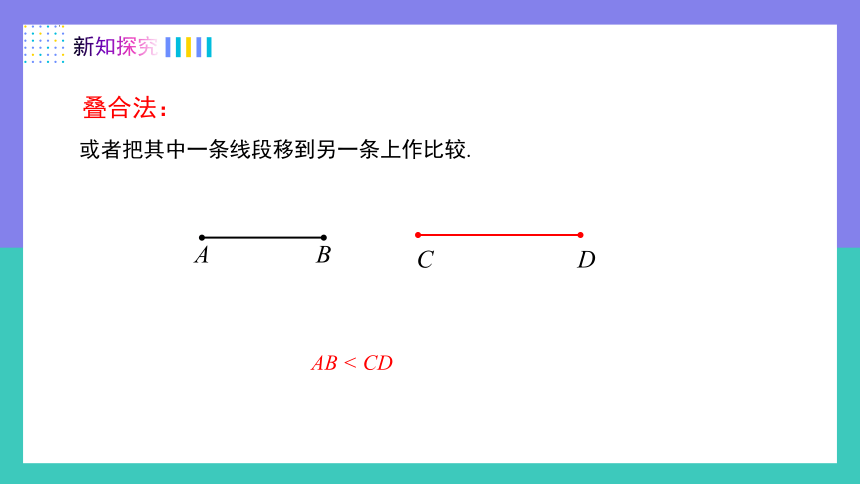
或者把其中一条线段移到另一条上作比较.
C D
A B
AB < CD
叠合法:
新知探究
C
D
1. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.
(A)
B
<
C
D
A
B
B
(A)
2. 若点 A 与点 C 重合,点 B 与
点 D ,那么 AB = CD.
3. 若点 A 与点 C 重合,点 B 落
在 CD 的延长线上,
那么 AB CD.
重合
>
B
A
B
A
C
D
(A)
(B)
新知探究
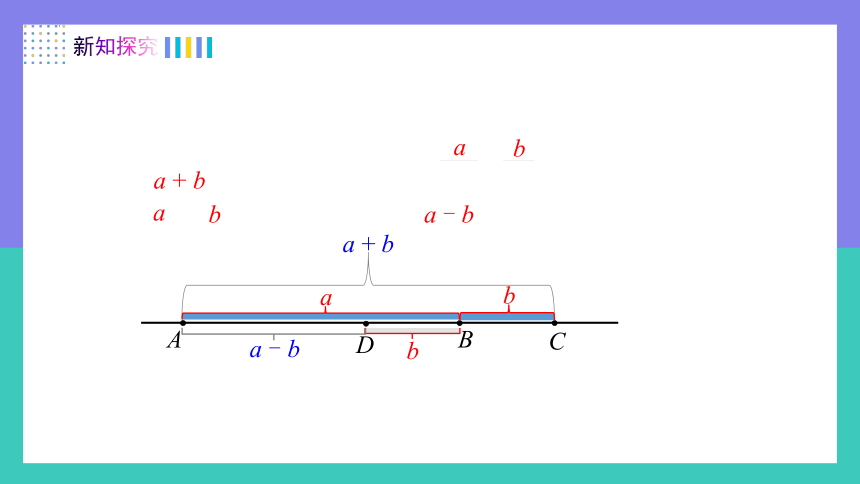
在直线上画出线段 AB = a,再在 AB 的延长线上画线段 BC = b,线段 AC 就是 与 的和,记作 AC = . 如果在 AB 上画线段 BD = b,那么线段 AD 就是 与 的差,记作 AD = .
A
B
C
D
a + b
a - b
a
b
b
a
b
a + b
a
b
a - b
1. 如图,点 B,C 在线段 AD 上,则 AB + BC =____, AD-CD =___,BC =___ -___ = ___ - ___.
新知探究
A
B
C
D
AC
AC
AC
AB
BD
CD
2. 如图,已知线段 a,b,画一条线段 AB,使 AB = 2a-b.
a
b
A
B
2a-b
2a
b
新知探究
条件 图形 作法 结论
用圆规在射线AE上截取线段AB=a,再在射线BE上截取线段BC=b
线段AC是线段a、b的和,即AC=a+b
用圆规在射线AE上截取线段AB=a,再在线段AB上截取线段BD=b
线段AD是线段a、b的差,即AD=a-b
典例精析
例2
估计下列图中线段AB与线段AC的大小关系,再用刻度尺或用圆规来
检验你的估计.
典例精析
例3
如图,填空:
(1)AD=AB+______=AC+_______=______+BC+______;
(2)AB=AD-______=AC-______=______-BC-______;
(3)AC+BD-AD=______.
BD
CD
AB
CD
BD
BC
AD
CD
BC
新知探究
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点. 类似地,还有线段的三等分点、四等分点等.
线段的三等分点
线段的四等分点
......
学习笔记
新知探究
A
a
a
M
B
M 是线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = BM = AB
(或 AB = 2AM = 2BM).
反之也成立:因为 AM = BM = AB
(或 AB = 2AM = 2BM),
所以 M 是线段 AB 的中点.
新知探究
点 M,N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
类似地,还有线段的四等分点,
如图②所示,
AB=BC=CD=DE=AE 或 AE=4AB=4BC=4CD=4DE.
典例精析
例4
如图,点 D 是线段 AB 的中点,点 C 是线段 AD 的中点,若 CD=1,
则AB= .
解:因为点 C 是线段 AD 的中点,
所以 AD=2CD =2.
因为点 D 是线段 AB 的中点,
所以 AB=2AD=4.
4
A
C
D
B
典例精析
例5
如图,点C是线段AB上的点,点D是线段BC的中点.
(1)若AB=10,AC=6,求CD的长;
解:(1)∵AB=10,AC=6,
∴BC=AB-AC=10-6=4.
∵点D是线段BC的中点,
∴CD= BC=2;
CD
BC
AB
AC
—
中 点
典例精析
(2)若AC=30,BD=10,求AB的长.
解:∵点D是线段BC的中点,
∴BC=2BD=2×10=20.
∵AB=AC+BC,
∴AB=30+20=50.
AB
BD
AC
BC
+
中 点
例5
如图,点C是线段AB上的点,点D是线段BC的中点.
典例精析
例6
如图,B、C 是线段 AD 上两点,且 AB : BC : CD = 3 : 2 : 5,E、F 分别是 AB、CD 的中点,且 EF = 24,求线段 AB、BC、CD 的长.
F
E
C
B
D
A
解:设 AB = 3x,BC = 2x,CD = 5x.
因为 E、F 分别是 AB、CD 的中点,
所以
所以 EF = BE + BC + CF =
因为 EF = 24,所以 6x = 24,解得 x = 4.
所以 AB = 3x = 12,BC = 2x = 8,CD = 5x = 20.
典例精析
例7
若线段AB=6,点C在直线AB上,BC=4,D是AC的中点,求A、
D两点间的距离.
解:分情况讨论:
(1)当点C在线段AB上时,如图:
所以AC=AB-BC=6-4=2,
因为D是AC的中点,
所以AD=1;
典例精析
例7
(2)当点C在线段AB的延长线上时,如图:
解:(2)
所以AC=AB+BC=6+4=10,
因为D是AC的中点,
所以AD=5.
综上所述,AD=1或5
学习笔记
典例精析
求线段的长度时,若题目中涉及线段长度的比例或倍分关系,通常可以设未知数,运用方程思想求解.
无图求线段的长时,应注意分类讨论,一般情况有:
点在线段上;
点在该线段的延长线上.
新知探究
思考:如图,小狗从 A 地到 B 地吃骨头有四条道路,你认为小狗会走哪条路?为什么
A
B
学习笔记
新知探究
1.线段的基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
2.两点间的距离:连接两点的线段的长度.
注:线段是一个图形,两点间的距离是指线段的长度,
是一个数值,而不是线段本身,因此不能说“A,B
两点间的距离是线段AB”,而应该说“A,B两点间
的距离是线段AB的长度”.
典例精析
例8
如图,A,B是公路(直线l)两旁的两个村庄.若两个村庄要在公路上合修一个汽车站,使它到A,B两个村庄的距离之和最小,试在直线l上标出汽车站的位置,并说明作图依据.
解:如图,连接AB交直线l于点P,则点P即为汽车站的位置.
依据:两点之间,线段最短.
l
B
A
·
·
·
典例精析
例9
公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?
两点之间,线段最短.
曲折迂回的桥增加了
游人在桥上行走的路程,
便于游人欣赏风光.
线段长短的比较与运算
比较
度量法、叠合法
基本事实
两点之间,线段最短
线段和差
中点、三等分点...
两点间的距离
方程思想、分类思想
随堂演练
1.如图,用圆规比较两条线段AB和A′B′的长短,结论正确的是( )
A.A′B′>AB
B.A′B′=AB
C.A′B′D.没有刻度尺,无法确定
C
随堂演练
2.点B在线段AC上,下列关系式:①AB= AC;②AB=BC;
③AC=2BC;④AB+BC=AC.其中能表示点B是线段AC的中点
的有( )
A.1个 B.2个 C.3个 D.4个
C
3. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
C
随堂演练
4.为比较线段AB、CD的长短,小明将点A与点C重合,使两条线段在一条直线上,点B在CD的延长线上,则( )
A.ABCD
C.AB=CD D.以上都有可能
B
5.如图,C,D是线段AB上两点.若AC=3,点C是线段AD的中点,AB=10,则B,D两点之间的距离是____.
4
随堂演练
6.下列四个现象中,可用“两点之间,线段最短”来解释的现象有( )
①用两个钉子就可以把木条固定在墙上;
②植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能地沿着直线架设;
④把弯曲的公路改直,就能缩短路程.
A.①② B.①③ C.②④ D.③④
D
随堂演练
7. 已知点M,N,P在同一条直线上,MN=3cm,NP=1cm.求线段MP的长.
解:如图(1),当点P在MN的延长线上时,
因为MP=MN+NP,所以MP=3+1=4(cm).
答:当点P在MN的延长线上时,线段MP的长为4cm;当点P在线段MN上时,线段MP的长为2cm.
N
M
P
(1)
3cm
1cm
N
M
P
(2)
3cm
1cm
如图(2),当点P在线段MN上时,
因为MP=MN-NP,所以MP=3-1=2(cm).
随堂演练
8.若C在线段AB的延长线上,且满足AC-CB=b cm,点M、N分别是AC、BC的中点,请猜想MN的长,并画出图形,说明理由.
6.2.2
线段的比较与运算
第6章 几何图形初步
情境引入
很多时候,眼见未必为实,准确比较线段的长短还需要更加严谨的办法.
观察下列图形,你能比较出上下两条线段 的长短吗?正方形的边长和圆的直径谁更长?
新知探究
在没有刻度尺的条件下,电工师傅若想从较长的电线上截下一段,使截下的电线等于另一根短电线的长,你有什么好办法吗?
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
思考:
新知探究
新知探究
尺规作图:画一条线段等于已知线段
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
∴ 线段 AB 为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
典例精析
例1
如图,已知线段a,b,求作线段AB=2a-b.不写步骤,保留作图痕迹.
解:如图,线段AB即为所求作.
新知探究
思考:怎样比较两条线段的长短呢?你能从比身高上受到一些启发吗?
我身高1.5m.
我身高1.53m.
比你高3cm.
新知探究
比较两条线段的长短,我们可以用刻度尺分别测量出它们的长度来比较.
C D
A B
2.7cm
3.5cm
AB < CD
度量法:
新知探究
或者把其中一条线段移到另一条上作比较.
C D
A B
AB < CD
叠合法:
新知探究
C
D
1. 若点 A 与点 C 重合,点 B 落
在C,D之间,那么 AB CD.
(A)
B
<
C
D
A
B
B
(A)
2. 若点 A 与点 C 重合,点 B 与
点 D ,那么 AB = CD.
3. 若点 A 与点 C 重合,点 B 落
在 CD 的延长线上,
那么 AB CD.
重合
>
B
A
B
A
C
D
(A)
(B)
新知探究
在直线上画出线段 AB = a,再在 AB 的延长线上画线段 BC = b,线段 AC 就是 与 的和,记作 AC = . 如果在 AB 上画线段 BD = b,那么线段 AD 就是 与 的差,记作 AD = .
A
B
C
D
a + b
a - b
a
b
b
a
b
a + b
a
b
a - b
1. 如图,点 B,C 在线段 AD 上,则 AB + BC =____, AD-CD =___,BC =___ -___ = ___ - ___.
新知探究
A
B
C
D
AC
AC
AC
AB
BD
CD
2. 如图,已知线段 a,b,画一条线段 AB,使 AB = 2a-b.
a
b
A
B
2a-b
2a
b
新知探究
条件 图形 作法 结论
用圆规在射线AE上截取线段AB=a,再在射线BE上截取线段BC=b
线段AC是线段a、b的和,即AC=a+b
用圆规在射线AE上截取线段AB=a,再在线段AB上截取线段BD=b
线段AD是线段a、b的差,即AD=a-b
典例精析
例2
估计下列图中线段AB与线段AC的大小关系,再用刻度尺或用圆规来
检验你的估计.
典例精析
例3
如图,填空:
(1)AD=AB+______=AC+_______=______+BC+______;
(2)AB=AD-______=AC-______=______-BC-______;
(3)AC+BD-AD=______.
BD
CD
AB
CD
BD
BC
AD
CD
BC
新知探究
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点. 类似地,还有线段的三等分点、四等分点等.
线段的三等分点
线段的四等分点
......
学习笔记
新知探究
A
a
a
M
B
M 是线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = BM = AB
(或 AB = 2AM = 2BM).
反之也成立:因为 AM = BM = AB
(或 AB = 2AM = 2BM),
所以 M 是线段 AB 的中点.
新知探究
点 M,N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
类似地,还有线段的四等分点,
如图②所示,
AB=BC=CD=DE=AE 或 AE=4AB=4BC=4CD=4DE.
典例精析
例4
如图,点 D 是线段 AB 的中点,点 C 是线段 AD 的中点,若 CD=1,
则AB= .
解:因为点 C 是线段 AD 的中点,
所以 AD=2CD =2.
因为点 D 是线段 AB 的中点,
所以 AB=2AD=4.
4
A
C
D
B
典例精析
例5
如图,点C是线段AB上的点,点D是线段BC的中点.
(1)若AB=10,AC=6,求CD的长;
解:(1)∵AB=10,AC=6,
∴BC=AB-AC=10-6=4.
∵点D是线段BC的中点,
∴CD= BC=2;
CD
BC
AB
AC
—
中 点
典例精析
(2)若AC=30,BD=10,求AB的长.
解:∵点D是线段BC的中点,
∴BC=2BD=2×10=20.
∵AB=AC+BC,
∴AB=30+20=50.
AB
BD
AC
BC
+
中 点
例5
如图,点C是线段AB上的点,点D是线段BC的中点.
典例精析
例6
如图,B、C 是线段 AD 上两点,且 AB : BC : CD = 3 : 2 : 5,E、F 分别是 AB、CD 的中点,且 EF = 24,求线段 AB、BC、CD 的长.
F
E
C
B
D
A
解:设 AB = 3x,BC = 2x,CD = 5x.
因为 E、F 分别是 AB、CD 的中点,
所以
所以 EF = BE + BC + CF =
因为 EF = 24,所以 6x = 24,解得 x = 4.
所以 AB = 3x = 12,BC = 2x = 8,CD = 5x = 20.
典例精析
例7
若线段AB=6,点C在直线AB上,BC=4,D是AC的中点,求A、
D两点间的距离.
解:分情况讨论:
(1)当点C在线段AB上时,如图:
所以AC=AB-BC=6-4=2,
因为D是AC的中点,
所以AD=1;
典例精析
例7
(2)当点C在线段AB的延长线上时,如图:
解:(2)
所以AC=AB+BC=6+4=10,
因为D是AC的中点,
所以AD=5.
综上所述,AD=1或5
学习笔记
典例精析
求线段的长度时,若题目中涉及线段长度的比例或倍分关系,通常可以设未知数,运用方程思想求解.
无图求线段的长时,应注意分类讨论,一般情况有:
点在线段上;
点在该线段的延长线上.
新知探究
思考:如图,小狗从 A 地到 B 地吃骨头有四条道路,你认为小狗会走哪条路?为什么
A
B
学习笔记
新知探究
1.线段的基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
2.两点间的距离:连接两点的线段的长度.
注:线段是一个图形,两点间的距离是指线段的长度,
是一个数值,而不是线段本身,因此不能说“A,B
两点间的距离是线段AB”,而应该说“A,B两点间
的距离是线段AB的长度”.
典例精析
例8
如图,A,B是公路(直线l)两旁的两个村庄.若两个村庄要在公路上合修一个汽车站,使它到A,B两个村庄的距离之和最小,试在直线l上标出汽车站的位置,并说明作图依据.
解:如图,连接AB交直线l于点P,则点P即为汽车站的位置.
依据:两点之间,线段最短.
l
B
A
·
·
·
典例精析
例9
公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?
两点之间,线段最短.
曲折迂回的桥增加了
游人在桥上行走的路程,
便于游人欣赏风光.
线段长短的比较与运算
比较
度量法、叠合法
基本事实
两点之间,线段最短
线段和差
中点、三等分点...
两点间的距离
方程思想、分类思想
随堂演练
1.如图,用圆规比较两条线段AB和A′B′的长短,结论正确的是( )
A.A′B′>AB
B.A′B′=AB
C.A′B′
C
随堂演练
2.点B在线段AC上,下列关系式:①AB= AC;②AB=BC;
③AC=2BC;④AB+BC=AC.其中能表示点B是线段AC的中点
的有( )
A.1个 B.2个 C.3个 D.4个
C
3. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
C
随堂演练
4.为比较线段AB、CD的长短,小明将点A与点C重合,使两条线段在一条直线上,点B在CD的延长线上,则( )
A.AB
C.AB=CD D.以上都有可能
B
5.如图,C,D是线段AB上两点.若AC=3,点C是线段AD的中点,AB=10,则B,D两点之间的距离是____.
4
随堂演练
6.下列四个现象中,可用“两点之间,线段最短”来解释的现象有( )
①用两个钉子就可以把木条固定在墙上;
②植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能地沿着直线架设;
④把弯曲的公路改直,就能缩短路程.
A.①② B.①③ C.②④ D.③④
D
随堂演练
7. 已知点M,N,P在同一条直线上,MN=3cm,NP=1cm.求线段MP的长.
解:如图(1),当点P在MN的延长线上时,
因为MP=MN+NP,所以MP=3+1=4(cm).
答:当点P在MN的延长线上时,线段MP的长为4cm;当点P在线段MN上时,线段MP的长为2cm.
N
M
P
(1)
3cm
1cm
N
M
P
(2)
3cm
1cm
如图(2),当点P在线段MN上时,
因为MP=MN-NP,所以MP=3-1=2(cm).
随堂演练
8.若C在线段AB的延长线上,且满足AC-CB=b cm,点M、N分别是AC、BC的中点,请猜想MN的长,并画出图形,说明理由.
同课章节目录
