22.3实际问题与二次函数(预习衔接.含解析)-2025-2026学年九年级上册数学人教版
文档属性
| 名称 | 22.3实际问题与二次函数(预习衔接.含解析)-2025-2026学年九年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 17:46:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新课预习衔接 实际问题与二次函数
一.选择题(共5小题)
1.(2024 中山市校级期末)一个球从地面竖直向上弹起时的速度为20米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=20t﹣5t2,那么球弹起后又回到地面所花的时间t(秒)是( )
A.2 B.4 C.5 D.20
2.(2024 鞍山模拟)如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s D.小球飞出1s时的飞行高度为10m
3.(2024 榆林期末)二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
4.(2024 河北模拟)已知二次函数y=(x﹣h)2+1(h为常数)在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
5.(2024 邓州市二模)如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线解析式为y,正常水位时水面宽AB为36m,当水位上升5m时水面宽CD为( )
A.10m B.12m C.24m D.48m
二.填空题(共5小题)
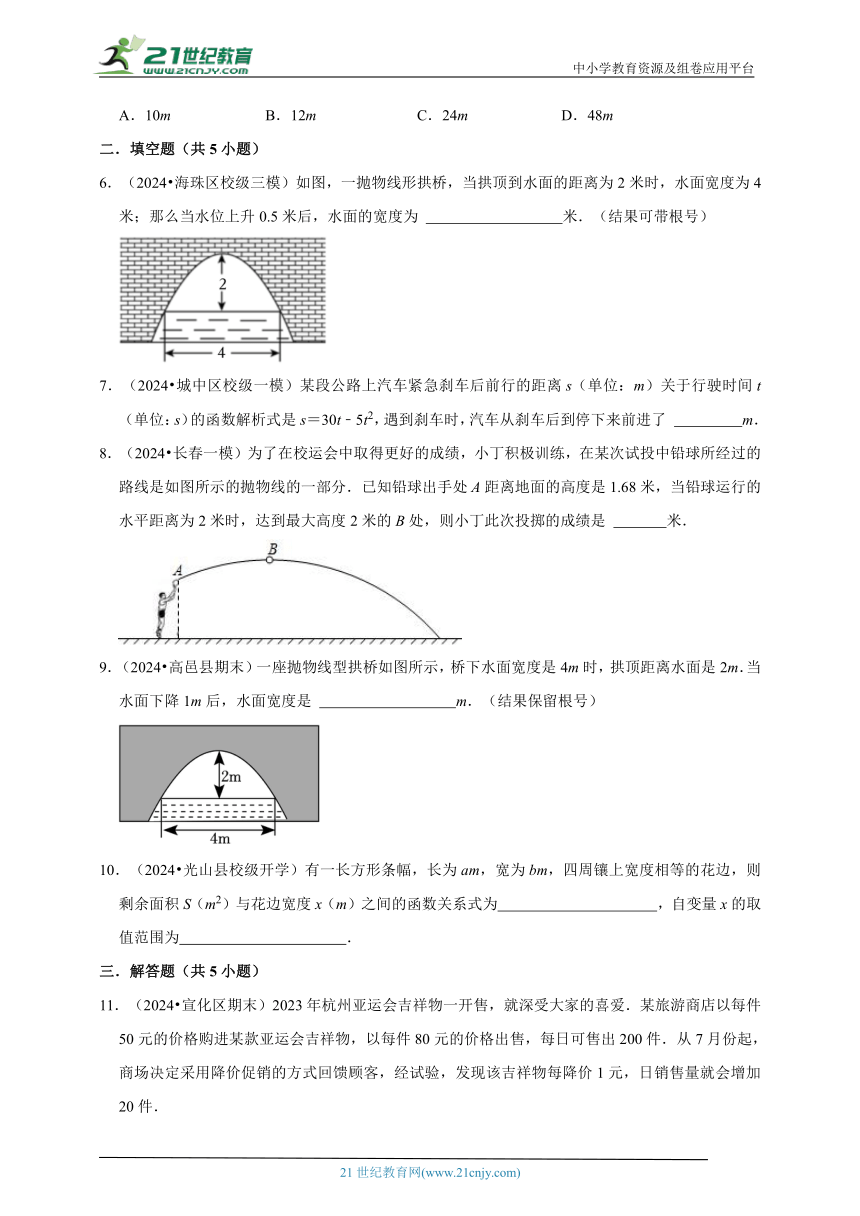
6.(2024 海珠区校级三模)如图,一抛物线形拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位上升0.5米后,水面的宽度为 米.(结果可带根号)
7.(2024 城中区校级一模)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 m.
8.(2024 长春一模)为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 米.
9.(2024 高邑县期末)一座抛物线型拱桥如图所示,桥下水面宽度是4m时,拱顶距离水面是2m.当水面下降1m后,水面宽度是 m.(结果保留根号)
10.(2024 光山县校级开学)有一长方形条幅,长为am,宽为bm,四周镶上宽度相等的花边,则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为 ,自变量x的取值范围为 .
三.解答题(共5小题)
11.(2024 宣化区期末)2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某旅游商店以每件50元的价格购进某款亚运会吉祥物,以每件80元的价格出售,每日可售出200件.从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,日销售量就会增加20件.
(1)设定价为x元,日销售量为y件.试用含x的式子表示y,y= ;
(2)当该吉祥物售价为多少元时,日销售利润达7500元?
(3)请你测算一下,该商场如何定价,可使日销售利润最多?
12.(2024 陇西县期末)中国茶文化是中国传统文化的重要组成部分之一,代表了中国文化的精髓和卓越,具有丰富的文化内涵和深远的历史意义.某茶庄经销一种绿茶,每千克成本为50元,经市场调查发现:在一段时间内,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为W=﹣2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x之间的函数关系式;
(2)当绿茶的销售单价是多少时,该茶庄这种绿茶在这段时间内的销售利润最大?最大利润是多少?
13.(2024 凉州区三模)如图1所示是一座古桥,桥拱截面为抛物线,如图2,AO,BC是桥墩,桥的跨径AB为20m,此时水位在OC处,桥拱最高点P离水面6m,在水面以上的桥墩AO,BC都为2m.以OC所在的直线为x轴、AO所在的直线为y轴建立平面直角坐标系,其中x(m)是桥拱截面上一点距桥墩AO的水平距离,y(m)是桥拱截面上一点距水面OC的距离.
(1)求此桥拱截面所在抛物线的表达式;
(2)有一艘游船,其左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在河中航行.当水位上涨2m时,水面到棚顶的高度为3m,遮阳棚宽12m,问此船能否通过桥洞?请说明理由.
14.(2024 右玉县四模)某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) 1月 2月 3月 4月 5月 6月
销售量(p) 3.9万台 4.0万台 4.1万台 4.2万台 4.3万台 4.4万台
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
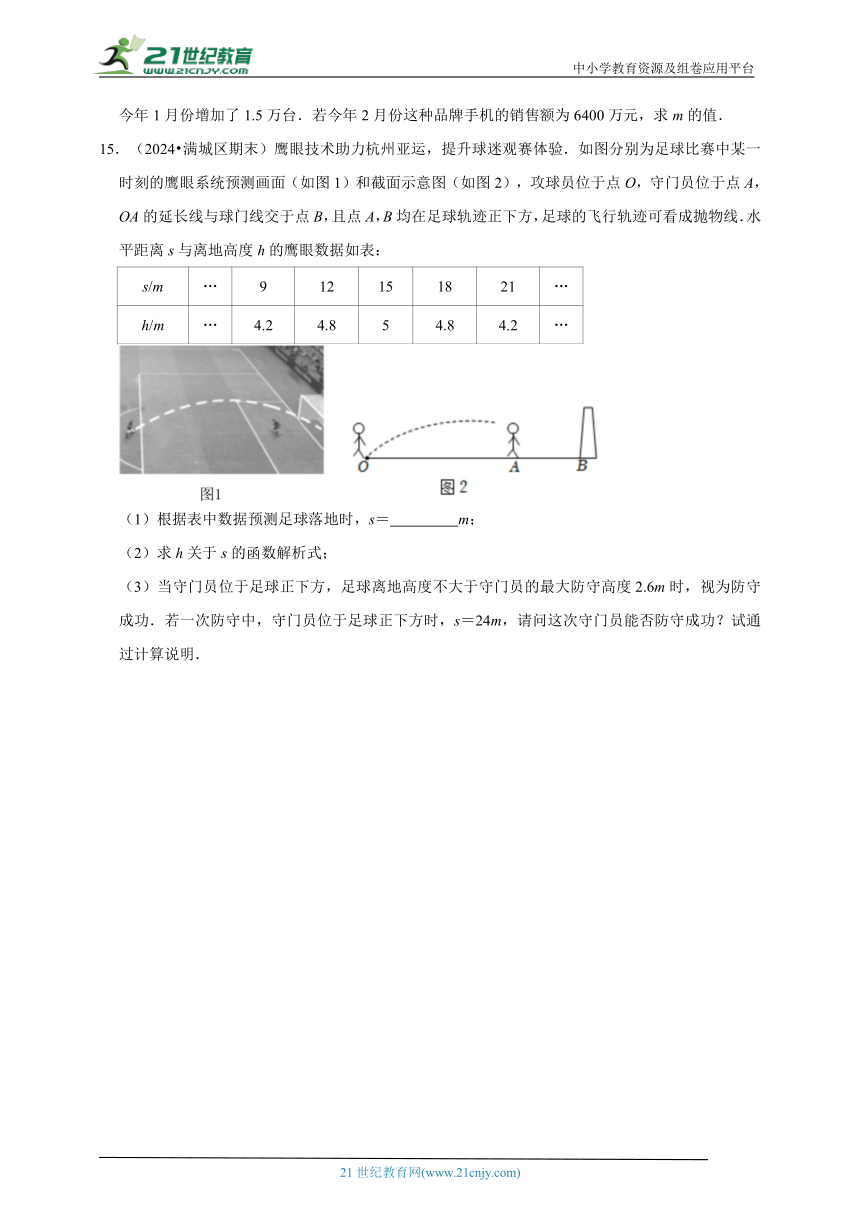
15.(2024 满城区期末)鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点O,守门员位于点A,OA的延长线与球门线交于点B,且点A,B均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离s与离地高度h的鹰眼数据如表:
s/m … 9 12 15 18 21 …
h/m … 4.2 4.8 5 4.8 4.2 …
(1)根据表中数据预测足球落地时,s= m;
(2)求h关于s的函数解析式;
(3)当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度2.6m时,视为防守成功.若一次防守中,守门员位于足球正下方时,s=24m,请问这次守门员能否防守成功?试通过计算说明.
新课预习衔接 实际问题与二次函数
参考答案与试题解析
一.选择题(共5小题)
1.(2024 中山市校级期末)一个球从地面竖直向上弹起时的速度为20米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=20t﹣5t2,那么球弹起后又回到地面所花的时间t(秒)是( )
A.2 B.4 C.5 D.20
【考点】二次函数的应用.
【专题】二次函数的应用;推理能力.
【答案】B
【分析】令h=0,求出t值即可.
【解答】解:令h=0,得:20t﹣5t2=0,
解得:t=0或t=4,
∴那么球弹起后又回到地面所花的时间是4秒;
故选:B.
【点评】本题主要考查二次函数的应用,熟练掌握二次函数的图象和性质是解题的关键.
2.(2024 鞍山模拟)如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m
B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s
D.小球飞出1s时的飞行高度为10m
【考点】二次函数的应用.
【专题】二次函数的应用.
【答案】C
【分析】直接利用h=15以及结合配方法求出二次函数最值分别分析得出答案.
【解答】解:A、当h=15时,15=20t﹣5t2,
解得:t1=1,t2=3,
故小球的飞行高度能达到15m,故此选项错误;
B、h=20t﹣5t2=﹣5(t﹣2)2+20,
故t=2时,小球的飞行高度最大为:20m,故此选项错误;
C、∵h=0时,0=20t﹣5t2,
解得:t1=0,t2=4,
∴小球从飞出到落地要用时4s,故此选项正确;
D、当t=1时,h=15,
故小球飞出1s时的飞行高度为15m,故此选项错误;
故选:C.
【点评】此题主要考查了二次函数的应用,正确解方程是解题关键.
3.(2024 榆林期末)二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
【考点】二次函数的最值.
【专题】二次函数图象及其性质;推理能力.
【答案】A
【分析】由二次函数解析式可得抛物线开口方向及对称轴,从而可得在﹣3≤x≤2的范围内函数取最小值时x的值,进而求解.
【解答】解:∵y=﹣x2﹣2x+c2﹣2c=﹣(x+1)2+c2﹣2c+1,
∴抛物线开口向下,对称轴为直线x=﹣1,
∵2﹣(﹣1)>﹣1﹣(﹣3),
∴在﹣3≤x≤2的范围内,x=2时,y=﹣4﹣4+c2﹣2c=c2﹣2c﹣8=(c﹣1)2﹣9为函数最小值,
∴(c﹣1)2﹣9=﹣5,
解得c=3或c=﹣1,
故选:A.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数图象与系数的关系,掌握二次函数与不等式的关系.
4.(2024 河北模拟)已知二次函数y=(x﹣h)2+1(h为常数)在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
【考点】二次函数的最值.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】当h<1≤x≤3时,二次函数在1≤x≤3上单调递增,进而得出x=1时,y取得最小值5,进而求出h的值;当1≤x≤3<h,二次函数在1≤x≤3上单调递减,进而得出x=3时,y取得最小值5,进而求出h的值.
【解答】解:h的值不可能在1到3之间,
当h<1≤x≤3时,
当x=1时,y取得最小值5,
(1﹣h)2+1=5,
h=﹣1或h=3(不合题意,舍去),
当1≤x≤3<h,
当x=3时,y取得最小值5,
(3﹣h)2+1=5,
h=5或h=1(不合题意,舍去),
故选:B.
【点评】本题主要是函数的单调性以及最值问题,正确理解二次函数的单调性是解题关键.
5.(2024 邓州市二模)如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线解析式为y,正常水位时水面宽AB为36m,当水位上升5m时水面宽CD为( )
A.10m B.12m C.24m D.48m
【考点】二次函数的应用.
【专题】二次函数图象及其性质;数据分析观念.
【答案】C
【分析】根据正常水位时水面宽AB,求出当x=18时y=﹣9,再根据水位上升5米时y=﹣4,代入解析式求出x即可.
【解答】解:∵AB=36米,
∴当x=18时,y182=﹣9,
当水位上升5米时,y=﹣4,
把y=﹣4代入抛物线表达式得:﹣4x2,
解得x=±12,
此时水面宽CD=24(m),
故选:C.
【点评】本题考查二次函数的应用,关键是通过建立适当坐标系求出抛物线解析式.
二.填空题(共5小题)
6.(2024 海珠区校级三模)如图,一抛物线形拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位上升0.5米后,水面的宽度为 2 米.(结果可带根号)
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】2.
【分析】根据题意设抛物线解析式,求出解析式确定出水面的宽度即可.
【解答】解:建立如图所示的直角坐标系,
设抛物线解析式为y=ax2+c,
把(2,0)和(0,2)代入得,
,
解得,
∴抛物线解析式为yx2+2,
把y=0.5代入得:x=±,
则水面的宽度是2米.
故答案为:2.
【点评】此题考查了二次函数的应用,熟练掌握待定系数法是解本题的关键.
7.(2024 城中区校级一模)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 45 m.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】45.
【分析】根据二次函数的解析式找出其顶点式,再利用二次函数的性质求出s的最大值即可得出结论.【解答】【点评】
【解答】解:∵s=﹣5t2+30t=﹣5(t﹣3)2+45,
∴汽车刹车后到停下来前进了45m,
故答案为:45.
【点评】本题考查了二次函数的应用,利用配方法,求出二次函数的顶点式是解题的关键.
8.(2024 长春一模)为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 7 米.
【考点】二次函数的应用.
【专题】数形结合;待定系数法;一元二次方程及应用;二次函数图象及其性质;二次函数的应用;几何直观;运算能力;应用意识.
【答案】见试题解答内容
【分析】建立坐标系,设抛物线的解析式为y=a(x﹣2)2+2,由待定系数法求得抛物线的解析式,令y=0,得关于x的一元二次方程,求得方程的解并根据问题的实际意义作出取舍即可.
【解答】解:建立坐标系,如图所示:
由题意得:A(0,1.68),B(2,2),点B为抛物线的顶点,
设抛物线的解析式为y=a(x﹣2)2+2,
把A(0,1.68)代入得:
4a+2=1.68,
解得a=﹣0.08,
∴y=﹣0.08(x﹣2)2+2,
令y=0,得﹣0.08(x﹣2)2+2=0,
解得x1=7,x2=﹣3(舍),
∴小丁此次投掷的成绩是7米.
故答案为:7.
【点评】本题考查了二次函数在实际问题中的应用,正确建立平面直角坐标系、熟练掌握待定系数法及二次函数与一元二次方程的关系是解题的关键.
9.(2024 高邑县期末)一座抛物线型拱桥如图所示,桥下水面宽度是4m时,拱顶距离水面是2m.当水面下降1m后,水面宽度是 2 m.(结果保留根号)
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】2.
【分析】根据题意,建立合适的平面直角坐标系,然后求出抛物线的解析式,再将y=﹣3代入函数解析式,求出x的值,然后即可求得水面下降1m后,水面宽度.
【解答】解:建立平面直角坐标系,如图所示,
设该抛物线的解析式为y=ax2,
由题意可知:点(2,﹣2)在该函数图象上,
∴﹣2=a×22,
解得a,
∴该抛物线的解析式为yx2,
当y=﹣3时,﹣3x2,
解得x1,x2,
∴当水面下降1m后,水面宽度是:()2(m),
故答案为:2.
【点评】本题考查二次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式.
10.(2024 光山县校级开学)有一长方形条幅,长为am,宽为bm,四周镶上宽度相等的花边,则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为 s=(a﹣2x)(b﹣2x) ,自变量x的取值范围为 0<x .
【考点】根据实际问题列二次函数关系式.
【答案】见试题解答内容
【分析】因为四周镶上宽度相等的花边,所以剩余长方形的长为(a﹣2x),宽为(b﹣2x),利用长方形的面积公式:长×宽,可表示出函数关系式;2x应该小于宽b,可求得x的上限,下限为x>0,所以可求出自变量x的取值范围.
【解答】解:剩余长方形的长为(a﹣2x),宽为(b﹣2x),
则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为:s=(a﹣2x)(b﹣2x).
∵x>0,2x<b
∴自变量x的取值范围为0<x.
故答案为:s=(a﹣2x)(b﹣2x);0<x.
【点评】主要考查了二次函数的实际运用.用含x的代数式表示出长和宽,再根据长方形的面积公式即可表示出二次函数的解析式.
三.解答题(共5小题)
11.(2024 宣化区期末)2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某旅游商店以每件50元的价格购进某款亚运会吉祥物,以每件80元的价格出售,每日可售出200件.从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,日销售量就会增加20件.
(1)设定价为x元,日销售量为y件.试用含x的式子表示y,y= ﹣20x+1800 ;
(2)当该吉祥物售价为多少元时,日销售利润达7500元?
(3)请你测算一下,该商场如何定价,可使日销售利润最多?
【考点】二次函数的应用;一元二次方程的应用.
【专题】二次函数的应用;运算能力.
【答案】见试题解答内容
【分析】(1)销售量=降价前每日销售量+降价所增加的销售量,据此即可求解;
(2)每件所获利润×日销售量=7500元,据此即可求解;
(3)设日销售利润为W元,日销售利润=每件所获利润×日销售量,据此即可求解.
【解答】解:(1)y=200+20(80﹣x)
=﹣20x+1800,
故答案为:﹣20x+1800;
(2)由题意得:
(x﹣50)(﹣20x+1800)=7500,
整理得:x2﹣140x+4875=0,
解得:x1=65,x2=75,
∵降价促销,
∴x2=75舍去,
∴x=65,
答:该吉祥物售价为65元时,日销售利润达7500元.
(3)设日销售利润为W元,由题意得:
W=(x﹣50)(﹣20x+1800)
=﹣20(x﹣70)2+8000,
∵﹣20<0,
∴当x=70时,W最大=8000(元);
答:每件售价为70元时,可使日销售利润最多.
【点评】本题考查一次函数在销售问题的应用,一元二次方程在销售问题中应用,二次函数在销售问题中的应用,找出等量关系式是解题的关键.
12.(2024 陇西县期末)中国茶文化是中国传统文化的重要组成部分之一,代表了中国文化的精髓和卓越,具有丰富的文化内涵和深远的历史意义.某茶庄经销一种绿茶,每千克成本为50元,经市场调查发现:在一段时间内,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为W=﹣2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x之间的函数关系式;
(2)当绿茶的销售单价是多少时,该茶庄这种绿茶在这段时间内的销售利润最大?最大利润是多少?
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)y=﹣2x2+340x﹣12000;
(2)当绿茶的销售单价是85元/千克时,该茶庄这种绿茶在这段时间内的销售利润最大,最大利润是2450元.
【分析】(1)根据销售利润=销量×(销售单价﹣每千克成本)可求出关系式;
(2)用配方法或公式法来求二次函数最大值的问题.
【解答】解:(1)y=(x﹣50) W=(x﹣50)(﹣2x+240)=﹣2x2+340x﹣12000,
∴y与x之间的函数关系式为:y=﹣2x2+340x﹣12000.
(2)y=﹣2x2+340x﹣12000=﹣2(x﹣85)2+2450,
∴当x=85时,y的值最大,最大为2450元.
即当绿茶的销售单价是85元/千克时,该茶庄这种绿茶在这段时间内的销售利润最大,最大利润是2450元.
【点评】本题主要考查了二次函数的应用,解决本题的关键要找出等量关系,列出二次函数解析式,用配方法或公式法来求二次函数最大值.
13.(2024 凉州区三模)如图1所示是一座古桥,桥拱截面为抛物线,如图2,AO,BC是桥墩,桥的跨径AB为20m,此时水位在OC处,桥拱最高点P离水面6m,在水面以上的桥墩AO,BC都为2m.以OC所在的直线为x轴、AO所在的直线为y轴建立平面直角坐标系,其中x(m)是桥拱截面上一点距桥墩AO的水平距离,y(m)是桥拱截面上一点距水面OC的距离.
(1)求此桥拱截面所在抛物线的表达式;
(2)有一艘游船,其左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在河中航行.当水位上涨2m时,水面到棚顶的高度为3m,遮阳棚宽12m,问此船能否通过桥洞?请说明理由.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)此桥拱截面所在抛物线的表达式为;
(2)此船不能通过桥洞.理由见解析.
【分析】(1)先求出点A,点B,点P的坐标,再把抛物线解析式设为顶点式进行求解即可;
(2)求出当y=5时x的值,然后计算出两个对应的x的值之间的差的绝对值即可得到答案.
【解答】解:(1)由题意知,A(0,2),P(10,6),B(20,2),
设抛物线解析式为y=a(x﹣10)2+6,
把A(0,2)代入解析式得,100a+6=2,
解得,
∴此桥拱截面所在抛物线的表达式为;
(2)此船不能通过,理由:
当y=2+3=5时,,
解得x=5或x=15,
∵15﹣5=10<12,
∴此船不能通过桥洞.
【点评】本题考查二次函数的应用,熟练掌握二次函数的图象与性质是解本题的关键【点睛】本题考查二次函数的应用,熟练掌握二次函数的图象与性质是解本题的关键.
14.(2024 右玉县四模)某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) 1月 2月 3月 4月 5月 6月
销售量(p) 3.9万台 4.0万台 4.1万台 4.2万台 4.3万台 4.4万台
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
【考点】二次函数的应用.
【答案】见试题解答内容
【分析】(1)直接利用待定系数法求一次函数解析式即可;
(2)利用销量×售价=销售金额,进而利用二次函数最值求法求出即可;
(3)分别表示出1,2月份的销量以及售价,进而利用今年2月份这种品牌手机的销售额为6400万元,得出等式求出即可.
【解答】解:(1)设p=kx+b,
把p=3.9,x=1;p=4.0,x=2分别代入p=kx+b中,
得:,
解得:,
∴p=0.1x+3.8;
(2)设该品牌手机在去年第x个月的销售金额为w万元,
w=(﹣50x+2600)(0.1x+3.8)
=﹣5x2+70x+9880
=﹣5(x﹣7)2+10125,
当x=7时,w最大=10125,
答:该品牌手机在去年七月份的销售金额最大,最大为10125万元;
(3)当x=12时,y=2000,p=5,
1月份的售价为:2000(1﹣m%)元,则2月份的售价为:0.8×2000(1﹣m%)元;
1月份的销量为:5×(1﹣1.5m%)万台,则2月份的销量为:[5×(1﹣1.5m%)+1.5]万台;
∴0.8×2000(1﹣m%)×[5×(1﹣1.5m%)+1.5]=6400,
解得:m1%(舍去),m2%,
∴m=20,
答:m的值为20.
【点评】此题主要考查了二次函数的应用以及待定系数法求一次函数解析式,根据题意表示出2月份的销量与售价是解题关键.
15.(2024 满城区期末)鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点O,守门员位于点A,OA的延长线与球门线交于点B,且点A,B均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离s与离地高度h的鹰眼数据如表:
s/m … 9 12 15 18 21 …
h/m … 4.2 4.8 5 4.8 4.2 …
(1)根据表中数据预测足球落地时,s= 30 m;
(2)求h关于s的函数解析式;
(3)当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度2.6m时,视为防守成功.若一次防守中,守门员位于足球正下方时,s=24m,请问这次守门员能否防守成功?试通过计算说明.
【考点】二次函数的应用.
【专题】二次函数图象及其性质;二次函数的应用;运算能力.
【答案】见试题解答内容
【分析】(1)根据抛物线的对称轴可直接得出结论;
(2)根据抛物线的对称性找到顶点,设出顶点式,再代入(12,4.8)可求出参数,由此可解答;
(3)根据s的值,求出h,再与最大防守高度2.6m比较即可.
【解答】解:(1)由表格可知,s=9时和s=21时,h相等,s=12时,s=18时,h相等,
抛物线关于s=15对称,
∵当s=0时,h=0,
∴s=30时,h=0,
故答案为:30.
(2)由(1)知,抛物线关于s=15对称,设h=a(s﹣15)2+5,
把(12,4.8)代入上述解析式,
∴a(12﹣15)2+5=4.8,解得a,
∴h(s﹣15)2+5,
即hs2s;
(3)不能防守成功,
理由如下:当s=24m时,hs2s24224=3.2(m),
∵3.2>2.6,
∴这次守门员不能防守成功.
【点评】本题考查二次函数的实际应用,理解题意,掌握抛物线的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 实际问题与二次函数
一.选择题(共5小题)
1.(2024 中山市校级期末)一个球从地面竖直向上弹起时的速度为20米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=20t﹣5t2,那么球弹起后又回到地面所花的时间t(秒)是( )
A.2 B.4 C.5 D.20
2.(2024 鞍山模拟)如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s D.小球飞出1s时的飞行高度为10m
3.(2024 榆林期末)二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
4.(2024 河北模拟)已知二次函数y=(x﹣h)2+1(h为常数)在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
5.(2024 邓州市二模)如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线解析式为y,正常水位时水面宽AB为36m,当水位上升5m时水面宽CD为( )
A.10m B.12m C.24m D.48m
二.填空题(共5小题)
6.(2024 海珠区校级三模)如图,一抛物线形拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位上升0.5米后,水面的宽度为 米.(结果可带根号)
7.(2024 城中区校级一模)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 m.
8.(2024 长春一模)为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 米.
9.(2024 高邑县期末)一座抛物线型拱桥如图所示,桥下水面宽度是4m时,拱顶距离水面是2m.当水面下降1m后,水面宽度是 m.(结果保留根号)
10.(2024 光山县校级开学)有一长方形条幅,长为am,宽为bm,四周镶上宽度相等的花边,则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为 ,自变量x的取值范围为 .
三.解答题(共5小题)
11.(2024 宣化区期末)2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某旅游商店以每件50元的价格购进某款亚运会吉祥物,以每件80元的价格出售,每日可售出200件.从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,日销售量就会增加20件.
(1)设定价为x元,日销售量为y件.试用含x的式子表示y,y= ;
(2)当该吉祥物售价为多少元时,日销售利润达7500元?
(3)请你测算一下,该商场如何定价,可使日销售利润最多?
12.(2024 陇西县期末)中国茶文化是中国传统文化的重要组成部分之一,代表了中国文化的精髓和卓越,具有丰富的文化内涵和深远的历史意义.某茶庄经销一种绿茶,每千克成本为50元,经市场调查发现:在一段时间内,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为W=﹣2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x之间的函数关系式;
(2)当绿茶的销售单价是多少时,该茶庄这种绿茶在这段时间内的销售利润最大?最大利润是多少?
13.(2024 凉州区三模)如图1所示是一座古桥,桥拱截面为抛物线,如图2,AO,BC是桥墩,桥的跨径AB为20m,此时水位在OC处,桥拱最高点P离水面6m,在水面以上的桥墩AO,BC都为2m.以OC所在的直线为x轴、AO所在的直线为y轴建立平面直角坐标系,其中x(m)是桥拱截面上一点距桥墩AO的水平距离,y(m)是桥拱截面上一点距水面OC的距离.
(1)求此桥拱截面所在抛物线的表达式;
(2)有一艘游船,其左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在河中航行.当水位上涨2m时,水面到棚顶的高度为3m,遮阳棚宽12m,问此船能否通过桥洞?请说明理由.
14.(2024 右玉县四模)某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) 1月 2月 3月 4月 5月 6月
销售量(p) 3.9万台 4.0万台 4.1万台 4.2万台 4.3万台 4.4万台
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
15.(2024 满城区期末)鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点O,守门员位于点A,OA的延长线与球门线交于点B,且点A,B均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离s与离地高度h的鹰眼数据如表:
s/m … 9 12 15 18 21 …
h/m … 4.2 4.8 5 4.8 4.2 …
(1)根据表中数据预测足球落地时,s= m;
(2)求h关于s的函数解析式;
(3)当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度2.6m时,视为防守成功.若一次防守中,守门员位于足球正下方时,s=24m,请问这次守门员能否防守成功?试通过计算说明.
新课预习衔接 实际问题与二次函数
参考答案与试题解析
一.选择题(共5小题)
1.(2024 中山市校级期末)一个球从地面竖直向上弹起时的速度为20米/秒,经过t(秒)时球距离地面的高度h(米)适用公式h=20t﹣5t2,那么球弹起后又回到地面所花的时间t(秒)是( )
A.2 B.4 C.5 D.20
【考点】二次函数的应用.
【专题】二次函数的应用;推理能力.
【答案】B
【分析】令h=0,求出t值即可.
【解答】解:令h=0,得:20t﹣5t2=0,
解得:t=0或t=4,
∴那么球弹起后又回到地面所花的时间是4秒;
故选:B.
【点评】本题主要考查二次函数的应用,熟练掌握二次函数的图象和性质是解题的关键.
2.(2024 鞍山模拟)如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m
B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s
D.小球飞出1s时的飞行高度为10m
【考点】二次函数的应用.
【专题】二次函数的应用.
【答案】C
【分析】直接利用h=15以及结合配方法求出二次函数最值分别分析得出答案.
【解答】解:A、当h=15时,15=20t﹣5t2,
解得:t1=1,t2=3,
故小球的飞行高度能达到15m,故此选项错误;
B、h=20t﹣5t2=﹣5(t﹣2)2+20,
故t=2时,小球的飞行高度最大为:20m,故此选项错误;
C、∵h=0时,0=20t﹣5t2,
解得:t1=0,t2=4,
∴小球从飞出到落地要用时4s,故此选项正确;
D、当t=1时,h=15,
故小球飞出1s时的飞行高度为15m,故此选项错误;
故选:C.
【点评】此题主要考查了二次函数的应用,正确解方程是解题关键.
3.(2024 榆林期末)二次函数y=﹣x2﹣2x+c2﹣2c在﹣3≤x≤2的范围内有最小值为﹣5,则c的值为( )
A.3或﹣1 B.﹣1 C.﹣3或1 D.3
【考点】二次函数的最值.
【专题】二次函数图象及其性质;推理能力.
【答案】A
【分析】由二次函数解析式可得抛物线开口方向及对称轴,从而可得在﹣3≤x≤2的范围内函数取最小值时x的值,进而求解.
【解答】解:∵y=﹣x2﹣2x+c2﹣2c=﹣(x+1)2+c2﹣2c+1,
∴抛物线开口向下,对称轴为直线x=﹣1,
∵2﹣(﹣1)>﹣1﹣(﹣3),
∴在﹣3≤x≤2的范围内,x=2时,y=﹣4﹣4+c2﹣2c=c2﹣2c﹣8=(c﹣1)2﹣9为函数最小值,
∴(c﹣1)2﹣9=﹣5,
解得c=3或c=﹣1,
故选:A.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数图象与系数的关系,掌握二次函数与不等式的关系.
4.(2024 河北模拟)已知二次函数y=(x﹣h)2+1(h为常数)在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或3
【考点】二次函数的最值.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】当h<1≤x≤3时,二次函数在1≤x≤3上单调递增,进而得出x=1时,y取得最小值5,进而求出h的值;当1≤x≤3<h,二次函数在1≤x≤3上单调递减,进而得出x=3时,y取得最小值5,进而求出h的值.
【解答】解:h的值不可能在1到3之间,
当h<1≤x≤3时,
当x=1时,y取得最小值5,
(1﹣h)2+1=5,
h=﹣1或h=3(不合题意,舍去),
当1≤x≤3<h,
当x=3时,y取得最小值5,
(3﹣h)2+1=5,
h=5或h=1(不合题意,舍去),
故选:B.
【点评】本题主要是函数的单调性以及最值问题,正确理解二次函数的单调性是解题关键.
5.(2024 邓州市二模)如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线解析式为y,正常水位时水面宽AB为36m,当水位上升5m时水面宽CD为( )
A.10m B.12m C.24m D.48m
【考点】二次函数的应用.
【专题】二次函数图象及其性质;数据分析观念.
【答案】C
【分析】根据正常水位时水面宽AB,求出当x=18时y=﹣9,再根据水位上升5米时y=﹣4,代入解析式求出x即可.
【解答】解:∵AB=36米,
∴当x=18时,y182=﹣9,
当水位上升5米时,y=﹣4,
把y=﹣4代入抛物线表达式得:﹣4x2,
解得x=±12,
此时水面宽CD=24(m),
故选:C.
【点评】本题考查二次函数的应用,关键是通过建立适当坐标系求出抛物线解析式.
二.填空题(共5小题)
6.(2024 海珠区校级三模)如图,一抛物线形拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位上升0.5米后,水面的宽度为 2 米.(结果可带根号)
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】2.
【分析】根据题意设抛物线解析式,求出解析式确定出水面的宽度即可.
【解答】解:建立如图所示的直角坐标系,
设抛物线解析式为y=ax2+c,
把(2,0)和(0,2)代入得,
,
解得,
∴抛物线解析式为yx2+2,
把y=0.5代入得:x=±,
则水面的宽度是2米.
故答案为:2.
【点评】此题考查了二次函数的应用,熟练掌握待定系数法是解本题的关键.
7.(2024 城中区校级一模)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 45 m.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】45.
【分析】根据二次函数的解析式找出其顶点式,再利用二次函数的性质求出s的最大值即可得出结论.【解答】【点评】
【解答】解:∵s=﹣5t2+30t=﹣5(t﹣3)2+45,
∴汽车刹车后到停下来前进了45m,
故答案为:45.
【点评】本题考查了二次函数的应用,利用配方法,求出二次函数的顶点式是解题的关键.
8.(2024 长春一模)为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 7 米.
【考点】二次函数的应用.
【专题】数形结合;待定系数法;一元二次方程及应用;二次函数图象及其性质;二次函数的应用;几何直观;运算能力;应用意识.
【答案】见试题解答内容
【分析】建立坐标系,设抛物线的解析式为y=a(x﹣2)2+2,由待定系数法求得抛物线的解析式,令y=0,得关于x的一元二次方程,求得方程的解并根据问题的实际意义作出取舍即可.
【解答】解:建立坐标系,如图所示:
由题意得:A(0,1.68),B(2,2),点B为抛物线的顶点,
设抛物线的解析式为y=a(x﹣2)2+2,
把A(0,1.68)代入得:
4a+2=1.68,
解得a=﹣0.08,
∴y=﹣0.08(x﹣2)2+2,
令y=0,得﹣0.08(x﹣2)2+2=0,
解得x1=7,x2=﹣3(舍),
∴小丁此次投掷的成绩是7米.
故答案为:7.
【点评】本题考查了二次函数在实际问题中的应用,正确建立平面直角坐标系、熟练掌握待定系数法及二次函数与一元二次方程的关系是解题的关键.
9.(2024 高邑县期末)一座抛物线型拱桥如图所示,桥下水面宽度是4m时,拱顶距离水面是2m.当水面下降1m后,水面宽度是 2 m.(结果保留根号)
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】2.
【分析】根据题意,建立合适的平面直角坐标系,然后求出抛物线的解析式,再将y=﹣3代入函数解析式,求出x的值,然后即可求得水面下降1m后,水面宽度.
【解答】解:建立平面直角坐标系,如图所示,
设该抛物线的解析式为y=ax2,
由题意可知:点(2,﹣2)在该函数图象上,
∴﹣2=a×22,
解得a,
∴该抛物线的解析式为yx2,
当y=﹣3时,﹣3x2,
解得x1,x2,
∴当水面下降1m后,水面宽度是:()2(m),
故答案为:2.
【点评】本题考查二次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式.
10.(2024 光山县校级开学)有一长方形条幅,长为am,宽为bm,四周镶上宽度相等的花边,则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为 s=(a﹣2x)(b﹣2x) ,自变量x的取值范围为 0<x .
【考点】根据实际问题列二次函数关系式.
【答案】见试题解答内容
【分析】因为四周镶上宽度相等的花边,所以剩余长方形的长为(a﹣2x),宽为(b﹣2x),利用长方形的面积公式:长×宽,可表示出函数关系式;2x应该小于宽b,可求得x的上限,下限为x>0,所以可求出自变量x的取值范围.
【解答】解:剩余长方形的长为(a﹣2x),宽为(b﹣2x),
则剩余面积S(m2)与花边宽度x(m)之间的函数关系式为:s=(a﹣2x)(b﹣2x).
∵x>0,2x<b
∴自变量x的取值范围为0<x.
故答案为:s=(a﹣2x)(b﹣2x);0<x.
【点评】主要考查了二次函数的实际运用.用含x的代数式表示出长和宽,再根据长方形的面积公式即可表示出二次函数的解析式.
三.解答题(共5小题)
11.(2024 宣化区期末)2023年杭州亚运会吉祥物一开售,就深受大家的喜爱.某旅游商店以每件50元的价格购进某款亚运会吉祥物,以每件80元的价格出售,每日可售出200件.从7月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该吉祥物每降价1元,日销售量就会增加20件.
(1)设定价为x元,日销售量为y件.试用含x的式子表示y,y= ﹣20x+1800 ;
(2)当该吉祥物售价为多少元时,日销售利润达7500元?
(3)请你测算一下,该商场如何定价,可使日销售利润最多?
【考点】二次函数的应用;一元二次方程的应用.
【专题】二次函数的应用;运算能力.
【答案】见试题解答内容
【分析】(1)销售量=降价前每日销售量+降价所增加的销售量,据此即可求解;
(2)每件所获利润×日销售量=7500元,据此即可求解;
(3)设日销售利润为W元,日销售利润=每件所获利润×日销售量,据此即可求解.
【解答】解:(1)y=200+20(80﹣x)
=﹣20x+1800,
故答案为:﹣20x+1800;
(2)由题意得:
(x﹣50)(﹣20x+1800)=7500,
整理得:x2﹣140x+4875=0,
解得:x1=65,x2=75,
∵降价促销,
∴x2=75舍去,
∴x=65,
答:该吉祥物售价为65元时,日销售利润达7500元.
(3)设日销售利润为W元,由题意得:
W=(x﹣50)(﹣20x+1800)
=﹣20(x﹣70)2+8000,
∵﹣20<0,
∴当x=70时,W最大=8000(元);
答:每件售价为70元时,可使日销售利润最多.
【点评】本题考查一次函数在销售问题的应用,一元二次方程在销售问题中应用,二次函数在销售问题中的应用,找出等量关系式是解题的关键.
12.(2024 陇西县期末)中国茶文化是中国传统文化的重要组成部分之一,代表了中国文化的精髓和卓越,具有丰富的文化内涵和深远的历史意义.某茶庄经销一种绿茶,每千克成本为50元,经市场调查发现:在一段时间内,销售量W(千克)随销售单价x(元/千克)的变化而变化,具体关系式为W=﹣2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x之间的函数关系式;
(2)当绿茶的销售单价是多少时,该茶庄这种绿茶在这段时间内的销售利润最大?最大利润是多少?
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)y=﹣2x2+340x﹣12000;
(2)当绿茶的销售单价是85元/千克时,该茶庄这种绿茶在这段时间内的销售利润最大,最大利润是2450元.
【分析】(1)根据销售利润=销量×(销售单价﹣每千克成本)可求出关系式;
(2)用配方法或公式法来求二次函数最大值的问题.
【解答】解:(1)y=(x﹣50) W=(x﹣50)(﹣2x+240)=﹣2x2+340x﹣12000,
∴y与x之间的函数关系式为:y=﹣2x2+340x﹣12000.
(2)y=﹣2x2+340x﹣12000=﹣2(x﹣85)2+2450,
∴当x=85时,y的值最大,最大为2450元.
即当绿茶的销售单价是85元/千克时,该茶庄这种绿茶在这段时间内的销售利润最大,最大利润是2450元.
【点评】本题主要考查了二次函数的应用,解决本题的关键要找出等量关系,列出二次函数解析式,用配方法或公式法来求二次函数最大值.
13.(2024 凉州区三模)如图1所示是一座古桥,桥拱截面为抛物线,如图2,AO,BC是桥墩,桥的跨径AB为20m,此时水位在OC处,桥拱最高点P离水面6m,在水面以上的桥墩AO,BC都为2m.以OC所在的直线为x轴、AO所在的直线为y轴建立平面直角坐标系,其中x(m)是桥拱截面上一点距桥墩AO的水平距离,y(m)是桥拱截面上一点距水面OC的距离.
(1)求此桥拱截面所在抛物线的表达式;
(2)有一艘游船,其左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在河中航行.当水位上涨2m时,水面到棚顶的高度为3m,遮阳棚宽12m,问此船能否通过桥洞?请说明理由.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)此桥拱截面所在抛物线的表达式为;
(2)此船不能通过桥洞.理由见解析.
【分析】(1)先求出点A,点B,点P的坐标,再把抛物线解析式设为顶点式进行求解即可;
(2)求出当y=5时x的值,然后计算出两个对应的x的值之间的差的绝对值即可得到答案.
【解答】解:(1)由题意知,A(0,2),P(10,6),B(20,2),
设抛物线解析式为y=a(x﹣10)2+6,
把A(0,2)代入解析式得,100a+6=2,
解得,
∴此桥拱截面所在抛物线的表达式为;
(2)此船不能通过,理由:
当y=2+3=5时,,
解得x=5或x=15,
∵15﹣5=10<12,
∴此船不能通过桥洞.
【点评】本题考查二次函数的应用,熟练掌握二次函数的图象与性质是解本题的关键【点睛】本题考查二次函数的应用,熟练掌握二次函数的图象与性质是解本题的关键.
14.(2024 右玉县四模)某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) 1月 2月 3月 4月 5月 6月
销售量(p) 3.9万台 4.0万台 4.1万台 4.2万台 4.3万台 4.4万台
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
【考点】二次函数的应用.
【答案】见试题解答内容
【分析】(1)直接利用待定系数法求一次函数解析式即可;
(2)利用销量×售价=销售金额,进而利用二次函数最值求法求出即可;
(3)分别表示出1,2月份的销量以及售价,进而利用今年2月份这种品牌手机的销售额为6400万元,得出等式求出即可.
【解答】解:(1)设p=kx+b,
把p=3.9,x=1;p=4.0,x=2分别代入p=kx+b中,
得:,
解得:,
∴p=0.1x+3.8;
(2)设该品牌手机在去年第x个月的销售金额为w万元,
w=(﹣50x+2600)(0.1x+3.8)
=﹣5x2+70x+9880
=﹣5(x﹣7)2+10125,
当x=7时,w最大=10125,
答:该品牌手机在去年七月份的销售金额最大,最大为10125万元;
(3)当x=12时,y=2000,p=5,
1月份的售价为:2000(1﹣m%)元,则2月份的售价为:0.8×2000(1﹣m%)元;
1月份的销量为:5×(1﹣1.5m%)万台,则2月份的销量为:[5×(1﹣1.5m%)+1.5]万台;
∴0.8×2000(1﹣m%)×[5×(1﹣1.5m%)+1.5]=6400,
解得:m1%(舍去),m2%,
∴m=20,
答:m的值为20.
【点评】此题主要考查了二次函数的应用以及待定系数法求一次函数解析式,根据题意表示出2月份的销量与售价是解题关键.
15.(2024 满城区期末)鹰眼技术助力杭州亚运,提升球迷观赛体验.如图分别为足球比赛中某一时刻的鹰眼系统预测画面(如图1)和截面示意图(如图2),攻球员位于点O,守门员位于点A,OA的延长线与球门线交于点B,且点A,B均在足球轨迹正下方,足球的飞行轨迹可看成抛物线.水平距离s与离地高度h的鹰眼数据如表:
s/m … 9 12 15 18 21 …
h/m … 4.2 4.8 5 4.8 4.2 …
(1)根据表中数据预测足球落地时,s= 30 m;
(2)求h关于s的函数解析式;
(3)当守门员位于足球正下方,足球离地高度不大于守门员的最大防守高度2.6m时,视为防守成功.若一次防守中,守门员位于足球正下方时,s=24m,请问这次守门员能否防守成功?试通过计算说明.
【考点】二次函数的应用.
【专题】二次函数图象及其性质;二次函数的应用;运算能力.
【答案】见试题解答内容
【分析】(1)根据抛物线的对称轴可直接得出结论;
(2)根据抛物线的对称性找到顶点,设出顶点式,再代入(12,4.8)可求出参数,由此可解答;
(3)根据s的值,求出h,再与最大防守高度2.6m比较即可.
【解答】解:(1)由表格可知,s=9时和s=21时,h相等,s=12时,s=18时,h相等,
抛物线关于s=15对称,
∵当s=0时,h=0,
∴s=30时,h=0,
故答案为:30.
(2)由(1)知,抛物线关于s=15对称,设h=a(s﹣15)2+5,
把(12,4.8)代入上述解析式,
∴a(12﹣15)2+5=4.8,解得a,
∴h(s﹣15)2+5,
即hs2s;
(3)不能防守成功,
理由如下:当s=24m时,hs2s24224=3.2(m),
∵3.2>2.6,
∴这次守门员不能防守成功.
【点评】本题考查二次函数的实际应用,理解题意,掌握抛物线的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
