人教版七年级数学上册 第三章 代数式 全章教案
文档属性
| 名称 | 人教版七年级数学上册 第三章 代数式 全章教案 | 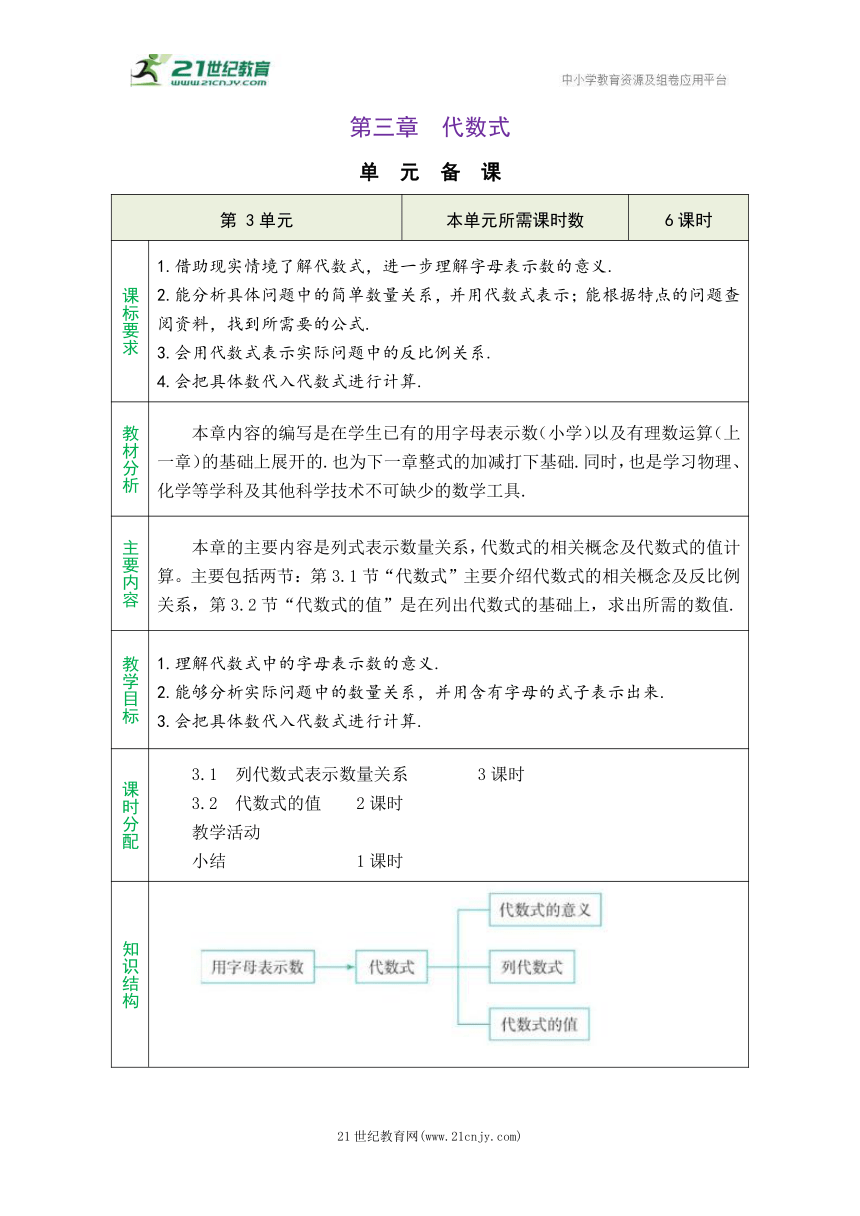 | |
| 格式 | docx | ||
| 文件大小 | 109.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 05:31:03 | ||
图片预览





文档简介
第三章 代数式
单 元 备 课
第 3单元 本单元所需课时数 6课时
课标要求 1.借助现实情境了解代数式,进一步理解字母表示数的意义. 2.能分析具体问题中的简单数量关系,并用代数式表示;能根据特点的问题查阅资料,找到所需要的公式. 3.会用代数式表示实际问题中的反比例关系. 4.会把具体数代入代数式进行计算.
教材分析 本章内容的编写是在学生已有的用字母表示数(小学)以及有理数运算(上一章)的基础上展开的.也为下一章整式的加减打下基础.同时,也是学习物理、化学等学科及其他科学技术不可缺少的数学工具.
主要内容 本章的主要内容是列式表示数量关系,代数式的相关概念及代数式的值计算。主要包括两节:第3.1节“代数式”主要介绍代数式的相关概念及反比例关系,第3.2节“代数式的值”是在列出代数式的基础上,求出所需的数值.
教学目标 1.理解代数式中的字母表示数的意义. 2.能够分析实际问题中的数量关系,并用含有字母的式子表示出来. 3.会把具体数代入代数式进行计算.
课时分配 3.1 列代数式表示数量关系 3课时 3.2 代数式的值 2课时 教学活动 小结 1课时
知识结构
教与学建议 1.加强式与数的类比教学. 2.重视培养学生列式表示数量关系的能力. 3.抓住重点、加强练习,打好基础.
3.1 列代数式表示数量关系
第1课时 代数式
课题 代数式 课型 新授课
教学内容 教材第69-71页的内容
教学目标 1.结合具体情境,认识并学会用字母表示数及含有字母的式子. 2.经历用字母或含有字母的式子表示数的探索过程,把文字语言转化为符号语言,用数学的语言刻画实际问题. 3.理解并掌握代数式的定义及意义.
教学重难点 教学重点:理解并掌握代数式的定义. 教学难点:进一步理解代数式的意义.
教 学 过 程 备 注
1.创设情境,引入课题 智能机器人的广泛应用是智慧农业的发展趋势之一.科技给农业提供了更多的便利.(展示图片,并结合图片说明.) 2.类比探究,学习新知 【问题1】智能机器人的广泛应用是智慧农业的发展趋势之一.某品牌苹果采摘机器人可以1 s完成5 m2范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手8 s可以采摘一个苹果.根据这些数据回答下列问题: (1)该机器人10 s能识别多大范围内的苹果?60 s呢?t s呢? (2)该机器人识别n m2范围内的苹果需要多少秒? (3)若该机器人搭载了10个机械手,它与采摘工人同时工作1 h,假设工人m s可以采摘一个苹果,则机器人可比工人多采摘多少个苹果? (4)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗? 【师生活动】师生共同解答问题. 【归纳】用字母t表示时间,字母t可以像数一样参与运算,并且可以简明表示机器人能识别多大范围内的苹果数.与字母相乘或字母与字母相乘,通常将乘号写作“”或省略不写. 【问题2】分析数量关系,并用含有字母的式子表示数量关系: (1)一个正方形的边长是a,这个正方形的周长和面积是多少? (2)某工程队铺设一条长3m的管道,t天完成,这支工程队平均每天铺设多少管道? 【师生活动】学生先独立列式,然后同桌交流,学生代表板演展示,教师巡视指导. 教师提问上述问题中列出的式子,有什么共同点? 共同归纳:它们都是用运算符号把数或表示数的字母连接起来的式子,我们称这样的式子为代数式. 单独的一个数或字母也是代数式. 用字母表示数后,同一个代数式可以表示不同实际问题中的数量或数量关系. 3.学以致用,应用新知 【例】列代数式表示数量关系: (1)苹果原价是每千克p元,按9折优惠出售,用代数式表示苹果的售价; (2)一个长方形的长是0.9 m,宽是p m,用代数式表示这个长方形的面积; (3)某产品前年的产量是n件,去年的产量比前年产量的2倍少10件,用代数式表示去年的产量; (4)一个长方体水池底面的长和宽都是a m,高是h m,池内水的体积占水池容积的三分之一,用代数式表示池内水的体积. 解:(1)苹果的售价是每千克0.9p元. (2)这个长方形的面积是0.9p m. (3)去年的产量是(2n-10)件. (4)由长方体的体积=长×宽×高,得这个长方形水池的容积是a·a·h m3,即a2h m3,故池内水的体积为a2h m3. 4.随堂训练,巩固新知 1.(1)每包书有10册,6包书有 册,n包书有 册; (2)王芳今年m岁,她去年 岁,6年后 岁; (3)将p kg糖装入n个包装袋中,每袋糖的质量相同,每袋装入糖 kg; (4)棱长为a的正方形的体积是 . 2.说出下列代数式的意义: (1)2a+3c;(2)3(m-n);(3)a2+1;(4)3a/5b. 答案:1.60,10n,m-1,m+6,np,a3. 2.(1)a的2倍与c的3倍的和; (2)m与n的差的3倍; (3)a的平方与1的和; (4)a的3倍除以b的5倍的商. 5.课堂小结,自我完善 (1)什么叫作代数式?用代数式表示数量关系有什么意义? (2)用代数式表示数量关系时要注意什么? 6.布置作业 课本P71练习1-3,P75习题3.1第1,2,7题. 通过展示图片,吸引学生注意力,激发学生的民族自豪感,引出下面的问题. 让学生经历由数到式的过程,感受从特殊(具体)到一般(抽象)的认识过程,体会用字母表示数的简洁性和必要性,为下面继续学习用含有字母的式子表示数量关系做好方法上的引导. 通过观察、比较、讨论,归纳出代数式的概念,提高学生的归纳能力. 进一步熟悉用含有字母的式子表示实际问题中的数量关系,体会字母的含义,进一步理解字母可以像数一样参与运算,为形成代数式的概念进行铺垫. 进一步理解字母表示数的意义,理解用代数式表示实际问题中数量关系的简洁性、必要性和一般性. 通过小结,使学生梳理本节课所学内容.
板书设计 代数式的意义 代数式: 用运算符号把数或表示数的字母连接起来的式子称为代数式. 单独的一个数或字母也是代数式. 2.列式的注意事项: (1)数与字母、字母和字母相乘省略乘号; (2)数与字母相乘时数字写在前面. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
第2课时 列代数式
课题 列代数式 课型 新授课
教学内容 教材第71-73页的内容
教学目标 1.会用代数式表示实际问题中的数量关系. 2.初步培养抽象能力、应用意识.
教学重难点 教学重点:熟练运用代数式表示实际问题中的数量关系. 教学难点:熟练运用代数式表示实际问题中的数量关系.
教 学 过 程 备 注
1.创设情境,引入课题 我们知道字母可以表示数,在解决问题时常需要把问题中与数量有关的词语用代数式表示出来,本节我们就来探究如何列代数式. 思考:如何用代数式表示a,b两数的和与差的积? 【师生活动】学生尝试解答,教师引导将问题分解成表示a,b两数的和,表示a,b两数的差,再表示它们的积三个问题,从而列出最终的代数式. 2.类比探究,学习新知 【问题1】列代数式:(1)一条河的水流速度为2.5 km/h,船在静水中的速度为v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度; (2)一个正方体的棱长是a,这个正方体的表面积是多少?体积呢? 【师生活动】学生先独立列式,然后同桌交流,学生代表板演展示,教师巡视指导. 解:(1)顺水行驶和逆水行驶时的速度分别是(v+2.5)km/h,(v-2.5)km/h; (2)面积=6a2,体积=a3. 归纳:(1)列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.分析实际问题时应注意:①抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;②理清语句层次,明确运算顺序;③联想相关概念和公式. (2)列式书写时应注意:①数与字母、字母与字母相乘省略乘号;②数与字母相乘时数字在前;③式子中出现除法运算时,一般按分数形式来写;④带分数与字母相乘时,把带分数化成假分数;⑤带单位时,适当加括号. 【问题2】上面的问题中,既有已知数,又有用字母表示的数,字母表示数有什么意义?用含有字母的代数式表示数量关系有什么意义? 【师生活动】学生尝试回答,教师根据学生回答情况进行评价. 归纳;用字母表示数,字母和数一样可以参与运算,可以用代数式把数量关系简明地表示出来. 3.学以致用,应用新知 【例】用代数式表示: 购买2个单价为a元的面包和3瓶单价为b元的饮料所需的钱数; 爸爸把a元钱存入银行,存期3年,年利率为2.75%,到期时的利息是多少元?; 某商品的进价为x元,先按进价的1.1倍标价,后又降价80元出售,现在的售价是多少元? 答案:(1)(2a+3b)元;(2)8.25%a元; (3)(1.1x-80)元. 4.随堂训练,巩固新知 1.用代数式表示: (1)比a的2倍大1的数; (2)a的相反数与b的一半的差; (3)a的平方除以b的商. 答案:(1)2a+1; (2)(-a)- b/2; (3)a2/b. 2.一列数1,4,7,10,13……按此规律排列,第n个数是 . 答案:3n-2 5.课堂小结,自我完善 (1)怎样列代数式? (2)列代数式时需要注意什么? (3)你还有什么疑惑? 6.布置作业 课本P73练习1-4. 利用分解问题降低难度的方式帮助学生分析问题、解决问题,为接下来的学习打下基础. 由浅入深,使学生透彻理解代数式的表示,培养学生的符号意识,培养他们应用新知识解决问题的能力. 进一步理解字母表示数的意义,理解用代数式表示实际问题中数量关系的简洁性、必要性和一般性. 例题的讲解,让学生巩固所学的新知识. 进一步巩固新知,及时检测学习效果. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 列代数式 1. 列简单的代数式 2. 根据实际问题列代数式 例 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
第3课时 反比例关系
课题 反比例关系 课型 新授课
教学内容 教材第73-75页的内容
教学目标 1.分析实际问题中两个量之间的变化,理解反比例关系,并用式子表示反比例关系. 2. 培养函数思想和数学建模能力,能用函数的观点分析、解决实际问题.
教学重难点 教学重点: 反比例关系及表示. 教学难点:从实际问题中抽象出数学问题,建立数学模型.
教 学 过 程 备 注
1.创设情境,引入课题 回顾本章引言中的问题(1).机器人t s能识别的范围是5t m2,也就是说机器人能识别的范围与所用时间的比例总是一定的(等于5).因此机器人能识别的范围与所用时间是成正比例的量,它们成正比例关系. 对于工程问题,如果工作量保持不变,工作时间与工作效率之间又有怎样的关系呢? 师生活动:由学生小组合作交流,教师肯定每一位学生说出的特点. 2.类比探究,学习新知 【问题1】北京是全球首个既举办过夏季奥运会又举办过冬季运动会的城市.在冬季奥运会前,某赛场计划造雪260 000 m3.解答下列问题: (1)根据每天造雪量,计算所需的造血天数,填写下表. 每天造雪量/m35 0005 2006 500...造雪天数...
(2)每天造雪量和造血天数这两个量是怎样变化的?它们之间有什么关系? 【师生活动】教师引导学生分析,此问题包含的三个量分别为造雪总量、每天造雪量和造雪天数,它们之间的关系为造雪总量=每天造雪量×造雪天数. 师生共同归纳:像这样,两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,这两个量就叫作成反比例的量,它们之间的关系叫作反比例关系. 【问题2】如何用式子表示反比例关系? 【师生活动】 师生共同总结:如果用字母x和y表示两个相关联的量,用k表示它们的积(k是一个确定的值,且k≠0),反比例关系可以用xy=k来表示. 3.学以致用,应用新知 【例】已知四个圆柱形容器内部的底面积分别为10cm2,20cm2,30cm2,60cm2.分别往这四个容器中注入300cm3的水. (1)四个容器中水的高度分别是多少厘米? (2)分别用x(单位:cm2)和y(单位:cm)表示容积内部的底面积与水的高度,用式子表示y与x的关系,y与x成什么比例关系? 答案: 4.随堂训练,巩固新知 1.汽车从甲地驶往乙地,汽车行驶的平均速度与时间是否成反比例关系?为什么? 答案:成反比例关系.路程一定,路程=速度×时间, 时间随速度的增大而减小. 2.长方体的体积一定,长方体的底面积与高是否成反比例关系?为什么? 答案:成反比例关系.体积一定,体积=底面积×高, 高随底面积的增大而减小. 3.某运输公司计划运输一批货物,每天运输的吨数与运输的天数之间的关系如下表: 每天运输的吨数50025010050...运输的天数12510...
(1)这批货物共有多少吨? (2)运输的天数是怎样随着每天运输的吨数的变化而变化的? (3)用t表示运输的天数,用a表示每天运输的吨数,用式子表示t与a的关系.t与a成什么比例关系? 答案:(1)这批货物共有500 吨; (2)运输的天数随着每天运输的吨数的减少而增加; (3)500=at,成反比例关系. 5.课堂小结,自我完善 (1)什么是反比例关系? (2)怎么用式子表示反比例关系? 6.布置作业 课本P75练习. 通过简单的复习正比例的相关概念,为探究、学习反比例的相关概念打下坚实的基础. 以问题串的形式创设情境,引起学生的认知冲突,使学生对新知识产生好奇,从而激发学生的学习兴趣和求知欲望. 结合实际,体会成反比例关系的两个量之间的依存关系,体会反比例关系在实际生活中的应用. 巩固反比例关系的概念,使学生体会到数学来源于生活,应用于生活的价值美. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 反比例关系 1.反比例关系 2.表示:xy=k(k是一个确定的值,且k≠0) 例 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
3.2 代数式的值
第1课时 求代数式的值
课题 求代数式的值 课型 新授课
教学内容 教材第79-80页的内容
教学目标 1.会求代数式的值. 2.培养运算能力及分析问题、解决问题的能力.
教学重难点 教学重点: 在解决具体问题时,熟练求出代数式的值. 教学难点: 在解决具体问题时,熟练求出代数式的值.
教 学 过 程 备 注
1.创设情境,引入课题 为了开展体育活动,学校要购置一批排球,每班配5个,学校另外留20个.学校总共需要购置多少个排球? 【师生活动】学生尝试解答,记全校的班级数是n,需要购置的排球总数是 5n+20. 2.类比探究,学习新知 【问题1】上述问题中,如果班级数是15,那么需要购置多少个排球? 如果班级数是20呢? 【师生活动】学生尝试解答.如果班级数是15,用15代替字母n,那么需要购置的排球总数是5n+20=5×15+20=95;如果班级数是20,用20代替字母n,那么需要购置的排球总数是5n+20=5×20+20=120. 总结:一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同. 3.学以致用,应用新知 【例1】根据下列x,y的值,分别求代数式2x+3y的值: (1)x=15,y=12;(2)x=1,y=. 答案:(1)当x=15时,y=12时, 2x+3y=2×15+3×12=66; (2)当x=1,y=时,2x+3y=2×1+3×=. 【例2】根据下列a,b的值,分别求代数式a2 的值; (1)a=4,b=12;(2)a=-3,b=2. 答案:(1)当a=4,b=12时,a2 =42-=13; (2)当a=-3,b=2时,a2 =(-3)2- = . 【例3】冰糖葫芦是我国传统小吃,若有a个山楂,按每串冰糖葫芦的山楂个数相等的规定,穿了b串冰糖葫芦,还剩余c个山楂,则每串冰糖葫芦的山楂个数是多少?当a=150,b=18,c=6时,求每串冰糖葫芦的山楂个数. 解:每串冰糖葫芦的山楂个数是. 当a=150,b=18,c=6时,. 即每串冰糖葫芦的山楂个数是8. 4.随堂训练,巩固新知 1.当x=﹣1时,则代数式x+4的值为( ) A.5 B.﹣3 C.3 D.﹣5 答案:C 2.已知m=﹣2,n=1,则代数式n﹣m的值为( ) A.2 B.﹣2 C.﹣3 D.3 答案:D 3. 已知代数式2a2b+3ab﹣4,当a=﹣3,b=﹣2时,求m的值. 答案:当a=﹣3,b=﹣2时,2a2b+3ab﹣4 =2×(﹣3)2×(﹣2)+3×(﹣3)×(﹣2)﹣4 =2×9×(﹣2)+3×(﹣3)×(﹣2)﹣4 =﹣36+18﹣4 =﹣22. 4. 当x=2,y=-3时,求代数式x2+2xy+y2的值. 答案:当x=2,y=-3时, x2+2xy+y2=22+2×2×( 3)+( 3)2=1. 5.课堂小结,自我完善 (1)如何求代数式的值? (2)求代数式的值时,需要注意什么? 6.布置作业 课本P80练习1-3,P82习题3.2第1,3,4题. 引入实际问题,使学生感受到学习代数式的值的运算是实际需要.此环节教师应关注学生是否能正确列式,得出正确的式子. 通过让学生解决生活中的实际问题,进一步理解代数式的值,培养计算能力,激发学习兴趣. 让学生进一步了解代数式的值的意义,提高学生的数学运算能力. 通过练习加深对本节课内容的理解. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 求代数式的值 一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
第2课时 列代数式求值
课题 列代数式求值 课型 新授课
教学内容 教材第80-81页的内容
教学目标 1.熟练掌握几何图形公式,根据实际问题列代数式并求值. 2.通过现实问题情境进一步理解用字母表示数的意义.
教学重难点 教学重点:根据实际问题列代数式求值. 教学难点:根据实际问题列代数式求值.
教 学 过 程 备 注
1.创设情境,引入课题 有些同类事物中的数量关系常常可以用公式来描还,例如,在行程问题中,用s表示路程,v表示速度,t表示时间,就可以得到路程公式s=vt,它表示了路程、速度、时间这三个量之间的关系.知道v,t的值,就可以利用公式求出s的值.在小学,我们学习过许多公式,如长方形、正方形、三角形、梯形、圆等图形的面积公式,长方体、正方体等图形的体积公式,等等.在解决有关问题时,经常用这些公式进行计算. 2.类比探究,学习新知 【问题1】某学校操场最内测的跑道由两段直道和两端半圆形的弯道组成,其中直道的长为a,半圆形弯道的直径为b. (1)用代数式表示这条跑道的周长; (2)当a=67.3 m,b=52.6 m时,求这条跑道的周长(π取3.14,结果取整数). 【师生活动】学生尝试解答.(1)两条直道的长度为2a,两端半圆形弯道可以看成一个圆,其周长为πb,所以跑道的周长为2a+πb. (2)当a=67.3 m,b=52.6 m时, 2a+πb=2×67.3+3.14×52.6≈300(m). 因此,这条跑道的周长约为300 m. 教师强调:本题中用到了圆的周长公式,对于长方形、正方形、三角形、圆等的周长、面积公式要熟练掌握.根据实际问题列出代数式,再用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果. 3.学以致用,应用新知 【例】如图,公园有一个“T”型空地(即阴影部分,单位:米). (1)用含x,y的代数式表示空地的面积;(结果要进行化简) (2)公园管理部门计划对空地铺设草坪.已知每平方米草坪的费用为200元,若x,y满足(x﹣3)2+|y﹣5|=0,求铺设草坪的总费用. 解:(1)2x(2x+2y)+2xy =(4x2+6xy)m2. (2)由(x﹣3)2+|y﹣5|=0,可得x=3,y=5. 将x=3,y=5代入4x2+6xy,得 原式=4×32+6×3×5=126(m2). 所以铺设草坪的总费用是:126×200=25200元. 4.随堂训练,巩固新知 1.一个长方体纸箱的长是a,宽与高都是b,这个纸箱的体积V是多少?如果a=60 cm,b=40 cm,求V的值. 答案:V=ab2,当a=60 cm,b=40 cm时,V=96 000 cm3. 2. 如图长方形的长为a,宽为2b, (1)用含a、b的式子表示图中阴影部分的面积S. (2)当a=5cm,b=2cm时,求阴影部分面积S的值.(其中π取3.14) 答案:解:(1)∵长方形的长为a,宽为2b, ∴S阴影=2ab﹣πb2; (2)a=5cm,b=2cm时, S阴影=20﹣3.14×4=7.44(cm2), 即S阴影=7.44(cm2). 3. 如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米) (1)用含a,b的整式表示花坛的面积; (2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元? 答案:(1)(a+3b+a)(2a+b)﹣2a 3b =4a2+8ab+3b2﹣6ab =(4a2+2ab+3b2)m2. 答:花坛的面积是(4a2+2ab+3b2)m2. (2)当a=4,b=3时, 4a2+2ab+3b2 =4×42+4×2×3+3×32 =115(m2), 115×500=57500(元). 答:建花坛的总工程费为57500元. 5.课堂小结,自我完善 (1)本节你学到了什么?试着总结一下. (2)除了今天学习的公式,还有哪些公式可以用来描述实际问题中的数量关系? 6.布置作业 课本P81练习1-3,P82习题3.2第6题. 引导学生回忆学过的几何公式,感受到代数式与几何公式和实际生活的密切联系.此环节教师应关注学生是否能正确列式,得出正确的式子. 鼓励学生自主探索,体会用公式解决数学问题的方法. 通过让学生解决生活中的实际问题,进一步理解代数式的值,培养计算能力,激发学习兴趣. 通过练习加深对本节内容的理解,使学生感受“数式通性”及用公式描述数量关系的抽象过程. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 列代数式求值 常用的数学公式 例 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
21世纪教育网(www.21cnjy.com)
单 元 备 课
第 3单元 本单元所需课时数 6课时
课标要求 1.借助现实情境了解代数式,进一步理解字母表示数的意义. 2.能分析具体问题中的简单数量关系,并用代数式表示;能根据特点的问题查阅资料,找到所需要的公式. 3.会用代数式表示实际问题中的反比例关系. 4.会把具体数代入代数式进行计算.
教材分析 本章内容的编写是在学生已有的用字母表示数(小学)以及有理数运算(上一章)的基础上展开的.也为下一章整式的加减打下基础.同时,也是学习物理、化学等学科及其他科学技术不可缺少的数学工具.
主要内容 本章的主要内容是列式表示数量关系,代数式的相关概念及代数式的值计算。主要包括两节:第3.1节“代数式”主要介绍代数式的相关概念及反比例关系,第3.2节“代数式的值”是在列出代数式的基础上,求出所需的数值.
教学目标 1.理解代数式中的字母表示数的意义. 2.能够分析实际问题中的数量关系,并用含有字母的式子表示出来. 3.会把具体数代入代数式进行计算.
课时分配 3.1 列代数式表示数量关系 3课时 3.2 代数式的值 2课时 教学活动 小结 1课时
知识结构
教与学建议 1.加强式与数的类比教学. 2.重视培养学生列式表示数量关系的能力. 3.抓住重点、加强练习,打好基础.
3.1 列代数式表示数量关系
第1课时 代数式
课题 代数式 课型 新授课
教学内容 教材第69-71页的内容
教学目标 1.结合具体情境,认识并学会用字母表示数及含有字母的式子. 2.经历用字母或含有字母的式子表示数的探索过程,把文字语言转化为符号语言,用数学的语言刻画实际问题. 3.理解并掌握代数式的定义及意义.
教学重难点 教学重点:理解并掌握代数式的定义. 教学难点:进一步理解代数式的意义.
教 学 过 程 备 注
1.创设情境,引入课题 智能机器人的广泛应用是智慧农业的发展趋势之一.科技给农业提供了更多的便利.(展示图片,并结合图片说明.) 2.类比探究,学习新知 【问题1】智能机器人的广泛应用是智慧农业的发展趋势之一.某品牌苹果采摘机器人可以1 s完成5 m2范围内苹果的识别,并自动对成熟的苹果进行采摘,它的一个机械手8 s可以采摘一个苹果.根据这些数据回答下列问题: (1)该机器人10 s能识别多大范围内的苹果?60 s呢?t s呢? (2)该机器人识别n m2范围内的苹果需要多少秒? (3)若该机器人搭载了10个机械手,它与采摘工人同时工作1 h,假设工人m s可以采摘一个苹果,则机器人可比工人多采摘多少个苹果? (4)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗? 【师生活动】师生共同解答问题. 【归纳】用字母t表示时间,字母t可以像数一样参与运算,并且可以简明表示机器人能识别多大范围内的苹果数.与字母相乘或字母与字母相乘,通常将乘号写作“”或省略不写. 【问题2】分析数量关系,并用含有字母的式子表示数量关系: (1)一个正方形的边长是a,这个正方形的周长和面积是多少? (2)某工程队铺设一条长3m的管道,t天完成,这支工程队平均每天铺设多少管道? 【师生活动】学生先独立列式,然后同桌交流,学生代表板演展示,教师巡视指导. 教师提问上述问题中列出的式子,有什么共同点? 共同归纳:它们都是用运算符号把数或表示数的字母连接起来的式子,我们称这样的式子为代数式. 单独的一个数或字母也是代数式. 用字母表示数后,同一个代数式可以表示不同实际问题中的数量或数量关系. 3.学以致用,应用新知 【例】列代数式表示数量关系: (1)苹果原价是每千克p元,按9折优惠出售,用代数式表示苹果的售价; (2)一个长方形的长是0.9 m,宽是p m,用代数式表示这个长方形的面积; (3)某产品前年的产量是n件,去年的产量比前年产量的2倍少10件,用代数式表示去年的产量; (4)一个长方体水池底面的长和宽都是a m,高是h m,池内水的体积占水池容积的三分之一,用代数式表示池内水的体积. 解:(1)苹果的售价是每千克0.9p元. (2)这个长方形的面积是0.9p m. (3)去年的产量是(2n-10)件. (4)由长方体的体积=长×宽×高,得这个长方形水池的容积是a·a·h m3,即a2h m3,故池内水的体积为a2h m3. 4.随堂训练,巩固新知 1.(1)每包书有10册,6包书有 册,n包书有 册; (2)王芳今年m岁,她去年 岁,6年后 岁; (3)将p kg糖装入n个包装袋中,每袋糖的质量相同,每袋装入糖 kg; (4)棱长为a的正方形的体积是 . 2.说出下列代数式的意义: (1)2a+3c;(2)3(m-n);(3)a2+1;(4)3a/5b. 答案:1.60,10n,m-1,m+6,np,a3. 2.(1)a的2倍与c的3倍的和; (2)m与n的差的3倍; (3)a的平方与1的和; (4)a的3倍除以b的5倍的商. 5.课堂小结,自我完善 (1)什么叫作代数式?用代数式表示数量关系有什么意义? (2)用代数式表示数量关系时要注意什么? 6.布置作业 课本P71练习1-3,P75习题3.1第1,2,7题. 通过展示图片,吸引学生注意力,激发学生的民族自豪感,引出下面的问题. 让学生经历由数到式的过程,感受从特殊(具体)到一般(抽象)的认识过程,体会用字母表示数的简洁性和必要性,为下面继续学习用含有字母的式子表示数量关系做好方法上的引导. 通过观察、比较、讨论,归纳出代数式的概念,提高学生的归纳能力. 进一步熟悉用含有字母的式子表示实际问题中的数量关系,体会字母的含义,进一步理解字母可以像数一样参与运算,为形成代数式的概念进行铺垫. 进一步理解字母表示数的意义,理解用代数式表示实际问题中数量关系的简洁性、必要性和一般性. 通过小结,使学生梳理本节课所学内容.
板书设计 代数式的意义 代数式: 用运算符号把数或表示数的字母连接起来的式子称为代数式. 单独的一个数或字母也是代数式. 2.列式的注意事项: (1)数与字母、字母和字母相乘省略乘号; (2)数与字母相乘时数字写在前面. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
第2课时 列代数式
课题 列代数式 课型 新授课
教学内容 教材第71-73页的内容
教学目标 1.会用代数式表示实际问题中的数量关系. 2.初步培养抽象能力、应用意识.
教学重难点 教学重点:熟练运用代数式表示实际问题中的数量关系. 教学难点:熟练运用代数式表示实际问题中的数量关系.
教 学 过 程 备 注
1.创设情境,引入课题 我们知道字母可以表示数,在解决问题时常需要把问题中与数量有关的词语用代数式表示出来,本节我们就来探究如何列代数式. 思考:如何用代数式表示a,b两数的和与差的积? 【师生活动】学生尝试解答,教师引导将问题分解成表示a,b两数的和,表示a,b两数的差,再表示它们的积三个问题,从而列出最终的代数式. 2.类比探究,学习新知 【问题1】列代数式:(1)一条河的水流速度为2.5 km/h,船在静水中的速度为v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度; (2)一个正方体的棱长是a,这个正方体的表面积是多少?体积呢? 【师生活动】学生先独立列式,然后同桌交流,学生代表板演展示,教师巡视指导. 解:(1)顺水行驶和逆水行驶时的速度分别是(v+2.5)km/h,(v-2.5)km/h; (2)面积=6a2,体积=a3. 归纳:(1)列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.分析实际问题时应注意:①抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;②理清语句层次,明确运算顺序;③联想相关概念和公式. (2)列式书写时应注意:①数与字母、字母与字母相乘省略乘号;②数与字母相乘时数字在前;③式子中出现除法运算时,一般按分数形式来写;④带分数与字母相乘时,把带分数化成假分数;⑤带单位时,适当加括号. 【问题2】上面的问题中,既有已知数,又有用字母表示的数,字母表示数有什么意义?用含有字母的代数式表示数量关系有什么意义? 【师生活动】学生尝试回答,教师根据学生回答情况进行评价. 归纳;用字母表示数,字母和数一样可以参与运算,可以用代数式把数量关系简明地表示出来. 3.学以致用,应用新知 【例】用代数式表示: 购买2个单价为a元的面包和3瓶单价为b元的饮料所需的钱数; 爸爸把a元钱存入银行,存期3年,年利率为2.75%,到期时的利息是多少元?; 某商品的进价为x元,先按进价的1.1倍标价,后又降价80元出售,现在的售价是多少元? 答案:(1)(2a+3b)元;(2)8.25%a元; (3)(1.1x-80)元. 4.随堂训练,巩固新知 1.用代数式表示: (1)比a的2倍大1的数; (2)a的相反数与b的一半的差; (3)a的平方除以b的商. 答案:(1)2a+1; (2)(-a)- b/2; (3)a2/b. 2.一列数1,4,7,10,13……按此规律排列,第n个数是 . 答案:3n-2 5.课堂小结,自我完善 (1)怎样列代数式? (2)列代数式时需要注意什么? (3)你还有什么疑惑? 6.布置作业 课本P73练习1-4. 利用分解问题降低难度的方式帮助学生分析问题、解决问题,为接下来的学习打下基础. 由浅入深,使学生透彻理解代数式的表示,培养学生的符号意识,培养他们应用新知识解决问题的能力. 进一步理解字母表示数的意义,理解用代数式表示实际问题中数量关系的简洁性、必要性和一般性. 例题的讲解,让学生巩固所学的新知识. 进一步巩固新知,及时检测学习效果. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 列代数式 1. 列简单的代数式 2. 根据实际问题列代数式 例 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
第3课时 反比例关系
课题 反比例关系 课型 新授课
教学内容 教材第73-75页的内容
教学目标 1.分析实际问题中两个量之间的变化,理解反比例关系,并用式子表示反比例关系. 2. 培养函数思想和数学建模能力,能用函数的观点分析、解决实际问题.
教学重难点 教学重点: 反比例关系及表示. 教学难点:从实际问题中抽象出数学问题,建立数学模型.
教 学 过 程 备 注
1.创设情境,引入课题 回顾本章引言中的问题(1).机器人t s能识别的范围是5t m2,也就是说机器人能识别的范围与所用时间的比例总是一定的(等于5).因此机器人能识别的范围与所用时间是成正比例的量,它们成正比例关系. 对于工程问题,如果工作量保持不变,工作时间与工作效率之间又有怎样的关系呢? 师生活动:由学生小组合作交流,教师肯定每一位学生说出的特点. 2.类比探究,学习新知 【问题1】北京是全球首个既举办过夏季奥运会又举办过冬季运动会的城市.在冬季奥运会前,某赛场计划造雪260 000 m3.解答下列问题: (1)根据每天造雪量,计算所需的造血天数,填写下表. 每天造雪量/m35 0005 2006 500...造雪天数...
(2)每天造雪量和造血天数这两个量是怎样变化的?它们之间有什么关系? 【师生活动】教师引导学生分析,此问题包含的三个量分别为造雪总量、每天造雪量和造雪天数,它们之间的关系为造雪总量=每天造雪量×造雪天数. 师生共同归纳:像这样,两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,这两个量就叫作成反比例的量,它们之间的关系叫作反比例关系. 【问题2】如何用式子表示反比例关系? 【师生活动】 师生共同总结:如果用字母x和y表示两个相关联的量,用k表示它们的积(k是一个确定的值,且k≠0),反比例关系可以用xy=k来表示. 3.学以致用,应用新知 【例】已知四个圆柱形容器内部的底面积分别为10cm2,20cm2,30cm2,60cm2.分别往这四个容器中注入300cm3的水. (1)四个容器中水的高度分别是多少厘米? (2)分别用x(单位:cm2)和y(单位:cm)表示容积内部的底面积与水的高度,用式子表示y与x的关系,y与x成什么比例关系? 答案: 4.随堂训练,巩固新知 1.汽车从甲地驶往乙地,汽车行驶的平均速度与时间是否成反比例关系?为什么? 答案:成反比例关系.路程一定,路程=速度×时间, 时间随速度的增大而减小. 2.长方体的体积一定,长方体的底面积与高是否成反比例关系?为什么? 答案:成反比例关系.体积一定,体积=底面积×高, 高随底面积的增大而减小. 3.某运输公司计划运输一批货物,每天运输的吨数与运输的天数之间的关系如下表: 每天运输的吨数50025010050...运输的天数12510...
(1)这批货物共有多少吨? (2)运输的天数是怎样随着每天运输的吨数的变化而变化的? (3)用t表示运输的天数,用a表示每天运输的吨数,用式子表示t与a的关系.t与a成什么比例关系? 答案:(1)这批货物共有500 吨; (2)运输的天数随着每天运输的吨数的减少而增加; (3)500=at,成反比例关系. 5.课堂小结,自我完善 (1)什么是反比例关系? (2)怎么用式子表示反比例关系? 6.布置作业 课本P75练习. 通过简单的复习正比例的相关概念,为探究、学习反比例的相关概念打下坚实的基础. 以问题串的形式创设情境,引起学生的认知冲突,使学生对新知识产生好奇,从而激发学生的学习兴趣和求知欲望. 结合实际,体会成反比例关系的两个量之间的依存关系,体会反比例关系在实际生活中的应用. 巩固反比例关系的概念,使学生体会到数学来源于生活,应用于生活的价值美. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 反比例关系 1.反比例关系 2.表示:xy=k(k是一个确定的值,且k≠0) 例 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
3.2 代数式的值
第1课时 求代数式的值
课题 求代数式的值 课型 新授课
教学内容 教材第79-80页的内容
教学目标 1.会求代数式的值. 2.培养运算能力及分析问题、解决问题的能力.
教学重难点 教学重点: 在解决具体问题时,熟练求出代数式的值. 教学难点: 在解决具体问题时,熟练求出代数式的值.
教 学 过 程 备 注
1.创设情境,引入课题 为了开展体育活动,学校要购置一批排球,每班配5个,学校另外留20个.学校总共需要购置多少个排球? 【师生活动】学生尝试解答,记全校的班级数是n,需要购置的排球总数是 5n+20. 2.类比探究,学习新知 【问题1】上述问题中,如果班级数是15,那么需要购置多少个排球? 如果班级数是20呢? 【师生活动】学生尝试解答.如果班级数是15,用15代替字母n,那么需要购置的排球总数是5n+20=5×15+20=95;如果班级数是20,用20代替字母n,那么需要购置的排球总数是5n+20=5×20+20=120. 总结:一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同. 3.学以致用,应用新知 【例1】根据下列x,y的值,分别求代数式2x+3y的值: (1)x=15,y=12;(2)x=1,y=. 答案:(1)当x=15时,y=12时, 2x+3y=2×15+3×12=66; (2)当x=1,y=时,2x+3y=2×1+3×=. 【例2】根据下列a,b的值,分别求代数式a2 的值; (1)a=4,b=12;(2)a=-3,b=2. 答案:(1)当a=4,b=12时,a2 =42-=13; (2)当a=-3,b=2时,a2 =(-3)2- = . 【例3】冰糖葫芦是我国传统小吃,若有a个山楂,按每串冰糖葫芦的山楂个数相等的规定,穿了b串冰糖葫芦,还剩余c个山楂,则每串冰糖葫芦的山楂个数是多少?当a=150,b=18,c=6时,求每串冰糖葫芦的山楂个数. 解:每串冰糖葫芦的山楂个数是. 当a=150,b=18,c=6时,. 即每串冰糖葫芦的山楂个数是8. 4.随堂训练,巩固新知 1.当x=﹣1时,则代数式x+4的值为( ) A.5 B.﹣3 C.3 D.﹣5 答案:C 2.已知m=﹣2,n=1,则代数式n﹣m的值为( ) A.2 B.﹣2 C.﹣3 D.3 答案:D 3. 已知代数式2a2b+3ab﹣4,当a=﹣3,b=﹣2时,求m的值. 答案:当a=﹣3,b=﹣2时,2a2b+3ab﹣4 =2×(﹣3)2×(﹣2)+3×(﹣3)×(﹣2)﹣4 =2×9×(﹣2)+3×(﹣3)×(﹣2)﹣4 =﹣36+18﹣4 =﹣22. 4. 当x=2,y=-3时,求代数式x2+2xy+y2的值. 答案:当x=2,y=-3时, x2+2xy+y2=22+2×2×( 3)+( 3)2=1. 5.课堂小结,自我完善 (1)如何求代数式的值? (2)求代数式的值时,需要注意什么? 6.布置作业 课本P80练习1-3,P82习题3.2第1,3,4题. 引入实际问题,使学生感受到学习代数式的值的运算是实际需要.此环节教师应关注学生是否能正确列式,得出正确的式子. 通过让学生解决生活中的实际问题,进一步理解代数式的值,培养计算能力,激发学习兴趣. 让学生进一步了解代数式的值的意义,提高学生的数学运算能力. 通过练习加深对本节课内容的理解. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 求代数式的值 一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
第2课时 列代数式求值
课题 列代数式求值 课型 新授课
教学内容 教材第80-81页的内容
教学目标 1.熟练掌握几何图形公式,根据实际问题列代数式并求值. 2.通过现实问题情境进一步理解用字母表示数的意义.
教学重难点 教学重点:根据实际问题列代数式求值. 教学难点:根据实际问题列代数式求值.
教 学 过 程 备 注
1.创设情境,引入课题 有些同类事物中的数量关系常常可以用公式来描还,例如,在行程问题中,用s表示路程,v表示速度,t表示时间,就可以得到路程公式s=vt,它表示了路程、速度、时间这三个量之间的关系.知道v,t的值,就可以利用公式求出s的值.在小学,我们学习过许多公式,如长方形、正方形、三角形、梯形、圆等图形的面积公式,长方体、正方体等图形的体积公式,等等.在解决有关问题时,经常用这些公式进行计算. 2.类比探究,学习新知 【问题1】某学校操场最内测的跑道由两段直道和两端半圆形的弯道组成,其中直道的长为a,半圆形弯道的直径为b. (1)用代数式表示这条跑道的周长; (2)当a=67.3 m,b=52.6 m时,求这条跑道的周长(π取3.14,结果取整数). 【师生活动】学生尝试解答.(1)两条直道的长度为2a,两端半圆形弯道可以看成一个圆,其周长为πb,所以跑道的周长为2a+πb. (2)当a=67.3 m,b=52.6 m时, 2a+πb=2×67.3+3.14×52.6≈300(m). 因此,这条跑道的周长约为300 m. 教师强调:本题中用到了圆的周长公式,对于长方形、正方形、三角形、圆等的周长、面积公式要熟练掌握.根据实际问题列出代数式,再用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果. 3.学以致用,应用新知 【例】如图,公园有一个“T”型空地(即阴影部分,单位:米). (1)用含x,y的代数式表示空地的面积;(结果要进行化简) (2)公园管理部门计划对空地铺设草坪.已知每平方米草坪的费用为200元,若x,y满足(x﹣3)2+|y﹣5|=0,求铺设草坪的总费用. 解:(1)2x(2x+2y)+2xy =(4x2+6xy)m2. (2)由(x﹣3)2+|y﹣5|=0,可得x=3,y=5. 将x=3,y=5代入4x2+6xy,得 原式=4×32+6×3×5=126(m2). 所以铺设草坪的总费用是:126×200=25200元. 4.随堂训练,巩固新知 1.一个长方体纸箱的长是a,宽与高都是b,这个纸箱的体积V是多少?如果a=60 cm,b=40 cm,求V的值. 答案:V=ab2,当a=60 cm,b=40 cm时,V=96 000 cm3. 2. 如图长方形的长为a,宽为2b, (1)用含a、b的式子表示图中阴影部分的面积S. (2)当a=5cm,b=2cm时,求阴影部分面积S的值.(其中π取3.14) 答案:解:(1)∵长方形的长为a,宽为2b, ∴S阴影=2ab﹣πb2; (2)a=5cm,b=2cm时, S阴影=20﹣3.14×4=7.44(cm2), 即S阴影=7.44(cm2). 3. 如图,学校操场主席台前计划修建一块凹字形花坛.(单位:米) (1)用含a,b的整式表示花坛的面积; (2)若a=4,b=3,工程费为500元/平方米,求建花坛的总工程费为多少元? 答案:(1)(a+3b+a)(2a+b)﹣2a 3b =4a2+8ab+3b2﹣6ab =(4a2+2ab+3b2)m2. 答:花坛的面积是(4a2+2ab+3b2)m2. (2)当a=4,b=3时, 4a2+2ab+3b2 =4×42+4×2×3+3×32 =115(m2), 115×500=57500(元). 答:建花坛的总工程费为57500元. 5.课堂小结,自我完善 (1)本节你学到了什么?试着总结一下. (2)除了今天学习的公式,还有哪些公式可以用来描述实际问题中的数量关系? 6.布置作业 课本P81练习1-3,P82习题3.2第6题. 引导学生回忆学过的几何公式,感受到代数式与几何公式和实际生活的密切联系.此环节教师应关注学生是否能正确列式,得出正确的式子. 鼓励学生自主探索,体会用公式解决数学问题的方法. 通过让学生解决生活中的实际问题,进一步理解代数式的值,培养计算能力,激发学习兴趣. 通过练习加深对本节内容的理解,使学生感受“数式通性”及用公式描述数量关系的抽象过程. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 列代数式求值 常用的数学公式 例 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
21世纪教育网(www.21cnjy.com)
同课章节目录
