人教版七年级数学上册 第四章 整式的加减 全章教案
文档属性
| 名称 | 人教版七年级数学上册 第四章 整式的加减 全章教案 | 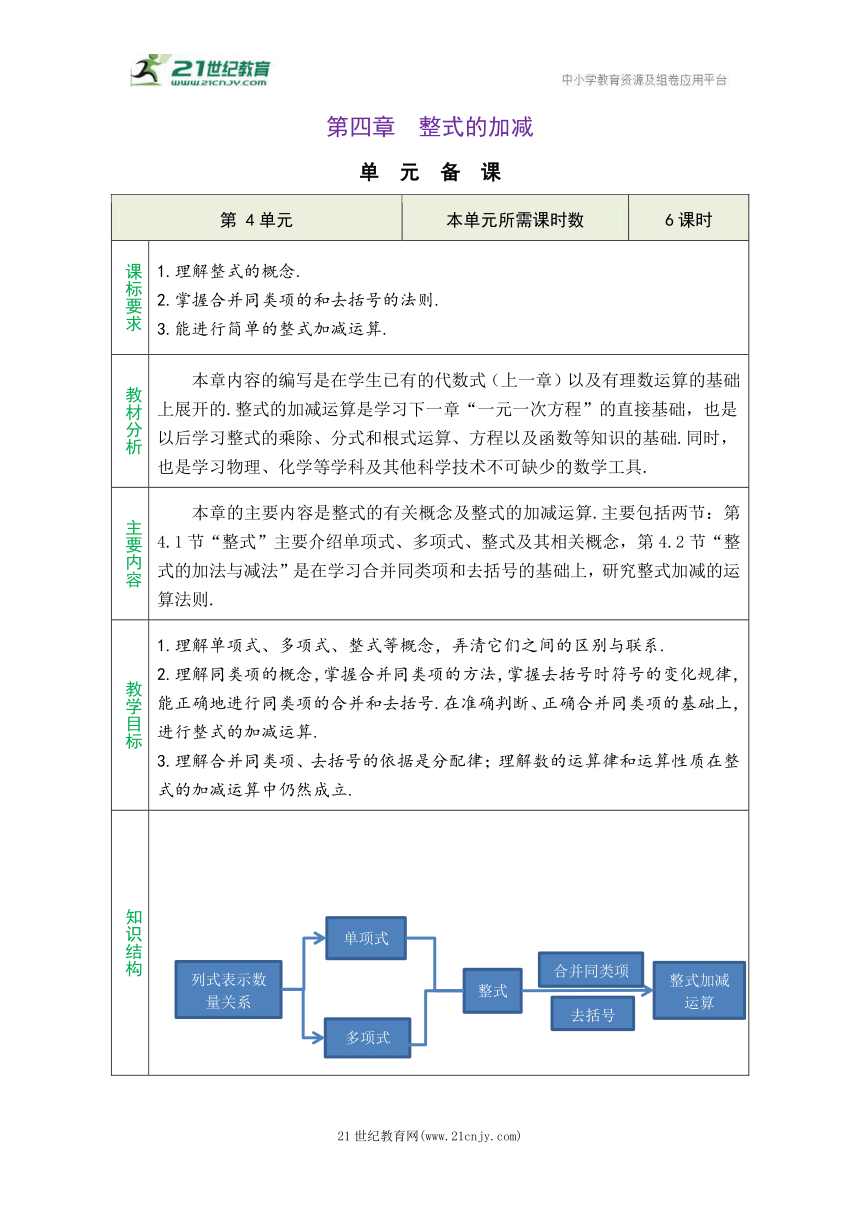 | |
| 格式 | docx | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 05:29:44 | ||
图片预览




文档简介
第四章 整式的加减
单 元 备 课
第 4单元 本单元所需课时数 6课时
课标要求 1.理解整式的概念. 2.掌握合并同类项的和去括号的法则. 3.能进行简单的整式加减运算.
教材分析 本章内容的编写是在学生已有的代数式(上一章)以及有理数运算的基础上展开的.整式的加减运算是学习下一章“一元一次方程”的直接基础,也是以后学习整式的乘除、分式和根式运算、方程以及函数等知识的基础.同时,也是学习物理、化学等学科及其他科学技术不可缺少的数学工具.
主要内容 本章的主要内容是整式的有关概念及整式的加减运算.主要包括两节:第4.1节“整式”主要介绍单项式、多项式、整式及其相关概念,第4.2节“整式的加法与减法”是在学习合并同类项和去括号的基础上,研究整式加减的运算法则.
教学目标 1.理解单项式、多项式、整式等概念,弄清它们之间的区别与联系. 2.理解同类项的概念,掌握合并同类项的方法,掌握去括号时符号的变化规律,能正确地进行同类项的合并和去括号.在准确判断、正确合并同类项的基础上,进行整式的加减运算. 3.理解合并同类项、去括号的依据是分配律;理解数的运算律和运算性质在整式的加减运算中仍然成立.
知识结构
课时分配 4.1 整 式 2课时 4.2 整式的加法与减法 3课时 教学活动 小结 1课时
教与学建议 1.加强式与数的类比教学. 2.抓住重点、加强练习,打好基础.
4.1 整式
第1课时
课题 单项式 课型 新授课
教学内容 教材第89-91页的内容
教学目标 1.理解单项式的概念,掌握单项式的系数和次数的概念,能判断一个代数式是不是单项式,对于一个单项式能说出它的系数和次数. 2.再进一步理解用字母表示数量关系的过程中建立符号意识,激发学生学习数学的积极性.
教学重难点 教学重点:单项式、单项式的系数和次数的概念. 教学难点:用字母表示数量关系及理解与单项式有关的概念.
教学活动
教学过程 备 注
1.创设情境,引入课题 【问题1】我们来看引言和上一章中遇到过的一些代数式 92t,a2,0.9p,a2h, 这些代数式有什么共同特点? 【师生活动】学生尝试解答,教师总结归纳. 2.类比探究,学习新知 【探究1】单项式的相关概念 【问题2】单项式的判断: 判断下列各式是否是单项式,是的打“√”,不是的打“×”,并说明理由. (1)m;(2)-9;(3)-2xy;(4)x+1;(5)2a-b; (6);(7);(8)9πx2;(9);(10). 【师生活动】学生尝试解答,教师总结单项式的概念. 总结:数或字母的积组成的式子叫作单项式,单独的一个数或一个字母也是单项式. 【问题3】确定单项式的系数和次数: 单项式4x6a2a3-nvt2πRx2yz次数
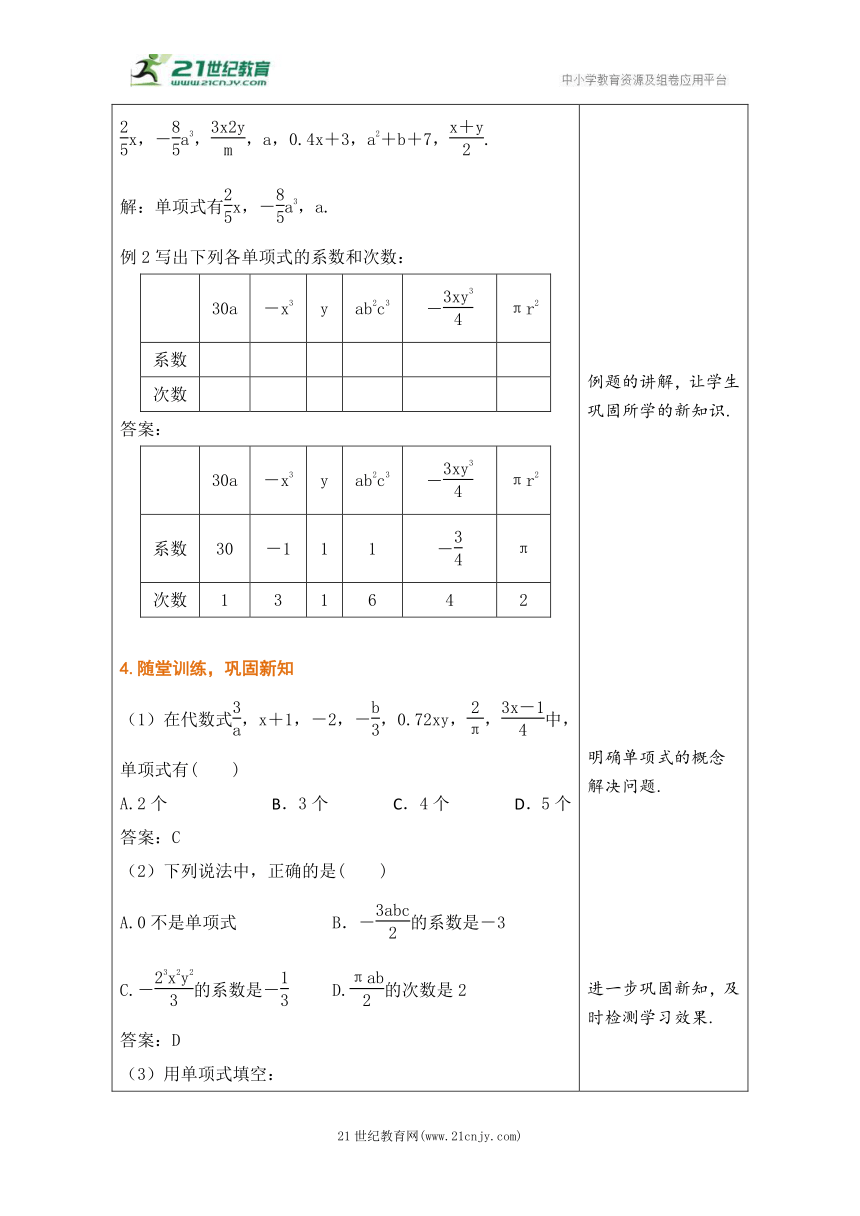
【师生活动】先由学生归纳总结,再由教师补充纠错. 总结:(1)一个单项式中,所有字母的指数的和叫作这个单项式的次数. (2)单项式次数只与字母指数有关(π是常数). 【探究2】单项式的应用 【问题4】用单项式填空,并指出它们的系数和次数. 1每包书有12册,n包书有 册. 2.底边长为a,高为h的三角形的面积是 . 3.一个长方体的长和宽都是a,高为h,它的体积是 . 4.一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为 . 5.一个长方形的长为0.9,宽为a,面积是 . 【问题5】用字母表示数后,同一个代数式在不同的问题中可以表示不同的含义.例如,在问题4,5中,所填的结果都是0.9a,一个是表示电视机的售价,一个表示长方形的面积,你还能赋予0.9a一个含义吗?(学生回答) 【师生活动】先由学生归纳总结,再由教师补充纠错. 3.学以致用,应用新知 例1下列各式中,哪些是单项式? x,-a3,,a,0.4x+3,a2+b+7,. 解:单项式有x,-a3,a. 例2写出下列各单项式的系数和次数: 30a-x3yab2c3-πr2系数次数
答案: 30a-x3yab2c3-πr2系数30-111-π次数131642
4.随堂训练,巩固新知 (1)在代数式,x+1,-2,-,0.72xy,,中,单项式有( ) A.2个 B.3个 C.4个 D.5个 答案:C (2)下列说法中,正确的是( ) A.0不是单项式 B.-的系数是-3 C.-的系数是- D.的次数是2 答案:D (3)用单项式填空: ①一辆汽车的速度是v千米/时,行驶t小时所走过的路程为_____千米; ②王洁同学买2本练习本花了n元,那么买m本练习本要_____元; ③边长为a的正方体的表面积为_____,正方体的体积为_____. 答案:①vt;②;③6a2;a3. 5.课堂小结,自我完善 教师与学生一起回顾本节课所学主要内容,并请学生回答以下问题:
(1)本节课学习了哪些主要内容? (2)判断单项式的系数和次数需要注意什么?
(3)你还有什么疑惑? 6.布置作业 课本P91练习1-2. 培养学生观察、发现的能力,总结出单项式的概念. 由浅入深,使学生透彻理解单项式的有关概念,培养他们应用新知识解决问题的能力. 熟知三角形,长方形面积公式. 例题的讲解,让学生巩固所学的新知识. 明确单项式的概念解决问题. 进一步巩固新知,及时检测学习效果. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 单项式 1.单项式的概念:数或字母的积 2.单项式的系数:数字因数 3.单项式的次数:所有字母的指数和 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.1 整式
第2课时
课题 多项式及整式 课型 新授课
教学内容 教材第91-93页的内容
教学目标 1.通过本节课的学习,学生掌握整式、多项式的项及其次数、常数项的概念. 2.知道整式和单项式、多项式的关系. 3.由单项式与多项式归纳出整式,这样更有利于学生把握概念的内涵与外延,有利于学生知识的迁移和知识结构体系的更新.
教学重难点 教学重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数,以及常数项等概念. 教学难点:多项式的次数.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 【问题1】你能指出下面哪些式子是单项式吗?并指出单项式的系数与次数. 3,π,a2b,,a2+b2,2+b. 【师生活动】由学生思考好后举手回答,锻炼他们的口答能力.单项式π的系数与次数比较容易错,教师适当解析. 【问题2】观察v+2.5,v-2.5,3x+5y+2z,ab-πr2,x2+2x+18,这些式子有什么特点? 【师生活动】由学生小组合作交流,教师肯定每一位学生说出的特点.如果学生仍然有困难,教师给予提示: (1)上面的式子是单项式吗? (2)这些式子与单项式有联系吗? 2.类比探究,学习新知 【问题3】什么叫多项式? 【师生活动】几个单项式的和叫作多项式. 【问题4】什么叫多项式的项和次数?多项式x2+2x+18是几次几项式? 【师生活动】在多项式中,每个单项式叫作多项式的项.不含字母的项叫作常数项.一个多项式含有几项,就叫几项式. 多项式里,次数最高的项的次数,叫作这个多项式的次数. x2+2x+18是二次三项式. 【问题5】下列多项式的项和次数分别是什么? v+2.5,3x+5y+2z,ab-πr2. 【师生活动】v+2.5的项分别是v,2.5,次数是1;3x+5y+2z的项分别是3x,5y,2z,次数是1;ab-πr2的项分别是ab,-πr2,次数是2. 【问题6】你认为确定多项式的项、次数时应注意什么? 【师生活动】①多项式的项应包括该项的符号;②多项式的次数为最高次项的次数;③常数项是多项式中的特殊项,确定多项式项数时不要漏掉. 【问题7】什么叫整式?下列式子哪些是整式? ①-x;②x+1;③π;④-3;⑤-+25. 【师生活动】出示自学提纲,让学生按要求自学教科书内容,独立解决相关问题.教师进行巡视,关注对于概念理解还不太透彻的学生;板书多项式、整式有关概念,强调:(1)多项式的项应包括该项的符号;(2)多项式的次数为最高次项的次数;(3)常数项是多项式中的特殊项,确定多项式项数时不要漏掉. 3.学以致用,应用新知 例1 下列式子中,哪些是整式?哪些是单项式?哪些是多项式? a,ax2+bx+c,-5,π,,. 解:单项式:a,-5,π. 多项式:ax2+bx+c,. 整式:a,ax2+bx+c,-5,π,. 例2 指出下列多项式的次数与项: (1)xy-; (2)a2+2a2b+ab2-b2; (3)2m3n3-3m2n2+mn. 解:(1)次数:2,项:xy,-. (2)次数:3,项:a2,2a2b,ab2,-b2. (3)次数:6,项:2m3n3,-3m2n2,mn. 例3 若多项式-x2y2n+1z+x2y+4是八次三项式,则n=_______. 答案:2 例4 如图,用式子表示圆环的面积,当R=15 cm,r=10 cm时,求圆环的面积(π取3.14). 解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是πR2-πr2. 当R=15 cm,r=10 cm时,圆环的面积是 πR2-πr2=3.14×152-3.14×102=392.5(cm2). 答:这个圆环的面积是392.5 cm2. 4.随堂训练,巩固新知 (1)把下列各式的序号填在相应的集合里. ①0;②x2;③-x2-2x+5;④;⑤xy;⑥8+;⑦-5;⑧. 整式:{ ,…} 多项式:{ ,…} 单项式:{ ,…} 答案:整式:{①②③④⑤⑥⑦⑧,…} 多项式:{③⑥⑧,…} 单项式:{①②④⑤⑦,…} (2)指出下列多项式的项和次数. ①a3-a2b+ab2-b3;②3n4-2n2+1. 答案:①项:a3,-a2b,ab2,-b3,次数:3. ②项:3n4,-2n2,1,次数:4. (3)指出下列多项式是几次几项式: ①x3-x+1; ②x3-2x2y2+3y2. 答案:①三次三项式.②四次三项式. (4)a,b分别表示梯形的上底和下底,h表示梯形的高,则梯形的面积S=__________,当a=2 cm,b=4 cm,h=5 cm时,S=_________cm2. 答案:(a+b)h;15 5.课堂小结,自我完善 (1)多项式的定义: 几个单项式的和叫作多项式. (2)多项式的项和次数的定义: 在多项式中,每个单项式叫作多项式的项.不含字母的项叫作常数项. 多项式里,次数最高项的次数,就是这个多项式的次数. (3)注意:①多项式的项是应包括该项的符号;②多项式的次数为最高次项的次数;③常数项是多项式中的特殊项,确定多项式项数时不要漏掉. (4)整式的定义: 单项式与多项式统称整式. 6.布置作业 课本P93练习1-3. 通过简单的复习单项式的相关概念,为探究、学习多项式的相关概念打下坚实的基础. 以问题串的形式创设情境,引起学生的认知冲突,使学生对新知识产生好奇,从而激发学生的学习兴趣和求知欲望. 由浅入深,使学生对多项式的有关概念的理解更加透彻,培养他们应用新知识解决问题的能力. 1.了解单项式、多项式、整式的相关概念,会判断单项式、整式、多项式. 2.会判断多项式的次数和项数. 3.巩固多项式的概念,同时为学生创造用多项式表示实际问题中的数量关系的机会,培养学生的列式能力,同时使学生体会到数学来源于生活,应用于生活的价值美. 考查整式的分类. 熟知并理解多项式的项和次数的概念. 会判断多项式项数与次数. 用多项式表示数量关系. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 多项式及整式 1.多项式的定义:几个单项式的和叫作多项式. 2.多项式的项和次数的定义: 在多项式中,每个单项式叫作多项式的项.不含字母的项叫作常数项. 多项式里,次数最高的项的次数,叫作这个多项式的次数. 3.整式的定义: 单项式与多项式统称整式. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.2 整式的加法与减法
第1课时
课题 合并同类项 课型 新授课
教学内容 教材第95-98页的内容
教学目标 1.了解同类项及合并同类项的概念. 2.通过类比数的运算探究合并同类项的法则,从中体会“数式通性”和类比的思想,培养学生观察、探索、分类、归纳的能力.
教学重难点 教学重点:理解同类项的概念及合并同类项法则. 教学难点:正确判断同类项,准确合并同类项.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 【问题1】汽车从香港口岸到西人工岛包含两段路程,一段为香港口岸到东人工岛,另一段为海底隧道.如果汽车通过海底隧道需要a h,那么从香港口岸到东人工岛所需时间是1.25a h,香港口岸到西人工岛的全长(单位:km)是多少呢? 【师生活动】学生尝试解答,得到香港口岸到西人工岛的全长为72a+96×1.25a=72a+120a. 教师追问:这个式子还能化简吗? 2.类比探究,学习新知 类比数的运算,我们应如何化简式子72a+120a? 【问题2】(1)运用运算律计算: 72×2+120×2= , 72×(-2)+120×(-2)= ; (2)根据(1)中的方法完成下面的运算: 72a+120a = . 【师生活动】根据分配律,可得72×2+120×2=(72+120)×2=192×2=384; 72×(-2)+120×(-2)=(72+120)×(-2)=-384. 教师提问:式子72a+120a与(1)中的两个算式有什么联系? 根据学生的回答情况引导归纳:算式72×2+120×2与72×(-2)+120×(-2)和式子72a+120a具有相同的结构,并且字母t代表的是一个因(乘)数,因此根据分配律应有72a+120a=(72+120)a=192a. 【问题3】类比式子72a+120a的化简方法,填空: (1)72a-120a=( )a; (2)3m2+2m2=( )m2; (3)3xy2-4xy2=( )xy2. 【师生活动】利用分配律可得: 72a-120a=(72-120)a=-48a,3m2+2m2=(3+2)m2=5m2, 3xy2-4xy2=(3-4)xy2=-xy2. 在计算72a-120a时,注意分配律的使用:72a-120a=[72+(-120)]a=(72-120)a. 【问题4】(1)观察多项式72a+120a,72a-120a,3m2+2m2,3xy2-4xy2,各多项式的项有什么共同特点? (2)通过以上化简计算,你能从中得出什么规律? 【师生活动】每个式子的项含有相同的字母;相同字母的指数也相同.根据分配律把多项式各项的系数相加,字母部分保持不变. 在讨论交流的基础上,教师引导学生归纳同类项的定义、合并同类项的定义和法则. 像72a与-120a,3m2与2m2,3xy2与4xy2这样,所含字母相同,并且相同字母的指数也相同的项叫作同类项.几个常数项也是同类项. 把多项式中的同类项合并成一项,叫作合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的和,字母连同它的指数不变. 【问题5】找出多项式4x2+2x+7+3x-8x2-2中的同类项,并进行合并,由此归纳出化简多项式的一般步骤. 【师生活动】教师引导学生口述,教师给出板书演示. 4x2+2x+7+3x-8x2-2 =4x2-8x2+2x+3x+7-2 (交换律) =(4x2-8x2)+(2x+3x)+(7-2) (结合律) =(4-8)x2+(2+3)x+(7-2) (分配律) =-4 x2+5x+5. 找出同类项并做不同的标记,运用交换律、结合律分配律把同类项结合并合并,最后按某个字母的降幂或升幂排列. 3.学以致用,应用新知 【例1】下列各组单项式,是同类项的是( ) A.2ab2与a2b B.-x与y C.3与3a D.-x3y2与-3x3y2 答案:D 【变式】已知单项式3xmy3与-4x5y3是同类项,则m= . 答案:5 【例2】合并下列各式的同类项: (1)xy2-xy2; (2)-3x2y+2x2y+3x2y-2x2y; (3)4a2+3b2+2ab-4a2-4b2. 答案:(1)xy2-xy2=xy2;(2)-3x2y+2x2y+3x2y-2x2y=- x2y+ xy2;(3)4a2+3b2+2ab-4a2-4b2=- b2+2ab. 【例3】求多项式2x2-5x+x2+4x-3x2-2的值,其中x=. 答案:- 【变式】求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3。 答案:1 【例4】(1)水库水位第一天连续下降了a h,每小时平均下降2cm;第二天连续上升了a h,每小时平均上升0.5cm,这两天水位总的变化情况如何? (2)某商店原有5袋大米,每袋大米为x kg.上午售出3袋,下午又购进同样包装的大米4袋.进货后这个商店有大米多少千克? 答案:(1)-2a+0.5a=-1.5a.(2)5x-3x+4x=6x. 4.随堂训练,巩固新知 (1)下列单项式中,与a3b2是同类项的是( ) A.- a2b3 B.2a3b2 C.- ab4 D. a4b 答案:B (2)下列运算正确的是( ) A.3a+2a=5 B.3a-2a=1 C. 3a-2a=a D. 3a-2a=6a 答案:C (3)化简:①-2ab+6ab-(-8ab);②4xy-3x2-3xy+2x2。 答案:①12ab;②xy- x2. (4)求下列各式的值: ①4a2+2a+1-3a2-3a,其中a=-1;②4xy-3x2-3xy-2y+3x2,其中x=-1,y=-3. 答案:①3;②9. (5)已知2xmy与3x2yn-1的和是单项式,求m,n的值. 答案:m=2,n=2. 5.课堂小结,自我完善 (1)判断同类项的两条标准:所含字母相同;相同字母的指数也相同 (2)合并同类项后,所得项的系数是合并前各同类项的系数的和,字母连同它的部分不变. (3)多项式中合并同类项的步骤:①找出同类项做出标记;②运用交换律、结合律将多项式的同类项结合;③运用分配律合并同类项;④按同一个字母的降幂(或升幂)排列. 6.布置作业 课本P98练习1-3,P102习题4.2第1题. 引入实际问题,使学生感受到学习含有字母的式子的运算是实际需要.此环节教师应关注学生是否能正确列式,得出正确的式子,从而引出对合并同类项法则的探讨. 通过用分配律进行有理数的运算,帮助理解用分配律化简式子72a+120a的方法,为进一步类比学习整式的运算提供方法上的借鉴.通过引导学生观察比较,发现三个算式的联系,体会由“数”到“式”是由特殊到一般的思想方法,初步感受“数式通性”和类比的数学思想. 教师应关注学生是否正确区分运算符号和性质符号.通过几组不同形式的同类项,感受不同类型式子的组成,突出同类项的特点,为归纳同类项的概念和合并同类项法则做好铺垫. 在观察、比较中,发现各多项式的共同特征,分析运算特点,归纳出同类项、合并同类项及合并同类项的法则. 归纳化简多项式的一般步骤,规范学生的解题过程,避免出现漏项等易错点,帮助学生快速掌握化简多项式的方法. 加深学生对同类项的概念和合并同类项法则的理解和运用,提高运算能力. 在求多项式的值时,先化简再代入求值往往可以简化计算. 通过让学生解决生活中的实际问题,进一步理解合并同类项的概念及法则,培养计算能力,激发学习兴趣. 正确理解同类项的概念. 掌握合并同类项法则. 两个单项式的和还是单项式等同于这两个单项式是同类项. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 合并同类项 概念 同类项 举例 概念 合并同类项 法则 应用 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.2 整式的加法与减法
第2课时
课题 去括号 课型 新授课
教学内容 教材第98-100页的内容
教学目标 1.学生经过观察、合作交流、讨论总结出去括号的法则,并掌握. 2.能正确且较为熟练地运用去括号法则化简代数式. 3.经历带有括号的有理数的运算,发现去括号时符号变化的规律,归纳出去括号法则,培养学生观察、分析、归纳能力,发展学生的数学思维.
教学重难点 教学重点:准确应用去括号法则将整式化简. 教学难点:准确应用去括号法则将整式化简.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 用火柴棒搭正方形时,怎样计算所需要的火柴棒的根数吗?拿出准备好的火柴棒,自己搭一下,然后再按如下做法搭. 小明的做法: 第一个正方形用4根火柴棒,每增加一个正方形增加3根火柴棒,那么搭x个正方形就需要火柴棒[4+3(x-1)]根. 小颖的做法: 每一个正方形可以看成是用4根火柴棒搭成的,然后再减去多算的根数,就得到搭x个正方形需要的火柴棒根数是4x-(x-1). 小刚的做法: 第一个正方形可以看成是用3根火柴增加1根火柴棒搭成的,此后每增加一个正方形就增加3根火柴棒,那么搭x个正方形共需(3x+1)根火柴棒. 他们的做法都正确吗?你能解释吗? 2.类比探究,学习新知 【探究】去括号法则 本章引言中的问题(3). 汽车通过主桥的行驶时间是b h,那么汽车在主桥上行驶的路程是92b km;通过海底隧道所需时间比通过主桥的时间少0.15 h,那么汽车在海底隧道行驶的时间是(b-0.15)h,行驶的路程是72(b-0.15)km.因此,主桥与海底隧道长度的和(单位:km)为92b+72(b-0.15), 主桥与海底隧道长度的差(单位:km)为92b-72(b-0.15). 观察上面的两个式子,你们知道该怎样化简吗 【师生活动】教师指导学生解答问题,师生共同讨论、交流,最后由老师归纳总结出去括号的方法. 一般地,一个数与一个多项式相乘,需要去括号,去括号就是用括号外的数乘括号内的每一项,再把所得的积相加. 注意:(1)去括号时改变了代数式的形式,但不改变代数式的值; (2)去括号时用括号外的数乘括号内的每一项,不要漏乘. 3.学以致用,应用新知 例1 化简下列各式: (1)x-(3x-2)+(2x+3); (2)(3a2+a-5)-(4-a+7a2); (3)(2m-3)+m-(3m-2); (4)3(4x-2y)-3(-y+8x). 答案:(1)5.(2)-4a2+2a-9.(3)-1.(4)-12x-3y. 例2 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是 a km/h. (1)2 h后两船相距多远? (2)2 h后甲船比乙船多航行多少千米? 解:顺水航速=船速+水速=(50+a) km/h, 逆水航速=船速-水速=(50-a) km/h. (1)2 h后两船相距(单位:km) 2(50+a)+2(50-a)=100+2a+100-2a=200. (2)2 h后甲船比乙船多航行(单位:km) 2(50+a)-2(50-a)=100+2a-100+2a=4a. 4.随堂训练,巩固新知 (1)-(x-2y+3z)去括号后的结果为( ) A.x-2y+3z B.-x+2y-3z C.x+2y-3z D.-x+2y+3z 答案:B (2)下列各式中,去括号正确的是( ) A.x2-(x-y+2z)=x2-x+y+2z B.x-(-2x+3y-1)=x+2x+3y+1 C.3x+2(x-2y+1)=3x-2x-2y-2 D.-(x-2)-2(x2+2)=-x+2-2x2-4 答案:D (3)化简: ①5a-(2a-4b); ②2x2+3(2x-x2); ③6a2-4ab-4(2a2+ab);④-3(2x2-xy)+4(x2+xy-6). 解:①原式=3a+4b.②原式=-x2+6x. ③原式=-2a2-6ab.④原式=-2x2+7xy-24. (4)先化简,再求值:(4a2-3a)-(2a2+a-1)+(2-a2)+4a,其中a=-2. 解:原式=a2+3.当a=-2时,原式=(-2)2+3=7. 5.课堂小结,自我完善 教师与学生一起回顾本节课所学主要内容,并请学生回答以下问题:
(1)本节课学习了哪些主要内容? (2)去括号时需要注意什么?
(3)你还有什么疑惑? 6.布置作业 课本P100练习1-4,P102习题4.2第2-4题. 让学生经历动手实践,将实际问题抽象为数学问题的过程,感受数学知识与生活的联系,激发学生的学习兴趣,也为新课的学习做好铺垫. 深入思考,培养学生逆向思维的习惯,从而更进一步加深学生对去括号法则的理解. 可以让学生先独立尝试解决,然后通过学生反馈的情况,教师针对一些存在的问题进行示范性讲解并板书. 运用所归纳的知识解决问题,提高学生解决问题的能力. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 去括号法则 一般地,一个数与一个多项式相乘,需要去括号,去括号就是用括号外的数乘括号内的每一项,再把所得的积相加. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.2 整式的加法与减法
第3课时
课题 整式的加减 课型 新授课
教学内容 教材第100-101页的内容
教学目标 1.能根据题意列出式子,会用整式加减的运算法则进行整式加减运算,并能说明其中的算理. 2.经历用字母表示实际问题中的数量关系的过程,发展符号感,提高运算能力及综合运用知识进行分析、解决问题的能力,发展数学思维.
教学重难点 教学重点:列式表示实际问题中的数量关系,会用整式加减的运算法则进行整式加减运算. 教学难点:列式表示问题中的数量关系,整式加减的运算法则的运用.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 小明乘公共汽车到城里的书店买书,小明上车时,发现车上已有(3a-b)人,车到中途站时,有(2a-3)人下车,但又上来若干人,这时公共汽车上共有(8a-5b)人,则中途有多少人上车? 你能用学到的数学知识解决这个实际问题吗? 现在我们一起来分析一下: 要计算中途上车的人数,可用总人数减去下车后剩下的人数,因为原来有(3a-b)人,加上小明,所以没人下车之前,车上共有(3a-b+1)人,下去(2a-3)人后,车里还有(3a-b+1)-(2a-3)=(a-b+4)人,用总人数(8a-5b)减去(a-b+4)即可求出上车的人数. 这就是我们今天要学习的整式的加减.如何进行整式的加减呢? 【师生活动】师生一起分析完,让学生自己列出式子(8a-5b)-[(3a-b+1)-(2a-3)]表示中途上车的人数.如果学生列出式子有困难的话,教师要给予一定的提示或者师生共同列出式子. 2.类比探究,学习新知 【问题1】做大小两个长方体纸盒,尺寸如下(单位:cm): 长宽高小纸盒abc大纸盒1.5a2b2c
(1)做这两个纸盒共用纸多少平方厘米? (2)做大纸盒比做小纸盒多用纸多少平方厘米? 【问题2】求x-2(x-y2)+(-x+y2)的值,其中x= -2,y=. 【问题3】化简: (1)(x+y)-(2x-3y); (2)2(a2-2b2)-3(2a2+b2). 以上化简实际上进行了哪些运算? 【师生活动】教师指导学生解答问题,师生共同讨论、交流,最后由教师归纳总结出整式加减的运算法则: 几个整式相加减,如果有括号就先去括号,然后再合并同类项. 【问题4】笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2 支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱? 答案:小红和小明买笔记本共花费(3x+4x)元,圆珠笔共花费(2y+3y)元. 小红和小明一共花费(单位:元) (3x+4x) + (2y+3y) = 7x+5y. 【师生活动】教师指导学生解答问题,师生共同讨论、交流,最后由教师归纳总结出整式加减解决实际问题的一般步骤. (1) 根据题意列代数式; (2) 去括号、合并同类项; (3) 得出最后结果. 3.学以致用,应用新知 【例1】(1)3a+2-(-4a); (2)(ab-3a2)-2b2-5ab-(a2-2ab); 解:(1)原式=7a+2.(2)原式=-4a2-2b2-2ab. 【例2】先化简再求值: ,其中. 解:(1)﹣(9x3﹣4x2+5)﹣(﹣3﹣8x3+3x2) =﹣9x3+4x2﹣5+3+8x3﹣3x2 =﹣x3+x2﹣2 当x=2时,原式=﹣23+22﹣2=﹣6 4.随堂训练,巩固新知 (1)①2(x2+3)-(5-x2); ②2(3b2-a3b)-3(2b2-a2b-a3b)-4a2b. 答案:①原式=3x2+1.②原式=a3b-a2b. (2)求多项式-x3-2x2+3x-1与-2x2+3x-2的差. 答案:-x3-2x2+3x-1-(-2x2+3x-2)=-x3-2x2+3x-1+2x2-3x+2=-x3+1. (3)在解“当x=-2,y=时,求x-2(x-y2)+(-x+y2)的值”时,甲同学不小心把“y=”写成“y=-”,但计算结果也是正确的,这是为什么? 答案:原式=x-2x+y2-x+y2=-3x+y2. 由于化简之后的式子中只含有y2,与y的正负性无关,所以y的符号不影响式子的最终结果. (4)小雯乘公共汽车到图书城买书,上车后发现车上共有(3a-b)人,车到中途站时,下车一半人,但又上车若干人,这时车上共有乘客(8a-5b)人,问: ①中途上车的乘客是多少人? ②当a=4,b=2时,上车乘客是多少人? 解:①(8a-5b)-(3a-b)=8a-5b-a+b=a-b. 答:中途上车的乘客是(a-b)人. ②当a=4,b=2时, 原式=×4-×2=17(人). 答:上车乘客是17人. 5.课堂小结,自我完善 (1)整式加减的运算法则; (2)整式加减的实质; (3)整式加减的结果:整式. (4)整式加减解决实际问题的一般步骤. 你还有什么疑问? 6.布置作业 课本P101练习1-3,P102习题4.2第5-8题. 用生活中常见到的上下车的例子导入新课,有亲切感,学生容易接受,学生急于用自己学到的数学知识解决实际问题,激发学生学习的兴趣. 充分有效地复习前面所学的主要内容,有利于学生顺利观察归纳出整式加减的实质,即整式的加减运算是“去括号”与“合并同类项”. 理解整式的加减运算法则,掌握整式的加减的运算方法. 例题的讲解,让学生巩固所学的知识. 在本单元最后一个课时设置一道难度稍大的例题,让学生掌握的知识得到升华. 巩固整式加减运算法则,培养学生的列式计算能力,同时使学生体会到数学来源于生活,应用于生活的价值美. 进一步巩固新知,及时检测学习效果. 利用整式加减解决实际问题. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 整式的加减 整式加减的运算法则: 几个整式相加减,如果有括号就先去括号,然后再合并同类项. 整式加减解决实际问题的一般步骤: (1) 根据题意列代数式; (2) 去括号、合并同类项; (3) 得出最后结果. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
21世纪教育网(www.21cnjy.com)
单 元 备 课
第 4单元 本单元所需课时数 6课时
课标要求 1.理解整式的概念. 2.掌握合并同类项的和去括号的法则. 3.能进行简单的整式加减运算.
教材分析 本章内容的编写是在学生已有的代数式(上一章)以及有理数运算的基础上展开的.整式的加减运算是学习下一章“一元一次方程”的直接基础,也是以后学习整式的乘除、分式和根式运算、方程以及函数等知识的基础.同时,也是学习物理、化学等学科及其他科学技术不可缺少的数学工具.
主要内容 本章的主要内容是整式的有关概念及整式的加减运算.主要包括两节:第4.1节“整式”主要介绍单项式、多项式、整式及其相关概念,第4.2节“整式的加法与减法”是在学习合并同类项和去括号的基础上,研究整式加减的运算法则.
教学目标 1.理解单项式、多项式、整式等概念,弄清它们之间的区别与联系. 2.理解同类项的概念,掌握合并同类项的方法,掌握去括号时符号的变化规律,能正确地进行同类项的合并和去括号.在准确判断、正确合并同类项的基础上,进行整式的加减运算. 3.理解合并同类项、去括号的依据是分配律;理解数的运算律和运算性质在整式的加减运算中仍然成立.
知识结构
课时分配 4.1 整 式 2课时 4.2 整式的加法与减法 3课时 教学活动 小结 1课时
教与学建议 1.加强式与数的类比教学. 2.抓住重点、加强练习,打好基础.
4.1 整式
第1课时
课题 单项式 课型 新授课
教学内容 教材第89-91页的内容
教学目标 1.理解单项式的概念,掌握单项式的系数和次数的概念,能判断一个代数式是不是单项式,对于一个单项式能说出它的系数和次数. 2.再进一步理解用字母表示数量关系的过程中建立符号意识,激发学生学习数学的积极性.
教学重难点 教学重点:单项式、单项式的系数和次数的概念. 教学难点:用字母表示数量关系及理解与单项式有关的概念.
教学活动
教学过程 备 注
1.创设情境,引入课题 【问题1】我们来看引言和上一章中遇到过的一些代数式 92t,a2,0.9p,a2h, 这些代数式有什么共同特点? 【师生活动】学生尝试解答,教师总结归纳. 2.类比探究,学习新知 【探究1】单项式的相关概念 【问题2】单项式的判断: 判断下列各式是否是单项式,是的打“√”,不是的打“×”,并说明理由. (1)m;(2)-9;(3)-2xy;(4)x+1;(5)2a-b; (6);(7);(8)9πx2;(9);(10). 【师生活动】学生尝试解答,教师总结单项式的概念. 总结:数或字母的积组成的式子叫作单项式,单独的一个数或一个字母也是单项式. 【问题3】确定单项式的系数和次数: 单项式4x6a2a3-nvt2πRx2yz次数
【师生活动】先由学生归纳总结,再由教师补充纠错. 总结:(1)一个单项式中,所有字母的指数的和叫作这个单项式的次数. (2)单项式次数只与字母指数有关(π是常数). 【探究2】单项式的应用 【问题4】用单项式填空,并指出它们的系数和次数. 1每包书有12册,n包书有 册. 2.底边长为a,高为h的三角形的面积是 . 3.一个长方体的长和宽都是a,高为h,它的体积是 . 4.一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为 . 5.一个长方形的长为0.9,宽为a,面积是 . 【问题5】用字母表示数后,同一个代数式在不同的问题中可以表示不同的含义.例如,在问题4,5中,所填的结果都是0.9a,一个是表示电视机的售价,一个表示长方形的面积,你还能赋予0.9a一个含义吗?(学生回答) 【师生活动】先由学生归纳总结,再由教师补充纠错. 3.学以致用,应用新知 例1下列各式中,哪些是单项式? x,-a3,,a,0.4x+3,a2+b+7,. 解:单项式有x,-a3,a. 例2写出下列各单项式的系数和次数: 30a-x3yab2c3-πr2系数次数
答案: 30a-x3yab2c3-πr2系数30-111-π次数131642
4.随堂训练,巩固新知 (1)在代数式,x+1,-2,-,0.72xy,,中,单项式有( ) A.2个 B.3个 C.4个 D.5个 答案:C (2)下列说法中,正确的是( ) A.0不是单项式 B.-的系数是-3 C.-的系数是- D.的次数是2 答案:D (3)用单项式填空: ①一辆汽车的速度是v千米/时,行驶t小时所走过的路程为_____千米; ②王洁同学买2本练习本花了n元,那么买m本练习本要_____元; ③边长为a的正方体的表面积为_____,正方体的体积为_____. 答案:①vt;②;③6a2;a3. 5.课堂小结,自我完善 教师与学生一起回顾本节课所学主要内容,并请学生回答以下问题:
(1)本节课学习了哪些主要内容? (2)判断单项式的系数和次数需要注意什么?
(3)你还有什么疑惑? 6.布置作业 课本P91练习1-2. 培养学生观察、发现的能力,总结出单项式的概念. 由浅入深,使学生透彻理解单项式的有关概念,培养他们应用新知识解决问题的能力. 熟知三角形,长方形面积公式. 例题的讲解,让学生巩固所学的新知识. 明确单项式的概念解决问题. 进一步巩固新知,及时检测学习效果. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 单项式 1.单项式的概念:数或字母的积 2.单项式的系数:数字因数 3.单项式的次数:所有字母的指数和 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.1 整式
第2课时
课题 多项式及整式 课型 新授课
教学内容 教材第91-93页的内容
教学目标 1.通过本节课的学习,学生掌握整式、多项式的项及其次数、常数项的概念. 2.知道整式和单项式、多项式的关系. 3.由单项式与多项式归纳出整式,这样更有利于学生把握概念的内涵与外延,有利于学生知识的迁移和知识结构体系的更新.
教学重难点 教学重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数,以及常数项等概念. 教学难点:多项式的次数.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 【问题1】你能指出下面哪些式子是单项式吗?并指出单项式的系数与次数. 3,π,a2b,,a2+b2,2+b. 【师生活动】由学生思考好后举手回答,锻炼他们的口答能力.单项式π的系数与次数比较容易错,教师适当解析. 【问题2】观察v+2.5,v-2.5,3x+5y+2z,ab-πr2,x2+2x+18,这些式子有什么特点? 【师生活动】由学生小组合作交流,教师肯定每一位学生说出的特点.如果学生仍然有困难,教师给予提示: (1)上面的式子是单项式吗? (2)这些式子与单项式有联系吗? 2.类比探究,学习新知 【问题3】什么叫多项式? 【师生活动】几个单项式的和叫作多项式. 【问题4】什么叫多项式的项和次数?多项式x2+2x+18是几次几项式? 【师生活动】在多项式中,每个单项式叫作多项式的项.不含字母的项叫作常数项.一个多项式含有几项,就叫几项式. 多项式里,次数最高的项的次数,叫作这个多项式的次数. x2+2x+18是二次三项式. 【问题5】下列多项式的项和次数分别是什么? v+2.5,3x+5y+2z,ab-πr2. 【师生活动】v+2.5的项分别是v,2.5,次数是1;3x+5y+2z的项分别是3x,5y,2z,次数是1;ab-πr2的项分别是ab,-πr2,次数是2. 【问题6】你认为确定多项式的项、次数时应注意什么? 【师生活动】①多项式的项应包括该项的符号;②多项式的次数为最高次项的次数;③常数项是多项式中的特殊项,确定多项式项数时不要漏掉. 【问题7】什么叫整式?下列式子哪些是整式? ①-x;②x+1;③π;④-3;⑤-+25. 【师生活动】出示自学提纲,让学生按要求自学教科书内容,独立解决相关问题.教师进行巡视,关注对于概念理解还不太透彻的学生;板书多项式、整式有关概念,强调:(1)多项式的项应包括该项的符号;(2)多项式的次数为最高次项的次数;(3)常数项是多项式中的特殊项,确定多项式项数时不要漏掉. 3.学以致用,应用新知 例1 下列式子中,哪些是整式?哪些是单项式?哪些是多项式? a,ax2+bx+c,-5,π,,. 解:单项式:a,-5,π. 多项式:ax2+bx+c,. 整式:a,ax2+bx+c,-5,π,. 例2 指出下列多项式的次数与项: (1)xy-; (2)a2+2a2b+ab2-b2; (3)2m3n3-3m2n2+mn. 解:(1)次数:2,项:xy,-. (2)次数:3,项:a2,2a2b,ab2,-b2. (3)次数:6,项:2m3n3,-3m2n2,mn. 例3 若多项式-x2y2n+1z+x2y+4是八次三项式,则n=_______. 答案:2 例4 如图,用式子表示圆环的面积,当R=15 cm,r=10 cm时,求圆环的面积(π取3.14). 解:外圆的面积减去内圆的面积就是圆环的面积,所以圆环的面积是πR2-πr2. 当R=15 cm,r=10 cm时,圆环的面积是 πR2-πr2=3.14×152-3.14×102=392.5(cm2). 答:这个圆环的面积是392.5 cm2. 4.随堂训练,巩固新知 (1)把下列各式的序号填在相应的集合里. ①0;②x2;③-x2-2x+5;④;⑤xy;⑥8+;⑦-5;⑧. 整式:{ ,…} 多项式:{ ,…} 单项式:{ ,…} 答案:整式:{①②③④⑤⑥⑦⑧,…} 多项式:{③⑥⑧,…} 单项式:{①②④⑤⑦,…} (2)指出下列多项式的项和次数. ①a3-a2b+ab2-b3;②3n4-2n2+1. 答案:①项:a3,-a2b,ab2,-b3,次数:3. ②项:3n4,-2n2,1,次数:4. (3)指出下列多项式是几次几项式: ①x3-x+1; ②x3-2x2y2+3y2. 答案:①三次三项式.②四次三项式. (4)a,b分别表示梯形的上底和下底,h表示梯形的高,则梯形的面积S=__________,当a=2 cm,b=4 cm,h=5 cm时,S=_________cm2. 答案:(a+b)h;15 5.课堂小结,自我完善 (1)多项式的定义: 几个单项式的和叫作多项式. (2)多项式的项和次数的定义: 在多项式中,每个单项式叫作多项式的项.不含字母的项叫作常数项. 多项式里,次数最高项的次数,就是这个多项式的次数. (3)注意:①多项式的项是应包括该项的符号;②多项式的次数为最高次项的次数;③常数项是多项式中的特殊项,确定多项式项数时不要漏掉. (4)整式的定义: 单项式与多项式统称整式. 6.布置作业 课本P93练习1-3. 通过简单的复习单项式的相关概念,为探究、学习多项式的相关概念打下坚实的基础. 以问题串的形式创设情境,引起学生的认知冲突,使学生对新知识产生好奇,从而激发学生的学习兴趣和求知欲望. 由浅入深,使学生对多项式的有关概念的理解更加透彻,培养他们应用新知识解决问题的能力. 1.了解单项式、多项式、整式的相关概念,会判断单项式、整式、多项式. 2.会判断多项式的次数和项数. 3.巩固多项式的概念,同时为学生创造用多项式表示实际问题中的数量关系的机会,培养学生的列式能力,同时使学生体会到数学来源于生活,应用于生活的价值美. 考查整式的分类. 熟知并理解多项式的项和次数的概念. 会判断多项式项数与次数. 用多项式表示数量关系. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用.
板书设计 多项式及整式 1.多项式的定义:几个单项式的和叫作多项式. 2.多项式的项和次数的定义: 在多项式中,每个单项式叫作多项式的项.不含字母的项叫作常数项. 多项式里,次数最高的项的次数,叫作这个多项式的次数. 3.整式的定义: 单项式与多项式统称整式. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.2 整式的加法与减法
第1课时
课题 合并同类项 课型 新授课
教学内容 教材第95-98页的内容
教学目标 1.了解同类项及合并同类项的概念. 2.通过类比数的运算探究合并同类项的法则,从中体会“数式通性”和类比的思想,培养学生观察、探索、分类、归纳的能力.
教学重难点 教学重点:理解同类项的概念及合并同类项法则. 教学难点:正确判断同类项,准确合并同类项.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 【问题1】汽车从香港口岸到西人工岛包含两段路程,一段为香港口岸到东人工岛,另一段为海底隧道.如果汽车通过海底隧道需要a h,那么从香港口岸到东人工岛所需时间是1.25a h,香港口岸到西人工岛的全长(单位:km)是多少呢? 【师生活动】学生尝试解答,得到香港口岸到西人工岛的全长为72a+96×1.25a=72a+120a. 教师追问:这个式子还能化简吗? 2.类比探究,学习新知 类比数的运算,我们应如何化简式子72a+120a? 【问题2】(1)运用运算律计算: 72×2+120×2= , 72×(-2)+120×(-2)= ; (2)根据(1)中的方法完成下面的运算: 72a+120a = . 【师生活动】根据分配律,可得72×2+120×2=(72+120)×2=192×2=384; 72×(-2)+120×(-2)=(72+120)×(-2)=-384. 教师提问:式子72a+120a与(1)中的两个算式有什么联系? 根据学生的回答情况引导归纳:算式72×2+120×2与72×(-2)+120×(-2)和式子72a+120a具有相同的结构,并且字母t代表的是一个因(乘)数,因此根据分配律应有72a+120a=(72+120)a=192a. 【问题3】类比式子72a+120a的化简方法,填空: (1)72a-120a=( )a; (2)3m2+2m2=( )m2; (3)3xy2-4xy2=( )xy2. 【师生活动】利用分配律可得: 72a-120a=(72-120)a=-48a,3m2+2m2=(3+2)m2=5m2, 3xy2-4xy2=(3-4)xy2=-xy2. 在计算72a-120a时,注意分配律的使用:72a-120a=[72+(-120)]a=(72-120)a. 【问题4】(1)观察多项式72a+120a,72a-120a,3m2+2m2,3xy2-4xy2,各多项式的项有什么共同特点? (2)通过以上化简计算,你能从中得出什么规律? 【师生活动】每个式子的项含有相同的字母;相同字母的指数也相同.根据分配律把多项式各项的系数相加,字母部分保持不变. 在讨论交流的基础上,教师引导学生归纳同类项的定义、合并同类项的定义和法则. 像72a与-120a,3m2与2m2,3xy2与4xy2这样,所含字母相同,并且相同字母的指数也相同的项叫作同类项.几个常数项也是同类项. 把多项式中的同类项合并成一项,叫作合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的和,字母连同它的指数不变. 【问题5】找出多项式4x2+2x+7+3x-8x2-2中的同类项,并进行合并,由此归纳出化简多项式的一般步骤. 【师生活动】教师引导学生口述,教师给出板书演示. 4x2+2x+7+3x-8x2-2 =4x2-8x2+2x+3x+7-2 (交换律) =(4x2-8x2)+(2x+3x)+(7-2) (结合律) =(4-8)x2+(2+3)x+(7-2) (分配律) =-4 x2+5x+5. 找出同类项并做不同的标记,运用交换律、结合律分配律把同类项结合并合并,最后按某个字母的降幂或升幂排列. 3.学以致用,应用新知 【例1】下列各组单项式,是同类项的是( ) A.2ab2与a2b B.-x与y C.3与3a D.-x3y2与-3x3y2 答案:D 【变式】已知单项式3xmy3与-4x5y3是同类项,则m= . 答案:5 【例2】合并下列各式的同类项: (1)xy2-xy2; (2)-3x2y+2x2y+3x2y-2x2y; (3)4a2+3b2+2ab-4a2-4b2. 答案:(1)xy2-xy2=xy2;(2)-3x2y+2x2y+3x2y-2x2y=- x2y+ xy2;(3)4a2+3b2+2ab-4a2-4b2=- b2+2ab. 【例3】求多项式2x2-5x+x2+4x-3x2-2的值,其中x=. 答案:- 【变式】求多项式3a+abc-c2-3a+c2的值,其中a=-,b=2,c=-3。 答案:1 【例4】(1)水库水位第一天连续下降了a h,每小时平均下降2cm;第二天连续上升了a h,每小时平均上升0.5cm,这两天水位总的变化情况如何? (2)某商店原有5袋大米,每袋大米为x kg.上午售出3袋,下午又购进同样包装的大米4袋.进货后这个商店有大米多少千克? 答案:(1)-2a+0.5a=-1.5a.(2)5x-3x+4x=6x. 4.随堂训练,巩固新知 (1)下列单项式中,与a3b2是同类项的是( ) A.- a2b3 B.2a3b2 C.- ab4 D. a4b 答案:B (2)下列运算正确的是( ) A.3a+2a=5 B.3a-2a=1 C. 3a-2a=a D. 3a-2a=6a 答案:C (3)化简:①-2ab+6ab-(-8ab);②4xy-3x2-3xy+2x2。 答案:①12ab;②xy- x2. (4)求下列各式的值: ①4a2+2a+1-3a2-3a,其中a=-1;②4xy-3x2-3xy-2y+3x2,其中x=-1,y=-3. 答案:①3;②9. (5)已知2xmy与3x2yn-1的和是单项式,求m,n的值. 答案:m=2,n=2. 5.课堂小结,自我完善 (1)判断同类项的两条标准:所含字母相同;相同字母的指数也相同 (2)合并同类项后,所得项的系数是合并前各同类项的系数的和,字母连同它的部分不变. (3)多项式中合并同类项的步骤:①找出同类项做出标记;②运用交换律、结合律将多项式的同类项结合;③运用分配律合并同类项;④按同一个字母的降幂(或升幂)排列. 6.布置作业 课本P98练习1-3,P102习题4.2第1题. 引入实际问题,使学生感受到学习含有字母的式子的运算是实际需要.此环节教师应关注学生是否能正确列式,得出正确的式子,从而引出对合并同类项法则的探讨. 通过用分配律进行有理数的运算,帮助理解用分配律化简式子72a+120a的方法,为进一步类比学习整式的运算提供方法上的借鉴.通过引导学生观察比较,发现三个算式的联系,体会由“数”到“式”是由特殊到一般的思想方法,初步感受“数式通性”和类比的数学思想. 教师应关注学生是否正确区分运算符号和性质符号.通过几组不同形式的同类项,感受不同类型式子的组成,突出同类项的特点,为归纳同类项的概念和合并同类项法则做好铺垫. 在观察、比较中,发现各多项式的共同特征,分析运算特点,归纳出同类项、合并同类项及合并同类项的法则. 归纳化简多项式的一般步骤,规范学生的解题过程,避免出现漏项等易错点,帮助学生快速掌握化简多项式的方法. 加深学生对同类项的概念和合并同类项法则的理解和运用,提高运算能力. 在求多项式的值时,先化简再代入求值往往可以简化计算. 通过让学生解决生活中的实际问题,进一步理解合并同类项的概念及法则,培养计算能力,激发学习兴趣. 正确理解同类项的概念. 掌握合并同类项法则. 两个单项式的和还是单项式等同于这两个单项式是同类项. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 合并同类项 概念 同类项 举例 概念 合并同类项 法则 应用 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.2 整式的加法与减法
第2课时
课题 去括号 课型 新授课
教学内容 教材第98-100页的内容
教学目标 1.学生经过观察、合作交流、讨论总结出去括号的法则,并掌握. 2.能正确且较为熟练地运用去括号法则化简代数式. 3.经历带有括号的有理数的运算,发现去括号时符号变化的规律,归纳出去括号法则,培养学生观察、分析、归纳能力,发展学生的数学思维.
教学重难点 教学重点:准确应用去括号法则将整式化简. 教学难点:准确应用去括号法则将整式化简.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 用火柴棒搭正方形时,怎样计算所需要的火柴棒的根数吗?拿出准备好的火柴棒,自己搭一下,然后再按如下做法搭. 小明的做法: 第一个正方形用4根火柴棒,每增加一个正方形增加3根火柴棒,那么搭x个正方形就需要火柴棒[4+3(x-1)]根. 小颖的做法: 每一个正方形可以看成是用4根火柴棒搭成的,然后再减去多算的根数,就得到搭x个正方形需要的火柴棒根数是4x-(x-1). 小刚的做法: 第一个正方形可以看成是用3根火柴增加1根火柴棒搭成的,此后每增加一个正方形就增加3根火柴棒,那么搭x个正方形共需(3x+1)根火柴棒. 他们的做法都正确吗?你能解释吗? 2.类比探究,学习新知 【探究】去括号法则 本章引言中的问题(3). 汽车通过主桥的行驶时间是b h,那么汽车在主桥上行驶的路程是92b km;通过海底隧道所需时间比通过主桥的时间少0.15 h,那么汽车在海底隧道行驶的时间是(b-0.15)h,行驶的路程是72(b-0.15)km.因此,主桥与海底隧道长度的和(单位:km)为92b+72(b-0.15), 主桥与海底隧道长度的差(单位:km)为92b-72(b-0.15). 观察上面的两个式子,你们知道该怎样化简吗 【师生活动】教师指导学生解答问题,师生共同讨论、交流,最后由老师归纳总结出去括号的方法. 一般地,一个数与一个多项式相乘,需要去括号,去括号就是用括号外的数乘括号内的每一项,再把所得的积相加. 注意:(1)去括号时改变了代数式的形式,但不改变代数式的值; (2)去括号时用括号外的数乘括号内的每一项,不要漏乘. 3.学以致用,应用新知 例1 化简下列各式: (1)x-(3x-2)+(2x+3); (2)(3a2+a-5)-(4-a+7a2); (3)(2m-3)+m-(3m-2); (4)3(4x-2y)-3(-y+8x). 答案:(1)5.(2)-4a2+2a-9.(3)-1.(4)-12x-3y. 例2 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是 a km/h. (1)2 h后两船相距多远? (2)2 h后甲船比乙船多航行多少千米? 解:顺水航速=船速+水速=(50+a) km/h, 逆水航速=船速-水速=(50-a) km/h. (1)2 h后两船相距(单位:km) 2(50+a)+2(50-a)=100+2a+100-2a=200. (2)2 h后甲船比乙船多航行(单位:km) 2(50+a)-2(50-a)=100+2a-100+2a=4a. 4.随堂训练,巩固新知 (1)-(x-2y+3z)去括号后的结果为( ) A.x-2y+3z B.-x+2y-3z C.x+2y-3z D.-x+2y+3z 答案:B (2)下列各式中,去括号正确的是( ) A.x2-(x-y+2z)=x2-x+y+2z B.x-(-2x+3y-1)=x+2x+3y+1 C.3x+2(x-2y+1)=3x-2x-2y-2 D.-(x-2)-2(x2+2)=-x+2-2x2-4 答案:D (3)化简: ①5a-(2a-4b); ②2x2+3(2x-x2); ③6a2-4ab-4(2a2+ab);④-3(2x2-xy)+4(x2+xy-6). 解:①原式=3a+4b.②原式=-x2+6x. ③原式=-2a2-6ab.④原式=-2x2+7xy-24. (4)先化简,再求值:(4a2-3a)-(2a2+a-1)+(2-a2)+4a,其中a=-2. 解:原式=a2+3.当a=-2时,原式=(-2)2+3=7. 5.课堂小结,自我完善 教师与学生一起回顾本节课所学主要内容,并请学生回答以下问题:
(1)本节课学习了哪些主要内容? (2)去括号时需要注意什么?
(3)你还有什么疑惑? 6.布置作业 课本P100练习1-4,P102习题4.2第2-4题. 让学生经历动手实践,将实际问题抽象为数学问题的过程,感受数学知识与生活的联系,激发学生的学习兴趣,也为新课的学习做好铺垫. 深入思考,培养学生逆向思维的习惯,从而更进一步加深学生对去括号法则的理解. 可以让学生先独立尝试解决,然后通过学生反馈的情况,教师针对一些存在的问题进行示范性讲解并板书. 运用所归纳的知识解决问题,提高学生解决问题的能力. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 去括号法则 一般地,一个数与一个多项式相乘,需要去括号,去括号就是用括号外的数乘括号内的每一项,再把所得的积相加. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
4.2 整式的加法与减法
第3课时
课题 整式的加减 课型 新授课
教学内容 教材第100-101页的内容
教学目标 1.能根据题意列出式子,会用整式加减的运算法则进行整式加减运算,并能说明其中的算理. 2.经历用字母表示实际问题中的数量关系的过程,发展符号感,提高运算能力及综合运用知识进行分析、解决问题的能力,发展数学思维.
教学重难点 教学重点:列式表示实际问题中的数量关系,会用整式加减的运算法则进行整式加减运算. 教学难点:列式表示问题中的数量关系,整式加减的运算法则的运用.
教学活动
教 学 过 程 备 注
1.创设情境,引入课题 小明乘公共汽车到城里的书店买书,小明上车时,发现车上已有(3a-b)人,车到中途站时,有(2a-3)人下车,但又上来若干人,这时公共汽车上共有(8a-5b)人,则中途有多少人上车? 你能用学到的数学知识解决这个实际问题吗? 现在我们一起来分析一下: 要计算中途上车的人数,可用总人数减去下车后剩下的人数,因为原来有(3a-b)人,加上小明,所以没人下车之前,车上共有(3a-b+1)人,下去(2a-3)人后,车里还有(3a-b+1)-(2a-3)=(a-b+4)人,用总人数(8a-5b)减去(a-b+4)即可求出上车的人数. 这就是我们今天要学习的整式的加减.如何进行整式的加减呢? 【师生活动】师生一起分析完,让学生自己列出式子(8a-5b)-[(3a-b+1)-(2a-3)]表示中途上车的人数.如果学生列出式子有困难的话,教师要给予一定的提示或者师生共同列出式子. 2.类比探究,学习新知 【问题1】做大小两个长方体纸盒,尺寸如下(单位:cm): 长宽高小纸盒abc大纸盒1.5a2b2c
(1)做这两个纸盒共用纸多少平方厘米? (2)做大纸盒比做小纸盒多用纸多少平方厘米? 【问题2】求x-2(x-y2)+(-x+y2)的值,其中x= -2,y=. 【问题3】化简: (1)(x+y)-(2x-3y); (2)2(a2-2b2)-3(2a2+b2). 以上化简实际上进行了哪些运算? 【师生活动】教师指导学生解答问题,师生共同讨论、交流,最后由教师归纳总结出整式加减的运算法则: 几个整式相加减,如果有括号就先去括号,然后再合并同类项. 【问题4】笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2 支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱? 答案:小红和小明买笔记本共花费(3x+4x)元,圆珠笔共花费(2y+3y)元. 小红和小明一共花费(单位:元) (3x+4x) + (2y+3y) = 7x+5y. 【师生活动】教师指导学生解答问题,师生共同讨论、交流,最后由教师归纳总结出整式加减解决实际问题的一般步骤. (1) 根据题意列代数式; (2) 去括号、合并同类项; (3) 得出最后结果. 3.学以致用,应用新知 【例1】(1)3a+2-(-4a); (2)(ab-3a2)-2b2-5ab-(a2-2ab); 解:(1)原式=7a+2.(2)原式=-4a2-2b2-2ab. 【例2】先化简再求值: ,其中. 解:(1)﹣(9x3﹣4x2+5)﹣(﹣3﹣8x3+3x2) =﹣9x3+4x2﹣5+3+8x3﹣3x2 =﹣x3+x2﹣2 当x=2时,原式=﹣23+22﹣2=﹣6 4.随堂训练,巩固新知 (1)①2(x2+3)-(5-x2); ②2(3b2-a3b)-3(2b2-a2b-a3b)-4a2b. 答案:①原式=3x2+1.②原式=a3b-a2b. (2)求多项式-x3-2x2+3x-1与-2x2+3x-2的差. 答案:-x3-2x2+3x-1-(-2x2+3x-2)=-x3-2x2+3x-1+2x2-3x+2=-x3+1. (3)在解“当x=-2,y=时,求x-2(x-y2)+(-x+y2)的值”时,甲同学不小心把“y=”写成“y=-”,但计算结果也是正确的,这是为什么? 答案:原式=x-2x+y2-x+y2=-3x+y2. 由于化简之后的式子中只含有y2,与y的正负性无关,所以y的符号不影响式子的最终结果. (4)小雯乘公共汽车到图书城买书,上车后发现车上共有(3a-b)人,车到中途站时,下车一半人,但又上车若干人,这时车上共有乘客(8a-5b)人,问: ①中途上车的乘客是多少人? ②当a=4,b=2时,上车乘客是多少人? 解:①(8a-5b)-(3a-b)=8a-5b-a+b=a-b. 答:中途上车的乘客是(a-b)人. ②当a=4,b=2时, 原式=×4-×2=17(人). 答:上车乘客是17人. 5.课堂小结,自我完善 (1)整式加减的运算法则; (2)整式加减的实质; (3)整式加减的结果:整式. (4)整式加减解决实际问题的一般步骤. 你还有什么疑问? 6.布置作业 课本P101练习1-3,P102习题4.2第5-8题. 用生活中常见到的上下车的例子导入新课,有亲切感,学生容易接受,学生急于用自己学到的数学知识解决实际问题,激发学生学习的兴趣. 充分有效地复习前面所学的主要内容,有利于学生顺利观察归纳出整式加减的实质,即整式的加减运算是“去括号”与“合并同类项”. 理解整式的加减运算法则,掌握整式的加减的运算方法. 例题的讲解,让学生巩固所学的知识. 在本单元最后一个课时设置一道难度稍大的例题,让学生掌握的知识得到升华. 巩固整式加减运算法则,培养学生的列式计算能力,同时使学生体会到数学来源于生活,应用于生活的价值美. 进一步巩固新知,及时检测学习效果. 利用整式加减解决实际问题. 通过小结,帮助学生梳理本节课所学内容,强化记忆,课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 整式的加减 整式加减的运算法则: 几个整式相加减,如果有括号就先去括号,然后再合并同类项. 整式加减解决实际问题的一般步骤: (1) 根据题意列代数式; (2) 去括号、合并同类项; (3) 得出最后结果. 提纲挈领,重点突出.
教后反思 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
21世纪教育网(www.21cnjy.com)
同课章节目录
