6.2.2 线段的比较与运算 课件(共31张PPT)
文档属性
| 名称 | 6.2.2 线段的比较与运算 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 05:49:30 | ||
图片预览








文档简介
(共31张PPT)
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2.了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
3. 理解线段等分点的意义.
4. 能够运用线段的和、差、倍、分关系求线段的长度.
1.理解线段等分点的意义.
2.能够运用线段的和、差、倍、分关系求线段的长度.
能够运用线段的和、差、倍、分关系求线段的长度.
难点
重点
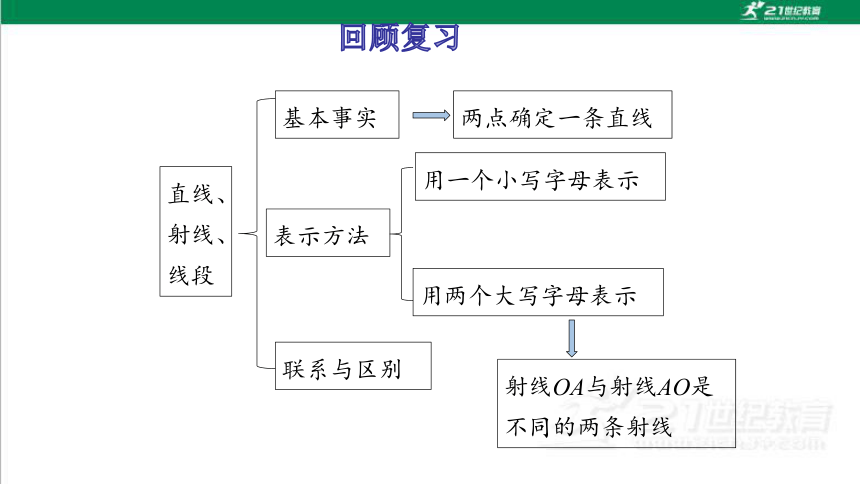
直线、射线、线段
基本事实
表示方法
两点确定一条直线
用一个小写字母表示
用两个大写字母表示
射线OA与射线AO是不同的两条射线
联系与区别
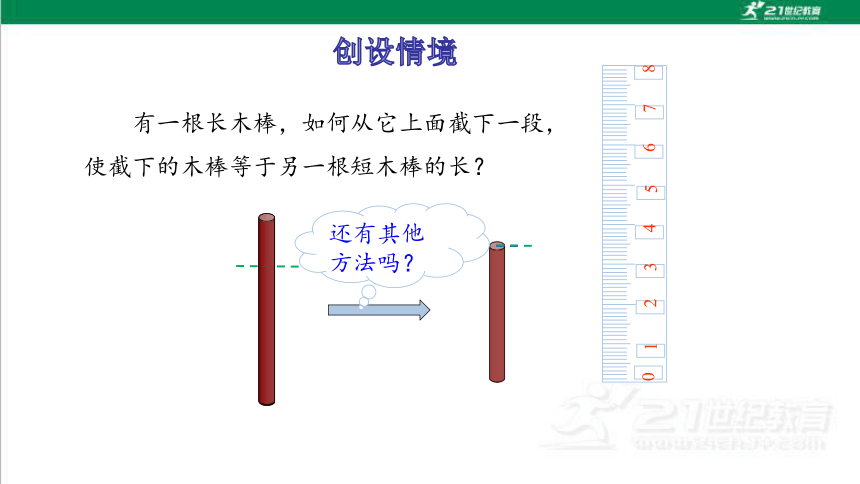
有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根短木棒的长?
还有其他方法吗?
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以下办法.
知识点1 线段的画法及长短比较
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
在可打开角度的最大范围内,圆规可截取任意长度,相当于可以移动的“小木棍”.
作一条线段等于已知线段.
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AC;
第二步:用圆规在射线 AC 上截取AB = a.
线段 AB 即为所求.
a
A C
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
比较两个同学高矮的方法:
——叠合法
②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的数值进行比较.
——度量法
试比较线段AB,CD的长短.
(1) 度量法:先利用刻度尺分别测量出两条直线的长度,然后根据测量结果进行比较;
(2) 叠合法:把两条线段中的一条线段移到另一条线段上,使它们有一个端点重合,然后根据另一个端点的位置进行比较.
C D
A B
C
D
(A)
B
<
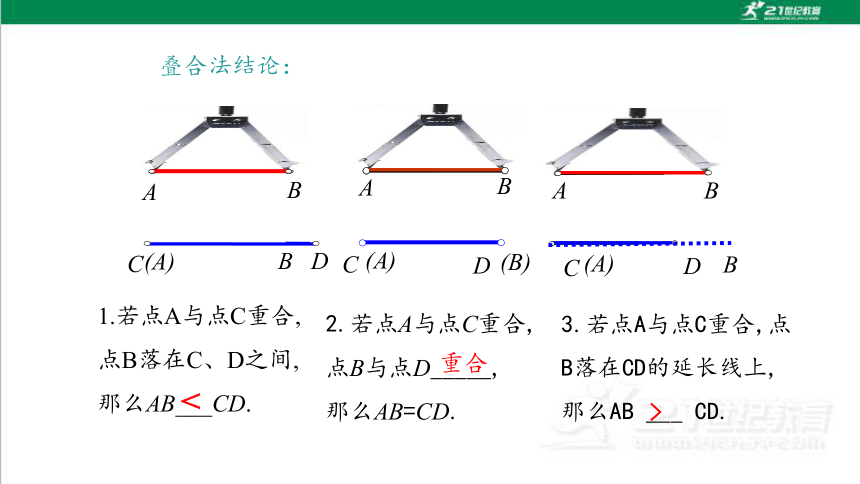
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
例1 下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
例2 比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
D
A
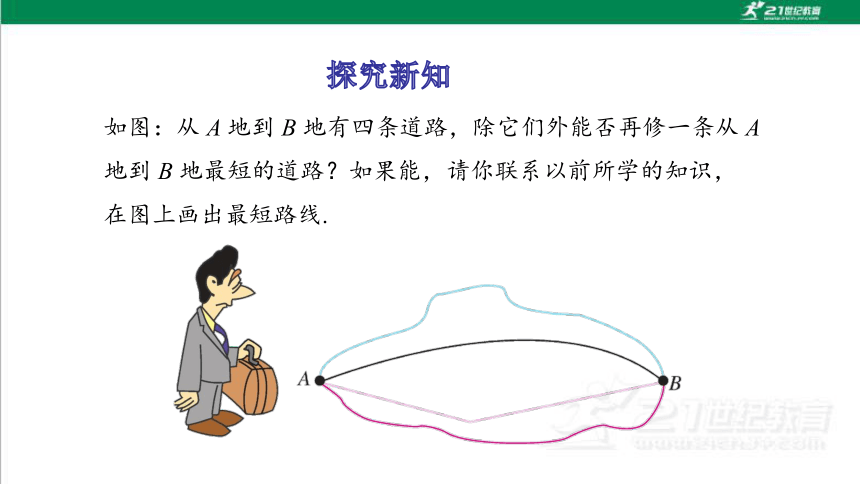
如图:从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地最短的道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
知识点2
关于线段的基本事实及两点的距离
经过比较,可以得到一个关于线段的基本事实:
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
你能举出这个基本事实在生活中的一些应用吗?
如图,这是 A,B 两地之间的公路,在公路工程改造计划时,为使 A,B 两地行程最短,应如何设计线路?请在图中画出,并说明理由.
B
A
.
两点之间线段最短.
如图,公园里修建了曲折迂回的桥,这与修一座直的桥相比,对游人观赏湖面风光能起到什么作用?用你所学数学知识说明其中的道理.
由于“两点之间,线段最短”,这样做增加桥的长度,一方面使这座桥能容纳更多的游人来观光,另一方面也增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光.
连接两点的线段的长度,叫作这两点间的距离.
注意:两点间的距离是指连接两点间的线段的长度,如 A,B 两点的距离是指线段AB 的长度,而不是线段 AB 本身.不能将 A,B 两点的距离说成线段 AB.
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B
B.A→C→F→B
C.A→C→E→F→B
D.A→C→M→B
例3
B
在直线上画出线段 AB=a ,再在 AB 的延长线上画线段 BC=b,线段 AC 就是 a 与 b 的和,记作 AC=a+b.
如果在 AB 上画线段 BD=b,那么线段 AD就是 a 与 b 的差,记作 AD= a-b.
A
B
C
D
a+b
a-b
a
b
b
线段的和差:
例4 如图,已知线段a,b,作一条线段,使它等于2a-b.
a
b
解:如图,在直线上作线段AB=a,再在线段AB的延长线上作线段BC=a,则线段AC上作线段CD=b,则线段AD=2a-b.
知识点3 线段的中点
在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?
中点
A
B
M
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫作线段 AB 的中点.
类似地,还有线段的三等分点、四等分点等.
(或 AB = 3AM = 3MN = 3NB)
N
M
B
A
线段的三等分点
(或 AB=4AO =4OP =4PQ=4QB)
线段的四等分点
A
O
P
Q
B
例5 如图所示,若BC =CD,则 BD = CD,BC = BD,BC CE,AC CD(最后两空填“>”“<”或“=”).
解:因为BC=CD,
所以BD= BC+ CD= CD +CD=2CD,
BC= CD= CE - DE< CE,
2
<
>
AC=AB +BC=AB + CD > CD.
1.尺规作图的工具是( )
A.刻度尺和圆规 B.三角尺和圆规
C.直尺和圆规 D.没有刻度的直尺和圆规
2.为了比较线段AB与CD的大小,小明将点A与点C重合,使两条线段在一条直线上,结果点B在CD的延长线上,则( )
A.AB<CD B.AB>CD
C.AB=CD D.以上都不对
D
B
3.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分,发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是 .
两点之间,线段最短
4. 如图,已知AB=8 cm,BD=3 cm,C为AB的中点,则线段CD的长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
A
5.已知线段AB=10 cm,点C是直线AB上一点,BC=4 cm,若M是AB的中点,N是BC的中点,则线段MN的长度是( )
A.7 cm B.3 cm C.7 cm或3 cm D.5 cm
C
1.如图,点 D 是线段 AB 的中点,点 C 是线段 AD 的中点,若 CD=1,则AB= .
解:因为点 C 是线段 AD 的中点,
所以 AD=2CD =2.
因为点 D 是线段 AB 的中点,
所以 AB=2AD=4.
4
A
C
D
B
2.如图,M 是线段 AC 的中点,点 B 在线段 AC 上,且 AB=4,BC=2AB,求线段 MC 和线段 BM 的长.
A
B
M
C
解:因为AB=4, BC=2AB,
所以BC=8,
所以AC=AB+BC=4+8=12.
因为M是线段AC的中点,
所以MC=AM= AC=6,
所以BM=AM-AB=6-4=2.
3.如图,已知线段 a,b,c,用直尺和圆规作线段 AB,使 AB=a+3b -c.
A
B
C
解:(1) 作射线 AM;
(2) 在射线 AM 上截取 AC=a;
(3) 在射线 CM 上连续截取 CD=DE=EF=b;
(4) 在线段 FA 上截取 FB=c.
则线段 AB 即为所求.
D
E
F
M
c
b
a
b
b
a
c
b
线段的
比较与运算
线段的比较
线段的和、
差、倍、分
度量法
叠合法
中点
思想方法
方程思想
分类思想
基本作图
关于线段的基本事实:
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
两点的距离:
连接两点间的线段的长度.
1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.
2.了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
3. 理解线段等分点的意义.
4. 能够运用线段的和、差、倍、分关系求线段的长度.
1.理解线段等分点的意义.
2.能够运用线段的和、差、倍、分关系求线段的长度.
能够运用线段的和、差、倍、分关系求线段的长度.
难点
重点
直线、射线、线段
基本事实
表示方法
两点确定一条直线
用一个小写字母表示
用两个大写字母表示
射线OA与射线AO是不同的两条射线
联系与区别
有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根短木棒的长?
还有其他方法吗?
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以下办法.
知识点1 线段的画法及长短比较
画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请大家想想办法,如何再画一条与它相等的线段?
在可打开角度的最大范围内,圆规可截取任意长度,相当于可以移动的“小木棍”.
作一条线段等于已知线段.
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AC;
第二步:用圆规在射线 AC 上截取AB = a.
线段 AB 即为所求.
a
A C
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
比较两个同学高矮的方法:
——叠合法
②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的数值进行比较.
——度量法
试比较线段AB,CD的长短.
(1) 度量法:先利用刻度尺分别测量出两条直线的长度,然后根据测量结果进行比较;
(2) 叠合法:把两条线段中的一条线段移到另一条线段上,使它们有一个端点重合,然后根据另一个端点的位置进行比较.
C D
A B
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
例1 下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
例2 比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
D
A
如图:从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地最短的道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
知识点2
关于线段的基本事实及两点的距离
经过比较,可以得到一个关于线段的基本事实:
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
你能举出这个基本事实在生活中的一些应用吗?
如图,这是 A,B 两地之间的公路,在公路工程改造计划时,为使 A,B 两地行程最短,应如何设计线路?请在图中画出,并说明理由.
B
A
.
两点之间线段最短.
如图,公园里修建了曲折迂回的桥,这与修一座直的桥相比,对游人观赏湖面风光能起到什么作用?用你所学数学知识说明其中的道理.
由于“两点之间,线段最短”,这样做增加桥的长度,一方面使这座桥能容纳更多的游人来观光,另一方面也增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光.
连接两点的线段的长度,叫作这两点间的距离.
注意:两点间的距离是指连接两点间的线段的长度,如 A,B 两点的距离是指线段AB 的长度,而不是线段 AB 本身.不能将 A,B 两点的距离说成线段 AB.
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B
B.A→C→F→B
C.A→C→E→F→B
D.A→C→M→B
例3
B
在直线上画出线段 AB=a ,再在 AB 的延长线上画线段 BC=b,线段 AC 就是 a 与 b 的和,记作 AC=a+b.
如果在 AB 上画线段 BD=b,那么线段 AD就是 a 与 b 的差,记作 AD= a-b.
A
B
C
D
a+b
a-b
a
b
b
线段的和差:
例4 如图,已知线段a,b,作一条线段,使它等于2a-b.
a
b
解:如图,在直线上作线段AB=a,再在线段AB的延长线上作线段BC=a,则线段AC上作线段CD=b,则线段AD=2a-b.
知识点3 线段的中点
在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?
中点
A
B
M
A
B
M
如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫作线段 AB 的中点.
类似地,还有线段的三等分点、四等分点等.
(或 AB = 3AM = 3MN = 3NB)
N
M
B
A
线段的三等分点
(或 AB=4AO =4OP =4PQ=4QB)
线段的四等分点
A
O
P
Q
B
例5 如图所示,若BC =CD,则 BD = CD,BC = BD,BC CE,AC CD(最后两空填“>”“<”或“=”).
解:因为BC=CD,
所以BD= BC+ CD= CD +CD=2CD,
BC= CD= CE - DE< CE,
2
<
>
AC=AB +BC=AB + CD > CD.
1.尺规作图的工具是( )
A.刻度尺和圆规 B.三角尺和圆规
C.直尺和圆规 D.没有刻度的直尺和圆规
2.为了比较线段AB与CD的大小,小明将点A与点C重合,使两条线段在一条直线上,结果点B在CD的延长线上,则( )
A.AB<CD B.AB>CD
C.AB=CD D.以上都不对
D
B
3.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分,发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是 .
两点之间,线段最短
4. 如图,已知AB=8 cm,BD=3 cm,C为AB的中点,则线段CD的长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
A
5.已知线段AB=10 cm,点C是直线AB上一点,BC=4 cm,若M是AB的中点,N是BC的中点,则线段MN的长度是( )
A.7 cm B.3 cm C.7 cm或3 cm D.5 cm
C
1.如图,点 D 是线段 AB 的中点,点 C 是线段 AD 的中点,若 CD=1,则AB= .
解:因为点 C 是线段 AD 的中点,
所以 AD=2CD =2.
因为点 D 是线段 AB 的中点,
所以 AB=2AD=4.
4
A
C
D
B
2.如图,M 是线段 AC 的中点,点 B 在线段 AC 上,且 AB=4,BC=2AB,求线段 MC 和线段 BM 的长.
A
B
M
C
解:因为AB=4, BC=2AB,
所以BC=8,
所以AC=AB+BC=4+8=12.
因为M是线段AC的中点,
所以MC=AM= AC=6,
所以BM=AM-AB=6-4=2.
3.如图,已知线段 a,b,c,用直尺和圆规作线段 AB,使 AB=a+3b -c.
A
B
C
解:(1) 作射线 AM;
(2) 在射线 AM 上截取 AC=a;
(3) 在射线 CM 上连续截取 CD=DE=EF=b;
(4) 在线段 FA 上截取 FB=c.
则线段 AB 即为所求.
D
E
F
M
c
b
a
b
b
a
c
b
线段的
比较与运算
线段的比较
线段的和、
差、倍、分
度量法
叠合法
中点
思想方法
方程思想
分类思想
基本作图
关于线段的基本事实:
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
两点的距离:
连接两点间的线段的长度.
同课章节目录
