6.3.1 角的概念 课件(共34张PPT)
文档属性
| 名称 | 6.3.1 角的概念 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 05:47:24 | ||
图片预览







文档简介
(共34张PPT)
1. 理解角的定义和相关概念,掌握角的表示方法.
2. 会正确使用量角器测量角的大小.
3. 认识角的单位,会进行度、分、秒之间的换算.
4.认识方位角.
理解角的定义和相关概念,掌握角的表示方法.
认识角的单位,会进行度、分、秒之间的换算.
难点
重点
有公共端点的两条射线组成的图形叫作角.
这个公共端点是角的顶点.
这两条射线是角的两条边.
顶点
边
我们小学阶段已经学过角的概念,想一想小学阶段我们是怎样定义角的?
观察下面实物,你发现这些实物给我们共同的形象是什么?
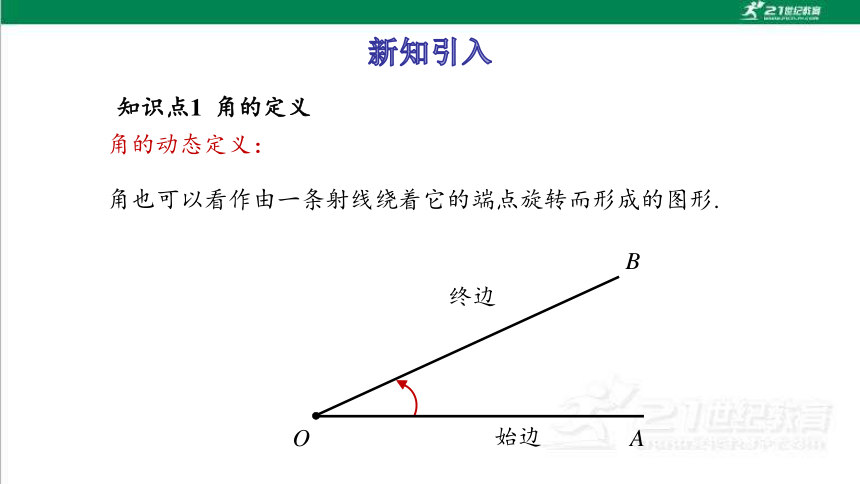
知识点1 角的定义
角的动态定义:
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
始边
终边
O
A
B
O
A
B
(B)
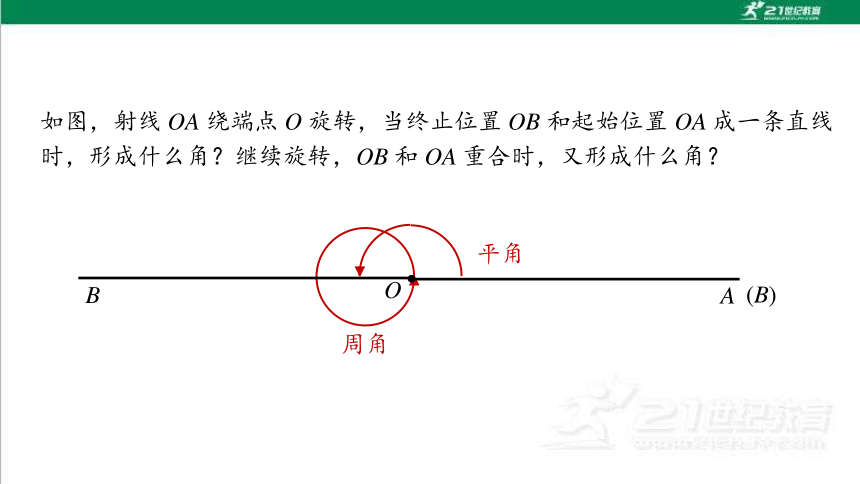
平角
周角
如图,射线 OA 绕端点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
注意:1. 我们平时画角时,只画角的一部分,角的两边是
两条射线.
2. 角的大小只与构成角的两边张开的幅度有关.
3. 平角的两边成一条直线,但不能说平角就是直线;
周角两边重合形成一条射线,但不能说周角就是射线.
例1 下列说法中,正确的是( )
A.两条射线所组成的图形叫作角
B.有公共点的两条射线叫作角
C.一条射线绕着它的端点旋转叫作角
D.一条射线绕着它的端点旋转而形成的图形叫作角
D
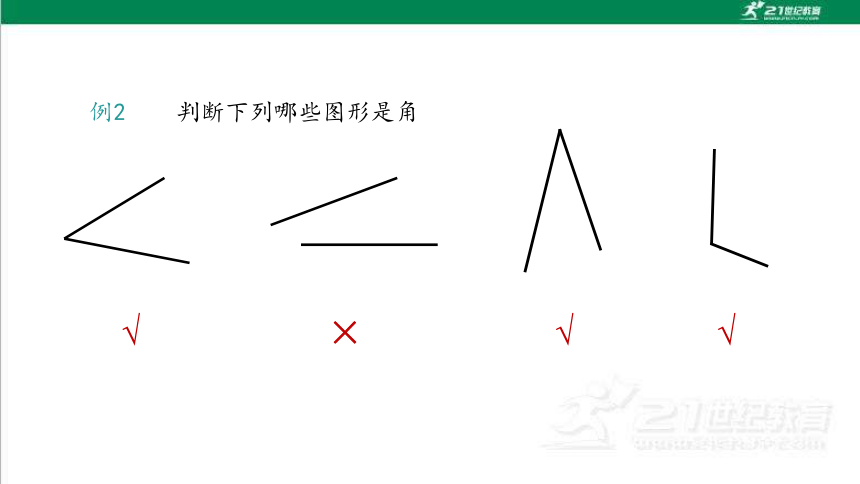
例2 判断下列哪些图形是角
√
×
√
√
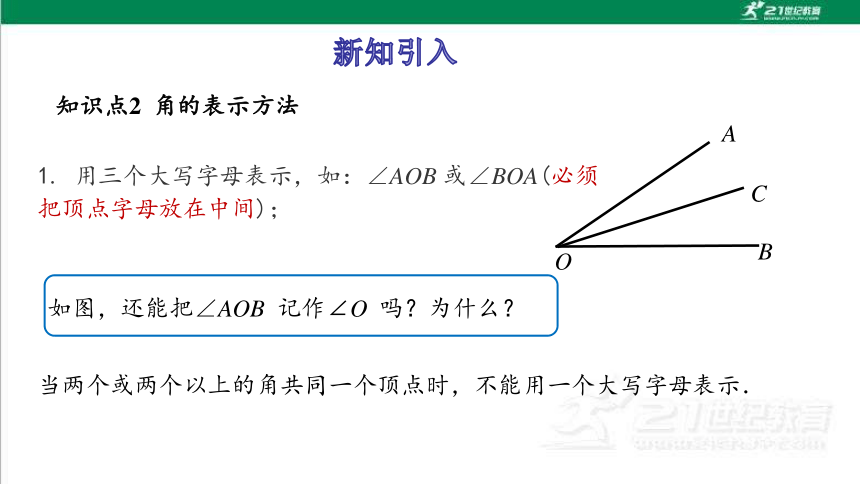
知识点2 角的表示方法
1. 用三个大写字母表示,如:∠AOB 或∠BOA(必须把顶点字母放在中间);
A
B
O
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示.
如图,还能把∠AOB 记作∠O 吗?为什么?
C
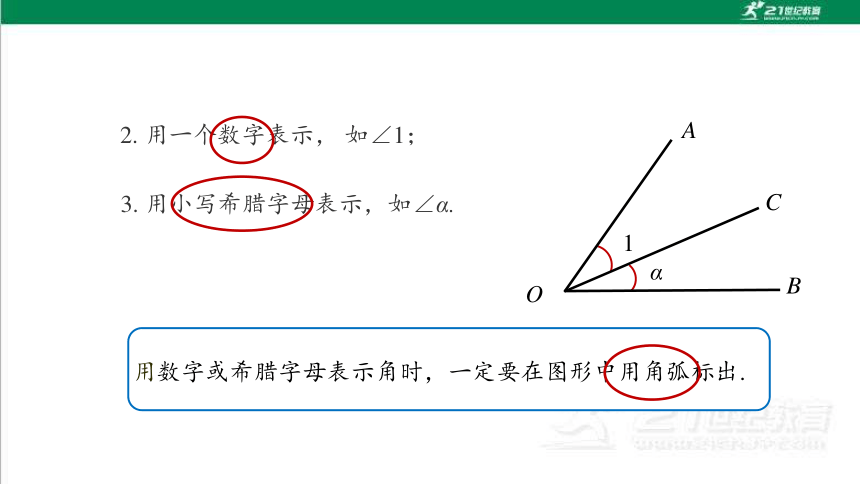
2. 用一个数字表示, 如∠1;
3. 用小写希腊字母表示,如∠α.
α
1
A
B
O
C
用数字或希腊字母表示角时,一定要在图形中用角弧标出.
注意:1. 角的符号应书写标准,“∠”不可与“<”混淆.
2. 当以某一点为顶点的角有两个或两个以上时,其中任何一个角都不能用一个顶点字母表示.
3. 如无特殊说明,在初中阶段所说的角一般都指小于平角的角.
例 如图,写出符合以下条件的角:
(1)能用一个大写字母表示的角;
(2)以A为顶点的角;
(3)小于平角的角.
导引:用一个大写字母表示的角不能有其他角与它共用顶点.
解:(1)∠B,∠C.
(2)∠BAC,∠BAD,∠CAD.
(3)∠BAC,∠B,∠C,∠1,∠2,∠3,∠4.
知识点3 角度制及换算
角的度量工具:量角器
怎么知道这个角的大小?
角的度量单位:
我们常用量角器量角,度、分、秒是常用的角的度量单位.
把一个周角 360等分,每一份就是 1 度的角,记作1°;
把 1 度的角 60 等分,每一份就是1 分的角,记作 1′;
把1分的角 60等分,每一份就是1 秒的角,记作1″.
如无特殊说明,初中阶段所说的角一般都指大于0 °且小于180 °的角.
1周角= °;1平角= °.
360
180
角度制:以度、分、秒为单位的角的度量制,叫作角度制.
注意:1.角的度量单位度、分、秒是60进制的,这和计量时间的单位时、分、秒的进制是一样的.
2.把高级单位转化为低级单位要乘进率;把低级单位转化为高级单位要除以进率.
3.转化时必须逐级进行,“越级”转化容易出错.
例1 度分秒的互化
⑴ 57.32 = ′ ″ ;
⑵ 17°6′36″= ° .
解析:57.32 =57 +0.32×60′
=57 +19.2′
=57 19′+0.2×60″
=57 19′12″
按1°=60′,1′=60″先把度化成分,再把分化成秒
(小数化整数)
最早明确使用角度制的文字记载于希腊学者托勒密(Ptolemaeus,约90-168)的《天文学大成》.托勒密在书中将圆周分为360等份,将1份记为1°,并采用古巴比伦的六十进制,定义出度、分、秒,这样便形成了角度制.
知识点4 方位角
八大方位:
正东:射线 OA
正南:射线 OB
正西:射线 OC
正北:射线 OD
西北方向:射线 OE
西南方向:射线 OF
东北方向:射线 OH
东南方向:射线 OG
E
H
F
G
B
东
西
北
南
A
D
C
O
45°
45°
45°
45°
如图,射线 OA 的方向是北偏东30°,射线 OB 的方向是南偏西60°,这里的“北偏东30°”和“南偏西60°”是用来表示方向的角,叫作方位角.
表示方向的角(方位角)在航行、测绘等工作中经常用到.
东北方向表示北偏东45°,
西北方向表示北偏西45°,
东南方向表示南偏东45°,
西南方向表示南偏西45°.
注意:方位角通常先写北或南,再写偏东或偏西,如“北偏东30°”一般不写成“东偏北60°”.
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
10°
45°
40°
60°
D
B
A
C
O
●
东
北
南
西
1.下列关于平角、周角的说法中,正确的是( )
①平角是一条直线
②周角是一条射线
③反向延长射线OA,就形成一个平角
④由一条射线绕其端点旋转,始边与终边重合而形成的图形叫周角
A.①③ B.②④ C.①④ D.③④
D
2.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A
3.如图,有下列说法:
①∠ECG和∠C是同一个角;
②∠OGF和∠OGB是同一个角;
③∠DOF和∠EOG是同一个角;
④∠ABC和∠ACB是同一个角.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
4.甲、乙、丙、丁,四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
A.甲说:“3时整和3时30分”
B.乙说:“6时15分和6时45分”
C.丙说:“9时整和12时15分”
D.丁说:“3时整和9时整”
D
5.如图,下列说法不正确的是( )
A.OC的方向是南偏东30°
B.OA的方向是北偏东45°
C.OB的方向是北偏西60°
D.∠AOB的度数是75°
D
6.魏老师到市场去买菜,发现若把5 kg的菜放到秤上,指针盘上的指针转了180°,如图所示.
(1)如果把0.5 kg的菜放在秤上,指针转过的角度是多少?
(2)如果指针转了270°,这些菜有多少千克?
1.下图中表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
2.下列说法正确的是( )
A.一条直线就是一个平角
B.一个角的两边画得越长,这个角就越大
C.反向延长射线OA就得到一个平角
D.画一条射线就得到周角
C
3.如图,钟表上10点整时,时针与分针所成的角是( )
A.30°
B.60°
C.90°
D.120°
4.若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论中正确的是( )
A.∠P=∠Q B.∠Q=∠R
C.∠P=∠R D.∠P=∠Q=∠R
B
C
5.如图,已知∠1:∠2:∠3=1:2:4,∠4=80°.求∠1,∠2,∠3的度数.
解:根据题意可设∠1=x°,∠2=2x°,∠3=4x°.
因为∠4=80°,
所以∠1+∠2+∠3=360°-80°,
即x+2x+4x=360-80,解得x=40.
所以∠1=40°,∠2=80°,∠3=160°.
角的定义
有公共端点的两条射线组成的图形
一条射线绕着它的端点旋转而形成的图形
角的表
示方法
用三个大写字母或一个大写字母表示
用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量
度、分、秒
角
1°=60′,1′=60″
方位角
通常要先写北或南,再写偏东或偏西
1. 理解角的定义和相关概念,掌握角的表示方法.
2. 会正确使用量角器测量角的大小.
3. 认识角的单位,会进行度、分、秒之间的换算.
4.认识方位角.
理解角的定义和相关概念,掌握角的表示方法.
认识角的单位,会进行度、分、秒之间的换算.
难点
重点
有公共端点的两条射线组成的图形叫作角.
这个公共端点是角的顶点.
这两条射线是角的两条边.
顶点
边
我们小学阶段已经学过角的概念,想一想小学阶段我们是怎样定义角的?
观察下面实物,你发现这些实物给我们共同的形象是什么?
知识点1 角的定义
角的动态定义:
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
始边
终边
O
A
B
O
A
B
(B)
平角
周角
如图,射线 OA 绕端点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
注意:1. 我们平时画角时,只画角的一部分,角的两边是
两条射线.
2. 角的大小只与构成角的两边张开的幅度有关.
3. 平角的两边成一条直线,但不能说平角就是直线;
周角两边重合形成一条射线,但不能说周角就是射线.
例1 下列说法中,正确的是( )
A.两条射线所组成的图形叫作角
B.有公共点的两条射线叫作角
C.一条射线绕着它的端点旋转叫作角
D.一条射线绕着它的端点旋转而形成的图形叫作角
D
例2 判断下列哪些图形是角
√
×
√
√
知识点2 角的表示方法
1. 用三个大写字母表示,如:∠AOB 或∠BOA(必须把顶点字母放在中间);
A
B
O
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示.
如图,还能把∠AOB 记作∠O 吗?为什么?
C
2. 用一个数字表示, 如∠1;
3. 用小写希腊字母表示,如∠α.
α
1
A
B
O
C
用数字或希腊字母表示角时,一定要在图形中用角弧标出.
注意:1. 角的符号应书写标准,“∠”不可与“<”混淆.
2. 当以某一点为顶点的角有两个或两个以上时,其中任何一个角都不能用一个顶点字母表示.
3. 如无特殊说明,在初中阶段所说的角一般都指小于平角的角.
例 如图,写出符合以下条件的角:
(1)能用一个大写字母表示的角;
(2)以A为顶点的角;
(3)小于平角的角.
导引:用一个大写字母表示的角不能有其他角与它共用顶点.
解:(1)∠B,∠C.
(2)∠BAC,∠BAD,∠CAD.
(3)∠BAC,∠B,∠C,∠1,∠2,∠3,∠4.
知识点3 角度制及换算
角的度量工具:量角器
怎么知道这个角的大小?
角的度量单位:
我们常用量角器量角,度、分、秒是常用的角的度量单位.
把一个周角 360等分,每一份就是 1 度的角,记作1°;
把 1 度的角 60 等分,每一份就是1 分的角,记作 1′;
把1分的角 60等分,每一份就是1 秒的角,记作1″.
如无特殊说明,初中阶段所说的角一般都指大于0 °且小于180 °的角.
1周角= °;1平角= °.
360
180
角度制:以度、分、秒为单位的角的度量制,叫作角度制.
注意:1.角的度量单位度、分、秒是60进制的,这和计量时间的单位时、分、秒的进制是一样的.
2.把高级单位转化为低级单位要乘进率;把低级单位转化为高级单位要除以进率.
3.转化时必须逐级进行,“越级”转化容易出错.
例1 度分秒的互化
⑴ 57.32 = ′ ″ ;
⑵ 17°6′36″= ° .
解析:57.32 =57 +0.32×60′
=57 +19.2′
=57 19′+0.2×60″
=57 19′12″
按1°=60′,1′=60″先把度化成分,再把分化成秒
(小数化整数)
最早明确使用角度制的文字记载于希腊学者托勒密(Ptolemaeus,约90-168)的《天文学大成》.托勒密在书中将圆周分为360等份,将1份记为1°,并采用古巴比伦的六十进制,定义出度、分、秒,这样便形成了角度制.
知识点4 方位角
八大方位:
正东:射线 OA
正南:射线 OB
正西:射线 OC
正北:射线 OD
西北方向:射线 OE
西南方向:射线 OF
东北方向:射线 OH
东南方向:射线 OG
E
H
F
G
B
东
西
北
南
A
D
C
O
45°
45°
45°
45°
如图,射线 OA 的方向是北偏东30°,射线 OB 的方向是南偏西60°,这里的“北偏东30°”和“南偏西60°”是用来表示方向的角,叫作方位角.
表示方向的角(方位角)在航行、测绘等工作中经常用到.
东北方向表示北偏东45°,
西北方向表示北偏西45°,
东南方向表示南偏东45°,
西南方向表示南偏西45°.
注意:方位角通常先写北或南,再写偏东或偏西,如“北偏东30°”一般不写成“东偏北60°”.
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
10°
45°
40°
60°
D
B
A
C
O
●
东
北
南
西
1.下列关于平角、周角的说法中,正确的是( )
①平角是一条直线
②周角是一条射线
③反向延长射线OA,就形成一个平角
④由一条射线绕其端点旋转,始边与终边重合而形成的图形叫周角
A.①③ B.②④ C.①④ D.③④
D
2.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A
3.如图,有下列说法:
①∠ECG和∠C是同一个角;
②∠OGF和∠OGB是同一个角;
③∠DOF和∠EOG是同一个角;
④∠ABC和∠ACB是同一个角.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
4.甲、乙、丙、丁,四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
A.甲说:“3时整和3时30分”
B.乙说:“6时15分和6时45分”
C.丙说:“9时整和12时15分”
D.丁说:“3时整和9时整”
D
5.如图,下列说法不正确的是( )
A.OC的方向是南偏东30°
B.OA的方向是北偏东45°
C.OB的方向是北偏西60°
D.∠AOB的度数是75°
D
6.魏老师到市场去买菜,发现若把5 kg的菜放到秤上,指针盘上的指针转了180°,如图所示.
(1)如果把0.5 kg的菜放在秤上,指针转过的角度是多少?
(2)如果指针转了270°,这些菜有多少千克?
1.下图中表示方法正确的有( )
A.1个 B.2个 C.3个 D.4个
B
2.下列说法正确的是( )
A.一条直线就是一个平角
B.一个角的两边画得越长,这个角就越大
C.反向延长射线OA就得到一个平角
D.画一条射线就得到周角
C
3.如图,钟表上10点整时,时针与分针所成的角是( )
A.30°
B.60°
C.90°
D.120°
4.若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论中正确的是( )
A.∠P=∠Q B.∠Q=∠R
C.∠P=∠R D.∠P=∠Q=∠R
B
C
5.如图,已知∠1:∠2:∠3=1:2:4,∠4=80°.求∠1,∠2,∠3的度数.
解:根据题意可设∠1=x°,∠2=2x°,∠3=4x°.
因为∠4=80°,
所以∠1+∠2+∠3=360°-80°,
即x+2x+4x=360-80,解得x=40.
所以∠1=40°,∠2=80°,∠3=160°.
角的定义
有公共端点的两条射线组成的图形
一条射线绕着它的端点旋转而形成的图形
角的表
示方法
用三个大写字母或一个大写字母表示
用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量
度、分、秒
角
1°=60′,1′=60″
方位角
通常要先写北或南,再写偏东或偏西
同课章节目录
