浙江省温州市2024-2025学年八年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 浙江省温州市2024-2025学年八年级(下)期末数学试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 118.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 00:00:00 | ||
图片预览



文档简介
浙江省温州市2024-2025学年八年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个人工智能的图标中,属于中心对称图形的是( )
A. B. C. D.
2.若二次根式有意义,则的取值范围是( )
A. B. C. D.
3.甲、乙两名运动员进行射击训练,每人射击次,若甲的方差单位:环为,乙比甲更稳定,则乙的方差可能是( )
A. B. C. D.
4.如图,在菱形中,,交于点若,,则的长为( )
A.
B.
C.
D.
5.用反证法证明命题“在中,如果,那么”时,应假设( )
A. B. C. D.
6.若点,都在反比例函数的图象上,则下列判断正确的是( )
A. B. C. D.
7.若算式的结果是有理数,则表示的运算符号是( )
A. B. C. D.
8.温州市年国内生产总值约为亿元,年约为亿元设这两年温州市的平均增长率为,则可列出方程( )
A. B.
C. D.
9.王老师设计了接力游戏:每人只能看到前一人的方程,并继续进行变形,将结果传递给下一人,最终求出方程的解,过程如图所示.
上述求解过程中,错误的是( )
A. 甲 B. 乙 C. 丙 D. 丁
10.如图,点,在线段上,射线,连结,以,为邻边作 ,连结,,记的长为,的长为若,,,则在点的运动过程中,下列代数式的值不变的是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.______.
12.在 中,,则 ______
13.小马同学在解方程时,等号左边的一个数字不小心被墨水污染了,如右式:已知一个根,则另一个根______.
14.每年月日是世界读书日,某校为了解学生周末课外阅读情况,随机抽取了名学生,得到统计图如图所示,则该名学生周末课外阅读时间的众数为______小时.
15.如图,矩形的顶点,在轴正半轴上,为的中点,反比例函数为常数,的图象经过点,交于点若与的面积之和为,则的值为______.
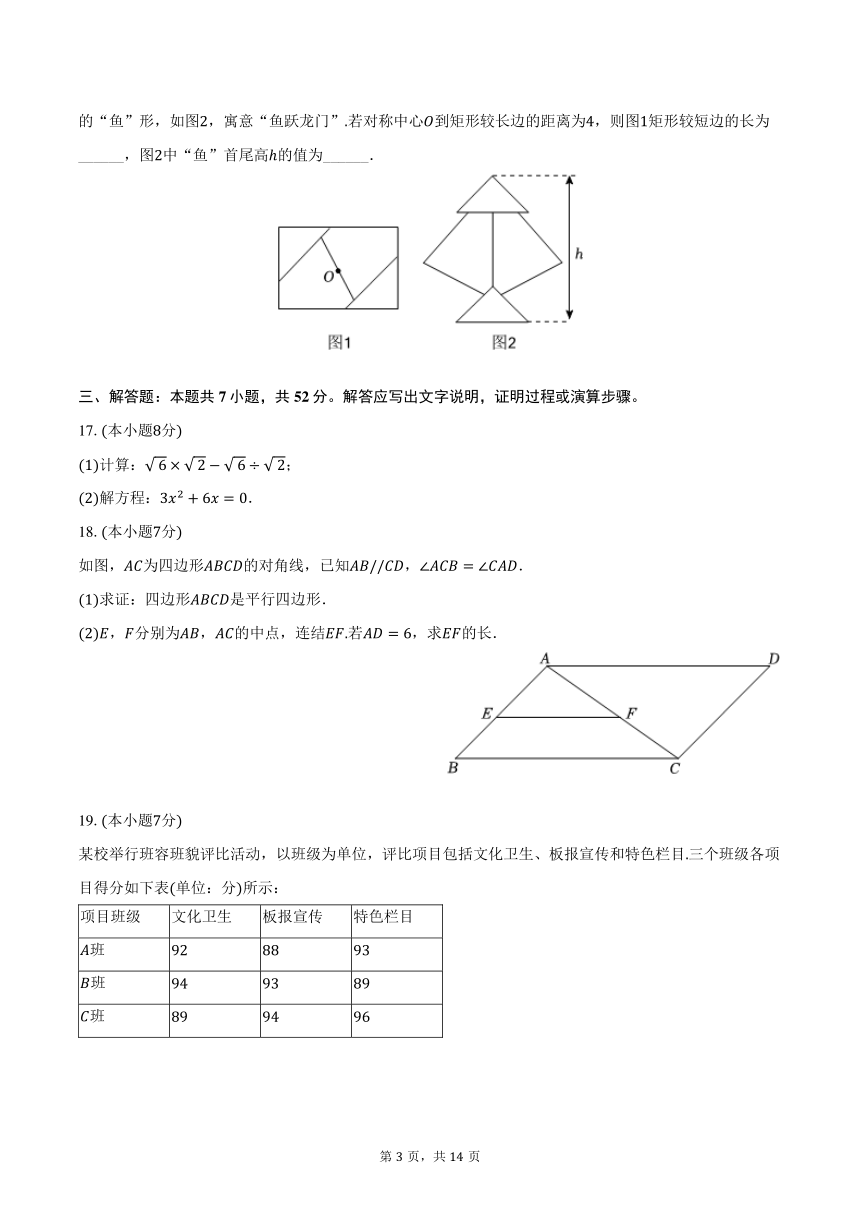
16.将一个相邻两边之比为:的矩形分成四部分,其中有两个全等的等腰直角三角形,其腰长与矩形较长边之比为:,如图,它是一个中心对称图形现拼成不重叠、无缝隙的轴对称的“鱼”形,如图,寓意“鱼跃龙门”若对称中心到矩形较长边的距离为,则图矩形较短边的长为______,图中“鱼”首尾高的值为______.
三、解答题:本题共7小题,共52分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:;
解方程:.
18.本小题分
如图,为四边形的对角线,已知,.
求证:四边形是平行四边形.
,分别为,的中点,连结若,求的长.
19.本小题分
某校举行班容班貌评比活动,以班级为单位,评比项目包括文化卫生、板报宣传和特色栏目三个班级各项目得分如下表单位:分所示:
项目班级 文化卫生 板报宣传 特色栏目
班
班
班
已知,两班的平均分分别是分、分,通过计算指出哪个班级平均分最高.
若将文化卫生、板报宣传和特色栏目的得分按::的比例计算总成绩,此时,班的总成绩分别为分和分,求班的总成绩,并根据总成绩从高到低给出班级排名.
20.本小题分
尺规作图:在矩形中,要求用直尺和圆规作菱形,使点,分别在边,上.
小明:如图,作的中垂线分别交,于点,,连结,.
小刚:如图,连结,作的中垂线分别交,于点,,连结,.
请选择一位同学的作法,判断是否正确,并说明理由注:若全选,按第一种作答评分
21.本小题分
已知一元二次方程.
若方程的一个根为,求的值.
当时,求证:方程有两个实数根.
22.本小题分
综合与实践:探索机器狗的速度问题.
素材:图是某款机器狗,它的最快速度米秒与总质量千克包括所载物体的质量的部分数据如下表,在直角坐标系中画出对应点,并用光滑曲线连起来图.
总质量千克
最快速度米秒
素材:机器狗自身质量为千克,实验室距离试验点米,机器狗需从试验点出发,送千克设备到实验室,卸下设备后马上原路返回装卸设备时间忽略不计
经探究发现是的正比例函数、一次函数、反比例函数中的一种.
任务:判断是的哪种函数类型,并求出该函数表达式.
任务:求机器狗所用的最短时间.
23.本小题分
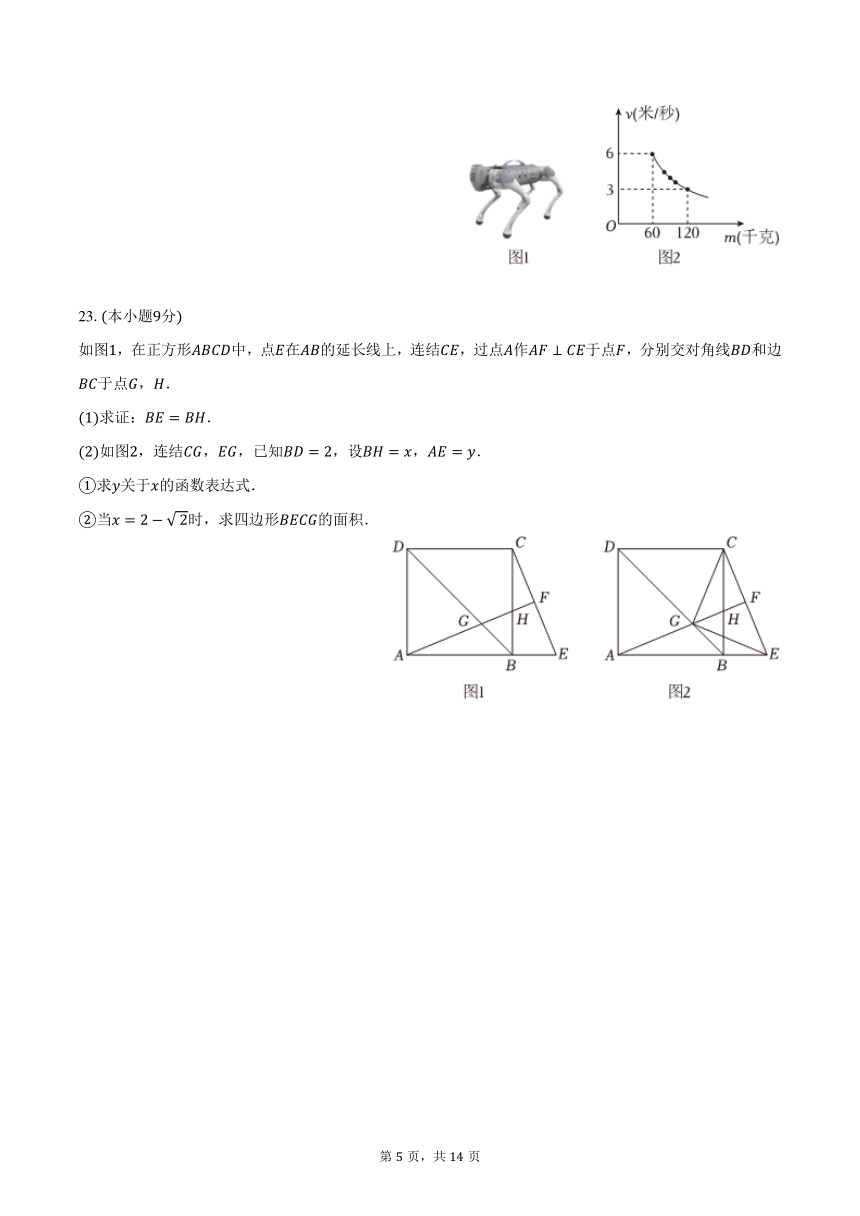
如图,在正方形中,点在的延长线上,连结,过点作于点,分别交对角线和边于点,.
求证:.
如图,连结,,已知,设,.
求关于的函数表达式.
当时,求四边形的面积.
答案和解析
1.【答案】
【解析】选项A、、的图形不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形;
选项B的图形能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形.
故选:.
2.【答案】
【解析】二次根式有意义,
,即,
则的范围是,
故选:.
3.【答案】
【解析】甲的方差为,乙比甲更稳定,
乙的方差小于,
故选:.
4.【答案】
【解析】四边形是菱形,
,,
,
,
,
故选:.
5.【答案】
【解析】反证法证明“在中,如果,那么”时,应假设,
故选:.
6.【答案】
【解析】反比例函数的,
反比例函数的图象分布在第一三象限,在每个象限内随的增大而减小,
,
.
故选:.
7.【答案】
【解析】、,结果不是有理数,故此选项不符合题意;
B、,结果不是有理数,故此选项不符合题意;
C、,结果不是有理数,故此选项不符合题意;
D、,结果是有理数,故此选项符合题意;
故选:.
8.【答案】
【解析】依题意得:.
故选:.
9.【答案】
【解析】,
,
则,即,
,
,,
错误的是乙,
故选:.
10.【答案】
【解析】点,在线段上,,
,
,,,
,
,
,
四边形是平行四边形,
,,,
,,
四边形是平行四边形,
,
,
,
,
代数式的值不变,
故选:.
11.【答案】
【解析】,
故答案为:.
12.【答案】
【解析】在 中,,
若,
则,
故答案为:.
13.【答案】
【解析】一元二次方程已知一个根是,
将代入中,得,解得,
解一元二次方程,得或,
方程的另一个根为,
故答案为:.
14.【答案】
【解析】数据出现了次,且次数最多,
所以众数是小时.
故答案为:.
15.【答案】
【解析】如图,延长交轴于点,
是矩形,且与的面积之和为,
,
为的中点,
,
反比例函数图象经过点,
,
故答案为:.
16.【答案】
【解析】过点作直线垂直矩形长边,交点为、,如图所示:
对称中心到矩形较长边的距离为,
图矩形较短边的长为;
即矩形的短边长为,
矩形相邻两边之比为:,
矩形的长边长为,
等腰直角三角形的腰长与矩形较长边之比为:,
等腰直角三角形的腰长为,
过点作,
如图所示:
,
由等腰直角三角形性质可得,
在等腰中,
,
由勾股定理得到斜边长为,
则,
图中“鱼”首尾高的值为,
故答案为:.
17.【答案】;
,.
【解析】原式
;
,
,
或,
,.
18.【解析】证明:,
,
,
四边形是平行四边形.
由可知,四边形是平行四边形,
,
,分别为,的中点,
是的中位线,
,
即的长为.
19.【解析】班的平均分为分,
,
班级平均分最高;
班总成绩为分,
,
班第,班第,班第.
20.【解析】选择小刚的作法,作法正确.
理由:设直线交于点,
直线为线段的垂直平分线,
,,.
四边形为矩形,
,
,,
≌,
,
,
四边形为菱形.
故小刚的作法正确.
选择小明的作法,作法不正确.
理由:直线为线段的垂直平分线,
,,
四边形为矩形,
,,
四边形为矩形,
,
,
四边形为平行四边形.
21.【解析】知一元二次方程一个根为,
,
,
,
;
,
,
,
方程有两个实数根.
22.【解析】任务:根据表格,,
是的反比例函数,该函数表达式为.
任务:当时,,
秒,
当时,,
秒,
秒,
机器狗所用的最短时间为秒.
23.证明:如图,四边形是正方形,
,,
,
,
,
,
≌,
;
如图,四边形是正方形,
,,,
,
,
,
;
如图,连接交于点,
四边形是正方形,
,,,
当时,,
,
,
,
,,
,
,
四边形的面积.
第5页,共14页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个人工智能的图标中,属于中心对称图形的是( )
A. B. C. D.
2.若二次根式有意义,则的取值范围是( )
A. B. C. D.
3.甲、乙两名运动员进行射击训练,每人射击次,若甲的方差单位:环为,乙比甲更稳定,则乙的方差可能是( )
A. B. C. D.
4.如图,在菱形中,,交于点若,,则的长为( )
A.
B.
C.
D.
5.用反证法证明命题“在中,如果,那么”时,应假设( )
A. B. C. D.
6.若点,都在反比例函数的图象上,则下列判断正确的是( )
A. B. C. D.
7.若算式的结果是有理数,则表示的运算符号是( )
A. B. C. D.
8.温州市年国内生产总值约为亿元,年约为亿元设这两年温州市的平均增长率为,则可列出方程( )
A. B.
C. D.
9.王老师设计了接力游戏:每人只能看到前一人的方程,并继续进行变形,将结果传递给下一人,最终求出方程的解,过程如图所示.
上述求解过程中,错误的是( )
A. 甲 B. 乙 C. 丙 D. 丁
10.如图,点,在线段上,射线,连结,以,为邻边作 ,连结,,记的长为,的长为若,,,则在点的运动过程中,下列代数式的值不变的是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.______.
12.在 中,,则 ______
13.小马同学在解方程时,等号左边的一个数字不小心被墨水污染了,如右式:已知一个根,则另一个根______.
14.每年月日是世界读书日,某校为了解学生周末课外阅读情况,随机抽取了名学生,得到统计图如图所示,则该名学生周末课外阅读时间的众数为______小时.
15.如图,矩形的顶点,在轴正半轴上,为的中点,反比例函数为常数,的图象经过点,交于点若与的面积之和为,则的值为______.
16.将一个相邻两边之比为:的矩形分成四部分,其中有两个全等的等腰直角三角形,其腰长与矩形较长边之比为:,如图,它是一个中心对称图形现拼成不重叠、无缝隙的轴对称的“鱼”形,如图,寓意“鱼跃龙门”若对称中心到矩形较长边的距离为,则图矩形较短边的长为______,图中“鱼”首尾高的值为______.
三、解答题:本题共7小题,共52分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:;
解方程:.
18.本小题分
如图,为四边形的对角线,已知,.
求证:四边形是平行四边形.
,分别为,的中点,连结若,求的长.
19.本小题分
某校举行班容班貌评比活动,以班级为单位,评比项目包括文化卫生、板报宣传和特色栏目三个班级各项目得分如下表单位:分所示:
项目班级 文化卫生 板报宣传 特色栏目
班
班
班
已知,两班的平均分分别是分、分,通过计算指出哪个班级平均分最高.
若将文化卫生、板报宣传和特色栏目的得分按::的比例计算总成绩,此时,班的总成绩分别为分和分,求班的总成绩,并根据总成绩从高到低给出班级排名.
20.本小题分
尺规作图:在矩形中,要求用直尺和圆规作菱形,使点,分别在边,上.
小明:如图,作的中垂线分别交,于点,,连结,.
小刚:如图,连结,作的中垂线分别交,于点,,连结,.
请选择一位同学的作法,判断是否正确,并说明理由注:若全选,按第一种作答评分
21.本小题分
已知一元二次方程.
若方程的一个根为,求的值.
当时,求证:方程有两个实数根.
22.本小题分
综合与实践:探索机器狗的速度问题.
素材:图是某款机器狗,它的最快速度米秒与总质量千克包括所载物体的质量的部分数据如下表,在直角坐标系中画出对应点,并用光滑曲线连起来图.
总质量千克
最快速度米秒
素材:机器狗自身质量为千克,实验室距离试验点米,机器狗需从试验点出发,送千克设备到实验室,卸下设备后马上原路返回装卸设备时间忽略不计
经探究发现是的正比例函数、一次函数、反比例函数中的一种.
任务:判断是的哪种函数类型,并求出该函数表达式.
任务:求机器狗所用的最短时间.
23.本小题分
如图,在正方形中,点在的延长线上,连结,过点作于点,分别交对角线和边于点,.
求证:.
如图,连结,,已知,设,.
求关于的函数表达式.
当时,求四边形的面积.
答案和解析
1.【答案】
【解析】选项A、、的图形不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形;
选项B的图形能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形.
故选:.
2.【答案】
【解析】二次根式有意义,
,即,
则的范围是,
故选:.
3.【答案】
【解析】甲的方差为,乙比甲更稳定,
乙的方差小于,
故选:.
4.【答案】
【解析】四边形是菱形,
,,
,
,
,
故选:.
5.【答案】
【解析】反证法证明“在中,如果,那么”时,应假设,
故选:.
6.【答案】
【解析】反比例函数的,
反比例函数的图象分布在第一三象限,在每个象限内随的增大而减小,
,
.
故选:.
7.【答案】
【解析】、,结果不是有理数,故此选项不符合题意;
B、,结果不是有理数,故此选项不符合题意;
C、,结果不是有理数,故此选项不符合题意;
D、,结果是有理数,故此选项符合题意;
故选:.
8.【答案】
【解析】依题意得:.
故选:.
9.【答案】
【解析】,
,
则,即,
,
,,
错误的是乙,
故选:.
10.【答案】
【解析】点,在线段上,,
,
,,,
,
,
,
四边形是平行四边形,
,,,
,,
四边形是平行四边形,
,
,
,
,
代数式的值不变,
故选:.
11.【答案】
【解析】,
故答案为:.
12.【答案】
【解析】在 中,,
若,
则,
故答案为:.
13.【答案】
【解析】一元二次方程已知一个根是,
将代入中,得,解得,
解一元二次方程,得或,
方程的另一个根为,
故答案为:.
14.【答案】
【解析】数据出现了次,且次数最多,
所以众数是小时.
故答案为:.
15.【答案】
【解析】如图,延长交轴于点,
是矩形,且与的面积之和为,
,
为的中点,
,
反比例函数图象经过点,
,
故答案为:.
16.【答案】
【解析】过点作直线垂直矩形长边,交点为、,如图所示:
对称中心到矩形较长边的距离为,
图矩形较短边的长为;
即矩形的短边长为,
矩形相邻两边之比为:,
矩形的长边长为,
等腰直角三角形的腰长与矩形较长边之比为:,
等腰直角三角形的腰长为,
过点作,
如图所示:
,
由等腰直角三角形性质可得,
在等腰中,
,
由勾股定理得到斜边长为,
则,
图中“鱼”首尾高的值为,
故答案为:.
17.【答案】;
,.
【解析】原式
;
,
,
或,
,.
18.【解析】证明:,
,
,
四边形是平行四边形.
由可知,四边形是平行四边形,
,
,分别为,的中点,
是的中位线,
,
即的长为.
19.【解析】班的平均分为分,
,
班级平均分最高;
班总成绩为分,
,
班第,班第,班第.
20.【解析】选择小刚的作法,作法正确.
理由:设直线交于点,
直线为线段的垂直平分线,
,,.
四边形为矩形,
,
,,
≌,
,
,
四边形为菱形.
故小刚的作法正确.
选择小明的作法,作法不正确.
理由:直线为线段的垂直平分线,
,,
四边形为矩形,
,,
四边形为矩形,
,
,
四边形为平行四边形.
21.【解析】知一元二次方程一个根为,
,
,
,
;
,
,
,
方程有两个实数根.
22.【解析】任务:根据表格,,
是的反比例函数,该函数表达式为.
任务:当时,,
秒,
当时,,
秒,
秒,
机器狗所用的最短时间为秒.
23.证明:如图,四边形是正方形,
,,
,
,
,
,
≌,
;
如图,四边形是正方形,
,,,
,
,
,
;
如图,连接交于点,
四边形是正方形,
,,,
当时,,
,
,
,
,,
,
,
四边形的面积.
第5页,共14页
同课章节目录
