1.3正方形的性质与判定(预习衔接.含解析)-2025-2026学年九年级上册数学北师大版
文档属性
| 名称 | 1.3正方形的性质与判定(预习衔接.含解析)-2025-2026学年九年级上册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 495.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:55:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
新课预习衔接 正方形的性质与判定
一.选择题(共5小题)
1.(2024 市北区校级二模)如图,正方形ABCD的对角线相交于点O,点E在AB边上,点F在OD上,过点E作EG⊥BD,垂足为点G,若FE=FC,EF⊥CF,OF=3,则BE的长为( )
A.3 B. C. D.
2.(2024春 锡山区期中)已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.若,PB=10,下列结论:
①△APD≌△AEB;②∠AEB=135°;③;④S△APD+S△APB=33;⑤CD=11.其中正确结论的序号是( )
A.①②③④ B.①④⑤ C.①②④ D.③④⑤
3.(2024 沙坪坝区模拟)如图,正方形ABCD中,点E为边BA延长线上一点,点F在边BC上,且AE=CF,连接DF,EF.若∠FDC=α.则∠AEF=( )
A.90°﹣2α B.45°﹣α C.45°+α D.α
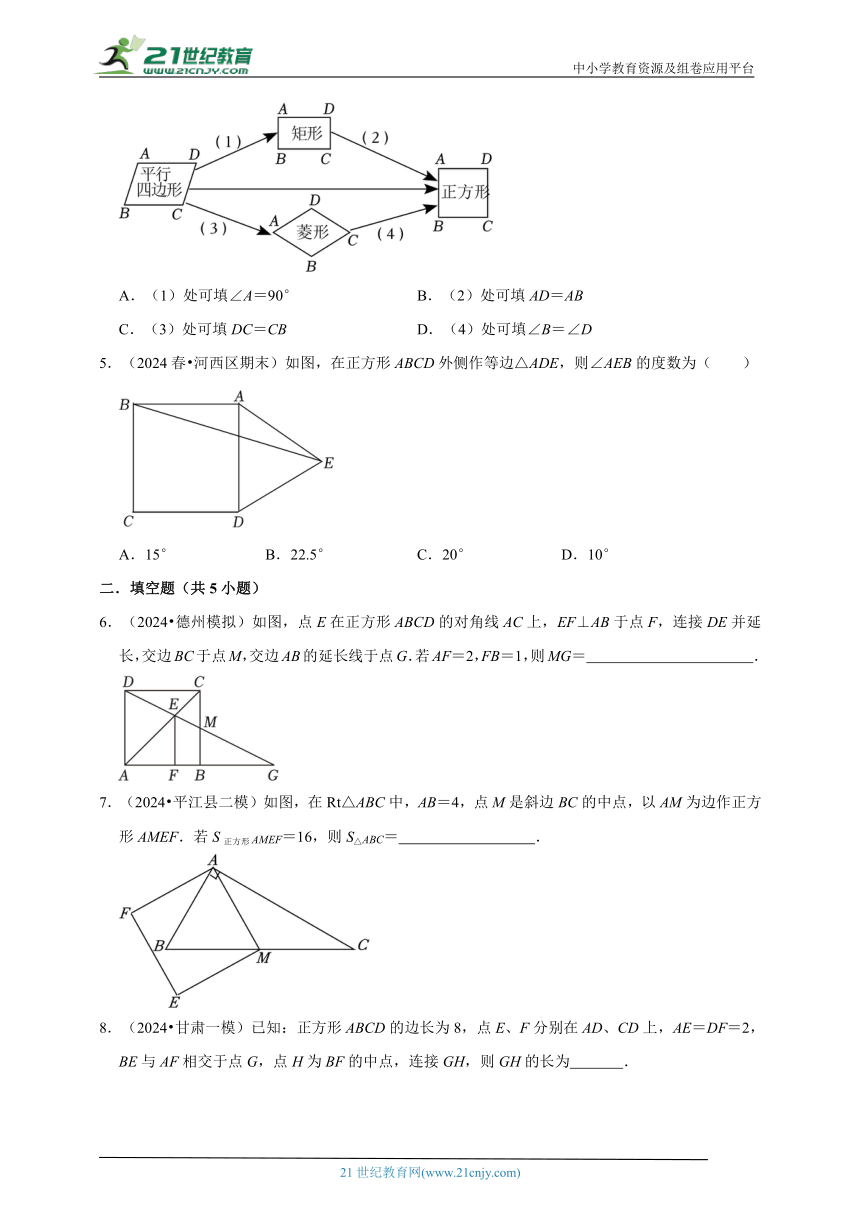
4.(2024春 任泽区期末)小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是( )
A.(1)处可填∠A=90° B.(2)处可填AD=AB
C.(3)处可填DC=CB D.(4)处可填∠B=∠D
5.(2024春 河西区期末)如图,在正方形ABCD外侧作等边△ADE,则∠AEB的度数为( )
A.15° B.22.5° C.20° D.10°
二.填空题(共5小题)
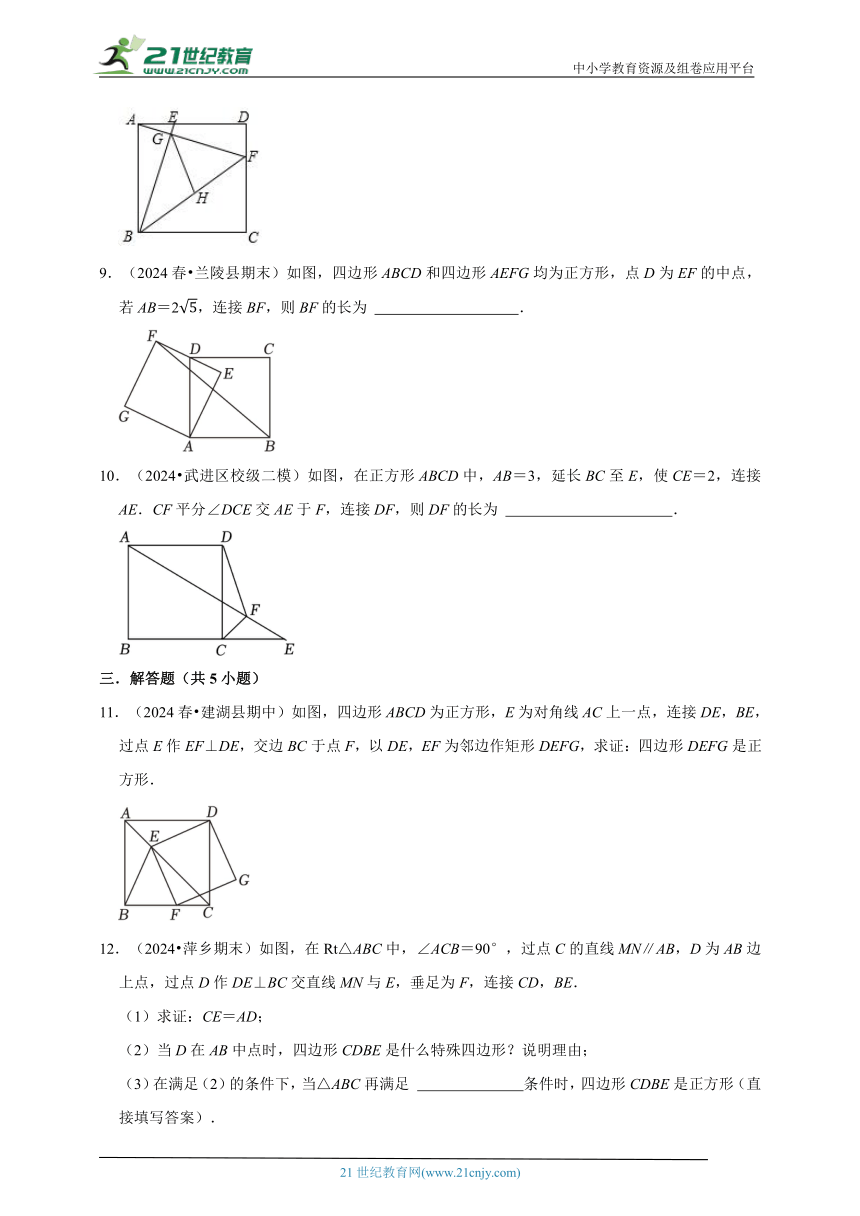
6.(2024 德州模拟)如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点F,连接DE并延长,交边BC于点M,交边AB的延长线于点G.若AF=2,FB=1,则MG= .
7.(2024 平江县二模)如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC= .
8.(2024 甘肃一模)已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
9.(2024春 兰陵县期末)如图,四边形ABCD和四边形AEFG均为正方形,点D为EF的中点,若AB=2,连接BF,则BF的长为 .
10.(2024 武进区校级二模)如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 .
三.解答题(共5小题)
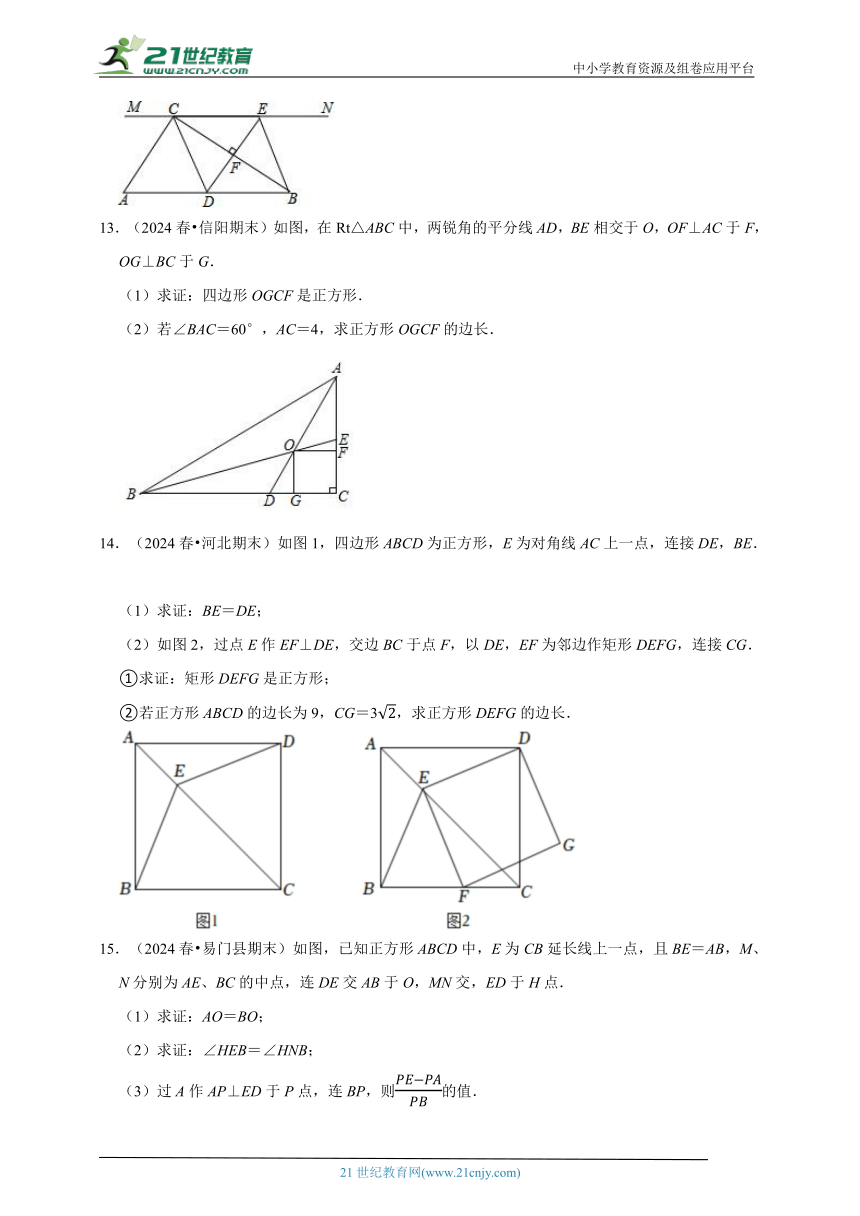
11.(2024春 建湖县期中)如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,求证:四边形DEFG是正方形.
12.(2024 萍乡期末)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上点,过点D作DE⊥BC交直线MN与E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形CDBE是什么特殊四边形?说明理由;
(3)在满足(2)的条件下,当△ABC再满足 条件时,四边形CDBE是正方形(直接填写答案).
13.(2024春 信阳期末)如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
14.(2024春 河北期末)如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
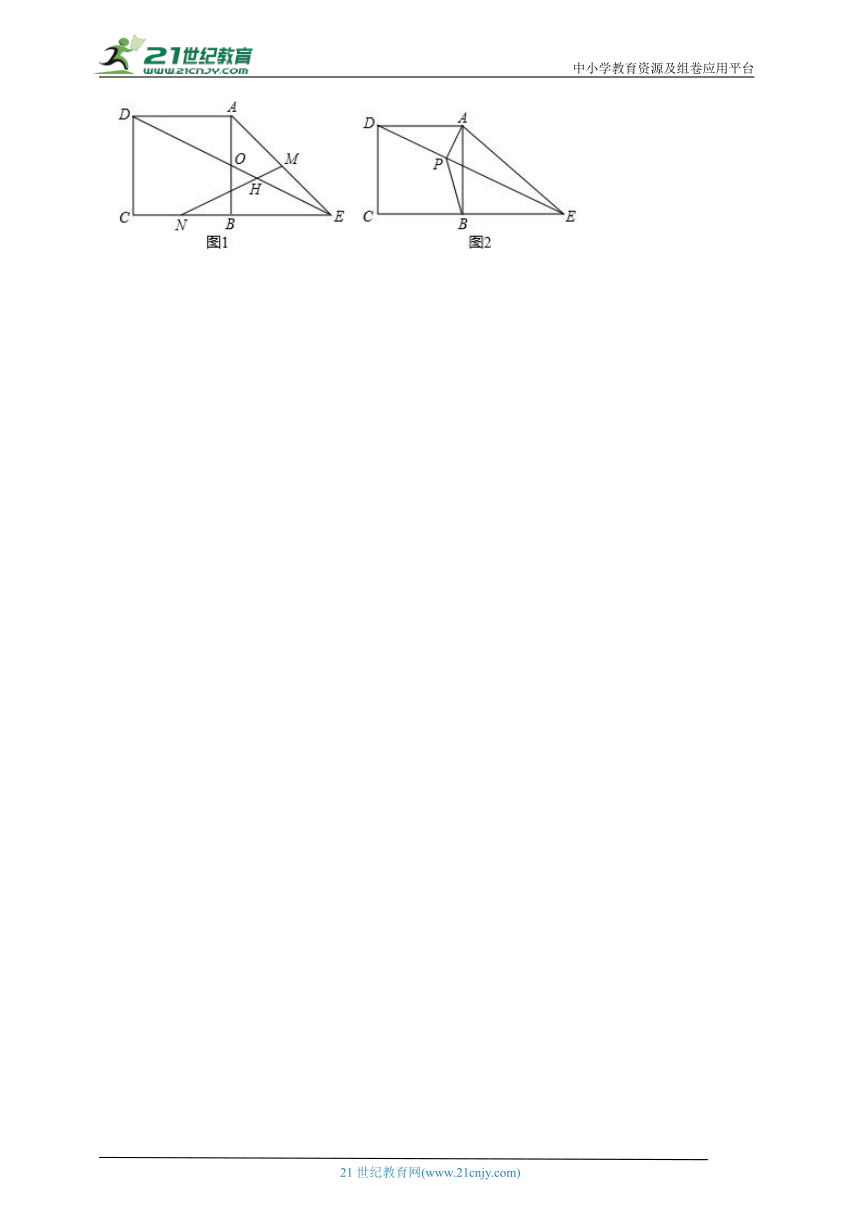
15.(2024春 易门县期末)如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
新课预习衔接 正方形的性质与判定
参考答案与试题解析
一.选择题(共5小题)
1.(2024 市北区校级二模)如图,正方形ABCD的对角线相交于点O,点E在AB边上,点F在OD上,过点E作EG⊥BD,垂足为点G,若FE=FC,EF⊥CF,OF=3,则BE的长为( )
A.3 B. C. D.
【考点】正方形的性质;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【答案】B
【分析】证明△EFG≌△CFO(ASA),可得EG=OF=3,再利用等腰直角三角形即可解决问题.
【解答】解:∵四边形ABCD是正方形,
∴AC⊥BD,∠ABD=45°,
∵EF⊥CF,
∴∠COF=∠EFC=90°,
∴∠EFG=90°﹣∠CFO=∠FCO,
∵EG⊥BD,
∴∠EGF=∠FOC=90°,
在△EFG和△FCO中,
,
∴△EFG≌△FCO(AAS),
∴EG=OF=3,
∵∠ABD=45°,
∴△EBG是等腰直角三角形,
∴BEEG=3,
故选:B.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,解决本题的关键是得到△EFG≌△FCO.
2.(2024春 锡山区期中)已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.若,PB=10,下列结论:
①△APD≌△AEB;②∠AEB=135°;③;④S△APD+S△APB=33;⑤CD=11.其中正确结论的序号是( )
A.①②③④ B.①④⑤ C.①②④ D.③④⑤
【考点】正方形的性质;三角形的面积;全等三角形的判定与性质;等腰三角形的判定;勾股定理.
【专题】几何综合题;矩形 菱形 正方形;推理能力.
【答案】C
【分析】①利用SAS即可证明△APD≌△AEB,进而可以判断①正确;②根据△APD≌△AEB和等腰直角三角形的性质得出∠APE=∠AEP=45°,得出∠APD=∠AEB=135°,进而可以判断②正确;③根据勾股定理计算可得EB的长,进而可以判断③;④连接BD,可得S△APD+S△APB=S△AEP+S△EPB=33,即可判断④;⑤根据S△ABD=S△APD+S△APB+S△BPD=33+32=65,进而可以判断⑤.
【解答】解:①在正方形ABCD,AB=AD,∠BAD=90°,
∵EA⊥PA,
∴∠EAP=∠BAD=90°
∴∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
∵AE=AP,
在△APD和△AEB中,
,
∴△APD≌△AEB(SAS);故①成立;
②∵AE=AP=3,∠EAP=90°,
∴∠AEP=∠APE=45°,PEAE=6,
∵△APD≌△AEB,
∴∠AEB=∠APD=180°﹣45°=135°,故②成立;
③∴∠BEP=135°﹣45°=90°,
∴EB⊥ED,
在Rt△BPE中,PE=6,PB=10,
∴BE8,故③不成立;
④如图,连接BD,
由②得:PE=6,BE=8,
∵△APD≌△AEB,
∴S△APD+S△APB
=S△AEB+S△APB
=S四边形AEBP
=S△AEP+S△EPB
AE AP PE BE
336×8
=33.故④成立;
∵△APD≌△AEB,
∴PD=BE=8,
∴S△BDPPD BE=32,
∴S△ABD=S△APD+S△APB+S△BPD=33+32=65,
∴S正方形ABCD=2S△ABD=130,
∴CD2=130,
∴CD,故⑤不成立.
综上所述,正确结论的序号是①②④,
故选:C.
【点评】本题考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等是解题的关键.
3.(2024 沙坪坝区模拟)如图,正方形ABCD中,点E为边BA延长线上一点,点F在边BC上,且AE=CF,连接DF,EF.若∠FDC=α.则∠AEF=( )
A.90°﹣2α B.45°﹣α C.45°+α D.α
【考点】正方形的性质;全等三角形的判定与性质.
【专题】矩形 菱形 正方形;运算能力.
【答案】B
【分析】连接ED,根据正方形的性质可得∠ADC=∠BAD=∠C=90°,AD=DC,再由全等三角形的判定与性质可得∠FDC=∠ADE=α,最后由等腰直角三角形的性质及三角形外角性质可得答案.
【解答】解:连接ED,
在正方形ABCD中,∠ADC=∠BAD=∠C=90°,AD=DC,
∵AE=CF,
∴Rt△ADE≌Rt△CDF(SAS),
∴∠FDC=∠ADE=α,DE=DF,
∴∠CDF+∠ADF=∠ADE+∠ADF=90°,
∴∠EFD=∠FED=45°,
∴∠AGE=∠FED+∠ADE=45°+α,
∴∠AEF=90°﹣∠AGE=90°﹣(45°+α)=45°﹣α,
故选:B.
【点评】此题考查的是正方形的性质、全等三角形的判定与性质,正确作出辅助线是解决此题的关键.
4.(2024春 任泽区期末)小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是( )
A.(1)处可填∠A=90° B.(2)处可填AD=AB
C.(3)处可填DC=CB D.(4)处可填∠B=∠D
【考点】正方形的判定;菱形的判定;矩形的判定.
【专题】矩形 菱形 正方形;推理能力.
【答案】D
【分析】根据正方形、矩形、菱形的判定定理判断即可.
【解答】解:A、有一个角是直角的平行四边形是矩形,
∴(1)处可填∠A=90°是正确的,故该选项不符合题意;
B、一组邻边相等的矩形是正方形,
∴(2)处可填AD=AB是正确的,故该选项不符合题意;
C、一组邻边相等的平行四边形是菱形,
∴(3)处可填DC=CB是正确的,故该选项不符合题意;
D、有一个角是直角的菱形是正方形,
∴∠B=∠D无法判定两角是不是直角,故该选项不符合题意;
故选:D.
【点评】本题主要考查了矩形的判定,正方形的判定和菱形的判定,熟练掌握特殊四边形的关系是解题的关键.
5.(2024春 河西区期末)如图,在正方形ABCD外侧作等边△ADE,则∠AEB的度数为( )
A.15° B.22.5° C.20° D.10°
【考点】正方形的性质;等边三角形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;几何直观.
【答案】A
【分析】由四边形ABCD是正方形,△ADE是正三角形可得AB=AE,利用正方形和正三角形的内角性质即可得答案.
【解答】解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
又∵△ADE是正三角形,
∴AE=AD,∠DAE=60°,
∴△ABE是等腰三角形,∠BAE=90°+60°=150°,
∴∠ABE=∠AEB=15°.
故选:A.
【点评】本题题主要考查了正方形和等边三角形的性质,同时也利用了三角形的内角和,解题首先利用正方形和等边三角形的性质证明等腰三角形,然后利用等腰三角形的性质即可解决问题.
二.填空题(共5小题)
6.(2024 德州模拟)如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点F,连接DE并延长,交边BC于点M,交边AB的延长线于点G.若AF=2,FB=1,则MG= .
【考点】正方形的性质.
【专题】图形的全等;矩形 菱形 正方形;图形的相似;推理能力.
【答案】.
【分析】由正方形性质得:BC=CD=AB=AF+FB=2+1=3,∠ABC=∠CBG=90°,DC∥AG,运用平行线成比例定理得,由DC∥AG,可得△CDE∽△AGE,求得AG=2CD=6,BG=3=CD,再证得△CDM≌△BGM(AAS),可得CM=BMBC,运用勾股定理即可求得答案.
【解答】解:∵四边形ABCD是正方形,AF=2,FB=1,
∴BC=CD=AB=AF+FB=2+1=3,∠ABC=∠CBG=90°,DC∥AG,
∵EF⊥AB,
∴∠AFE=90°,
∴∠AFE=∠ABC,
∴EF∥BC,
∴,
∵DC∥AG,
∴△CDE∽△AGE,
∴,
∴AG=2CD=6,
∴BG=AG﹣AB=6﹣3=3,
∴BG=CD,
∵CD∥AG,
∴∠CDM=∠G,
在△CDM和△BGM中,
,
∴△CDM≌△BGM(AAS),
∴CM=BMBC,
在Rt△BGM中,MG.
故答案为:.
【点评】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,平行线分线段成比例定理等,解题关键是熟练运用相似三角形的判定和性质.
7.(2024 平江县二模)如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC= .
【考点】正方形的性质;三角形的面积;直角三角形斜边上的中线.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;几何直观;运算能力;推理能力.
【答案】.
【分析】先根据正方形的面积公式求出AM=4,再根据直角三角形的性质得BC=2AM=8,进而利用勾股定理求出AC,然后根据直角三角形的面积公式可求出△ABC的面积.
【解答】解:∵四边形AMEF为正方形,
∴S正方形AMEF=AM2,
又∵S正方形AMEF=16,
∴AM2=16,
∴AM=4,
在Rt△ABC中,点M是斜边BC的中点,
∴BC=2AM=8,
在Rt△ABC中,BC=8,AB=4,
由勾股定理得:AC,
∴S△ABCAB AC4.
故答案为:.
【点评】此题主要考查了正方形的面积,直角三角形的面积,直角三角形的性质,熟练掌握正方形和直角三角形的面积公式,理解直角三角形斜边上的中线等于斜边的一半是解决问题的关键.
8.(2024 甘肃一模)已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 5 .
【考点】正方形的性质;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形.
【答案】见试题解答内容
【分析】根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GHBF,利用勾股定理求出BF的长即可得出答案.
【解答】解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
∵AB=AD,∠BAE=∠D,AE=DF
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GHBF,
∵BC=8,CF=CD﹣DF=8﹣2=6
∴BF10
∴GH=5
故答案为:5
【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形两锐角互余等知识,掌握三角形全等的判定方法与正方形的性质是解题的关键.
9.(2024春 兰陵县期末)如图,四边形ABCD和四边形AEFG均为正方形,点D为EF的中点,若AB=2,连接BF,则BF的长为 .
【考点】正方形的性质.
【专题】矩形 菱形 正方形;运算能力;推理能力.
【答案】.
【分析】连接AF,让△ADF绕点A顺时针旋转90°,此时AD与AB重合,得到△ABF′,连接EF′,根据旋转的性质得到△ADF≌△ABF′,再证明△AEF≌△AEF′,可得F,E,F′三点共线,根据三线合一得到FF′的值,最后利用角度的等量转换得到∠FF′B=90°,再根据勾股定理,即可解答.
【解答】解:如图,连接AF,让△ADF绕点A顺时针旋转90°,此时AD与AB重合,得到△ABF′,连接EF′,
∵四边形ABCD和四边形AEFG均为正方形,
∴EF=EA,∠FEA=90°,AD=AB,
根据旋转的性质,可得△ADF≌△ABF′,∠FAF′=90°,∠FAD=∠F′AB,
∴AF=AF′,∠AFE=∠AF′E=45°,
∴∠FAE=90°﹣∠AFF′=45°=∠DAF+∠DAE,
∴∠DAE+∠BAF′=45°,
∴∠EAF′=∠DAB﹣(∠DAE+∠BAF′)=45°,
∴△FAE≌△F′AE(SAS),
∴∠AEF=∠AEF′=90°,
可得F,E,F′三点共线,
∵∠AEF=90°,AF=AF′,
∴EF=EF′,
∵点D为EF的中点,
∴,
设ED=x,则AE=2x,
根据勾股定理可得,AE2+ED2=AD2,
即,
解得x=2(舍去负值),
∴EF=AE=4,BF′=DF=2,
∵AE⊥FF′,AF=AF′,
∴EF=EF′=4,
∴FF′=8,
∵∠EAF+∠AF′B=45°+45°=90°,
∴,
故答案为:.
【点评】本题考查了旋转的性质,全等三角形的性质,正方形的性质,等腰三角形的判定和性质,勾股定理,正确画出辅助线,耐心推理是解题的关键.
10.(2024 武进区校级二模)如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 .
【考点】正方形的性质;角平分线的性质.
【专题】矩形 菱形 正方形;图形的相似;运算能力;推理能力.
【答案】见试题解答内容
【分析】过点F作FM⊥CE于M,作FN⊥CD于点N,首先证四边形CMFN为正方形,再设CM=a,则FM=FN=CM=CN=a,BE=5,EM=2﹣a,然后证△EFM和△EAB相似,由相似三角形的性质求出a,进而在Rt△AFN中由勾股定理即可求出DF.
【解答】解:过点F作FM⊥CE于M,作FN⊥CD于点N,
∵四边形ABCD为正方形,AB=3,
∴∠ABC=90°,BC=AB=CD=3,AB∥CD,
∵FM⊥CE,FN⊥CD,∠DCE=∠B=90°,
∴四边形CMFN为矩形,
又∵CF平分∠DCE,FM⊥CE,FN⊥CD,
∴FM=FN,
∴四边形CMFN为正方形,
∴FM=FN=CM=CN,
设CM=a,则FM=FN=CM=CN=a,
∵CE=2,
∴BE=BC+CE=5,EM=CE﹣CM=2﹣a,
∵∠B=90°,FM⊥CE,
∴FM∥AB,
∴△EFM∽△EAB,
∴FM:AB=EM:BE,
即:a:3=(2﹣a):5,
解得:,
∴,
∴,
在Rt△DFN中,,,
由勾股定理得:.
故答案为:.
【点评】此题主要考查了正方形的判定及性质,相似三角形的判定和性质,勾股定理等,解答此题的关键是熟练掌握相似三角形的判定方法,理解相似三角形的对应边成比例.
三.解答题(共5小题)
11.(2024春 建湖县期中)如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,求证:四边形DEFG是正方形.
【考点】正方形的判定与性质;全等三角形的判定与性质;矩形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】见解析.
【分析】过点E分别作EM⊥BC于点M,EN⊥CD于点N,证明四边形EMCN为正方形,则EM=EN,∠MEN=90°,证明△DEN≌△FEM(ASA),得到ED=EF,即可得到结论.
【解答】证明:如图,过点E分别作EM⊥BC于点M,EN⊥CD于点N,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ECN=∠ECM=45°,
∴∠EMC=∠ENC=∠BCD=90°,
∴NE=NC,
∴四边形EMCN为正方形,
∴EM=EN,∠MEN=90°,
∵四边形DEFG是矩形,
∴∠DEF=90°,
∴∠DEN+∠NEF=∠FEM+∠NEF=90°,
∴∠DEN=∠FEM,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形.
【点评】此题考查了正方形的判定和性质、矩形的性质、全等三角形的判定和性质、角平分线的性质等知识,证明△DEN≌△FEM(ASA)是解题的关键.
12.(2024 萍乡期末)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上点,过点D作DE⊥BC交直线MN与E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形CDBE是什么特殊四边形?说明理由;
(3)在满足(2)的条件下,当△ABC再满足 等腰直角三角形 条件时,四边形CDBE是正方形(直接填写答案).
【考点】正方形的判定.
【专题】矩形 菱形 正方形;推理能力.
【答案】(1)见解析;
(2)四边形BECD是菱形,理由见解析;
(3)当△ABC是等腰直角三角形时,四边形BECD是正方形;理由见解析.
【分析】(1)证出AC∥DE,得出四边形ADEC是平行四边形,即可得出结论;
(2)先证出BD=CE,得出四边形BECD是平行四边形,再由直角三角形斜边上的中线性质得出CDAB=BD,即可得出四边形BECD是菱形;
(3)当△ABC是等腰直角三角形,由等腰三角形的性质得出CD⊥AB,即可得出四边形BECD是正方形.
【解答】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CDAB=BD,
∴四边形BECD是菱形;
(3)解:当△ABC是等腰直角三角形时,四边形BECD是正方形;理由如下:
∵∠ACB=90°,
当△ABC是等腰直角三角形,
∵D为AB的中点,
∴CD⊥AB,
∴∠CDB=90°,
∴四边形BECD是正方形,
故答案为:等腰直角三角形.
【点评】本题考查了平行四边形的判定与性质、正方形的判定、菱形的判定、直角三角形斜边上的中线性质;熟练掌握平行四边形的判定与性质,并能进行推理论证是解决问题的关键.
13.(2024春 信阳期末)如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
【考点】正方形的判定与性质;角平分线的性质;含30度角的直角三角形.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;几何直观;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)根据有三个角是直角的四边形是矩形,可得四边形OGCF是矩形,根据角平分线的性质,可得OH与OF,OH与OG的关系,根据邻边相等的矩形是正方形,可得答案;
(2)由含30°角的直角三角形的性质和勾股定理求出AB和BC,根据全等三角形判定的HL定理证得Rt△AOH≌Rt△AOF得到AH=AF,设正方形OGCF的边长为x,则AH=AF=4﹣x,BH=BG=4x,根据AB=AH+BH=8,解方程即可求出x.
【解答】(1)证明:过O作OH⊥AB于H点,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的角平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF,
又四边形OGCF是矩形,
∴四边形OGCF是正方形;
(2)解:在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=90°﹣60°=30°,
∴ACAB,
∵AC=4,
∴AB=2AC=2×4=8,
∵AC2+BC2=AB2,
∴BC4,
在Rt△AOH和Rt△AOF中,
,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF的边长为x,
则AH=AF=4﹣x,BH=BG=4x,
∴4﹣x+4x=8,
∴x=22,
即正方形OGCF的边长为22.
【点评】本题主要考查了正方形的判定和性质,角平分线的性质,全等三角形的判定和性质,含30°角的直角三角形的性质和勾股定理,正确作出辅助线,且根据角平分线的性质推出OH=OF=OG是解决问题的关键.
14.(2024春 河北期末)如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
【考点】正方形的判定与性质;全等三角形的判定与性质;矩形的性质.
【专题】证明题;矩形 菱形 正方形;推理能力.
【答案】(1)证明过程见解答;
(2)①证明过程见解答;
②3.
【分析】(1)根据正方形的性质证明△ABE≌△ADE(SAS),即可解决问题;
(2)①作EM⊥BC于M,EN⊥CD于N,得到EN=EM,然后证得∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF,根据正方形的判定即可证得矩形DEFG是正方形;
②证明△ADE≌△CDG(SAS),可得AE=CG,∠DAE=∠DCG=45°,证明CE⊥CG,连接EG,根据勾股定理即可解决问题.
【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
【点评】此题主要考查了正方形的判定与性质,矩形的性质,三角形的全等的性质和判定,勾股定理,解本题的关键是正确作出辅助线,证得△DEN≌△FEM.
15.(2024春 易门县期末)如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
【考点】正方形的性质;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【答案】(1)见解析;
(2)见解析;
(3).
【分析】(1)根据正方形的性质得到AD=AB,AD∥BC,根据全等三角形的性质即可得到结论;
(2)延长BC至F,且使CF=BC,连接AF,则BM=CE,由SAS证明△ABF≌△DCE,得出∠DEC=∠AFB,证出MN为△AEF的中位线,得出MN∥AF,得出∠HNE=∠AFB=∠HEN,即可得出HE=HN;
(3)过点B作BQ⊥BP交DE于Q,由ASA证明△BEQ≌△BAP,得出PA=QE,QB=PB,证出△PBQ是等腰直角三角形,由勾股定理得出PQPB,即可得出答案;
【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,AD∥BC,
∴∠DAB=∠ABE,∠ADO=∠BEO,
∵AB=BE,
∴AD=BE,
∴△ADO≌△BEO(ASA),
∴AO=BO;
(2)证明:延长BC至F,且使CF=BC,连接AF,如图1所示:
则BF=CE,
∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=∠ABC=∠DCB=90°,
在△ABF和△DCE中,,
∴△ABF≌△DCE(SAS),
∴∠DEC=∠AFB,
∵EB=CF,BN=CN,
∴N为EF的中点,
∴MN为△AEF的中位线,
∴MN∥AF,
∴∠HNB=∠AFB=∠HEB;
(3)解:过点B作BQ⊥BP交DE于Q,如图2所示:
则∠PBQ=90°,
∵∠ABE=180°﹣∠ABC=90°,
∴∠EBQ=∠ABP,
∵AD∥BC,
∴∠ADP=∠BEQ,
∵AP⊥DE,∠BAD=90°,
由角的互余关系得:∠BAP=∠ADP,
∴∠BEQ=∠BAP,
在△BEQ和△BAP中,,
∴△BEQ≌△BAP(ASA),
∴PA=QE,QB=PB,
∴△PBQ是等腰直角三角形,
∴PQPB,
∴.
【点评】本题考查了正方形的性质、全等三角形的判定与性质、平行线的性质、等腰直角三角形的判定与性质、勾股定理、直角三角形的性质等知识;本题综合性强,有一定难度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 正方形的性质与判定
一.选择题(共5小题)
1.(2024 市北区校级二模)如图,正方形ABCD的对角线相交于点O,点E在AB边上,点F在OD上,过点E作EG⊥BD,垂足为点G,若FE=FC,EF⊥CF,OF=3,则BE的长为( )
A.3 B. C. D.
2.(2024春 锡山区期中)已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.若,PB=10,下列结论:
①△APD≌△AEB;②∠AEB=135°;③;④S△APD+S△APB=33;⑤CD=11.其中正确结论的序号是( )
A.①②③④ B.①④⑤ C.①②④ D.③④⑤
3.(2024 沙坪坝区模拟)如图,正方形ABCD中,点E为边BA延长线上一点,点F在边BC上,且AE=CF,连接DF,EF.若∠FDC=α.则∠AEF=( )
A.90°﹣2α B.45°﹣α C.45°+α D.α
4.(2024春 任泽区期末)小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是( )
A.(1)处可填∠A=90° B.(2)处可填AD=AB
C.(3)处可填DC=CB D.(4)处可填∠B=∠D
5.(2024春 河西区期末)如图,在正方形ABCD外侧作等边△ADE,则∠AEB的度数为( )
A.15° B.22.5° C.20° D.10°
二.填空题(共5小题)
6.(2024 德州模拟)如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点F,连接DE并延长,交边BC于点M,交边AB的延长线于点G.若AF=2,FB=1,则MG= .
7.(2024 平江县二模)如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC= .
8.(2024 甘肃一模)已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
9.(2024春 兰陵县期末)如图,四边形ABCD和四边形AEFG均为正方形,点D为EF的中点,若AB=2,连接BF,则BF的长为 .
10.(2024 武进区校级二模)如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 .
三.解答题(共5小题)
11.(2024春 建湖县期中)如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,求证:四边形DEFG是正方形.
12.(2024 萍乡期末)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上点,过点D作DE⊥BC交直线MN与E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形CDBE是什么特殊四边形?说明理由;
(3)在满足(2)的条件下,当△ABC再满足 条件时,四边形CDBE是正方形(直接填写答案).
13.(2024春 信阳期末)如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
14.(2024春 河北期末)如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
15.(2024春 易门县期末)如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
新课预习衔接 正方形的性质与判定
参考答案与试题解析
一.选择题(共5小题)
1.(2024 市北区校级二模)如图,正方形ABCD的对角线相交于点O,点E在AB边上,点F在OD上,过点E作EG⊥BD,垂足为点G,若FE=FC,EF⊥CF,OF=3,则BE的长为( )
A.3 B. C. D.
【考点】正方形的性质;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【答案】B
【分析】证明△EFG≌△CFO(ASA),可得EG=OF=3,再利用等腰直角三角形即可解决问题.
【解答】解:∵四边形ABCD是正方形,
∴AC⊥BD,∠ABD=45°,
∵EF⊥CF,
∴∠COF=∠EFC=90°,
∴∠EFG=90°﹣∠CFO=∠FCO,
∵EG⊥BD,
∴∠EGF=∠FOC=90°,
在△EFG和△FCO中,
,
∴△EFG≌△FCO(AAS),
∴EG=OF=3,
∵∠ABD=45°,
∴△EBG是等腰直角三角形,
∴BEEG=3,
故选:B.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,解决本题的关键是得到△EFG≌△FCO.
2.(2024春 锡山区期中)已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE.过点A作AE的垂线交DE于点P.若,PB=10,下列结论:
①△APD≌△AEB;②∠AEB=135°;③;④S△APD+S△APB=33;⑤CD=11.其中正确结论的序号是( )
A.①②③④ B.①④⑤ C.①②④ D.③④⑤
【考点】正方形的性质;三角形的面积;全等三角形的判定与性质;等腰三角形的判定;勾股定理.
【专题】几何综合题;矩形 菱形 正方形;推理能力.
【答案】C
【分析】①利用SAS即可证明△APD≌△AEB,进而可以判断①正确;②根据△APD≌△AEB和等腰直角三角形的性质得出∠APE=∠AEP=45°,得出∠APD=∠AEB=135°,进而可以判断②正确;③根据勾股定理计算可得EB的长,进而可以判断③;④连接BD,可得S△APD+S△APB=S△AEP+S△EPB=33,即可判断④;⑤根据S△ABD=S△APD+S△APB+S△BPD=33+32=65,进而可以判断⑤.
【解答】解:①在正方形ABCD,AB=AD,∠BAD=90°,
∵EA⊥PA,
∴∠EAP=∠BAD=90°
∴∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
∵AE=AP,
在△APD和△AEB中,
,
∴△APD≌△AEB(SAS);故①成立;
②∵AE=AP=3,∠EAP=90°,
∴∠AEP=∠APE=45°,PEAE=6,
∵△APD≌△AEB,
∴∠AEB=∠APD=180°﹣45°=135°,故②成立;
③∴∠BEP=135°﹣45°=90°,
∴EB⊥ED,
在Rt△BPE中,PE=6,PB=10,
∴BE8,故③不成立;
④如图,连接BD,
由②得:PE=6,BE=8,
∵△APD≌△AEB,
∴S△APD+S△APB
=S△AEB+S△APB
=S四边形AEBP
=S△AEP+S△EPB
AE AP PE BE
336×8
=33.故④成立;
∵△APD≌△AEB,
∴PD=BE=8,
∴S△BDPPD BE=32,
∴S△ABD=S△APD+S△APB+S△BPD=33+32=65,
∴S正方形ABCD=2S△ABD=130,
∴CD2=130,
∴CD,故⑤不成立.
综上所述,正确结论的序号是①②④,
故选:C.
【点评】本题考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等是解题的关键.
3.(2024 沙坪坝区模拟)如图,正方形ABCD中,点E为边BA延长线上一点,点F在边BC上,且AE=CF,连接DF,EF.若∠FDC=α.则∠AEF=( )
A.90°﹣2α B.45°﹣α C.45°+α D.α
【考点】正方形的性质;全等三角形的判定与性质.
【专题】矩形 菱形 正方形;运算能力.
【答案】B
【分析】连接ED,根据正方形的性质可得∠ADC=∠BAD=∠C=90°,AD=DC,再由全等三角形的判定与性质可得∠FDC=∠ADE=α,最后由等腰直角三角形的性质及三角形外角性质可得答案.
【解答】解:连接ED,
在正方形ABCD中,∠ADC=∠BAD=∠C=90°,AD=DC,
∵AE=CF,
∴Rt△ADE≌Rt△CDF(SAS),
∴∠FDC=∠ADE=α,DE=DF,
∴∠CDF+∠ADF=∠ADE+∠ADF=90°,
∴∠EFD=∠FED=45°,
∴∠AGE=∠FED+∠ADE=45°+α,
∴∠AEF=90°﹣∠AGE=90°﹣(45°+α)=45°﹣α,
故选:B.
【点评】此题考查的是正方形的性质、全等三角形的判定与性质,正确作出辅助线是解决此题的关键.
4.(2024春 任泽区期末)小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是( )
A.(1)处可填∠A=90° B.(2)处可填AD=AB
C.(3)处可填DC=CB D.(4)处可填∠B=∠D
【考点】正方形的判定;菱形的判定;矩形的判定.
【专题】矩形 菱形 正方形;推理能力.
【答案】D
【分析】根据正方形、矩形、菱形的判定定理判断即可.
【解答】解:A、有一个角是直角的平行四边形是矩形,
∴(1)处可填∠A=90°是正确的,故该选项不符合题意;
B、一组邻边相等的矩形是正方形,
∴(2)处可填AD=AB是正确的,故该选项不符合题意;
C、一组邻边相等的平行四边形是菱形,
∴(3)处可填DC=CB是正确的,故该选项不符合题意;
D、有一个角是直角的菱形是正方形,
∴∠B=∠D无法判定两角是不是直角,故该选项不符合题意;
故选:D.
【点评】本题主要考查了矩形的判定,正方形的判定和菱形的判定,熟练掌握特殊四边形的关系是解题的关键.
5.(2024春 河西区期末)如图,在正方形ABCD外侧作等边△ADE,则∠AEB的度数为( )
A.15° B.22.5° C.20° D.10°
【考点】正方形的性质;等边三角形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;几何直观.
【答案】A
【分析】由四边形ABCD是正方形,△ADE是正三角形可得AB=AE,利用正方形和正三角形的内角性质即可得答案.
【解答】解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
又∵△ADE是正三角形,
∴AE=AD,∠DAE=60°,
∴△ABE是等腰三角形,∠BAE=90°+60°=150°,
∴∠ABE=∠AEB=15°.
故选:A.
【点评】本题题主要考查了正方形和等边三角形的性质,同时也利用了三角形的内角和,解题首先利用正方形和等边三角形的性质证明等腰三角形,然后利用等腰三角形的性质即可解决问题.
二.填空题(共5小题)
6.(2024 德州模拟)如图,点E在正方形ABCD的对角线AC上,EF⊥AB于点F,连接DE并延长,交边BC于点M,交边AB的延长线于点G.若AF=2,FB=1,则MG= .
【考点】正方形的性质.
【专题】图形的全等;矩形 菱形 正方形;图形的相似;推理能力.
【答案】.
【分析】由正方形性质得:BC=CD=AB=AF+FB=2+1=3,∠ABC=∠CBG=90°,DC∥AG,运用平行线成比例定理得,由DC∥AG,可得△CDE∽△AGE,求得AG=2CD=6,BG=3=CD,再证得△CDM≌△BGM(AAS),可得CM=BMBC,运用勾股定理即可求得答案.
【解答】解:∵四边形ABCD是正方形,AF=2,FB=1,
∴BC=CD=AB=AF+FB=2+1=3,∠ABC=∠CBG=90°,DC∥AG,
∵EF⊥AB,
∴∠AFE=90°,
∴∠AFE=∠ABC,
∴EF∥BC,
∴,
∵DC∥AG,
∴△CDE∽△AGE,
∴,
∴AG=2CD=6,
∴BG=AG﹣AB=6﹣3=3,
∴BG=CD,
∵CD∥AG,
∴∠CDM=∠G,
在△CDM和△BGM中,
,
∴△CDM≌△BGM(AAS),
∴CM=BMBC,
在Rt△BGM中,MG.
故答案为:.
【点评】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,平行线分线段成比例定理等,解题关键是熟练运用相似三角形的判定和性质.
7.(2024 平江县二模)如图,在Rt△ABC中,AB=4,点M是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则S△ABC= .
【考点】正方形的性质;三角形的面积;直角三角形斜边上的中线.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;几何直观;运算能力;推理能力.
【答案】.
【分析】先根据正方形的面积公式求出AM=4,再根据直角三角形的性质得BC=2AM=8,进而利用勾股定理求出AC,然后根据直角三角形的面积公式可求出△ABC的面积.
【解答】解:∵四边形AMEF为正方形,
∴S正方形AMEF=AM2,
又∵S正方形AMEF=16,
∴AM2=16,
∴AM=4,
在Rt△ABC中,点M是斜边BC的中点,
∴BC=2AM=8,
在Rt△ABC中,BC=8,AB=4,
由勾股定理得:AC,
∴S△ABCAB AC4.
故答案为:.
【点评】此题主要考查了正方形的面积,直角三角形的面积,直角三角形的性质,熟练掌握正方形和直角三角形的面积公式,理解直角三角形斜边上的中线等于斜边的一半是解决问题的关键.
8.(2024 甘肃一模)已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 5 .
【考点】正方形的性质;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形.
【答案】见试题解答内容
【分析】根据正方形的四条边都相等可得AB=AD,每一个角都是直角可得∠BAE=∠D=90°,然后利用“边角边”证明△ABE≌△DAF得∠ABE=∠DAF,进一步得∠AGE=∠BGF=90°,从而知GHBF,利用勾股定理求出BF的长即可得出答案.
【解答】解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
∵AB=AD,∠BAE=∠D,AE=DF
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GHBF,
∵BC=8,CF=CD﹣DF=8﹣2=6
∴BF10
∴GH=5
故答案为:5
【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形两锐角互余等知识,掌握三角形全等的判定方法与正方形的性质是解题的关键.
9.(2024春 兰陵县期末)如图,四边形ABCD和四边形AEFG均为正方形,点D为EF的中点,若AB=2,连接BF,则BF的长为 .
【考点】正方形的性质.
【专题】矩形 菱形 正方形;运算能力;推理能力.
【答案】.
【分析】连接AF,让△ADF绕点A顺时针旋转90°,此时AD与AB重合,得到△ABF′,连接EF′,根据旋转的性质得到△ADF≌△ABF′,再证明△AEF≌△AEF′,可得F,E,F′三点共线,根据三线合一得到FF′的值,最后利用角度的等量转换得到∠FF′B=90°,再根据勾股定理,即可解答.
【解答】解:如图,连接AF,让△ADF绕点A顺时针旋转90°,此时AD与AB重合,得到△ABF′,连接EF′,
∵四边形ABCD和四边形AEFG均为正方形,
∴EF=EA,∠FEA=90°,AD=AB,
根据旋转的性质,可得△ADF≌△ABF′,∠FAF′=90°,∠FAD=∠F′AB,
∴AF=AF′,∠AFE=∠AF′E=45°,
∴∠FAE=90°﹣∠AFF′=45°=∠DAF+∠DAE,
∴∠DAE+∠BAF′=45°,
∴∠EAF′=∠DAB﹣(∠DAE+∠BAF′)=45°,
∴△FAE≌△F′AE(SAS),
∴∠AEF=∠AEF′=90°,
可得F,E,F′三点共线,
∵∠AEF=90°,AF=AF′,
∴EF=EF′,
∵点D为EF的中点,
∴,
设ED=x,则AE=2x,
根据勾股定理可得,AE2+ED2=AD2,
即,
解得x=2(舍去负值),
∴EF=AE=4,BF′=DF=2,
∵AE⊥FF′,AF=AF′,
∴EF=EF′=4,
∴FF′=8,
∵∠EAF+∠AF′B=45°+45°=90°,
∴,
故答案为:.
【点评】本题考查了旋转的性质,全等三角形的性质,正方形的性质,等腰三角形的判定和性质,勾股定理,正确画出辅助线,耐心推理是解题的关键.
10.(2024 武进区校级二模)如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 .
【考点】正方形的性质;角平分线的性质.
【专题】矩形 菱形 正方形;图形的相似;运算能力;推理能力.
【答案】见试题解答内容
【分析】过点F作FM⊥CE于M,作FN⊥CD于点N,首先证四边形CMFN为正方形,再设CM=a,则FM=FN=CM=CN=a,BE=5,EM=2﹣a,然后证△EFM和△EAB相似,由相似三角形的性质求出a,进而在Rt△AFN中由勾股定理即可求出DF.
【解答】解:过点F作FM⊥CE于M,作FN⊥CD于点N,
∵四边形ABCD为正方形,AB=3,
∴∠ABC=90°,BC=AB=CD=3,AB∥CD,
∵FM⊥CE,FN⊥CD,∠DCE=∠B=90°,
∴四边形CMFN为矩形,
又∵CF平分∠DCE,FM⊥CE,FN⊥CD,
∴FM=FN,
∴四边形CMFN为正方形,
∴FM=FN=CM=CN,
设CM=a,则FM=FN=CM=CN=a,
∵CE=2,
∴BE=BC+CE=5,EM=CE﹣CM=2﹣a,
∵∠B=90°,FM⊥CE,
∴FM∥AB,
∴△EFM∽△EAB,
∴FM:AB=EM:BE,
即:a:3=(2﹣a):5,
解得:,
∴,
∴,
在Rt△DFN中,,,
由勾股定理得:.
故答案为:.
【点评】此题主要考查了正方形的判定及性质,相似三角形的判定和性质,勾股定理等,解答此题的关键是熟练掌握相似三角形的判定方法,理解相似三角形的对应边成比例.
三.解答题(共5小题)
11.(2024春 建湖县期中)如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,求证:四边形DEFG是正方形.
【考点】正方形的判定与性质;全等三角形的判定与性质;矩形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】见解析.
【分析】过点E分别作EM⊥BC于点M,EN⊥CD于点N,证明四边形EMCN为正方形,则EM=EN,∠MEN=90°,证明△DEN≌△FEM(ASA),得到ED=EF,即可得到结论.
【解答】证明:如图,过点E分别作EM⊥BC于点M,EN⊥CD于点N,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ECN=∠ECM=45°,
∴∠EMC=∠ENC=∠BCD=90°,
∴NE=NC,
∴四边形EMCN为正方形,
∴EM=EN,∠MEN=90°,
∵四边形DEFG是矩形,
∴∠DEF=90°,
∴∠DEN+∠NEF=∠FEM+∠NEF=90°,
∴∠DEN=∠FEM,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形.
【点评】此题考查了正方形的判定和性质、矩形的性质、全等三角形的判定和性质、角平分线的性质等知识,证明△DEN≌△FEM(ASA)是解题的关键.
12.(2024 萍乡期末)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上点,过点D作DE⊥BC交直线MN与E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形CDBE是什么特殊四边形?说明理由;
(3)在满足(2)的条件下,当△ABC再满足 等腰直角三角形 条件时,四边形CDBE是正方形(直接填写答案).
【考点】正方形的判定.
【专题】矩形 菱形 正方形;推理能力.
【答案】(1)见解析;
(2)四边形BECD是菱形,理由见解析;
(3)当△ABC是等腰直角三角形时,四边形BECD是正方形;理由见解析.
【分析】(1)证出AC∥DE,得出四边形ADEC是平行四边形,即可得出结论;
(2)先证出BD=CE,得出四边形BECD是平行四边形,再由直角三角形斜边上的中线性质得出CDAB=BD,即可得出四边形BECD是菱形;
(3)当△ABC是等腰直角三角形,由等腰三角形的性质得出CD⊥AB,即可得出四边形BECD是正方形.
【解答】(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,理由如下:
∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CDAB=BD,
∴四边形BECD是菱形;
(3)解:当△ABC是等腰直角三角形时,四边形BECD是正方形;理由如下:
∵∠ACB=90°,
当△ABC是等腰直角三角形,
∵D为AB的中点,
∴CD⊥AB,
∴∠CDB=90°,
∴四边形BECD是正方形,
故答案为:等腰直角三角形.
【点评】本题考查了平行四边形的判定与性质、正方形的判定、菱形的判定、直角三角形斜边上的中线性质;熟练掌握平行四边形的判定与性质,并能进行推理论证是解决问题的关键.
13.(2024春 信阳期末)如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
【考点】正方形的判定与性质;角平分线的性质;含30度角的直角三角形.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;几何直观;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)根据有三个角是直角的四边形是矩形,可得四边形OGCF是矩形,根据角平分线的性质,可得OH与OF,OH与OG的关系,根据邻边相等的矩形是正方形,可得答案;
(2)由含30°角的直角三角形的性质和勾股定理求出AB和BC,根据全等三角形判定的HL定理证得Rt△AOH≌Rt△AOF得到AH=AF,设正方形OGCF的边长为x,则AH=AF=4﹣x,BH=BG=4x,根据AB=AH+BH=8,解方程即可求出x.
【解答】(1)证明:过O作OH⊥AB于H点,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的角平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF,
又四边形OGCF是矩形,
∴四边形OGCF是正方形;
(2)解:在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=90°﹣60°=30°,
∴ACAB,
∵AC=4,
∴AB=2AC=2×4=8,
∵AC2+BC2=AB2,
∴BC4,
在Rt△AOH和Rt△AOF中,
,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF的边长为x,
则AH=AF=4﹣x,BH=BG=4x,
∴4﹣x+4x=8,
∴x=22,
即正方形OGCF的边长为22.
【点评】本题主要考查了正方形的判定和性质,角平分线的性质,全等三角形的判定和性质,含30°角的直角三角形的性质和勾股定理,正确作出辅助线,且根据角平分线的性质推出OH=OF=OG是解决问题的关键.
14.(2024春 河北期末)如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
【考点】正方形的判定与性质;全等三角形的判定与性质;矩形的性质.
【专题】证明题;矩形 菱形 正方形;推理能力.
【答案】(1)证明过程见解答;
(2)①证明过程见解答;
②3.
【分析】(1)根据正方形的性质证明△ABE≌△ADE(SAS),即可解决问题;
(2)①作EM⊥BC于M,EN⊥CD于N,得到EN=EM,然后证得∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF,根据正方形的判定即可证得矩形DEFG是正方形;
②证明△ADE≌△CDG(SAS),可得AE=CG,∠DAE=∠DCG=45°,证明CE⊥CG,连接EG,根据勾股定理即可解决问题.
【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
【点评】此题主要考查了正方形的判定与性质,矩形的性质,三角形的全等的性质和判定,勾股定理,解本题的关键是正确作出辅助线,证得△DEN≌△FEM.
15.(2024春 易门县期末)如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
【考点】正方形的性质;全等三角形的判定与性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【答案】(1)见解析;
(2)见解析;
(3).
【分析】(1)根据正方形的性质得到AD=AB,AD∥BC,根据全等三角形的性质即可得到结论;
(2)延长BC至F,且使CF=BC,连接AF,则BM=CE,由SAS证明△ABF≌△DCE,得出∠DEC=∠AFB,证出MN为△AEF的中位线,得出MN∥AF,得出∠HNE=∠AFB=∠HEN,即可得出HE=HN;
(3)过点B作BQ⊥BP交DE于Q,由ASA证明△BEQ≌△BAP,得出PA=QE,QB=PB,证出△PBQ是等腰直角三角形,由勾股定理得出PQPB,即可得出答案;
【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,AD∥BC,
∴∠DAB=∠ABE,∠ADO=∠BEO,
∵AB=BE,
∴AD=BE,
∴△ADO≌△BEO(ASA),
∴AO=BO;
(2)证明:延长BC至F,且使CF=BC,连接AF,如图1所示:
则BF=CE,
∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=∠ABC=∠DCB=90°,
在△ABF和△DCE中,,
∴△ABF≌△DCE(SAS),
∴∠DEC=∠AFB,
∵EB=CF,BN=CN,
∴N为EF的中点,
∴MN为△AEF的中位线,
∴MN∥AF,
∴∠HNB=∠AFB=∠HEB;
(3)解:过点B作BQ⊥BP交DE于Q,如图2所示:
则∠PBQ=90°,
∵∠ABE=180°﹣∠ABC=90°,
∴∠EBQ=∠ABP,
∵AD∥BC,
∴∠ADP=∠BEQ,
∵AP⊥DE,∠BAD=90°,
由角的互余关系得:∠BAP=∠ADP,
∴∠BEQ=∠BAP,
在△BEQ和△BAP中,,
∴△BEQ≌△BAP(ASA),
∴PA=QE,QB=PB,
∴△PBQ是等腰直角三角形,
∴PQPB,
∴.
【点评】本题考查了正方形的性质、全等三角形的判定与性质、平行线的性质、等腰直角三角形的判定与性质、勾股定理、直角三角形的性质等知识;本题综合性强,有一定难度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
