2026年中考《数学》复习课件：专题四 三角形--第19讲 全等三角形 (共44张PPT)

(共44张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
第19讲 全等三角形
聚焦核心
1.全等三角形的性质与判定
性质 对应边______，对应角______ 判定 “边边边”或“ ” 三边分别______的两个三角形全等
“边角边”或“ ” 两边和它们的______分别相等的两个
三角形全等
“角边角”或“ ” 两角和它们的______分别相等的两个
三角形全等
相等
相等
相等
夹角
夹边
判定 “角角边”或“ ” 两角和其中一个角的______分别相等
的两个三角形全等
“斜边、直角边”或“ ” ______和一条直角边分别相等的两个
直角三角形全等
对边
斜边
续表
2.角平分线的性质与判定
性质 ________________________________________________________________ __________________________________
判定 ________________________________________________________________
平分（或）
第19讲 全等三角形
案例分析
考点一 全等三角形的性质
名师指导
全等三角形的对应边相等，对应角相等，这是求角的度数、线段长
度，证明线段或角相等的常用到的性质.运用全等三角形的性质的关键
是找准对应边和对应角.
图1
例1 （2025·广西崇左·模拟）如图1，
，点在线段上， ，
则 的度数是( ).
A
A. B. C. D.
提示：由，得 ，，.从而得 ， .所以 ，即 .
思路点拨 与 是对应角，根据全等三角形的对应角相等可知，
要求，求出的度数即可.在 中，由全等三角形的对应边相
等得，则求出的度数，即可得到 的度数.
考点专练
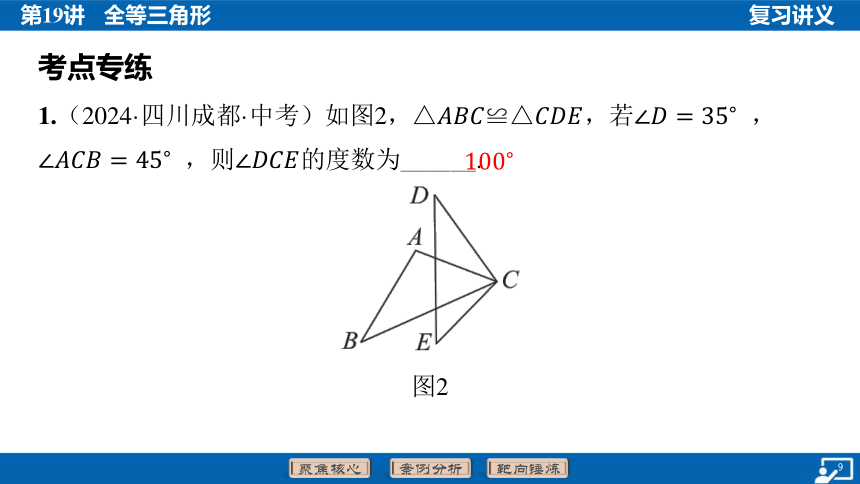
1.（2024·四川成都·中考）如图2，，若 ，
，则 的度数为______.
图2
2.（2024·甘肃临夏·中考）如图3，在中，点的坐标为 ，点
的坐标为，点的坐标为，点在第一象限（不与点 重合），
且与全等，点 的坐标是______.
图3
3.如图4，已知，点，，， 在同一条直线上．
图4
（1）当，时，求线段 的长．
解：，
，，
.
（2）请判断与 的位置关系，并说明理由．
图4
解.
理由：，
.
考点二 全等三角形的判定
名师指导
1.判定三角形全等的常用思路：
（1）已知两边对应相等，找它们的夹角对应相等（用“”判定），
或找第三边对应相等（用“”判定），或找直角（用“”或“”判
定）；
（2）已知两角对应相等，必须找一边对应相等（用“”或“”
判定）；
（3）已知一边一角，当已知一角及其邻边时，找这个角的另一邻
边对应相等（用“”判定），或找另一角对应相等（用“”或“ ”
判定）；当已知一角及其对边时，找另一角对应相等（用“ ”判
定）．
2.判定全等三角形时，注意利用图形中隐含的条件：
（1）公共角 两个三角形中对应相等的角；
（2）对顶角 两个三角形中对应相等的角；
（3）公共边或相等的线段 两个三角形中对应相等的边.
图5
例2 （2024·四川内江·中考）如图5，点， ，
，在同一条直线上，， ，
.
（1）求证： .
证明：，，即.
在 和中，，，，
.
思路点拨（1）已知， ，且没有给出有关角的已知条件，则考虑依据“”判定和 全等，由已知条件推出 即可得证.
图5
（2）已知 ， ，求 的度数.
解：， ， .
， .
思路点拨 （2）根据（1）的结论，由全等三角形的性质可得对应角相等，再结合三角形内角和定理可得 的度数
考点专练
图6
4.（2025·四川凉山·中考模拟）如图6,点,在 上,
, .添加一个条件,不能证明
的是( ).
D
A. B.
C. D.
图7
5.（2024·四川乐山·中考）如图7，是 的平分
线，.求证： .
证明：是的平分线， .
在和中，， ，，
.
图8
6.（2025·江苏南通·中考模拟）如图8，点， 分别在，上， ，， 相交于点， .
求证： .
小明的证明过程如下：
证明： ，
.
，
第一步
又， ，
第二步
第三步
（1）小明的证明过程中，第___步出现错误.
二
图8
（2）请写出正确的证明过程.
证明：∵ ， .
在和中， ，，，∴
.
在 和R中，，，
.
（方法二）同方法一得 ，即，，平分 .
考点三 角平分线的性质与判定
名师指导
遇到角平分线，我们要想到两个结论：
（1）平分角（得到两个相等的角）；
（2）角平分线上的点到角两边的距离相等（用于证明线段相等或
进行有关线段的计算）.
例3 教材变式［沪科版八上第150页第10题变式］如图9，在四边形中， ，为的中点，且平分 .
图9
（1）求证：平分 .
思路点拨（1）
证明:如图21,过点作于点.
又 ,平分,
为的中点,
.
又∵ ⊥ , , 平分 .
图21
（2）求证： .
图9
思维点拨（2）思路一：
思路二：利用平行线的判定和性质，得出 ，再利
用角平分线的定义和三角形内角和定理，即可证得结论.
解：一题多解 （方法一）在和 中,
,,
.
同理可得
. .
,
.
图9
平分, 平分， ,
.
.
.
图9
（3）求证： .
图9
解：由（2）知，， .
同理可得
， .
思维点拨（3）
考点专练
图10
7.（2024·青海·中考）如图10，平分，点
在上，于点，，则点到 的
距离是( ).
C
A.4 B.3 C.2 D.1
图11
8.（2025·湖南株洲·中考模拟）如图11，点 在一块直角
三角尺内部（其中），
于点，于点.若，则
____ .
15
图12
9.如图12，是的平分线，，点 在
上，，，垂足分别是点， .
求证： ．
证明：是的平分线，.
又 ，，∴
，即 平分．
又，， ．
第19讲 全等三角形
靶向锤炼
靶向练
图1
1.（2024·山东济南·中考）如图1，已知
， ， ，则
的度数为( ).
C
A. B. C. D.
图2
2.（2025·广西梧州·中考改编）如图2，在 中，
，是的角平分线，过点 分别作
，，垂足分别是点， ，则下列结论
不一定成立的是( ).
C
A. B.
C. D.
图3
3.（2025·四川成都·中考模拟）如图3，已知
，点，，， 依次在同一条直
线上.若，，则 的长为___.
3
4.（2024·黑龙江牡丹江·中考）如图4，在中，是 上一点，
，，， 三点共线，请添加一个条件_____________________
_________________，使得 .（只添加一个条件即可）
（答案不唯一）（或）
图4
5.（2024·江苏镇江·中考）如图5， ， .
图5
（1）求证： .
证明：在和中，，， ， .
（2）当 时，求 的度数.
图5
解： ， ， .
由（1）知， .
攻坚练
图6
6.（2025·广西柳州·模拟）如图6，在四边形
中， ，，，对角线 平分
，则 的面积为( ).
B
A.15 B.12 C.8 D.6
图7
7.（2024·广东广州·中考）如图7，在 中，
，，为边 的中点，点
，分别在边，上， ，则四边形
的面积为( ).
C
A.18 B. C.9 D.
提示：连接，由 ，，D为边 的中点，得
， ， .又
，所以.从而得 .故四边形
的面积 .
图8
8.（2025·广西崇左·模拟）如图8，一个等腰直角三角形
物件斜靠在墙角处.若 ，
，则点到地面的距离是____ .
30
提示：过点作于点 ，由 ，得 ，所以.又，所以 .由此可得， .
图9
9.如图9，，交的延长线于点 ，
于点，， ．
（1）求证：平分 .
证明： ，， .
和 均为直角三角形.
和中，，，
平分 .
（2）直接写出与 之间的等量关系．
图9
提示：在和中，，，
．
解： ．
10.数学文化（2025·甘肃兰州·中考改编）综合与实践
【问题探究】
（1）图10是欧几里得在《几何原本》中给出的角平分线
作图法：在和上分别取点和，使得 ，
连接，以为边作等边三角形，则就是
的平分线．请写出平分 的依据：____.
提示：因为是等边三角形，所以 .又因为
，，所以 .所以
.所以是 的平分线.
图10
冲刺练
【类比迁移】
图11
（2）小明根据以上信息研究发现： 不一定必须是
等边三角形，只需 即可.他查阅资料发现，我国
古代已经用角尺平分任意角，做法如下：如图11，在
的边，上分别取 ，移动角尺，使角
尺两边相同刻度分别与点，重合，则过角尺顶点 的
射线是 的平分线，请说明此做法的理由.
解：在和中，，，，
射线是 的平分线.
【拓展实践】
（3）小明将研究应用于实践．如图12，校园的两条小路和 ，汇聚
形成了一个岔路口，现在学校要在两条小路之间安装一盏路灯 ，使
得路灯照亮两条小路（两条小路一样亮），并且路灯到岔路口 的距
离和休息椅到岔路口 的距离相等，试问路灯应该安装在哪个位置？
请用不带刻度的直尺和圆规在对应的示意图13中作出路灯 的位置.
（保留作图痕迹，不写作法）
图12
图13
【答案】如图24，点 即为所求位置．
图24