2.4自由落体运动(预习衔接.含解析)2025-2026学年高一上学期物理必修第一册人教版(2019)
文档属性
| 名称 | 2.4自由落体运动(预习衔接.含解析)2025-2026学年高一上学期物理必修第一册人教版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-09 21:14:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
新课预习衔接 自由落体运动
一.选择题(共5小题)
1.(2024 南开区期末)关于以下两个斜面实验的说法中正确的是( )
A.伽利略使用图甲斜面进行实验,得出力不是维持物体运动的原因
B.牛顿使用图甲斜面进行实验,得出自由落体运动的规律
C.伽利略使用图乙斜面进行实验,得出力不是维持物体运动的原因
D.牛顿使用图乙斜面进行实验,得出自由落体运动的规律
2.(2024春 南宁期末)高空坠物给社会带来很大危害。从21楼由静止下落的酒瓶,落地时的速度大小约为(每层楼高约3米,重力加速度大小为10m/s2,不计空气阻力,1.73)( )
A.25m/s B.30m/s C.35m/s D.40m/s
3.(2024 莲湖区校级模拟)如图所示,小球甲从距离地面高度为h1=15m处以速度v0=10m/s竖直向上抛出,同时小球乙从距离地面高度为h2=20m处开始自由下落,小球运动的过程中不计空气阻力,重力加速度取g=10m/s2,则下列说法中正确的是( )
A.小球乙落地前,两小球的速度差逐渐变大
B.落地前的运动过程中小球甲、乙的平均速率之比为5:6
C.至小球乙落地时,甲、乙两球的位移大小之比为3:4
D.小球甲、乙运动的第1s内位移相同
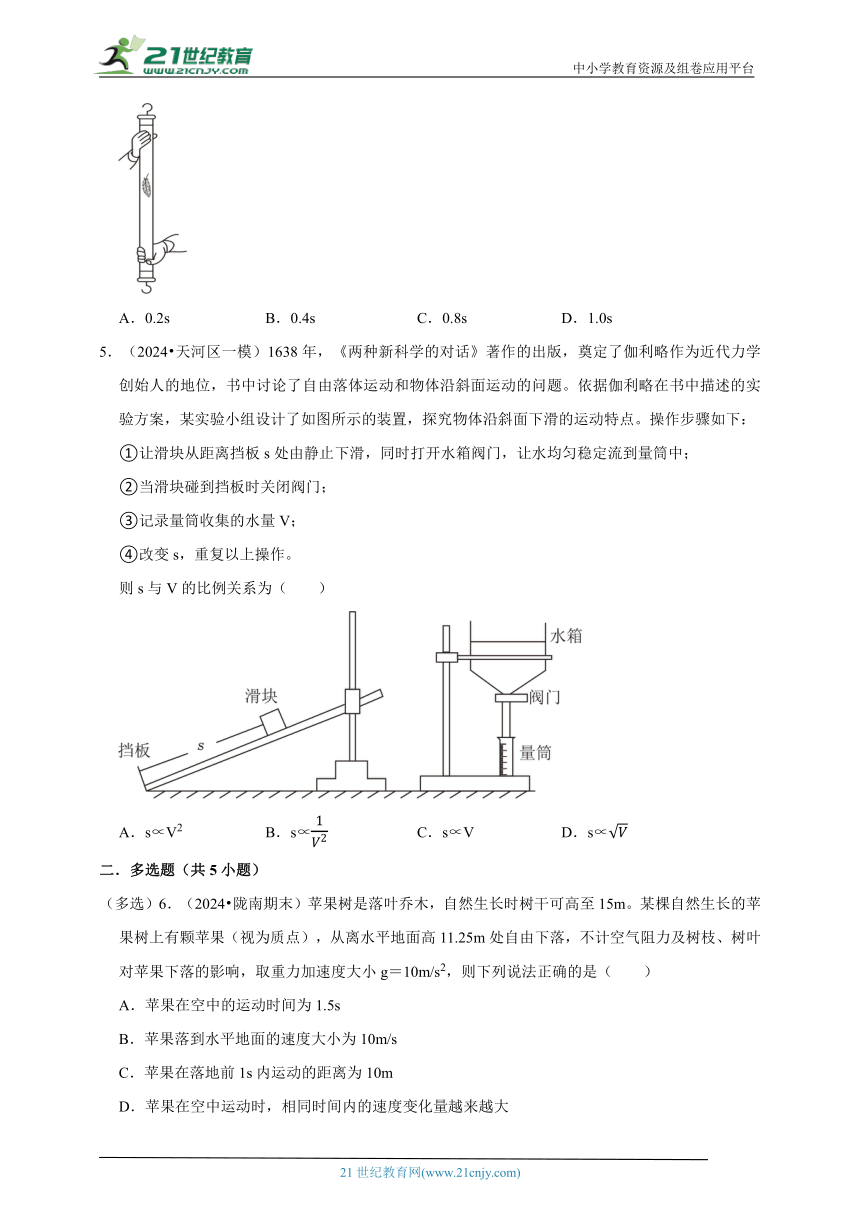
4.(2024 长寿区期末)如图所示,将长度为0.8m的牛顿管抽成真空后,快速倒置,则管中羽毛从顶端下落到管底的时间约为( )
A.0.2s B.0.4s C.0.8s D.1.0s
5.(2024 天河区一模)1638年,《两种新科学的对话》著作的出版,奠定了伽利略作为近代力学创始人的地位,书中讨论了自由落体运动和物体沿斜面运动的问题。依据伽利略在书中描述的实验方案,某实验小组设计了如图所示的装置,探究物体沿斜面下滑的运动特点。操作步骤如下:
①让滑块从距离挡板s处由静止下滑,同时打开水箱阀门,让水均匀稳定流到量筒中;
②当滑块碰到挡板时关闭阀门;
③记录量筒收集的水量V;
④改变s,重复以上操作。
则s与V的比例关系为( )
A.s∝V2 B.s∝ C.s∝V D.s∝
二.多选题(共5小题)
(多选)6.(2024 陇南期末)苹果树是落叶乔木,自然生长时树干可高至15m。某棵自然生长的苹果树上有颗苹果(视为质点),从离水平地面高11.25m处自由下落,不计空气阻力及树枝、树叶对苹果下落的影响,取重力加速度大小g=10m/s2,则下列说法正确的是( )
A.苹果在空中的运动时间为1.5s
B.苹果落到水平地面的速度大小为10m/s
C.苹果在落地前1s内运动的距离为10m
D.苹果在空中运动时,相同时间内的速度变化量越来越大
(多选)7.(2024 晋江市校级月考)下列说法正确的是( )
A.伽利略的斜面实验是牛顿第一定律的实验基础
B.物体不受外力作用时,一定处于静止状态
C.力是改变物体运动状态的原因
D.物体的运动不需要力来维持,但物体的运动速度越大时其惯性也越大
(多选)8.(2024 长安区校级期末)如图所示,在足够高的空间内,小球位于空心管的正上方h处,空心管长为L,小球球心与管的轴线重合,并在竖直线上。当释放小球,小球可能穿过空心管,不计空气阻力,则下列判断正确的是( )
A.两者同时无初速度释放,小球能穿过空心管
B.两者均无初速度释放,但小球提前了Δt时间释放,则小球一定能穿过管
C.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球定能穿过管,但穿过管的时间
D.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球一定能穿过管,但穿过管的时间
(多选)9.(2024 河东区校级期末)从高度为125m的塔顶,先后落下a、b两球,自由释放这两个球的时间差为1s,则以下判断正确的是(g取10m/s2,不计空气阻力)( )
A.b球下落高度为20m时,a球的速度大小为20m/s
B.a球接触地面瞬间,b球离地高度为45m
C.在a球接触地面之前,两球的速度差恒定
D.在a球接触地面之前,两球离地的高度差恒定
(多选)10.(2024 沈阳期末)如图所示,乙球静止于地面上,甲球位于乙球正上方h处,现从地面上竖直上抛乙球,初速度v0=10m/s,同时让甲球自由下落,不计空气阻力。(取g=10m/s2,甲乙两球可看作质点)下列说法正确的是( )
A.无论h为何值,甲乙两球一定能在空中相遇
B.当h=10m时,乙球恰好在最高点与甲球相遇
C.当h=15m时,乙球能在下降过程中与甲球相遇
D.当h<10m时,乙球能在上升过程中与甲球相遇
三.解答题(共5小题)
11.(2024 吉林期末)某校一课外活动小组自制一枚火箭,设火箭从地面发射后,始终在垂直于地面的方向上运动。火箭点火后可认为做匀加速直线运动,经过2s到达离地面40m高处时燃料恰好用完,接着做竖直上抛运动。若不计空气阻力,取g=10m/s2,求:
(1)燃料恰好用完时火箭的速度;
(2)火箭上升离地面的最大高度;
(3)火箭从发射到残骸落回地面过程的总时间(计算结果用根号表示)。
12.(2024 西湖区校级期末)某同学将一橡皮球从离地高为H处由静止释放,落地后橡皮球第一次反弹高度为h=0.80m,已知橡皮球与地面第一次碰撞时间为t0=0.2s,碰撞前后速度大小之比为3:2,小球运动过程中所受空气阻力可忽略不计(重力加速度g取10m/s2),试求:
(1)橡皮球与地面第一次碰撞前的速度及释放时离地的高度H;
(2)橡皮球从释放至第一次反弹最高处所用时间。
13.(2024 琼山区校级模拟)质量为m的小球以速度v0由水平地面竖直向上抛出,经多次与地面碰撞后,最终静止在地面上。已知小球与地面的碰撞为弹性碰撞,重力加速度记为g,运动过程中小球所受空气阻力视为恒定,大小为0.6mg。求小球
(1)从抛出到静止所经历的总路程;
(2)向上运动与向下运动的时间之比。
14.(2024 碑林区校级期末)节日里放的起花最早出自《儒林外史》,描述“形如小纸炮,缀有长约二三尺苇杆,燃其芯即急起”。设起花从地面发射后始终在竖直方向上运动,点火后可认为做初速度为0、加速度a=8m/s2的匀加速直线运动,当到达离地面高h=25m时燃料恰好用完。若不计空气阻力、忽略重力的变化,重力加速度g=10m/s2,求:
(1)起花上升的最大高度H;
(2)起花返回地面时的速度v;
(3)起花在空中运动的总时间t。
15.(2024 琼山区校级模拟)小敏在学过自由落体运动规律后,对自家房上下落的雨滴产生了兴趣,她坐在窗前发现从屋檐每隔相等时间滴下一滴水,当第5滴正欲滴下时,第1滴刚好落到地面,而第3滴与第2滴分别位于高1m的窗子的上、下沿。小敏同学在自己的作业本上画出了如图所示的雨滴下落同自家房子的关系,其中2点和3点之间的小矩形表示小敏正对的窗子(g取10m/s2),求:
(1)滴水的时间间隔。
(2)此屋檐离地面多高。
新课预习衔接 自由落体运动
参考答案与试题解析
一.选择题(共5小题)
1.(2024 南开区期末)关于以下两个斜面实验的说法中正确的是( )
A.伽利略使用图甲斜面进行实验,得出力不是维持物体运动的原因
B.牛顿使用图甲斜面进行实验,得出自由落体运动的规律
C.伽利略使用图乙斜面进行实验,得出力不是维持物体运动的原因
D.牛顿使用图乙斜面进行实验,得出自由落体运动的规律
【考点】伽利略对自由落体运动的探究;力学物理学史.
【专题】定性思想;推理法;牛顿运动定律综合专题;推理能力.
【答案】C
【分析】伽利略利用图甲斜面进行实验,得出自由落体运动的规律;利用图乙实验得出力是改变物体运动状态的原因。
【解答】解:AB.根据图甲可知,因为当时无法测量物体的瞬时速度,伽利略设想物体下落的速度与时间成正比,所以伽利略通过数学推导证明:如果速度与时间成正比,那么位移与时间的平方成正比;由于当时用滴水法计算,无法记录自由落体的较短时间,伽利略设计了让铜球沿阻力很小的斜面滚下,来“冲淡“重力的作用效果,而小球在斜面上运动的加速度要比它竖直下落的加速度小得多,所用时间长的多,所以容易测量。伽利略做了上百次实验,并通过抽象思维在实验结果上做了合理外推,得到了自由落体运动的规律,故AB错误;
CD.根据图乙可知,伽利略用抽象思维、数学推导和科学实验相结合的方法得到力不是维持物体运动的原因,故C正确,D错误。
故选:C。
【点评】本题考查伽利略斜坡实验,不同的实验得出的实验结论是不同的,需平时对实验原理与实验结论加强掌握。
2.(2024春 南宁期末)高空坠物给社会带来很大危害。从21楼由静止下落的酒瓶,落地时的速度大小约为(每层楼高约3米,重力加速度大小为10m/s2,不计空气阻力,1.73)( )
A.25m/s B.30m/s C.35m/s D.40m/s
【考点】自由落体运动的规律及应用.
【专题】计算题;定量思想;推理法;自由落体运动专题;推理能力.
【答案】C
【分析】根据自由落体运动的速度—位移公式可求解。
【解答】解:由题意可知,酒瓶做自由落体运动,下落的高度为:h=20×3m=60m,根据v2=2gh,得vm/s≈34.6m/s,故C正确,ABD错误;
故选:C。
【点评】本题主要考查对于自由落体的理解和计算。
3.(2024 莲湖区校级模拟)如图所示,小球甲从距离地面高度为h1=15m处以速度v0=10m/s竖直向上抛出,同时小球乙从距离地面高度为h2=20m处开始自由下落,小球运动的过程中不计空气阻力,重力加速度取g=10m/s2,则下列说法中正确的是( )
A.小球乙落地前,两小球的速度差逐渐变大
B.落地前的运动过程中小球甲、乙的平均速率之比为5:6
C.至小球乙落地时,甲、乙两球的位移大小之比为3:4
D.小球甲、乙运动的第1s内位移相同
【考点】竖直上抛运动的规律及应用;匀变速直线运动规律的综合应用.
【专题】定量思想;推理法;直线运动规律专题;推理能力.
【答案】B
【分析】由速度变化量求解速度关系,由自由落体及竖直上抛公式求解时间,并进一步求解平均速率比值,由位移—时间关系求解位移。
【解答】解:A.取竖直向上为正方向,甲球跟乙球的速度差为Δv=v0﹣gt﹣(﹣gt)=v0,故A错误;
B.由hgt2
得乙球落地用时间为
t2=2s
对甲球:由v0t115
解得
t1=3s
甲球经过的路程为25m,乙球经过的路程为20m,那么落地前的运动过程中小球甲、乙的平均速率之比为5:6,故B正确;
C.乙球落地时,甲球的位移为0,即恰好回到抛出点,则至小球乙落地时,甲、乙两球的位移大小之比为0,故C错误;
D.对甲球,第1s内位移x'm=5m,对乙球,第1s内位移x'm=5m,两位移方向不同,故D错误。
故选:B。
【点评】本题考查匀速直线运动,学生需结合运动学公式综合分析解答。
4.(2024 长寿区期末)如图所示,将长度为0.8m的牛顿管抽成真空后,快速倒置,则管中羽毛从顶端下落到管底的时间约为( )
A.0.2s B.0.4s C.0.8s D.1.0s
【考点】自由落体运动的规律及应用.
【专题】定量思想;推理法;自由落体运动专题;理解能力.
【答案】B
【分析】牛顿管抽成真空后,羽毛从顶端下落到管底的过程可看作只受重力作用,可看作自由落体运动,根据位移公式求解即可。
【解答】解:牛顿管抽成真空后,羽毛从顶端下落到管底的过程可看自由落体运动,
由位移公式得:h,t
h=0.8m,g取10m/s2,解得:t=0.4s,故ACD错误B正确;
故选:B。
【点评】牛顿管抽成真空后,没有了空气的阻力,忽略摩擦,可看作自由落体运动求解。
5.(2024 天河区一模)1638年,《两种新科学的对话》著作的出版,奠定了伽利略作为近代力学创始人的地位,书中讨论了自由落体运动和物体沿斜面运动的问题。依据伽利略在书中描述的实验方案,某实验小组设计了如图所示的装置,探究物体沿斜面下滑的运动特点。操作步骤如下:
①让滑块从距离挡板s处由静止下滑,同时打开水箱阀门,让水均匀稳定流到量筒中;
②当滑块碰到挡板时关闭阀门;
③记录量筒收集的水量V;
④改变s,重复以上操作。
则s与V的比例关系为( )
A.s∝V2 B.s∝ C.s∝V D.s∝
【考点】伽利略对自由落体运动的探究.
【专题】定性思想;推理法;直线运动规律专题;理解能力.
【答案】A
【分析】通过匀变速直线运动的位移—时间公式找到位移与时间的关系,再处理水的体积与时间的关系即可。
【解答】解:滑块在粗糙程度相同的斜面上由静止释放,可知滑块做初速度为零的匀加速直线运动,根据运动学公式有sat2,即s与t2成正比。由于水均匀稳定流到量筒中,所以量筒中收集的水的体积V与t成正比,则有s∝t2∝V2,故A正确,BCD错误。
故选:A。
【点评】本题主要考查了匀变速直线运动位移与时间的关系,解题关键是分析小球的运动,通过运动学公式找到位移与时间的关系,再处理水的体积与时间的关系即可。
二.多选题(共5小题)
(多选)6.(2024 陇南期末)苹果树是落叶乔木,自然生长时树干可高至15m。某棵自然生长的苹果树上有颗苹果(视为质点),从离水平地面高11.25m处自由下落,不计空气阻力及树枝、树叶对苹果下落的影响,取重力加速度大小g=10m/s2,则下列说法正确的是( )
A.苹果在空中的运动时间为1.5s
B.苹果落到水平地面的速度大小为10m/s
C.苹果在落地前1s内运动的距离为10m
D.苹果在空中运动时,相同时间内的速度变化量越来越大
【考点】自由落体运动的规律及应用.
【专题】定量思想;推理法;自由落体运动专题;推理能力.
【答案】AC
【分析】由题可知,苹果做自由落体运动,根据自由落体运动的规律和运动学公式求解即可。
【解答】解:A.由题可知,苹果做自由落体运动,则根据自由落体运动的位移—时间关系可得:
解得苹果在空中的运动时间为:t1.5s,故A正确;
B.苹果落到水平地面的速度大小为:v=gt=10×1.5m/s=15m/s,故B错误;
C.苹果在落地前1s内运动的距离为:,故C正确;
D.苹果在空中运动时,相同时间内的速度变化量为:Δv=gΔt,可知相同时间内的速度变化量不变,故D错误。
故选:AC。
【点评】解题关键是掌握自由落体运动的规律和运动学公式。难度不大。
(多选)7.(2024 晋江市校级月考)下列说法正确的是( )
A.伽利略的斜面实验是牛顿第一定律的实验基础
B.物体不受外力作用时,一定处于静止状态
C.力是改变物体运动状态的原因
D.物体的运动不需要力来维持,但物体的运动速度越大时其惯性也越大
【考点】伽利略对自由落体运动的探究;牛顿第一定律的内容与应用;惯性与质量;力学物理学史.
【专题】定性思想;推理法;牛顿运动定律综合专题;分析综合能力.
【答案】AC
【分析】牛顿在前人研究成果的基础上提出了牛顿第一定律,伽利略的斜面实验是牛顿第一定律的实验基础;物体不受外力作用,一定处于静止状态或者是匀速直线运动状态;力是改变物体运动状态的原因;物体的运动不需要力来维持;质量是影响惯性大小的唯一量度。据此分析。
【解答】解:A、牛顿在前人研究成果的基础上提出了牛顿第一定律,伽利略的斜面实验是牛顿第一定律的实验基础,故A正确;
B、根据牛顿第一定律,物体不受外力作用,一定处于静止状态或者是匀速直线运动状态,故B错误;
C、力是改变物体运动状态的原因,故C正确;
D、物体的运动不需要力来维持;质量是影响惯性大小的唯一量度,惯性与速度无关,故D错误。
故选:AC。
【点评】解答本题的关键是知道力是改变物体运动状态的原因,而不是维持物体运动状态的原因,物体不受力时将处于静止状态或匀速直线运动状态。
(多选)8.(2024 长安区校级期末)如图所示,在足够高的空间内,小球位于空心管的正上方h处,空心管长为L,小球球心与管的轴线重合,并在竖直线上。当释放小球,小球可能穿过空心管,不计空气阻力,则下列判断正确的是( )
A.两者同时无初速度释放,小球能穿过空心管
B.两者均无初速度释放,但小球提前了Δt时间释放,则小球一定能穿过管
C.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球定能穿过管,但穿过管的时间
D.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球一定能穿过管,但穿过管的时间
【考点】自由落体运动的规律及应用;匀变速直线运动位移与时间的关系.
【专题】定量思想;推理法;自由落体运动专题;推理能力.
【答案】BC
【分析】根据匀变速直线运动的位移—时间公式,抓住位移之差等于L+h进行分析求解。
【解答】解:A、若两者无初速度同时释放,则在相同时间内下降的高度相同,可知小球在空中不能穿过管,故A错误。
B、两者均无初速度释放,但小球提前了Δt时间释放,根据Δxg(t+Δt)2 gt2gΔt2+gt Δt=h+L.可知小球能穿过管,穿过管的时间与当地的重力加速度有关。故B正确。
CD、两者同时释放,小球具有向下的初速度v0,管无初速度,两者加速度相同均为g,以管为参考系,小球相对于管做匀速直线运动,小球到达管的上端所用时间为:t1,小球到达管的下端所用时间为:t2,小球穿过管的时间为t=t2﹣t1,故C正确,D错误。
故选:BC。
【点评】本题主要考查了自由落体运动的规律,解决本题的关键掌握匀变速直线运动的运动学公式,抓住位移之差等于h+L进行求解。
(多选)9.(2024 河东区校级期末)从高度为125m的塔顶,先后落下a、b两球,自由释放这两个球的时间差为1s,则以下判断正确的是(g取10m/s2,不计空气阻力)( )
A.b球下落高度为20m时,a球的速度大小为20m/s
B.a球接触地面瞬间,b球离地高度为45m
C.在a球接触地面之前,两球的速度差恒定
D.在a球接触地面之前,两球离地的高度差恒定
【考点】自由落体运动的规律及应用.
【专题】自由落体运动专题.
【答案】BC
【分析】A、求出b球下落20m所用的时间,从而知道a球运动时间,根据v=gt求出a球的速度.
B、求出a球与地面接触所用的时间,从而知道b球运动的时间,根据求出b球下落的高度,从而得知b球离地的高度.
C、求出两球速度变化量与时间是否有关,从而确定速度差是否恒定.
D、求出两球下落的高度差是否与时间有关,从而确定高度差是否恒定.
【解答】解:A、根据知,b球下落的时间.则a球下落的时间t1=3s,速度v=gt1=30m/s。故A错误。
B、a球运动的时间,则b球的运动时间t′=4s,b球下降的高度,所以b球离地面的高度为45m。故B正确。
C、设b球下降时间为t时,b球的速度vb=gt,a球的速度va=g(t+1),则Δv=va﹣vb=g,与时间无关,是一定量。故C正确。
D、设b球下降时间为t时,b球下降的高度,a球下降的高度,两球离地的高度差等于下降的高度差,,随时间的增大,位移差增大。故D错误。
故选:BC。
【点评】解决本题的关键知道自由落体运动中,相隔一定时间释放一个小球,在小球落地前,两球的速度差恒定,两球离地的高度差不恒定.
(多选)10.(2024 沈阳期末)如图所示,乙球静止于地面上,甲球位于乙球正上方h处,现从地面上竖直上抛乙球,初速度v0=10m/s,同时让甲球自由下落,不计空气阻力。(取g=10m/s2,甲乙两球可看作质点)下列说法正确的是( )
A.无论h为何值,甲乙两球一定能在空中相遇
B.当h=10m时,乙球恰好在最高点与甲球相遇
C.当h=15m时,乙球能在下降过程中与甲球相遇
D.当h<10m时,乙球能在上升过程中与甲球相遇
【考点】自由落体运动的规律及应用;竖直上抛运动的规律及应用.
【专题】比较思想;模型法;直线运动规律专题;分析综合能力.
【答案】BCD
【分析】根据甲球与乙球相遇时两者位移之和等于h,求出相遇时间与h的关系,再根据竖直上抛运动的规律确定h的范围。
【解答】解:设甲球与乙球经过时间t相遇,则有h(v0t),得t
根据竖直上抛运动的规律,可知,乙球上升的时间为t上s=1s,乙球竖直上抛运动的总时间t总=2t上=2s
A、甲乙两球能在空中相遇,必须满足:t<t总,即2s,得h<20m,即当h<20m时,甲乙两球一定能在空中相遇;当h>20m时,甲乙两球不能在空中相遇,故A错误;
B、当t=t上时,即1s,得h=10m,乙球恰好在最高点与甲球相遇,故B正确;
C、当t上<t<t总时,乙球能在下降过程中与甲球相遇,即1s2s,得10m<h<20m,故当h=15m时,乙球能在下降过程中与甲球相遇,故C正确;
D、当t<t上时,乙球能在上升过程中与甲球相遇,即1s,得h<10m,故D正确。
故选:BCD。
【点评】本题是自由落体运动与竖直上抛运动相遇的问题,关键要掌握竖直上抛运动的规律,根据相遇时间与竖直上抛运动上升时间和总时间关系,来判断乙球在什么过程与甲球相遇。
三.解答题(共5小题)
11.(2024 吉林期末)某校一课外活动小组自制一枚火箭,设火箭从地面发射后,始终在垂直于地面的方向上运动。火箭点火后可认为做匀加速直线运动,经过2s到达离地面40m高处时燃料恰好用完,接着做竖直上抛运动。若不计空气阻力,取g=10m/s2,求:
(1)燃料恰好用完时火箭的速度;
(2)火箭上升离地面的最大高度;
(3)火箭从发射到残骸落回地面过程的总时间(计算结果用根号表示)。
【考点】竖直上抛运动的规律及应用;匀变速直线运动规律的综合应用;匀变速直线运动位移与时间的关系.
【专题】计算题;信息给予题;定量思想;推理法;直线运动规律专题;推理能力.
【答案】(1)燃料恰好用完时火箭的速度为40m/s,方向竖直向上;
(2)火箭上升离地面的最大高度为120m;
(3)火箭从发射到残骸落回地面过程的总时间为。
【分析】(1)分析火箭的上升运动过程,根据匀变速直线运动规律计算;
(2)根据位移与速度关系公式计算;
(3)根据速度—时间关系式和位移—时间关系式计算。
【解答】解:(1)设燃料用完时火箭的速度为v1,所用时间为t1。火箭的上升运动分为两个过程,第一过程做匀加速上升运动,第二个过程做竖直上抛运动至最高点,对第一个过程,自制火箭做匀加速运动有
解得
a=20m/s2
由速度公式得
v1=at1=20×2m/s=40m/s
方向竖直向上;
(2)对第二个过程,由位移与速度关系公式得
代入数据解得
h2=80m
所以火箭上升离地面的最大高度
h=h1+h2=40m+80m=120m
(3)从燃料用完到运动至最高点的过程中,有
v1=gt2
解得
从最高点落回地面的过程中
解得
故总时间为
答:(1)燃料恰好用完时火箭的速度为40m/s,方向竖直向上;
(2)火箭上升离地面的最大高度为120m;
(3)火箭从发射到残骸落回地面过程的总时间为。
【点评】本题关键掌握火箭运动过程的分析和匀变速直线运动规律的使用。
12.(2024 西湖区校级期末)某同学将一橡皮球从离地高为H处由静止释放,落地后橡皮球第一次反弹高度为h=0.80m,已知橡皮球与地面第一次碰撞时间为t0=0.2s,碰撞前后速度大小之比为3:2,小球运动过程中所受空气阻力可忽略不计(重力加速度g取10m/s2),试求:
(1)橡皮球与地面第一次碰撞前的速度及释放时离地的高度H;
(2)橡皮球从释放至第一次反弹最高处所用时间。
【考点】竖直上抛运动的规律及应用;自由落体运动的规律及应用.
【专题】计算题;学科综合题;定量思想;方程法;自由落体运动专题;推理能力.
【答案】(1)橡皮球与地面第一次碰撞前的速度为6m/s,释放时离地的高度H为1.8m;
(2)橡皮球从释放至第一次反弹最高处所用时间为1.2s。
【分析】(1)根据速度—位移公式求出橡皮球与地面第一次碰撞前的速度,根据速度关系求出碰撞前的速度,然后求出释放时离地的高度H;
(2)根据速度—时间公式求出上升的时间与下落的时间,然后求和。
【解答】解:(1)设橡皮球与地面碰撞前、后的速度大小分别为v1,v2;碰撞后橡皮球上升过程,有
代入数据得:v2=4m/s
橡皮球碰撞前后v1:v2=3:2
联立解得v1=6m/s
橡皮球自由下落过程,有
得:H=1.8m
(2)橡皮球下落过程有v1=gt1
橡皮球反弹过程有v2=gt2
橡皮球从释放至反弹最高处所用时间为Δt=t1+t0+t2
联立解得Δt=1.2s
答:(1)橡皮球与地面第一次碰撞前的速度为6m/s,释放时离地的高度H为1.8m;
(2)橡皮球从释放至第一次反弹最高处所用时间为1.2s。
【点评】本题考查了自由落体运动和竖直上抛运动,要抓住竖直上抛运动的对称性来解题;小球每次与地面发生碰撞前后的速度大小之比是解题关键所在。
13.(2024 琼山区校级模拟)质量为m的小球以速度v0由水平地面竖直向上抛出,经多次与地面碰撞后,最终静止在地面上。已知小球与地面的碰撞为弹性碰撞,重力加速度记为g,运动过程中小球所受空气阻力视为恒定,大小为0.6mg。求小球
(1)从抛出到静止所经历的总路程;
(2)向上运动与向下运动的时间之比。
【考点】竖直上抛运动的规律及应用.
【专题】定量思想;推理法;直线运动规律专题;推理能力.
【答案】(1)从抛出到静止所经历的总路程为;
(2)向上运动与向下运动的时间之比为1:2。
【分析】(1)可利用动能定理计算位移;
(2)小球上升过程做匀减速直线运动,上升到最高点开始向下做匀加速直线运动,可分别计算利用牛顿第二定律计算加速度,利用加速度定义式分别计算向上运动的时间和向下运动的时间,进而计算比值。
【解答】解:(1)由于小球与地面发生弹性碰撞,没有机械能损失,由初状态到末状态由动能定理得
整理解得:
(2)上升过程由牛顿第二定律可知加速度为
整理解得a1=1.6g
下降过程由牛顿第二定律可知加速度为
上升和下降阶段速度的位移大小相等,则有
a上t上2a下t下2
整理解得t上:t下=1:2。
答:(1)从抛出到静止所经历的总路程为;
(2)向上运动与向下运动的时间之比为1:2。
【点评】本题考查了对竖直上抛运动的理解,其中旨在考查对匀变速直线运动规律的理解。
14.(2024 碑林区校级期末)节日里放的起花最早出自《儒林外史》,描述“形如小纸炮,缀有长约二三尺苇杆,燃其芯即急起”。设起花从地面发射后始终在竖直方向上运动,点火后可认为做初速度为0、加速度a=8m/s2的匀加速直线运动,当到达离地面高h=25m时燃料恰好用完。若不计空气阻力、忽略重力的变化,重力加速度g=10m/s2,求:
(1)起花上升的最大高度H;
(2)起花返回地面时的速度v;
(3)起花在空中运动的总时间t。
【考点】竖直上抛运动的规律及应用;匀变速直线运动规律的综合应用;匀变速直线运动位移与时间的关系.
【专题】计算题;定量思想;推理法;直线运动规律专题;推理能力.
【答案】见试题解答内容
【分析】(1)起花先向上做匀加速直线运动,后向上做匀减速直线运动,根据匀变速直线运动位移—速度公式列式求解两段高度,两高度之和即为上升的最大高度;
(2)起花下落过程做自由落体运动,根据自由落体运动位移—速度公式列式求解即可;
(3)根据速度—时间公式求解上升过程的时间,根据位移—时间公式求解下落过程的时间,三段时间之和即为在空中运动的总时间。
【解答】解:(1)设燃料用完时速度为v1,有:
设之后上升的高度为Δh,有:
代入数据联立解得:Δh=20m
起花上升的最大高度为:h+Δh=25m+20m=45m
(2)下落过程,根据自由落体运动位移—速度公式得:v2=2gH
代入数据解得:v=30m/s
(3)设起花加速上升的时间为t1,减速上升的时间为t2,自由下落的时间为t3,加速上升过程:v1=at1
减速上升过程:0=v1﹣gt2
下落过程:H
起花在空中运动的总时间为:t=t1+t2+t3
代入数据联立解得:t=7.5s
答:(1)起花上升的最大高度H为45m;
(2)起花返回地面时的速度v为30m/s;
(3)起花在空中运动的总时间t为7.5s。
【点评】本题考查匀变速直线运动,解题关键是分析好起花的运动过程,掌握匀变速直线运动的规律并能够熟练应用。
15.(2024 琼山区校级模拟)小敏在学过自由落体运动规律后,对自家房上下落的雨滴产生了兴趣,她坐在窗前发现从屋檐每隔相等时间滴下一滴水,当第5滴正欲滴下时,第1滴刚好落到地面,而第3滴与第2滴分别位于高1m的窗子的上、下沿。小敏同学在自己的作业本上画出了如图所示的雨滴下落同自家房子的关系,其中2点和3点之间的小矩形表示小敏正对的窗子(g取10m/s2),求:
(1)滴水的时间间隔。
(2)此屋檐离地面多高。
【考点】自由落体运动的规律及应用.
【专题】定量思想;比例法;自由落体运动专题;理解能力;推理能力.
【答案】(1)滴水的时间间隔为0.2s;
(2)此屋檐离地面3.2m
【分析】(2)由初速度等于零的匀加速直线运动的规律解答;(1)由自由落体规律计算雨滴下落时间,再定滴水间隔。
【解答】解:(2)由初速度等于零的匀加速直线运动的规律:相邻相同时间间隔内位移比为1:3:5:7: :(2n﹣1),得屋檐离地高度:H3.2m,(1)由自由落体规律:H 得:t,所以滴水时间间隔为:t′
答:(1)滴水的时间间隔为0.2s;
(2)此屋檐离地面3.2m
【点评】熟记初速度等于零的匀加速直线运动的各种推论,提高解题效率。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 自由落体运动
一.选择题(共5小题)
1.(2024 南开区期末)关于以下两个斜面实验的说法中正确的是( )
A.伽利略使用图甲斜面进行实验,得出力不是维持物体运动的原因
B.牛顿使用图甲斜面进行实验,得出自由落体运动的规律
C.伽利略使用图乙斜面进行实验,得出力不是维持物体运动的原因
D.牛顿使用图乙斜面进行实验,得出自由落体运动的规律
2.(2024春 南宁期末)高空坠物给社会带来很大危害。从21楼由静止下落的酒瓶,落地时的速度大小约为(每层楼高约3米,重力加速度大小为10m/s2,不计空气阻力,1.73)( )
A.25m/s B.30m/s C.35m/s D.40m/s
3.(2024 莲湖区校级模拟)如图所示,小球甲从距离地面高度为h1=15m处以速度v0=10m/s竖直向上抛出,同时小球乙从距离地面高度为h2=20m处开始自由下落,小球运动的过程中不计空气阻力,重力加速度取g=10m/s2,则下列说法中正确的是( )
A.小球乙落地前,两小球的速度差逐渐变大
B.落地前的运动过程中小球甲、乙的平均速率之比为5:6
C.至小球乙落地时,甲、乙两球的位移大小之比为3:4
D.小球甲、乙运动的第1s内位移相同
4.(2024 长寿区期末)如图所示,将长度为0.8m的牛顿管抽成真空后,快速倒置,则管中羽毛从顶端下落到管底的时间约为( )
A.0.2s B.0.4s C.0.8s D.1.0s
5.(2024 天河区一模)1638年,《两种新科学的对话》著作的出版,奠定了伽利略作为近代力学创始人的地位,书中讨论了自由落体运动和物体沿斜面运动的问题。依据伽利略在书中描述的实验方案,某实验小组设计了如图所示的装置,探究物体沿斜面下滑的运动特点。操作步骤如下:
①让滑块从距离挡板s处由静止下滑,同时打开水箱阀门,让水均匀稳定流到量筒中;
②当滑块碰到挡板时关闭阀门;
③记录量筒收集的水量V;
④改变s,重复以上操作。
则s与V的比例关系为( )
A.s∝V2 B.s∝ C.s∝V D.s∝
二.多选题(共5小题)
(多选)6.(2024 陇南期末)苹果树是落叶乔木,自然生长时树干可高至15m。某棵自然生长的苹果树上有颗苹果(视为质点),从离水平地面高11.25m处自由下落,不计空气阻力及树枝、树叶对苹果下落的影响,取重力加速度大小g=10m/s2,则下列说法正确的是( )
A.苹果在空中的运动时间为1.5s
B.苹果落到水平地面的速度大小为10m/s
C.苹果在落地前1s内运动的距离为10m
D.苹果在空中运动时,相同时间内的速度变化量越来越大
(多选)7.(2024 晋江市校级月考)下列说法正确的是( )
A.伽利略的斜面实验是牛顿第一定律的实验基础
B.物体不受外力作用时,一定处于静止状态
C.力是改变物体运动状态的原因
D.物体的运动不需要力来维持,但物体的运动速度越大时其惯性也越大
(多选)8.(2024 长安区校级期末)如图所示,在足够高的空间内,小球位于空心管的正上方h处,空心管长为L,小球球心与管的轴线重合,并在竖直线上。当释放小球,小球可能穿过空心管,不计空气阻力,则下列判断正确的是( )
A.两者同时无初速度释放,小球能穿过空心管
B.两者均无初速度释放,但小球提前了Δt时间释放,则小球一定能穿过管
C.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球定能穿过管,但穿过管的时间
D.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球一定能穿过管,但穿过管的时间
(多选)9.(2024 河东区校级期末)从高度为125m的塔顶,先后落下a、b两球,自由释放这两个球的时间差为1s,则以下判断正确的是(g取10m/s2,不计空气阻力)( )
A.b球下落高度为20m时,a球的速度大小为20m/s
B.a球接触地面瞬间,b球离地高度为45m
C.在a球接触地面之前,两球的速度差恒定
D.在a球接触地面之前,两球离地的高度差恒定
(多选)10.(2024 沈阳期末)如图所示,乙球静止于地面上,甲球位于乙球正上方h处,现从地面上竖直上抛乙球,初速度v0=10m/s,同时让甲球自由下落,不计空气阻力。(取g=10m/s2,甲乙两球可看作质点)下列说法正确的是( )
A.无论h为何值,甲乙两球一定能在空中相遇
B.当h=10m时,乙球恰好在最高点与甲球相遇
C.当h=15m时,乙球能在下降过程中与甲球相遇
D.当h<10m时,乙球能在上升过程中与甲球相遇
三.解答题(共5小题)
11.(2024 吉林期末)某校一课外活动小组自制一枚火箭,设火箭从地面发射后,始终在垂直于地面的方向上运动。火箭点火后可认为做匀加速直线运动,经过2s到达离地面40m高处时燃料恰好用完,接着做竖直上抛运动。若不计空气阻力,取g=10m/s2,求:
(1)燃料恰好用完时火箭的速度;
(2)火箭上升离地面的最大高度;
(3)火箭从发射到残骸落回地面过程的总时间(计算结果用根号表示)。
12.(2024 西湖区校级期末)某同学将一橡皮球从离地高为H处由静止释放,落地后橡皮球第一次反弹高度为h=0.80m,已知橡皮球与地面第一次碰撞时间为t0=0.2s,碰撞前后速度大小之比为3:2,小球运动过程中所受空气阻力可忽略不计(重力加速度g取10m/s2),试求:
(1)橡皮球与地面第一次碰撞前的速度及释放时离地的高度H;
(2)橡皮球从释放至第一次反弹最高处所用时间。
13.(2024 琼山区校级模拟)质量为m的小球以速度v0由水平地面竖直向上抛出,经多次与地面碰撞后,最终静止在地面上。已知小球与地面的碰撞为弹性碰撞,重力加速度记为g,运动过程中小球所受空气阻力视为恒定,大小为0.6mg。求小球
(1)从抛出到静止所经历的总路程;
(2)向上运动与向下运动的时间之比。
14.(2024 碑林区校级期末)节日里放的起花最早出自《儒林外史》,描述“形如小纸炮,缀有长约二三尺苇杆,燃其芯即急起”。设起花从地面发射后始终在竖直方向上运动,点火后可认为做初速度为0、加速度a=8m/s2的匀加速直线运动,当到达离地面高h=25m时燃料恰好用完。若不计空气阻力、忽略重力的变化,重力加速度g=10m/s2,求:
(1)起花上升的最大高度H;
(2)起花返回地面时的速度v;
(3)起花在空中运动的总时间t。
15.(2024 琼山区校级模拟)小敏在学过自由落体运动规律后,对自家房上下落的雨滴产生了兴趣,她坐在窗前发现从屋檐每隔相等时间滴下一滴水,当第5滴正欲滴下时,第1滴刚好落到地面,而第3滴与第2滴分别位于高1m的窗子的上、下沿。小敏同学在自己的作业本上画出了如图所示的雨滴下落同自家房子的关系,其中2点和3点之间的小矩形表示小敏正对的窗子(g取10m/s2),求:
(1)滴水的时间间隔。
(2)此屋檐离地面多高。
新课预习衔接 自由落体运动
参考答案与试题解析
一.选择题(共5小题)
1.(2024 南开区期末)关于以下两个斜面实验的说法中正确的是( )
A.伽利略使用图甲斜面进行实验,得出力不是维持物体运动的原因
B.牛顿使用图甲斜面进行实验,得出自由落体运动的规律
C.伽利略使用图乙斜面进行实验,得出力不是维持物体运动的原因
D.牛顿使用图乙斜面进行实验,得出自由落体运动的规律
【考点】伽利略对自由落体运动的探究;力学物理学史.
【专题】定性思想;推理法;牛顿运动定律综合专题;推理能力.
【答案】C
【分析】伽利略利用图甲斜面进行实验,得出自由落体运动的规律;利用图乙实验得出力是改变物体运动状态的原因。
【解答】解:AB.根据图甲可知,因为当时无法测量物体的瞬时速度,伽利略设想物体下落的速度与时间成正比,所以伽利略通过数学推导证明:如果速度与时间成正比,那么位移与时间的平方成正比;由于当时用滴水法计算,无法记录自由落体的较短时间,伽利略设计了让铜球沿阻力很小的斜面滚下,来“冲淡“重力的作用效果,而小球在斜面上运动的加速度要比它竖直下落的加速度小得多,所用时间长的多,所以容易测量。伽利略做了上百次实验,并通过抽象思维在实验结果上做了合理外推,得到了自由落体运动的规律,故AB错误;
CD.根据图乙可知,伽利略用抽象思维、数学推导和科学实验相结合的方法得到力不是维持物体运动的原因,故C正确,D错误。
故选:C。
【点评】本题考查伽利略斜坡实验,不同的实验得出的实验结论是不同的,需平时对实验原理与实验结论加强掌握。
2.(2024春 南宁期末)高空坠物给社会带来很大危害。从21楼由静止下落的酒瓶,落地时的速度大小约为(每层楼高约3米,重力加速度大小为10m/s2,不计空气阻力,1.73)( )
A.25m/s B.30m/s C.35m/s D.40m/s
【考点】自由落体运动的规律及应用.
【专题】计算题;定量思想;推理法;自由落体运动专题;推理能力.
【答案】C
【分析】根据自由落体运动的速度—位移公式可求解。
【解答】解:由题意可知,酒瓶做自由落体运动,下落的高度为:h=20×3m=60m,根据v2=2gh,得vm/s≈34.6m/s,故C正确,ABD错误;
故选:C。
【点评】本题主要考查对于自由落体的理解和计算。
3.(2024 莲湖区校级模拟)如图所示,小球甲从距离地面高度为h1=15m处以速度v0=10m/s竖直向上抛出,同时小球乙从距离地面高度为h2=20m处开始自由下落,小球运动的过程中不计空气阻力,重力加速度取g=10m/s2,则下列说法中正确的是( )
A.小球乙落地前,两小球的速度差逐渐变大
B.落地前的运动过程中小球甲、乙的平均速率之比为5:6
C.至小球乙落地时,甲、乙两球的位移大小之比为3:4
D.小球甲、乙运动的第1s内位移相同
【考点】竖直上抛运动的规律及应用;匀变速直线运动规律的综合应用.
【专题】定量思想;推理法;直线运动规律专题;推理能力.
【答案】B
【分析】由速度变化量求解速度关系,由自由落体及竖直上抛公式求解时间,并进一步求解平均速率比值,由位移—时间关系求解位移。
【解答】解:A.取竖直向上为正方向,甲球跟乙球的速度差为Δv=v0﹣gt﹣(﹣gt)=v0,故A错误;
B.由hgt2
得乙球落地用时间为
t2=2s
对甲球:由v0t115
解得
t1=3s
甲球经过的路程为25m,乙球经过的路程为20m,那么落地前的运动过程中小球甲、乙的平均速率之比为5:6,故B正确;
C.乙球落地时,甲球的位移为0,即恰好回到抛出点,则至小球乙落地时,甲、乙两球的位移大小之比为0,故C错误;
D.对甲球,第1s内位移x'm=5m,对乙球,第1s内位移x'm=5m,两位移方向不同,故D错误。
故选:B。
【点评】本题考查匀速直线运动,学生需结合运动学公式综合分析解答。
4.(2024 长寿区期末)如图所示,将长度为0.8m的牛顿管抽成真空后,快速倒置,则管中羽毛从顶端下落到管底的时间约为( )
A.0.2s B.0.4s C.0.8s D.1.0s
【考点】自由落体运动的规律及应用.
【专题】定量思想;推理法;自由落体运动专题;理解能力.
【答案】B
【分析】牛顿管抽成真空后,羽毛从顶端下落到管底的过程可看作只受重力作用,可看作自由落体运动,根据位移公式求解即可。
【解答】解:牛顿管抽成真空后,羽毛从顶端下落到管底的过程可看自由落体运动,
由位移公式得:h,t
h=0.8m,g取10m/s2,解得:t=0.4s,故ACD错误B正确;
故选:B。
【点评】牛顿管抽成真空后,没有了空气的阻力,忽略摩擦,可看作自由落体运动求解。
5.(2024 天河区一模)1638年,《两种新科学的对话》著作的出版,奠定了伽利略作为近代力学创始人的地位,书中讨论了自由落体运动和物体沿斜面运动的问题。依据伽利略在书中描述的实验方案,某实验小组设计了如图所示的装置,探究物体沿斜面下滑的运动特点。操作步骤如下:
①让滑块从距离挡板s处由静止下滑,同时打开水箱阀门,让水均匀稳定流到量筒中;
②当滑块碰到挡板时关闭阀门;
③记录量筒收集的水量V;
④改变s,重复以上操作。
则s与V的比例关系为( )
A.s∝V2 B.s∝ C.s∝V D.s∝
【考点】伽利略对自由落体运动的探究.
【专题】定性思想;推理法;直线运动规律专题;理解能力.
【答案】A
【分析】通过匀变速直线运动的位移—时间公式找到位移与时间的关系,再处理水的体积与时间的关系即可。
【解答】解:滑块在粗糙程度相同的斜面上由静止释放,可知滑块做初速度为零的匀加速直线运动,根据运动学公式有sat2,即s与t2成正比。由于水均匀稳定流到量筒中,所以量筒中收集的水的体积V与t成正比,则有s∝t2∝V2,故A正确,BCD错误。
故选:A。
【点评】本题主要考查了匀变速直线运动位移与时间的关系,解题关键是分析小球的运动,通过运动学公式找到位移与时间的关系,再处理水的体积与时间的关系即可。
二.多选题(共5小题)
(多选)6.(2024 陇南期末)苹果树是落叶乔木,自然生长时树干可高至15m。某棵自然生长的苹果树上有颗苹果(视为质点),从离水平地面高11.25m处自由下落,不计空气阻力及树枝、树叶对苹果下落的影响,取重力加速度大小g=10m/s2,则下列说法正确的是( )
A.苹果在空中的运动时间为1.5s
B.苹果落到水平地面的速度大小为10m/s
C.苹果在落地前1s内运动的距离为10m
D.苹果在空中运动时,相同时间内的速度变化量越来越大
【考点】自由落体运动的规律及应用.
【专题】定量思想;推理法;自由落体运动专题;推理能力.
【答案】AC
【分析】由题可知,苹果做自由落体运动,根据自由落体运动的规律和运动学公式求解即可。
【解答】解:A.由题可知,苹果做自由落体运动,则根据自由落体运动的位移—时间关系可得:
解得苹果在空中的运动时间为:t1.5s,故A正确;
B.苹果落到水平地面的速度大小为:v=gt=10×1.5m/s=15m/s,故B错误;
C.苹果在落地前1s内运动的距离为:,故C正确;
D.苹果在空中运动时,相同时间内的速度变化量为:Δv=gΔt,可知相同时间内的速度变化量不变,故D错误。
故选:AC。
【点评】解题关键是掌握自由落体运动的规律和运动学公式。难度不大。
(多选)7.(2024 晋江市校级月考)下列说法正确的是( )
A.伽利略的斜面实验是牛顿第一定律的实验基础
B.物体不受外力作用时,一定处于静止状态
C.力是改变物体运动状态的原因
D.物体的运动不需要力来维持,但物体的运动速度越大时其惯性也越大
【考点】伽利略对自由落体运动的探究;牛顿第一定律的内容与应用;惯性与质量;力学物理学史.
【专题】定性思想;推理法;牛顿运动定律综合专题;分析综合能力.
【答案】AC
【分析】牛顿在前人研究成果的基础上提出了牛顿第一定律,伽利略的斜面实验是牛顿第一定律的实验基础;物体不受外力作用,一定处于静止状态或者是匀速直线运动状态;力是改变物体运动状态的原因;物体的运动不需要力来维持;质量是影响惯性大小的唯一量度。据此分析。
【解答】解:A、牛顿在前人研究成果的基础上提出了牛顿第一定律,伽利略的斜面实验是牛顿第一定律的实验基础,故A正确;
B、根据牛顿第一定律,物体不受外力作用,一定处于静止状态或者是匀速直线运动状态,故B错误;
C、力是改变物体运动状态的原因,故C正确;
D、物体的运动不需要力来维持;质量是影响惯性大小的唯一量度,惯性与速度无关,故D错误。
故选:AC。
【点评】解答本题的关键是知道力是改变物体运动状态的原因,而不是维持物体运动状态的原因,物体不受力时将处于静止状态或匀速直线运动状态。
(多选)8.(2024 长安区校级期末)如图所示,在足够高的空间内,小球位于空心管的正上方h处,空心管长为L,小球球心与管的轴线重合,并在竖直线上。当释放小球,小球可能穿过空心管,不计空气阻力,则下列判断正确的是( )
A.两者同时无初速度释放,小球能穿过空心管
B.两者均无初速度释放,但小球提前了Δt时间释放,则小球一定能穿过管
C.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球定能穿过管,但穿过管的时间
D.两者同时释放,小球具有竖直向下的初速度v0,空心管无初速度,则小球一定能穿过管,但穿过管的时间
【考点】自由落体运动的规律及应用;匀变速直线运动位移与时间的关系.
【专题】定量思想;推理法;自由落体运动专题;推理能力.
【答案】BC
【分析】根据匀变速直线运动的位移—时间公式,抓住位移之差等于L+h进行分析求解。
【解答】解:A、若两者无初速度同时释放,则在相同时间内下降的高度相同,可知小球在空中不能穿过管,故A错误。
B、两者均无初速度释放,但小球提前了Δt时间释放,根据Δxg(t+Δt)2 gt2gΔt2+gt Δt=h+L.可知小球能穿过管,穿过管的时间与当地的重力加速度有关。故B正确。
CD、两者同时释放,小球具有向下的初速度v0,管无初速度,两者加速度相同均为g,以管为参考系,小球相对于管做匀速直线运动,小球到达管的上端所用时间为:t1,小球到达管的下端所用时间为:t2,小球穿过管的时间为t=t2﹣t1,故C正确,D错误。
故选:BC。
【点评】本题主要考查了自由落体运动的规律,解决本题的关键掌握匀变速直线运动的运动学公式,抓住位移之差等于h+L进行求解。
(多选)9.(2024 河东区校级期末)从高度为125m的塔顶,先后落下a、b两球,自由释放这两个球的时间差为1s,则以下判断正确的是(g取10m/s2,不计空气阻力)( )
A.b球下落高度为20m时,a球的速度大小为20m/s
B.a球接触地面瞬间,b球离地高度为45m
C.在a球接触地面之前,两球的速度差恒定
D.在a球接触地面之前,两球离地的高度差恒定
【考点】自由落体运动的规律及应用.
【专题】自由落体运动专题.
【答案】BC
【分析】A、求出b球下落20m所用的时间,从而知道a球运动时间,根据v=gt求出a球的速度.
B、求出a球与地面接触所用的时间,从而知道b球运动的时间,根据求出b球下落的高度,从而得知b球离地的高度.
C、求出两球速度变化量与时间是否有关,从而确定速度差是否恒定.
D、求出两球下落的高度差是否与时间有关,从而确定高度差是否恒定.
【解答】解:A、根据知,b球下落的时间.则a球下落的时间t1=3s,速度v=gt1=30m/s。故A错误。
B、a球运动的时间,则b球的运动时间t′=4s,b球下降的高度,所以b球离地面的高度为45m。故B正确。
C、设b球下降时间为t时,b球的速度vb=gt,a球的速度va=g(t+1),则Δv=va﹣vb=g,与时间无关,是一定量。故C正确。
D、设b球下降时间为t时,b球下降的高度,a球下降的高度,两球离地的高度差等于下降的高度差,,随时间的增大,位移差增大。故D错误。
故选:BC。
【点评】解决本题的关键知道自由落体运动中,相隔一定时间释放一个小球,在小球落地前,两球的速度差恒定,两球离地的高度差不恒定.
(多选)10.(2024 沈阳期末)如图所示,乙球静止于地面上,甲球位于乙球正上方h处,现从地面上竖直上抛乙球,初速度v0=10m/s,同时让甲球自由下落,不计空气阻力。(取g=10m/s2,甲乙两球可看作质点)下列说法正确的是( )
A.无论h为何值,甲乙两球一定能在空中相遇
B.当h=10m时,乙球恰好在最高点与甲球相遇
C.当h=15m时,乙球能在下降过程中与甲球相遇
D.当h<10m时,乙球能在上升过程中与甲球相遇
【考点】自由落体运动的规律及应用;竖直上抛运动的规律及应用.
【专题】比较思想;模型法;直线运动规律专题;分析综合能力.
【答案】BCD
【分析】根据甲球与乙球相遇时两者位移之和等于h,求出相遇时间与h的关系,再根据竖直上抛运动的规律确定h的范围。
【解答】解:设甲球与乙球经过时间t相遇,则有h(v0t),得t
根据竖直上抛运动的规律,可知,乙球上升的时间为t上s=1s,乙球竖直上抛运动的总时间t总=2t上=2s
A、甲乙两球能在空中相遇,必须满足:t<t总,即2s,得h<20m,即当h<20m时,甲乙两球一定能在空中相遇;当h>20m时,甲乙两球不能在空中相遇,故A错误;
B、当t=t上时,即1s,得h=10m,乙球恰好在最高点与甲球相遇,故B正确;
C、当t上<t<t总时,乙球能在下降过程中与甲球相遇,即1s2s,得10m<h<20m,故当h=15m时,乙球能在下降过程中与甲球相遇,故C正确;
D、当t<t上时,乙球能在上升过程中与甲球相遇,即1s,得h<10m,故D正确。
故选:BCD。
【点评】本题是自由落体运动与竖直上抛运动相遇的问题,关键要掌握竖直上抛运动的规律,根据相遇时间与竖直上抛运动上升时间和总时间关系,来判断乙球在什么过程与甲球相遇。
三.解答题(共5小题)
11.(2024 吉林期末)某校一课外活动小组自制一枚火箭,设火箭从地面发射后,始终在垂直于地面的方向上运动。火箭点火后可认为做匀加速直线运动,经过2s到达离地面40m高处时燃料恰好用完,接着做竖直上抛运动。若不计空气阻力,取g=10m/s2,求:
(1)燃料恰好用完时火箭的速度;
(2)火箭上升离地面的最大高度;
(3)火箭从发射到残骸落回地面过程的总时间(计算结果用根号表示)。
【考点】竖直上抛运动的规律及应用;匀变速直线运动规律的综合应用;匀变速直线运动位移与时间的关系.
【专题】计算题;信息给予题;定量思想;推理法;直线运动规律专题;推理能力.
【答案】(1)燃料恰好用完时火箭的速度为40m/s,方向竖直向上;
(2)火箭上升离地面的最大高度为120m;
(3)火箭从发射到残骸落回地面过程的总时间为。
【分析】(1)分析火箭的上升运动过程,根据匀变速直线运动规律计算;
(2)根据位移与速度关系公式计算;
(3)根据速度—时间关系式和位移—时间关系式计算。
【解答】解:(1)设燃料用完时火箭的速度为v1,所用时间为t1。火箭的上升运动分为两个过程,第一过程做匀加速上升运动,第二个过程做竖直上抛运动至最高点,对第一个过程,自制火箭做匀加速运动有
解得
a=20m/s2
由速度公式得
v1=at1=20×2m/s=40m/s
方向竖直向上;
(2)对第二个过程,由位移与速度关系公式得
代入数据解得
h2=80m
所以火箭上升离地面的最大高度
h=h1+h2=40m+80m=120m
(3)从燃料用完到运动至最高点的过程中,有
v1=gt2
解得
从最高点落回地面的过程中
解得
故总时间为
答:(1)燃料恰好用完时火箭的速度为40m/s,方向竖直向上;
(2)火箭上升离地面的最大高度为120m;
(3)火箭从发射到残骸落回地面过程的总时间为。
【点评】本题关键掌握火箭运动过程的分析和匀变速直线运动规律的使用。
12.(2024 西湖区校级期末)某同学将一橡皮球从离地高为H处由静止释放,落地后橡皮球第一次反弹高度为h=0.80m,已知橡皮球与地面第一次碰撞时间为t0=0.2s,碰撞前后速度大小之比为3:2,小球运动过程中所受空气阻力可忽略不计(重力加速度g取10m/s2),试求:
(1)橡皮球与地面第一次碰撞前的速度及释放时离地的高度H;
(2)橡皮球从释放至第一次反弹最高处所用时间。
【考点】竖直上抛运动的规律及应用;自由落体运动的规律及应用.
【专题】计算题;学科综合题;定量思想;方程法;自由落体运动专题;推理能力.
【答案】(1)橡皮球与地面第一次碰撞前的速度为6m/s,释放时离地的高度H为1.8m;
(2)橡皮球从释放至第一次反弹最高处所用时间为1.2s。
【分析】(1)根据速度—位移公式求出橡皮球与地面第一次碰撞前的速度,根据速度关系求出碰撞前的速度,然后求出释放时离地的高度H;
(2)根据速度—时间公式求出上升的时间与下落的时间,然后求和。
【解答】解:(1)设橡皮球与地面碰撞前、后的速度大小分别为v1,v2;碰撞后橡皮球上升过程,有
代入数据得:v2=4m/s
橡皮球碰撞前后v1:v2=3:2
联立解得v1=6m/s
橡皮球自由下落过程,有
得:H=1.8m
(2)橡皮球下落过程有v1=gt1
橡皮球反弹过程有v2=gt2
橡皮球从释放至反弹最高处所用时间为Δt=t1+t0+t2
联立解得Δt=1.2s
答:(1)橡皮球与地面第一次碰撞前的速度为6m/s,释放时离地的高度H为1.8m;
(2)橡皮球从释放至第一次反弹最高处所用时间为1.2s。
【点评】本题考查了自由落体运动和竖直上抛运动,要抓住竖直上抛运动的对称性来解题;小球每次与地面发生碰撞前后的速度大小之比是解题关键所在。
13.(2024 琼山区校级模拟)质量为m的小球以速度v0由水平地面竖直向上抛出,经多次与地面碰撞后,最终静止在地面上。已知小球与地面的碰撞为弹性碰撞,重力加速度记为g,运动过程中小球所受空气阻力视为恒定,大小为0.6mg。求小球
(1)从抛出到静止所经历的总路程;
(2)向上运动与向下运动的时间之比。
【考点】竖直上抛运动的规律及应用.
【专题】定量思想;推理法;直线运动规律专题;推理能力.
【答案】(1)从抛出到静止所经历的总路程为;
(2)向上运动与向下运动的时间之比为1:2。
【分析】(1)可利用动能定理计算位移;
(2)小球上升过程做匀减速直线运动,上升到最高点开始向下做匀加速直线运动,可分别计算利用牛顿第二定律计算加速度,利用加速度定义式分别计算向上运动的时间和向下运动的时间,进而计算比值。
【解答】解:(1)由于小球与地面发生弹性碰撞,没有机械能损失,由初状态到末状态由动能定理得
整理解得:
(2)上升过程由牛顿第二定律可知加速度为
整理解得a1=1.6g
下降过程由牛顿第二定律可知加速度为
上升和下降阶段速度的位移大小相等,则有
a上t上2a下t下2
整理解得t上:t下=1:2。
答:(1)从抛出到静止所经历的总路程为;
(2)向上运动与向下运动的时间之比为1:2。
【点评】本题考查了对竖直上抛运动的理解,其中旨在考查对匀变速直线运动规律的理解。
14.(2024 碑林区校级期末)节日里放的起花最早出自《儒林外史》,描述“形如小纸炮,缀有长约二三尺苇杆,燃其芯即急起”。设起花从地面发射后始终在竖直方向上运动,点火后可认为做初速度为0、加速度a=8m/s2的匀加速直线运动,当到达离地面高h=25m时燃料恰好用完。若不计空气阻力、忽略重力的变化,重力加速度g=10m/s2,求:
(1)起花上升的最大高度H;
(2)起花返回地面时的速度v;
(3)起花在空中运动的总时间t。
【考点】竖直上抛运动的规律及应用;匀变速直线运动规律的综合应用;匀变速直线运动位移与时间的关系.
【专题】计算题;定量思想;推理法;直线运动规律专题;推理能力.
【答案】见试题解答内容
【分析】(1)起花先向上做匀加速直线运动,后向上做匀减速直线运动,根据匀变速直线运动位移—速度公式列式求解两段高度,两高度之和即为上升的最大高度;
(2)起花下落过程做自由落体运动,根据自由落体运动位移—速度公式列式求解即可;
(3)根据速度—时间公式求解上升过程的时间,根据位移—时间公式求解下落过程的时间,三段时间之和即为在空中运动的总时间。
【解答】解:(1)设燃料用完时速度为v1,有:
设之后上升的高度为Δh,有:
代入数据联立解得:Δh=20m
起花上升的最大高度为:h+Δh=25m+20m=45m
(2)下落过程,根据自由落体运动位移—速度公式得:v2=2gH
代入数据解得:v=30m/s
(3)设起花加速上升的时间为t1,减速上升的时间为t2,自由下落的时间为t3,加速上升过程:v1=at1
减速上升过程:0=v1﹣gt2
下落过程:H
起花在空中运动的总时间为:t=t1+t2+t3
代入数据联立解得:t=7.5s
答:(1)起花上升的最大高度H为45m;
(2)起花返回地面时的速度v为30m/s;
(3)起花在空中运动的总时间t为7.5s。
【点评】本题考查匀变速直线运动,解题关键是分析好起花的运动过程,掌握匀变速直线运动的规律并能够熟练应用。
15.(2024 琼山区校级模拟)小敏在学过自由落体运动规律后,对自家房上下落的雨滴产生了兴趣,她坐在窗前发现从屋檐每隔相等时间滴下一滴水,当第5滴正欲滴下时,第1滴刚好落到地面,而第3滴与第2滴分别位于高1m的窗子的上、下沿。小敏同学在自己的作业本上画出了如图所示的雨滴下落同自家房子的关系,其中2点和3点之间的小矩形表示小敏正对的窗子(g取10m/s2),求:
(1)滴水的时间间隔。
(2)此屋檐离地面多高。
【考点】自由落体运动的规律及应用.
【专题】定量思想;比例法;自由落体运动专题;理解能力;推理能力.
【答案】(1)滴水的时间间隔为0.2s;
(2)此屋檐离地面3.2m
【分析】(2)由初速度等于零的匀加速直线运动的规律解答;(1)由自由落体规律计算雨滴下落时间,再定滴水间隔。
【解答】解:(2)由初速度等于零的匀加速直线运动的规律:相邻相同时间间隔内位移比为1:3:5:7: :(2n﹣1),得屋檐离地高度:H3.2m,(1)由自由落体规律:H 得:t,所以滴水时间间隔为:t′
答:(1)滴水的时间间隔为0.2s;
(2)此屋檐离地面3.2m
【点评】熟记初速度等于零的匀加速直线运动的各种推论,提高解题效率。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
