13.3.2 三角形的外角 同步练习(含答案)
文档属性
| 名称 | 13.3.2 三角形的外角 同步练习(含答案) | 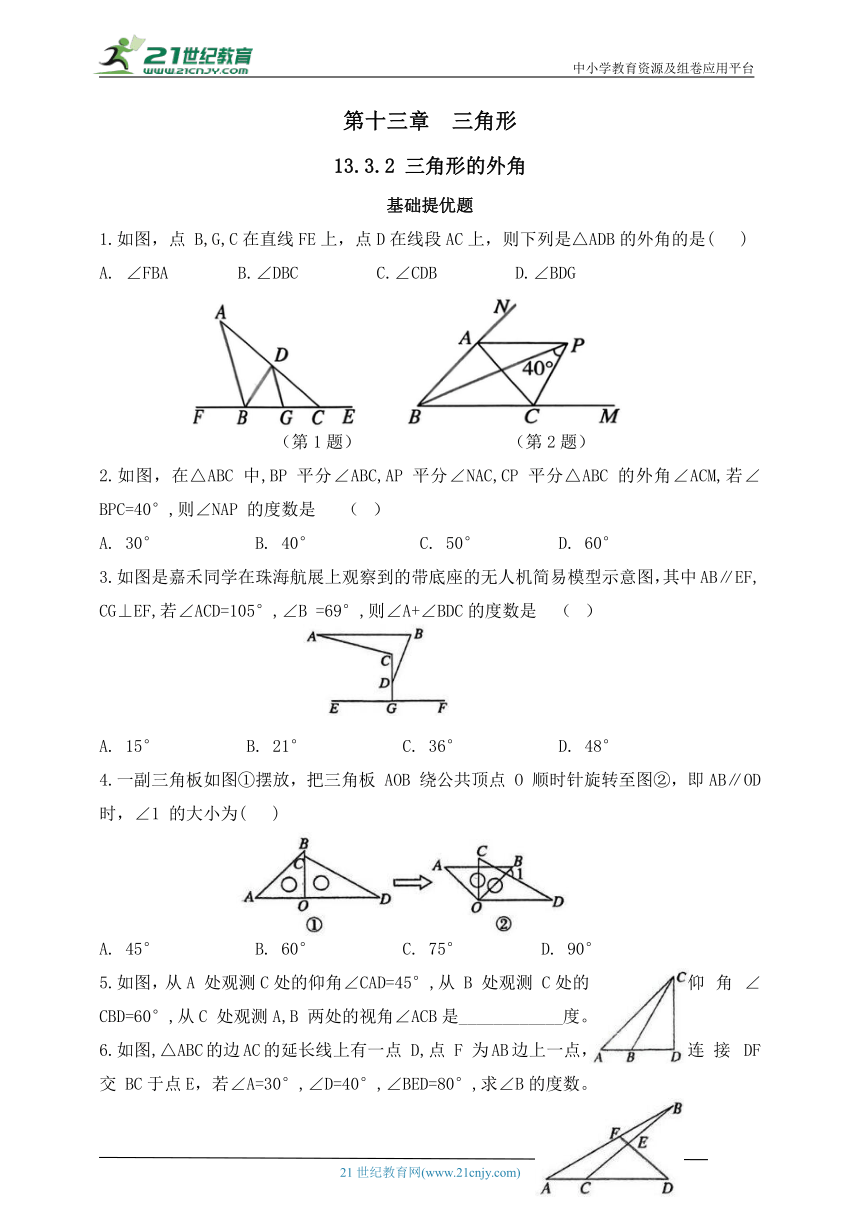 | |
| 格式 | docx | ||
| 文件大小 | 680.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 20:12:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十三章 三角形
13.3.2 三角形的外角
基础提优题
1.如图,点 B,G,C在直线FE上,点D在线段AC上,则下列是△ADB的外角的是( )
A. ∠FBA B.∠DBC C.∠CDB D.∠BDG
(第1题) (第2题)
2.如图,在△ABC 中,BP 平分∠ABC,AP 平分∠NAC,CP 平分△ABC 的外角∠ACM,若∠BPC=40°,则∠NAP 的度数是 ( )
A. 30° B. 40° C. 50° D. 60°
3.如图是嘉禾同学在珠海航展上观察到的带底座的无人机简易模型示意图,其中AB∥EF, CG⊥EF,若∠ACD=105°,∠B =69°,则∠A+∠BDC的度数是 ( )
A. 15° B. 21° C. 36° D. 48°
4.一副三角板如图①摆放,把三角板 AOB 绕公共顶点 O 顺时针旋转至图②,即AB∥OD时,∠1 的大小为( )
A. 45° B. 60° C. 75° D. 90°
5.如图,从A 处观测C处的仰角∠CAD=45°,从 B 处观测 C处的仰角∠CBD=60°,从C 处观测A,B 两处的视角∠ACB是____________度。
6.如图,△ABC的边AC的延长线上有一点 D,点 F 为AB边上一点,连接DF 交 BC于点E,若∠A=30°,∠D=40°,∠BED=80°,求∠B的度数。
综合应用题
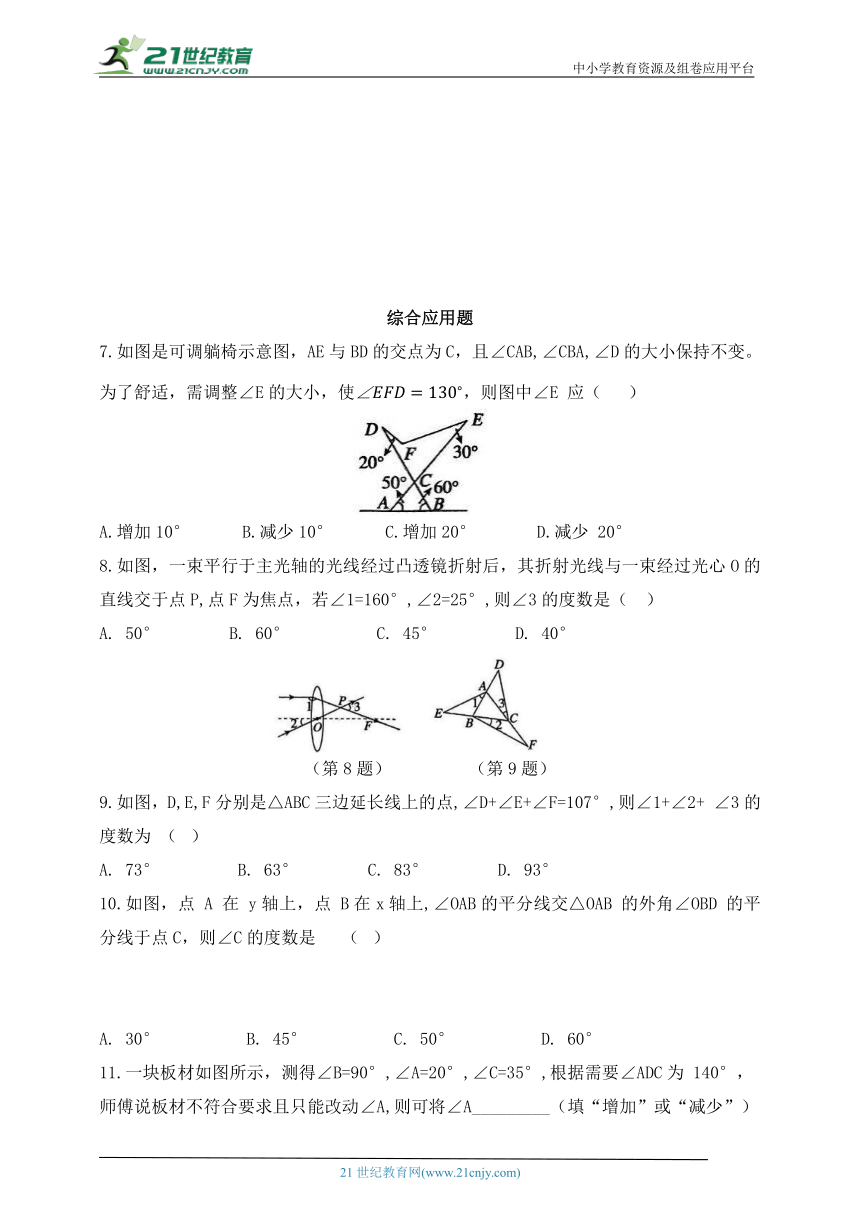
7.如图是可调躺椅示意图,AE与BD的交点为C,且∠CAB,∠CBA,∠D的大小保持不变。为了舒适,需调整∠E的大小,使,则图中∠E 应( )
A.增加10° B.减少10° C.增加20° D.减少 20°
8.如图,一束平行于主光轴的光线经过凸透镜折射后,其折射光线与一束经过光心O的直线交于点P,点F为焦点,若∠1=160°,∠2=25°,则∠3的度数是( )
A. 50° B. 60° C. 45° D. 40°
(第8题) (第9题)
9.如图,D,E,F分别是△ABC三边延长线上的点,∠D+∠E+∠F=107°,则∠1+∠2+ ∠3的度数为 ( )
A. 73° B. 63° C. 83° D. 93°
10.如图,点 A 在 y轴上,点 B在x轴上,∠OAB的平分线交△OAB 的外角∠OBD 的平分线于点C,则∠C的度数是 ( )
A. 30° B. 45° C. 50° D. 60°
11.一块板材如图所示,测得∠B=90°,∠A=20°,∠C=35°,根据需要∠ADC为 140°,师傅说板材不符合要求且只能改动∠A,则可将∠A_________(填“增加”或“减少”)__________°。
(第11题) (第12题)
12.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为___________。
13.如图,在 Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线 BE 交AC的延长线于点 E.
(1)求∠CBE的度数;
(2)过点 D 作DF∥BE,交AC的延长线于点 F,求∠F的度数。
创新拓展题
14.【概念认识】如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则 BD,BE叫作∠ABC的“三分线”,其中,BD 是“邻AB三分线”,BE是“邻BC三分线”。
(1)【问题解决】如图②,在△ABC中,∠A=70°,∠B=45°,若∠B 的三分线 BD 交AC 于点D,则∠BDC=__________ .
(2)如图③,在△ABC中,BP,CP 分别是∠ABC的“邻AB三分线”和∠ACB 的“邻 AC 三分线”,且BP⊥CP,求∠A 的度数。
(3)【延伸推广】在△ABC 中,∠ACD 是△ABC的外角,∠ABC 的三分线所在的直线与∠ACD 的三分线所在的直线交于点 P.若∠A=m°,∠ABC= n°,请画出图形,并求∠BPC的度数(用含 n,m的代数式表示)。
参考答案
1. C 2. C 3. C 4. C 5.15
6.【解】∵∠A=30°,∠D=40°,∠BFD 是△ADF的外角,∴∠BFD=∠A+∠D=70°.
又∵∠BED=80°,∠BED是△BEF的外角,∴∠B=∠BED-∠BFD=10°.
7. A 【点拨】延长EF交CD于点 G,如图,
∵∠CAB = 50°,∠CBA = 60°,
∴∠ECG=∠ACB=70°,∴∠DGF=∠E+∠ECG=∠E+70°.
∵∠D+∠DGF=∠EFD,∴20°+∠E+70°=130°,∴∠E=40°,
∴∠E增加40°-30°= 10°.
8. C 【点拨】如图.∵AB∥OF,∠1=160°,∴∠4+∠1=180°,
∴ ∠4= 180°-∠1= 20°.
∵∠POF=∠2=25°,∴∠3=
故选 C.
9. A
10. B 【点拨】∵∠OAB 的平分线交△OAB 的外角∠OBD的平分线于点C,
∴∠OAB= 2∠BAC,∠OBD= 2∠CBD.
∵∠OBD =∠OAB+∠AOB,∠CBD=∠BAC+∠C,
∴∠OAB+∠AOB=2∠CBD=2∠BAC+2∠C,∴∠AOB=2∠C.
∵∠AOB=90°,∴∠C=45°.
11.减少;5【点拨】如图,延长CD交AB于点 E.
∵∠ADC= ∠A+∠CEA,∠CEA=∠B+∠C,
∴∠ADC= ∠A+∠B +∠C =
∵根据需要∠ADC为140°,∴可将∠A减少5°.
点方法 求角的度数时,常通过构造三角形的外角,利用外角的性质解决.
12.360°【点拨】如图,
∠HGK+∠KHG+∠GKH=180°,∠AKH=∠A+∠B=∠HGK+∠KHG,∠CGK=∠C+∠D= ∠GKH+∠KHG,∠FHB=∠E+∠F=∠HKG+∠KGH,
∴∠A+∠B+∠C+∠D+∠E+∠F=2(∠HGK+∠KHG+∠GKH)=2×180°=360°.
13.【解】(1)∵∠ACB=90°,∠A=40°,∴∠CBD=130°.
∵BE是∠CBD的平分线,
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°,
14.【解】(1)85°或100°
(2)∵BP⊥CP,∴∠BPC=90°,∴∠PBC+∠PCB=90°.
又∵BP,CP 分别是∠ABC 的“邻 AB 三分线”和∠ACB的“邻 AC 三分线”,
,
∴∠ABC+∠ACB=135°.∴∠A = 180°-(∠ABC+∠ACB) = 45°
(3)分四种情况:
①如图①,当BP和CP分别是“邻AB 三分线”和“邻AC三分线”时,
②如图②,当 BP 和 CP 分别是“邻 BC三分线”和“邻CD三分线”时,
③如图③,当 BP 和 CP 分别是“邻BC三分线”和“邻AC三分线”时,
④如图④⑤,当 BP 和CP 分别是“邻AB 三分线”和“邻CD三分线”时,
当m>n时, ;
当m<n时,∠P=∠ABC-∠A=n°-m°.
综上所述,∠BPC的度数为或或或或n°-m°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十三章 三角形
13.3.2 三角形的外角
基础提优题
1.如图,点 B,G,C在直线FE上,点D在线段AC上,则下列是△ADB的外角的是( )
A. ∠FBA B.∠DBC C.∠CDB D.∠BDG
(第1题) (第2题)
2.如图,在△ABC 中,BP 平分∠ABC,AP 平分∠NAC,CP 平分△ABC 的外角∠ACM,若∠BPC=40°,则∠NAP 的度数是 ( )
A. 30° B. 40° C. 50° D. 60°
3.如图是嘉禾同学在珠海航展上观察到的带底座的无人机简易模型示意图,其中AB∥EF, CG⊥EF,若∠ACD=105°,∠B =69°,则∠A+∠BDC的度数是 ( )
A. 15° B. 21° C. 36° D. 48°
4.一副三角板如图①摆放,把三角板 AOB 绕公共顶点 O 顺时针旋转至图②,即AB∥OD时,∠1 的大小为( )
A. 45° B. 60° C. 75° D. 90°
5.如图,从A 处观测C处的仰角∠CAD=45°,从 B 处观测 C处的仰角∠CBD=60°,从C 处观测A,B 两处的视角∠ACB是____________度。
6.如图,△ABC的边AC的延长线上有一点 D,点 F 为AB边上一点,连接DF 交 BC于点E,若∠A=30°,∠D=40°,∠BED=80°,求∠B的度数。
综合应用题
7.如图是可调躺椅示意图,AE与BD的交点为C,且∠CAB,∠CBA,∠D的大小保持不变。为了舒适,需调整∠E的大小,使,则图中∠E 应( )
A.增加10° B.减少10° C.增加20° D.减少 20°
8.如图,一束平行于主光轴的光线经过凸透镜折射后,其折射光线与一束经过光心O的直线交于点P,点F为焦点,若∠1=160°,∠2=25°,则∠3的度数是( )
A. 50° B. 60° C. 45° D. 40°
(第8题) (第9题)
9.如图,D,E,F分别是△ABC三边延长线上的点,∠D+∠E+∠F=107°,则∠1+∠2+ ∠3的度数为 ( )
A. 73° B. 63° C. 83° D. 93°
10.如图,点 A 在 y轴上,点 B在x轴上,∠OAB的平分线交△OAB 的外角∠OBD 的平分线于点C,则∠C的度数是 ( )
A. 30° B. 45° C. 50° D. 60°
11.一块板材如图所示,测得∠B=90°,∠A=20°,∠C=35°,根据需要∠ADC为 140°,师傅说板材不符合要求且只能改动∠A,则可将∠A_________(填“增加”或“减少”)__________°。
(第11题) (第12题)
12.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为___________。
13.如图,在 Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线 BE 交AC的延长线于点 E.
(1)求∠CBE的度数;
(2)过点 D 作DF∥BE,交AC的延长线于点 F,求∠F的度数。
创新拓展题
14.【概念认识】如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则 BD,BE叫作∠ABC的“三分线”,其中,BD 是“邻AB三分线”,BE是“邻BC三分线”。
(1)【问题解决】如图②,在△ABC中,∠A=70°,∠B=45°,若∠B 的三分线 BD 交AC 于点D,则∠BDC=__________ .
(2)如图③,在△ABC中,BP,CP 分别是∠ABC的“邻AB三分线”和∠ACB 的“邻 AC 三分线”,且BP⊥CP,求∠A 的度数。
(3)【延伸推广】在△ABC 中,∠ACD 是△ABC的外角,∠ABC 的三分线所在的直线与∠ACD 的三分线所在的直线交于点 P.若∠A=m°,∠ABC= n°,请画出图形,并求∠BPC的度数(用含 n,m的代数式表示)。
参考答案
1. C 2. C 3. C 4. C 5.15
6.【解】∵∠A=30°,∠D=40°,∠BFD 是△ADF的外角,∴∠BFD=∠A+∠D=70°.
又∵∠BED=80°,∠BED是△BEF的外角,∴∠B=∠BED-∠BFD=10°.
7. A 【点拨】延长EF交CD于点 G,如图,
∵∠CAB = 50°,∠CBA = 60°,
∴∠ECG=∠ACB=70°,∴∠DGF=∠E+∠ECG=∠E+70°.
∵∠D+∠DGF=∠EFD,∴20°+∠E+70°=130°,∴∠E=40°,
∴∠E增加40°-30°= 10°.
8. C 【点拨】如图.∵AB∥OF,∠1=160°,∴∠4+∠1=180°,
∴ ∠4= 180°-∠1= 20°.
∵∠POF=∠2=25°,∴∠3=
故选 C.
9. A
10. B 【点拨】∵∠OAB 的平分线交△OAB 的外角∠OBD的平分线于点C,
∴∠OAB= 2∠BAC,∠OBD= 2∠CBD.
∵∠OBD =∠OAB+∠AOB,∠CBD=∠BAC+∠C,
∴∠OAB+∠AOB=2∠CBD=2∠BAC+2∠C,∴∠AOB=2∠C.
∵∠AOB=90°,∴∠C=45°.
11.减少;5【点拨】如图,延长CD交AB于点 E.
∵∠ADC= ∠A+∠CEA,∠CEA=∠B+∠C,
∴∠ADC= ∠A+∠B +∠C =
∵根据需要∠ADC为140°,∴可将∠A减少5°.
点方法 求角的度数时,常通过构造三角形的外角,利用外角的性质解决.
12.360°【点拨】如图,
∠HGK+∠KHG+∠GKH=180°,∠AKH=∠A+∠B=∠HGK+∠KHG,∠CGK=∠C+∠D= ∠GKH+∠KHG,∠FHB=∠E+∠F=∠HKG+∠KGH,
∴∠A+∠B+∠C+∠D+∠E+∠F=2(∠HGK+∠KHG+∠GKH)=2×180°=360°.
13.【解】(1)∵∠ACB=90°,∠A=40°,∴∠CBD=130°.
∵BE是∠CBD的平分线,
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.
∵DF∥BE,∴∠F=∠CEB=25°,
14.【解】(1)85°或100°
(2)∵BP⊥CP,∴∠BPC=90°,∴∠PBC+∠PCB=90°.
又∵BP,CP 分别是∠ABC 的“邻 AB 三分线”和∠ACB的“邻 AC 三分线”,
,
∴∠ABC+∠ACB=135°.∴∠A = 180°-(∠ABC+∠ACB) = 45°
(3)分四种情况:
①如图①,当BP和CP分别是“邻AB 三分线”和“邻AC三分线”时,
②如图②,当 BP 和 CP 分别是“邻 BC三分线”和“邻CD三分线”时,
③如图③,当 BP 和 CP 分别是“邻BC三分线”和“邻AC三分线”时,
④如图④⑤,当 BP 和CP 分别是“邻AB 三分线”和“邻CD三分线”时,
当m>n时, ;
当m<n时,∠P=∠ABC-∠A=n°-m°.
综上所述,∠BPC的度数为或或或或n°-m°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
