第十三章 三角形 专题2 三角形中角的经典模型(含答案)
文档属性
| 名称 | 第十三章 三角形 专题2 三角形中角的经典模型(含答案) | 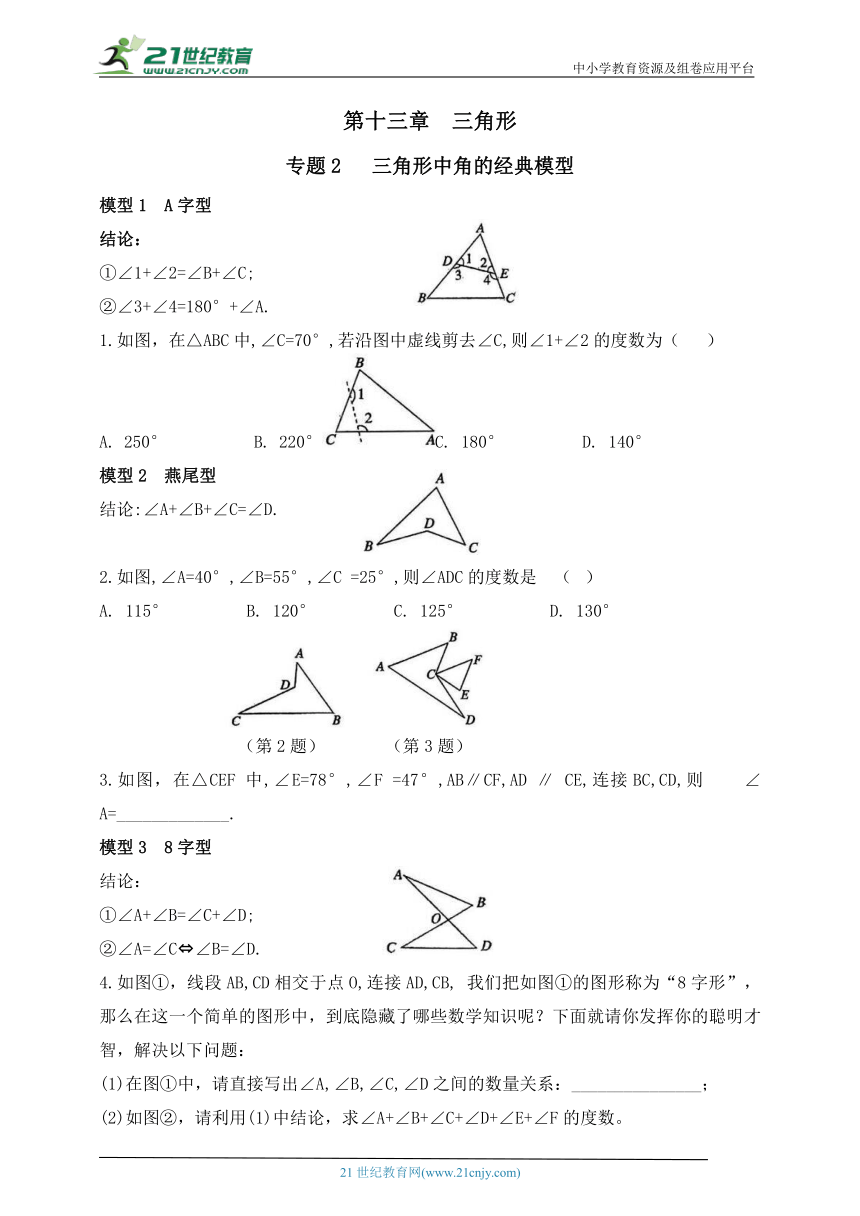 | |
| 格式 | docx | ||
| 文件大小 | 723.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 20:16:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十三章 三角形
专题2 三角形中角的经典模型
模型1 A字型
结论:
①∠1+∠2=∠B+∠C;
②∠3+∠4=180°+∠A.
1.如图,在△ABC中,∠C=70°,若沿图中虚线剪去∠C,则∠1+∠2的度数为( )
A. 250° B. 220° C. 180° D. 140°
模型2 燕尾型
结论:∠A+∠B+∠C=∠D.
2.如图,∠A=40°,∠B=55°,∠C =25°,则∠ADC的度数是 ( )
A. 115° B. 120° C. 125° D. 130°
(第2题) (第3题)
3.如图,在△CEF 中,∠E=78°,∠F =47°,AB∥CF,AD ∥ CE,连接BC,CD,则 ∠A=_____________.
模型3 8字型
结论:
①∠A+∠B=∠C+∠D;
②∠A=∠C ∠B=∠D.
4.如图①,线段AB,CD相交于点O,连接AD,CB, 我们把如图①的图形称为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图①中,请直接写出∠A,∠B,∠C,∠D之间的数量关系:_______________;
(2)如图②,请利用(1)中结论,求∠A+∠B+∠C+∠D+∠E+∠F的度数。
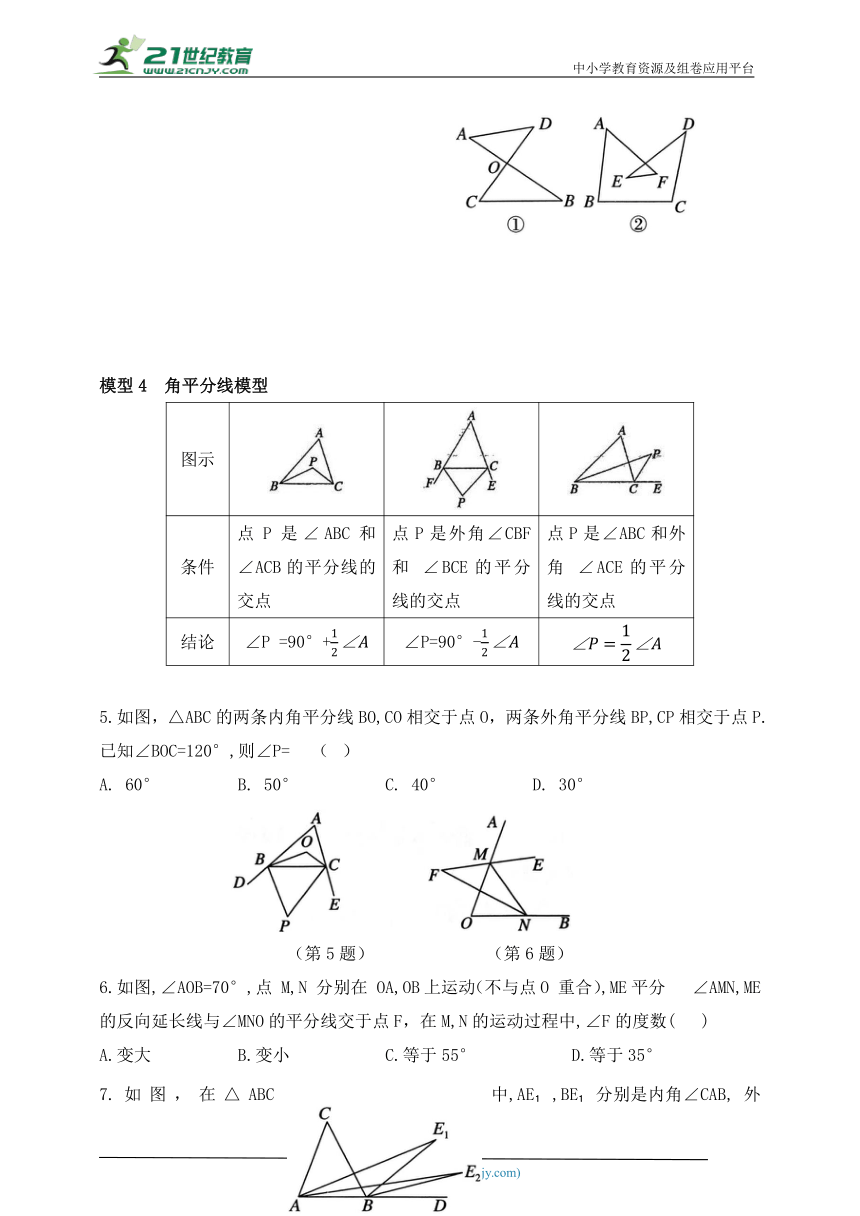
模型4 角平分线模型
图示
条件 点P是∠ABC和 ∠ACB的平分线的交点 点P是外角∠CBF和 ∠BCE的平分线的交点 点P是∠ABC和外角 ∠ACE的平分线的交点
结论 ∠P =90°+ ∠P=90°-
5.如图,△ABC的两条内角平分线BO,CO相交于点O,两条外角平分线BP,CP相交于点P.已知∠BOC=120°,则∠P= ( )
A. 60° B. 50° C. 40° D. 30°
(第5题) (第6题)
6.如图,∠AOB=70°,点 M,N 分别在 OA,OB上运动(不与点O 重合),ME平分 ∠AMN,ME 的反向延长线与∠MNO的平分线交于点F,在M,N的运动过程中,∠F的度数( )
A.变大 B.变小 C.等于55° D.等于35°
7.如图,在△ABC 中,AE ,BE 分别是内角∠CAB, 外角∠CBD 的三等分线,且 , ,在△ABE 中,AE ,BE 分别是内角 ∠E AB,外角∠E BD的三等分线,且,, ,以此规律作下去,若 ,则 ∠En =____________度。
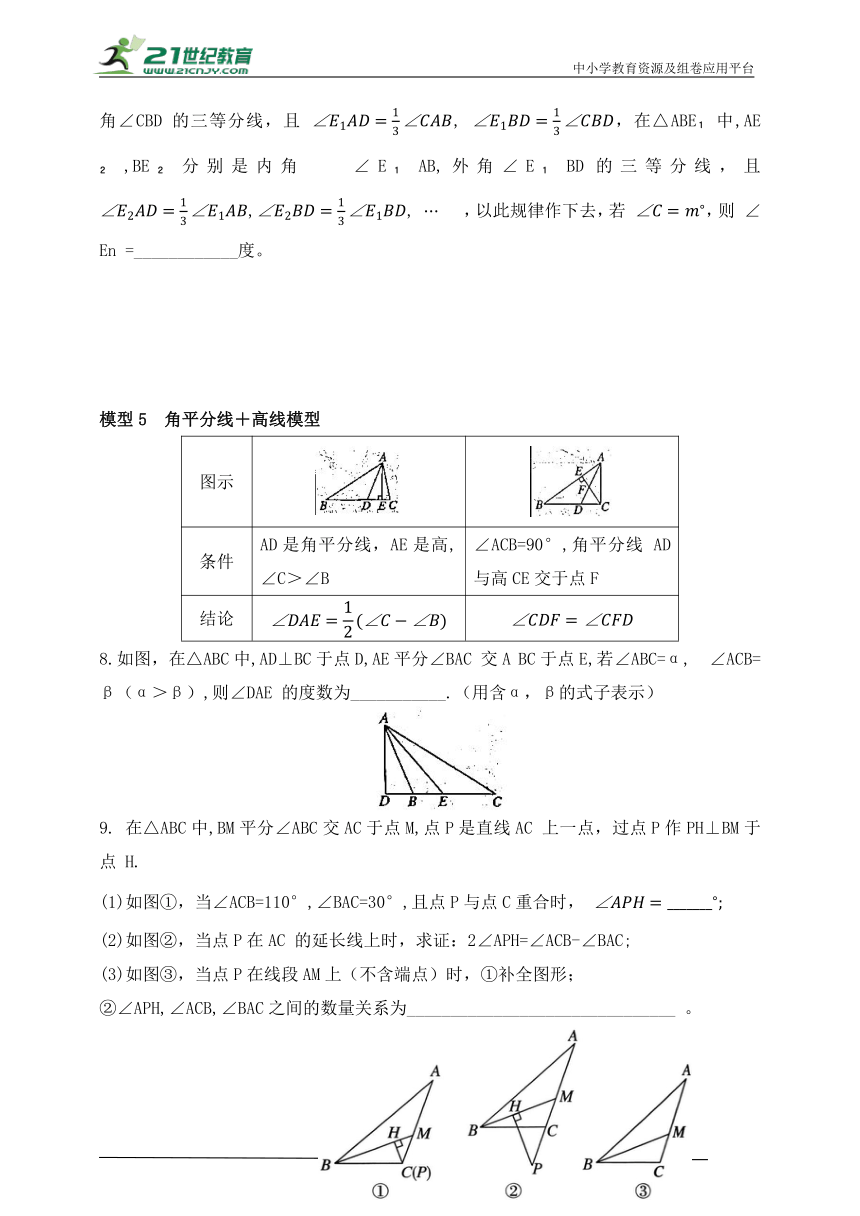
模型5 角平分线+高线模型
图示
条件 AD是角平分线,AE是高,∠C>∠B ∠ACB=90°,角平分线 AD 与高CE交于点F
结论
8.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC 交A BC于点E,若∠ABC=α, ∠ACB=β(α>β),则∠DAE 的度数为___________.(用含α,β的式子表示)
9. 在△ABC中,BM平分∠ABC交AC于点M,点P是直线AC 上一点,过点P作PH⊥BM于点 H.
(1)如图①,当∠ACB=110°,∠BAC=30°,且点P与点C重合时,
(2)如图②,当点P在AC 的延长线上时,求证:2∠APH=∠ACB-∠BAC;
(3)如图③,当点P在线段AM上(不含端点)时,①补全图形;
②∠APH,∠ACB,∠BAC之间的数量关系为_______________________________ 。
参考答案
1、A
2、B 【点拨】延长AD交BC 于点E,如图.
∵∠ADC是△CDE的一个外角,∴∠ADC=∠C+∠CED.
∵∠CED是△ABE的一个外角,∴∠CED=∠A+∠B,
∴∠ADC=∠C+∠A+∠B=故选B、
3、55°【点拨】延长EC交于点H,如图.
∵∠E=78°,∠F=47°,∴∠ECF=180°-∠E-∠F=55°.
∵AB∥CF,AD∥CE,∴∠BHE=∠ECF=55°,∠BHE =∠A,∴∠A=55°.
4.【解】(1)∠A+∠D=∠B+∠C
(2)如图,连接AD,则∠BAD+∠B+∠C+∠ADC=360°.
根据(1)中的结论可得∠E+∠F=∠BAD+∠FAD,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°.
5. A【点读】∵∠BOC=120°,∴∠OBC+∠OCB=180°-∠BOC=60°.
又∵BO,CO是∠ABC,∠ACB的平分线,∴∠ABC+∠ACB =2(∠OBC+∠OCB) =120°,
∴∠CBD+∠BCE=360°-(∠ABC+∠ACB)=240°.
∵BP,CP是∠CBD,∠BCE 的平分线,∴∠CBP+ , (∠CBP+∠BCP)=60°.
6. D 【点缀】∵ME平分∠AMN, NF平分∠MNO,
,
∵∠AMN,
, ∠MNF.
根据外角的定义,得∠EMN=∠F+∠MNF,∴∠F=85°.
【点拨】设∠E AD=α,∠E1BD=β.
∵∠E AD= , , ∠
, ,∴
同理可求, ,,即
【点拨】∵∠ABC=α,∠C=β,∴∠BAC=180°-∠B-∠C=180°-α-β.
∵AE平分∠BAC交BC于点E..,
∵AD⊥
9.(1)40【点拨】∵∠ACB =110°,∠BAC=30°,
∴∠ABC=180°-∠BAC-∠BCA=180°-30°-110°=40°,
∵BM平分∠ABC,∴∠HBC=∠ABC=
∵PH⊥BM,∴∠HCB=90°-∠HBC=90°-20°=70°,
∴∠APH=∠ACB-∠HCB=110°-70°=40°.
(2)【证明】如图①,作射线AH,则可得∠4=∠1+∠2,∠3=∠5+∠P,
∴∠3+∠4=∠1+∠2+∠5+∠P.
∵PH⊥BH,∴∠3+∠4=90°,即∠BAC+∠2+∠P=90°,
∴∠P=90°-∠BAC-∠2.
∵BH平分∠ABC,∴∠2=∠ABC.
∵∠ABC+∠BAC+∠ACB=180°,∴∠ABC=180°-∠BAC-∠ACB,
∴∠2=
∴2∠APH=180°-∠ACB-∠BAC.
(3)【解】①如图②.
②∠APH=180°+
【点拨】∵BH平分∠ABC,∴∠ABH=∠ABC=(180°-∠BAC-∠ACB).
∵PH⊥BH,∴∠APH=90°+∠AMH=90°+(∠ABH+∠BAC)=90°+(180°- ∠BAC-∠ACB)+∠BAC=180°+(∠BAC-∠ACB),
即∠APH=180°+ (∠BAC-∠ACB).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十三章 三角形
专题2 三角形中角的经典模型
模型1 A字型
结论:
①∠1+∠2=∠B+∠C;
②∠3+∠4=180°+∠A.
1.如图,在△ABC中,∠C=70°,若沿图中虚线剪去∠C,则∠1+∠2的度数为( )
A. 250° B. 220° C. 180° D. 140°
模型2 燕尾型
结论:∠A+∠B+∠C=∠D.
2.如图,∠A=40°,∠B=55°,∠C =25°,则∠ADC的度数是 ( )
A. 115° B. 120° C. 125° D. 130°
(第2题) (第3题)
3.如图,在△CEF 中,∠E=78°,∠F =47°,AB∥CF,AD ∥ CE,连接BC,CD,则 ∠A=_____________.
模型3 8字型
结论:
①∠A+∠B=∠C+∠D;
②∠A=∠C ∠B=∠D.
4.如图①,线段AB,CD相交于点O,连接AD,CB, 我们把如图①的图形称为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图①中,请直接写出∠A,∠B,∠C,∠D之间的数量关系:_______________;
(2)如图②,请利用(1)中结论,求∠A+∠B+∠C+∠D+∠E+∠F的度数。
模型4 角平分线模型
图示
条件 点P是∠ABC和 ∠ACB的平分线的交点 点P是外角∠CBF和 ∠BCE的平分线的交点 点P是∠ABC和外角 ∠ACE的平分线的交点
结论 ∠P =90°+ ∠P=90°-
5.如图,△ABC的两条内角平分线BO,CO相交于点O,两条外角平分线BP,CP相交于点P.已知∠BOC=120°,则∠P= ( )
A. 60° B. 50° C. 40° D. 30°
(第5题) (第6题)
6.如图,∠AOB=70°,点 M,N 分别在 OA,OB上运动(不与点O 重合),ME平分 ∠AMN,ME 的反向延长线与∠MNO的平分线交于点F,在M,N的运动过程中,∠F的度数( )
A.变大 B.变小 C.等于55° D.等于35°
7.如图,在△ABC 中,AE ,BE 分别是内角∠CAB, 外角∠CBD 的三等分线,且 , ,在△ABE 中,AE ,BE 分别是内角 ∠E AB,外角∠E BD的三等分线,且,, ,以此规律作下去,若 ,则 ∠En =____________度。
模型5 角平分线+高线模型
图示
条件 AD是角平分线,AE是高,∠C>∠B ∠ACB=90°,角平分线 AD 与高CE交于点F
结论
8.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC 交A BC于点E,若∠ABC=α, ∠ACB=β(α>β),则∠DAE 的度数为___________.(用含α,β的式子表示)
9. 在△ABC中,BM平分∠ABC交AC于点M,点P是直线AC 上一点,过点P作PH⊥BM于点 H.
(1)如图①,当∠ACB=110°,∠BAC=30°,且点P与点C重合时,
(2)如图②,当点P在AC 的延长线上时,求证:2∠APH=∠ACB-∠BAC;
(3)如图③,当点P在线段AM上(不含端点)时,①补全图形;
②∠APH,∠ACB,∠BAC之间的数量关系为_______________________________ 。
参考答案
1、A
2、B 【点拨】延长AD交BC 于点E,如图.
∵∠ADC是△CDE的一个外角,∴∠ADC=∠C+∠CED.
∵∠CED是△ABE的一个外角,∴∠CED=∠A+∠B,
∴∠ADC=∠C+∠A+∠B=故选B、
3、55°【点拨】延长EC交于点H,如图.
∵∠E=78°,∠F=47°,∴∠ECF=180°-∠E-∠F=55°.
∵AB∥CF,AD∥CE,∴∠BHE=∠ECF=55°,∠BHE =∠A,∴∠A=55°.
4.【解】(1)∠A+∠D=∠B+∠C
(2)如图,连接AD,则∠BAD+∠B+∠C+∠ADC=360°.
根据(1)中的结论可得∠E+∠F=∠BAD+∠FAD,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°.
5. A【点读】∵∠BOC=120°,∴∠OBC+∠OCB=180°-∠BOC=60°.
又∵BO,CO是∠ABC,∠ACB的平分线,∴∠ABC+∠ACB =2(∠OBC+∠OCB) =120°,
∴∠CBD+∠BCE=360°-(∠ABC+∠ACB)=240°.
∵BP,CP是∠CBD,∠BCE 的平分线,∴∠CBP+ , (∠CBP+∠BCP)=60°.
6. D 【点缀】∵ME平分∠AMN, NF平分∠MNO,
,
∵∠AMN,
, ∠MNF.
根据外角的定义,得∠EMN=∠F+∠MNF,∴∠F=85°.
【点拨】设∠E AD=α,∠E1BD=β.
∵∠E AD= , , ∠
, ,∴
同理可求, ,,即
【点拨】∵∠ABC=α,∠C=β,∴∠BAC=180°-∠B-∠C=180°-α-β.
∵AE平分∠BAC交BC于点E..,
∵AD⊥
9.(1)40【点拨】∵∠ACB =110°,∠BAC=30°,
∴∠ABC=180°-∠BAC-∠BCA=180°-30°-110°=40°,
∵BM平分∠ABC,∴∠HBC=∠ABC=
∵PH⊥BM,∴∠HCB=90°-∠HBC=90°-20°=70°,
∴∠APH=∠ACB-∠HCB=110°-70°=40°.
(2)【证明】如图①,作射线AH,则可得∠4=∠1+∠2,∠3=∠5+∠P,
∴∠3+∠4=∠1+∠2+∠5+∠P.
∵PH⊥BH,∴∠3+∠4=90°,即∠BAC+∠2+∠P=90°,
∴∠P=90°-∠BAC-∠2.
∵BH平分∠ABC,∴∠2=∠ABC.
∵∠ABC+∠BAC+∠ACB=180°,∴∠ABC=180°-∠BAC-∠ACB,
∴∠2=
∴2∠APH=180°-∠ACB-∠BAC.
(3)【解】①如图②.
②∠APH=180°+
【点拨】∵BH平分∠ABC,∴∠ABH=∠ABC=(180°-∠BAC-∠ACB).
∵PH⊥BH,∴∠APH=90°+∠AMH=90°+(∠ABH+∠BAC)=90°+(180°- ∠BAC-∠ACB)+∠BAC=180°+(∠BAC-∠ACB),
即∠APH=180°+ (∠BAC-∠ACB).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
