第十三章 三角形 专题3 三角形的叠放、折叠问题(含答案)
文档属性
| 名称 | 第十三章 三角形 专题3 三角形的叠放、折叠问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 20:19:53 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十三章 三角形
专题3 三角形的叠放、折叠问题
类型1 三角形叠放问题
1.如图,将两块三角尺(∠A=60°,∠D=30°,∠E=∠B=45°)的直角顶点叠放在一起。当0°<∠ACE<180°且点E在直线AC的上方时,若这两块三角尺有一组边互相平行,求∠ACE 的度数。(画出符合条件的图形,并直接写出相应的∠ACE 的度数)
2.取一副三角尺按图①拼接,固定三角尺ADC,将三角尺 ABC 绕点 A 按顺时针方向旋转得到△ABC′,如图②所示。设∠CAC′=α.
(1)当α=15°时,求证:AB∥CD;
(2)连接 BD,当 时,的度数是否变化,若变化,求出变化范围;若不变,求出其度数。
类型2 三角形折叠问题
3.如图,把三角形纸片ABC沿着 DE 折叠。
(1)若点A落在四边形 BCDE 内部点A'的位置(如图①),且 , ,请求出∠A′的度数;
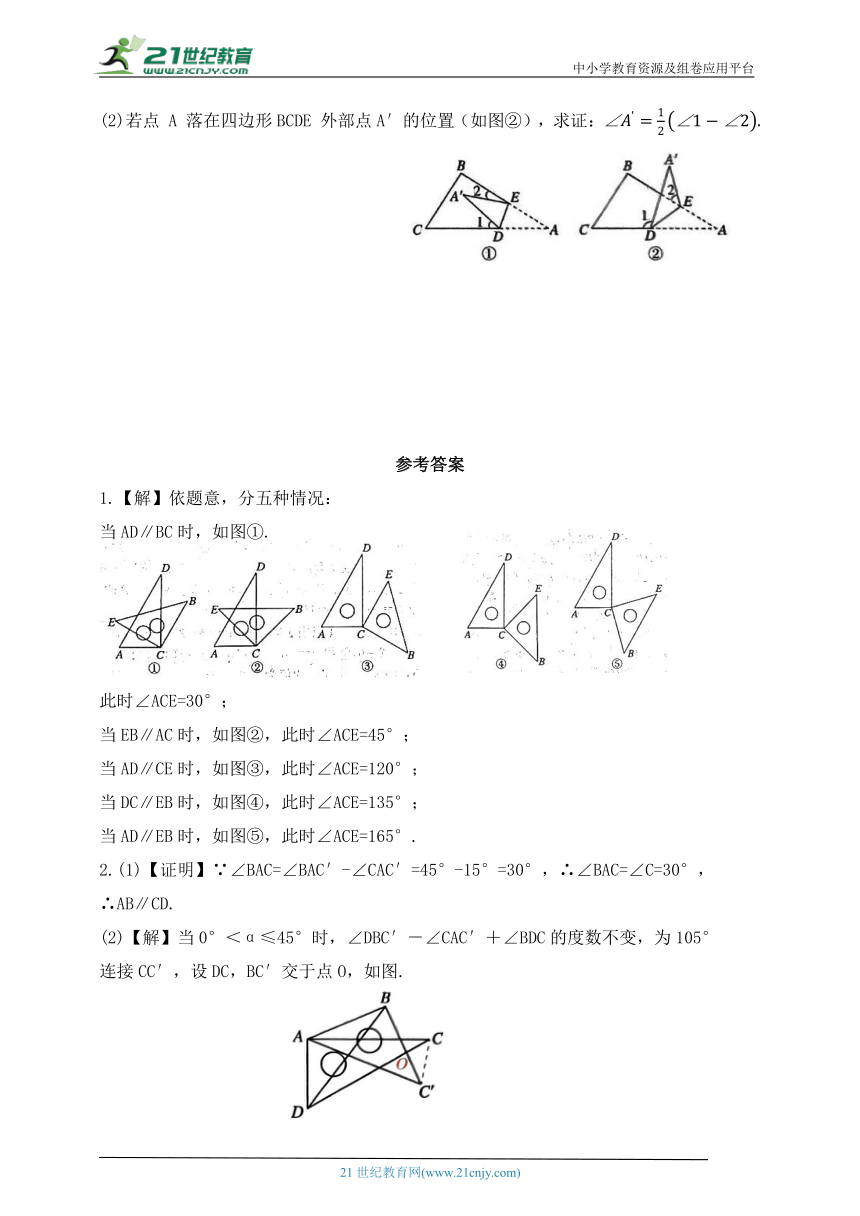
(2)若点 A 落在四边形BCDE 外部点A′的位置(如图②),求证:
参考答案
1.【解】依题意,分五种情况:
当AD∥BC时,如图①.
此时∠ACE=30°;
当EB∥AC时,如图②,此时∠ACE=45°;
当AD∥CE时,如图③,此时∠ACE=120°;
当DC∥EB时,如图④,此时∠ACE=135°;
当AD∥EB时,如图⑤,此时∠ACE=165°.
2.(1)【证明】∵∠BAC=∠BAC′-∠CAC′=45°-15°=30°,∴∠BAC=∠C=30°,
∴AB∥CD.
(2)【解】当0°<α≤45°时,∠DBC′-∠CAC′+∠BDC的度数不变,为105°
连接CC′,设DC,BC′交于点O,如图.
在△BDO和△OCC′中,∠BOD=∠COC′,∴∠BDO+∠DBO=∠OCC′+∠OC′C,
∴∠DBC′+∠CAC′+∠BDC=∠BDO+α+∠DBO-∠OCC′+∠OC′C+α=180°-45°-30°=105°,即当0°<α≤45°时,∠DBC′-∠CAC′+∠BDC的度数不变,为105°.
3.(1)【解】由折叠的性质得∠A=∠A′,∠ADE=∠A′DE,∠AED=∠A′ED.
∵∠1+∠ADE+∠A′DE=180°,∠1=40°,∠2+∠AED+∠A′ED=180°,∠2=24°,∴∠ADE=∠A′DE=70°,∠AED=∠A′ED=78°,∴∠A′=180°-∠A′DE-∠A′ED=32°.
(2)【证明】由折叠的性质得∠A=∠A′∠ADE=∠A′DE,∠AED=∠A′ED.
∵∠ADE+∠A′DE+∠1=180°,∴∠ADE=∠A′DE=
∴∠A′ED=∠AED=180°-∠A-∠ADE=180°-∠A-90°+=90°-∠A+,∴∠BED=180°-∠AED=90°+∠A-,∴∠2=∠A′ED-∠BED=90°-∠A+-(90°+∠A-)=∠1-2∠A=∠1-2∠A′,∴∠A′=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十三章 三角形
专题3 三角形的叠放、折叠问题
类型1 三角形叠放问题
1.如图,将两块三角尺(∠A=60°,∠D=30°,∠E=∠B=45°)的直角顶点叠放在一起。当0°<∠ACE<180°且点E在直线AC的上方时,若这两块三角尺有一组边互相平行,求∠ACE 的度数。(画出符合条件的图形,并直接写出相应的∠ACE 的度数)
2.取一副三角尺按图①拼接,固定三角尺ADC,将三角尺 ABC 绕点 A 按顺时针方向旋转得到△ABC′,如图②所示。设∠CAC′=α.
(1)当α=15°时,求证:AB∥CD;
(2)连接 BD,当 时,的度数是否变化,若变化,求出变化范围;若不变,求出其度数。
类型2 三角形折叠问题
3.如图,把三角形纸片ABC沿着 DE 折叠。
(1)若点A落在四边形 BCDE 内部点A'的位置(如图①),且 , ,请求出∠A′的度数;
(2)若点 A 落在四边形BCDE 外部点A′的位置(如图②),求证:
参考答案
1.【解】依题意,分五种情况:
当AD∥BC时,如图①.
此时∠ACE=30°;
当EB∥AC时,如图②,此时∠ACE=45°;
当AD∥CE时,如图③,此时∠ACE=120°;
当DC∥EB时,如图④,此时∠ACE=135°;
当AD∥EB时,如图⑤,此时∠ACE=165°.
2.(1)【证明】∵∠BAC=∠BAC′-∠CAC′=45°-15°=30°,∴∠BAC=∠C=30°,
∴AB∥CD.
(2)【解】当0°<α≤45°时,∠DBC′-∠CAC′+∠BDC的度数不变,为105°
连接CC′,设DC,BC′交于点O,如图.
在△BDO和△OCC′中,∠BOD=∠COC′,∴∠BDO+∠DBO=∠OCC′+∠OC′C,
∴∠DBC′+∠CAC′+∠BDC=∠BDO+α+∠DBO-∠OCC′+∠OC′C+α=180°-45°-30°=105°,即当0°<α≤45°时,∠DBC′-∠CAC′+∠BDC的度数不变,为105°.
3.(1)【解】由折叠的性质得∠A=∠A′,∠ADE=∠A′DE,∠AED=∠A′ED.
∵∠1+∠ADE+∠A′DE=180°,∠1=40°,∠2+∠AED+∠A′ED=180°,∠2=24°,∴∠ADE=∠A′DE=70°,∠AED=∠A′ED=78°,∴∠A′=180°-∠A′DE-∠A′ED=32°.
(2)【证明】由折叠的性质得∠A=∠A′∠ADE=∠A′DE,∠AED=∠A′ED.
∵∠ADE+∠A′DE+∠1=180°,∴∠ADE=∠A′DE=
∴∠A′ED=∠AED=180°-∠A-∠ADE=180°-∠A-90°+=90°-∠A+,∴∠BED=180°-∠AED=90°+∠A-,∴∠2=∠A′ED-∠BED=90°-∠A+-(90°+∠A-)=∠1-2∠A=∠1-2∠A′,∴∠A′=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
