13.2.1 三角形的边 同步练习(含答案)
文档属性
| 名称 | 13.2.1 三角形的边 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 659.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 20:27:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十三章 三角形
13.2 与三角形有关的线段
13.2.1 三角形的边
基础提优题目
1.满足下列条件的三条线段a,b,c,能组成三角形的有 ( )
A.①② B.③④ C.①④ D.①③
2.如图,人字梯的支架AB,AC的长度都为2m(连接处的长度忽略不计),则B,C两点之间的距离可能是 ( )
A. 3 m B. 4.2 m C. 5 m D. 6 m
3.若使用如图所示的①②两根铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以折成两段的铁丝是( )
A.只有①可以 B.只有②可以 C.①②都可以 D.①②都不可以
4.2024年10 月30日4时27分,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心点火发射。在发射运载火箭时,运载火箭的发射架被焊接成了许多的三角形,这样做的原因是:_________________________________.
5.已知△ABC的三边长为a,b,c,化简的结果是_____________。
6.学具盒中装有四根长度分别为1 cm,3 cm,4 cm和5 cm 的细木棒,小明手中有一根长度为3cm的细木棒,现从盒中取出两根细木棒与小明手中的细木棒放在一起组成三角形,可以组成__________种不同的三角形。
7.已知△ABC的三边长分别为4,9,x.
(1)求x的取值范围;
(2)若它是一个等腰三角形,求它的周长。
综合应用题
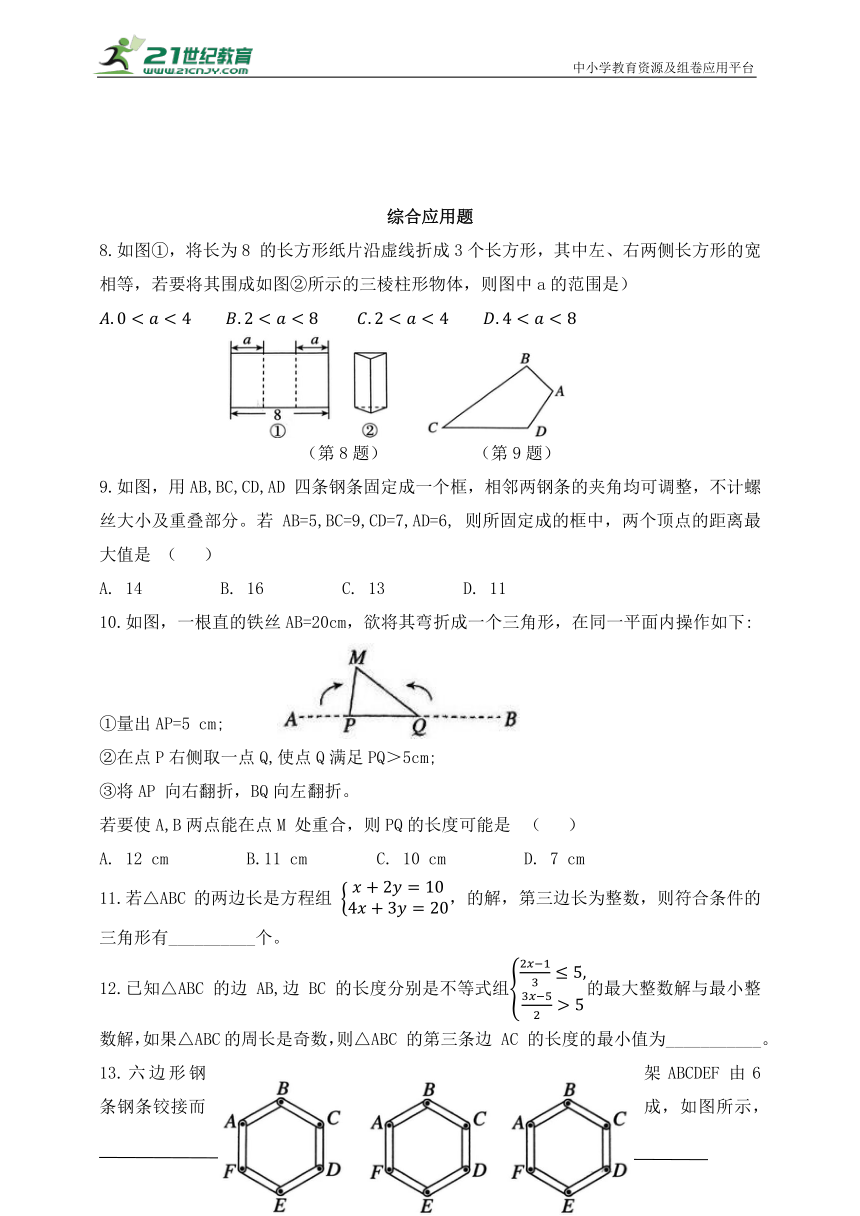
8.如图①,将长为8 的长方形纸片沿虚线折成3个长方形,其中左、右两侧长方形的宽相等,若要将其围成如图②所示的三棱柱形物体,则图中a的范围是)
(第8题) (第9题)
9.如图,用AB,BC,CD,AD 四条钢条固定成一个框,相邻两钢条的夹角均可调整,不计螺丝大小及重叠部分。若AB=5,BC=9,CD=7,AD=6, 则所固定成的框中,两个顶点的距离最大值是 ( )
A. 14 B. 16 C. 13 D. 11
10.如图,一根直的铁丝AB=20cm,欲将其弯折成一个三角形,在同一平面内操作如下:
①量出AP=5 cm;
②在点P右侧取一点Q,使点Q满足PQ>5cm;
③将AP 向右翻折,BQ向左翻折。
若要使A,B两点能在点M 处重合,则PQ的长度可能是 ( )
A. 12 cm B.11 cm C. 10 cm D. 7 cm
11.若△ABC的两边长是方程组 ,的解,第三边长为整数,则符合条件的三角形有__________个。
12.已知△ABC 的边 AB,边BC的长度分别是不等式组的最大整数解与最小整数解,如果△ABC的周长是奇数,则△ABC 的第三条边 AC 的长度的最小值为___________。
13.六边形钢架ABCDEF 由6条钢条铰接而成,如图所示,为使这一钢架稳固,试用三条钢条连接使之不能活动,方法很多,请至少画出三种方法。(只需画图,不必写出作法)
14.五一假期期间,小梦一家计划从家(点B)出发,到景点 C 游玩,如图所示。由于B,C之间是一条河,无法通过,只有BAC和 BPC两条路线,哪一条路线比较近?为什么?
15.已知a,b,c分别为△ABC 的三边长,且满足.
(1)求c的取值范围。
(2)若△ABC 的周长为21,求a,b,c 的值。
创新拓展题
16.综合与探究
【问题情境】小明和小红在一本数学资料书上看到有这样一道题目:“已知△ABC 的三边长分别为a,b,c(a>b),且满足( ,求c的取值范围。”
【思路分析】小明说:“把b+c看作一个整体,我能求出a的值。”
小红说:“我求不出c 的取值范围,但我能用含c的代数式表示b.”
小明和小红一起去请教李老师,李老师说:“根据你们二人的思路求解,再结合三角形的三边关系,即可得到c的取值范围。”
【问题解决】
(1)你知道小明是如何计算a的值的吗?请你写出求解的过程。
(2)请你用含 c的代数式表示b:_____________.
(3)请你根据李老师的提示,求c的取值范围。
参考答案
1. C 2. A 3. A 4.三角形具有稳定性
5.2b-2c 【点拨】∵△ABC的三边长分别是a,b,c,∴a+b>c,b-ac<0,
∴|a+b-c|-|b-a-c|=a+b-c-(-b+a+c)=a+b-c+b-a-c=2b-2c.
6.4
7.【解】(1)∵三角形的三边关系是:两边之和大于第三边,两边之差小于第三边,∴9-4<x<9+4,∴5<x<13.
(2)若△ABC为等腰三角形,则x=4或9,
当x=4时,不符合三角形的三边关系,应舍去,∴x=9,
∴等腰三角形ABC的周长=9+9+4=22.
8. C【点拨】由题意知,中间长方形的宽为(8-2a),则有,计算求解然后判断作答即可。
9. C【点拨】选AB+BC,CD,AD构造三角形,则三边长为14,7,6,14>7+6,不能构成三角形,此种情况不成立;选AB+AD,BC,CD构造三角形,则三边长为11,9,7,9-7<11<9+7,能构成三角形,此时两个顶点的距离最大值为11,选AB,BC+CD,AD构造三角形,则三边长为5,16,6,5+6<16, 不能构成三角形,此种情况不成立;选AB,BC,CD+AD构造三角形,则三边长为5,9,13,9-5<13<9+5,能构成三角形,此时两个顶点的距离最大值为13.综上,两个顶点的距离最大值为13.故选C.
10. D【点拨】设PQ=xcm(x>5).∵AP=5cm,PQ= xcm,∴BQ=AB-APPQ=20-5-x=(15-x) cm.∵将AP向右翻折,BQ向左翻折,∴AP=MP,MQ=BQ.∵△MPQ满足三角形三边关系,∴MQ-MP
x+5,即10-x
故选D.
11.3
12.3【点拨】解不等式组得,不等式组的最大整数解为8,最小整数解为6.∵△ABC的周长是奇数,8+6=14是偶数,且8-6<AC<8+6,∴△ABC的第三条边AC的长度的最小值为3.
13.【解】如图所示。(画法不唯一)
14.【解】路线BPC比较近。
理由:如图,延长BP交AC于点D,
∴路线BPC比较近。
15.【解】(1)根据三角形三边关系可知a+b>c,a-b∵a+b-4c+24=0,a-b-2c+10=0,∴a+b=4c-24,a-b=2c-10,
∴解得8<c<10.
(2)由(1)得 整理得
∵△ABC的周长为21,∴a+b+c=21,即3c-17+c-7+c=21,解得c=9,
∴a=3×9-17=10,b=9-7=2.
16.【解】(1)根据题意,得
(2)
(3)由三角形的三边关系,得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十三章 三角形
13.2 与三角形有关的线段
13.2.1 三角形的边
基础提优题目
1.满足下列条件的三条线段a,b,c,能组成三角形的有 ( )
A.①② B.③④ C.①④ D.①③
2.如图,人字梯的支架AB,AC的长度都为2m(连接处的长度忽略不计),则B,C两点之间的距离可能是 ( )
A. 3 m B. 4.2 m C. 5 m D. 6 m
3.若使用如图所示的①②两根铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以折成两段的铁丝是( )
A.只有①可以 B.只有②可以 C.①②都可以 D.①②都不可以
4.2024年10 月30日4时27分,搭载神舟十九号载人飞船的长征二号F遥十九运载火箭在酒泉卫星发射中心点火发射。在发射运载火箭时,运载火箭的发射架被焊接成了许多的三角形,这样做的原因是:_________________________________.
5.已知△ABC的三边长为a,b,c,化简的结果是_____________。
6.学具盒中装有四根长度分别为1 cm,3 cm,4 cm和5 cm 的细木棒,小明手中有一根长度为3cm的细木棒,现从盒中取出两根细木棒与小明手中的细木棒放在一起组成三角形,可以组成__________种不同的三角形。
7.已知△ABC的三边长分别为4,9,x.
(1)求x的取值范围;
(2)若它是一个等腰三角形,求它的周长。
综合应用题
8.如图①,将长为8 的长方形纸片沿虚线折成3个长方形,其中左、右两侧长方形的宽相等,若要将其围成如图②所示的三棱柱形物体,则图中a的范围是)
(第8题) (第9题)
9.如图,用AB,BC,CD,AD 四条钢条固定成一个框,相邻两钢条的夹角均可调整,不计螺丝大小及重叠部分。若AB=5,BC=9,CD=7,AD=6, 则所固定成的框中,两个顶点的距离最大值是 ( )
A. 14 B. 16 C. 13 D. 11
10.如图,一根直的铁丝AB=20cm,欲将其弯折成一个三角形,在同一平面内操作如下:
①量出AP=5 cm;
②在点P右侧取一点Q,使点Q满足PQ>5cm;
③将AP 向右翻折,BQ向左翻折。
若要使A,B两点能在点M 处重合,则PQ的长度可能是 ( )
A. 12 cm B.11 cm C. 10 cm D. 7 cm
11.若△ABC的两边长是方程组 ,的解,第三边长为整数,则符合条件的三角形有__________个。
12.已知△ABC 的边 AB,边BC的长度分别是不等式组的最大整数解与最小整数解,如果△ABC的周长是奇数,则△ABC 的第三条边 AC 的长度的最小值为___________。
13.六边形钢架ABCDEF 由6条钢条铰接而成,如图所示,为使这一钢架稳固,试用三条钢条连接使之不能活动,方法很多,请至少画出三种方法。(只需画图,不必写出作法)
14.五一假期期间,小梦一家计划从家(点B)出发,到景点 C 游玩,如图所示。由于B,C之间是一条河,无法通过,只有BAC和 BPC两条路线,哪一条路线比较近?为什么?
15.已知a,b,c分别为△ABC 的三边长,且满足.
(1)求c的取值范围。
(2)若△ABC 的周长为21,求a,b,c 的值。
创新拓展题
16.综合与探究
【问题情境】小明和小红在一本数学资料书上看到有这样一道题目:“已知△ABC 的三边长分别为a,b,c(a>b),且满足( ,求c的取值范围。”
【思路分析】小明说:“把b+c看作一个整体,我能求出a的值。”
小红说:“我求不出c 的取值范围,但我能用含c的代数式表示b.”
小明和小红一起去请教李老师,李老师说:“根据你们二人的思路求解,再结合三角形的三边关系,即可得到c的取值范围。”
【问题解决】
(1)你知道小明是如何计算a的值的吗?请你写出求解的过程。
(2)请你用含 c的代数式表示b:_____________.
(3)请你根据李老师的提示,求c的取值范围。
参考答案
1. C 2. A 3. A 4.三角形具有稳定性
5.2b-2c 【点拨】∵△ABC的三边长分别是a,b,c,∴a+b>c,b-ac<0,
∴|a+b-c|-|b-a-c|=a+b-c-(-b+a+c)=a+b-c+b-a-c=2b-2c.
6.4
7.【解】(1)∵三角形的三边关系是:两边之和大于第三边,两边之差小于第三边,∴9-4<x<9+4,∴5<x<13.
(2)若△ABC为等腰三角形,则x=4或9,
当x=4时,不符合三角形的三边关系,应舍去,∴x=9,
∴等腰三角形ABC的周长=9+9+4=22.
8. C【点拨】由题意知,中间长方形的宽为(8-2a),则有,计算求解然后判断作答即可。
9. C【点拨】选AB+BC,CD,AD构造三角形,则三边长为14,7,6,14>7+6,不能构成三角形,此种情况不成立;选AB+AD,BC,CD构造三角形,则三边长为11,9,7,9-7<11<9+7,能构成三角形,此时两个顶点的距离最大值为11,选AB,BC+CD,AD构造三角形,则三边长为5,16,6,5+6<16, 不能构成三角形,此种情况不成立;选AB,BC,CD+AD构造三角形,则三边长为5,9,13,9-5<13<9+5,能构成三角形,此时两个顶点的距离最大值为13.综上,两个顶点的距离最大值为13.故选C.
10. D【点拨】设PQ=xcm(x>5).∵AP=5cm,PQ= xcm,∴BQ=AB-APPQ=20-5-x=(15-x) cm.∵将AP向右翻折,BQ向左翻折,∴AP=MP,MQ=BQ.∵△MPQ满足三角形三边关系,∴MQ-MP
x+5,即10-x
故选D.
11.3
12.3【点拨】解不等式组得,不等式组的最大整数解为8,最小整数解为6.∵△ABC的周长是奇数,8+6=14是偶数,且8-6<AC<8+6,∴△ABC的第三条边AC的长度的最小值为3.
13.【解】如图所示。(画法不唯一)
14.【解】路线BPC比较近。
理由:如图,延长BP交AC于点D,
∴路线BPC比较近。
15.【解】(1)根据三角形三边关系可知a+b>c,a-b
∴解得8<c<10.
(2)由(1)得 整理得
∵△ABC的周长为21,∴a+b+c=21,即3c-17+c-7+c=21,解得c=9,
∴a=3×9-17=10,b=9-7=2.
16.【解】(1)根据题意,得
(2)
(3)由三角形的三边关系,得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
