13.3.1.1 三角形的内角 同步练习(含答案)
文档属性
| 名称 | 13.3.1.1 三角形的内角 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 759.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十三章 三角形
13.3三角形的内角与外角
13.3.1 三角形的内角
第1课时 三角形的内角和
基础提优题
1.如图,在△ABC中,∠B=46°,∠C=54°,AD 平分∠BAC,交 BC 于点 D,则∠BAD 的大小是 ( )
A. 45° B. 54° C. 40° D. 50°
(第1题) (第2题)
2.如图,点 E,D分别在AB,AC上,若∠B=30°,∠C=55°,则∠1+∠2的度数为( )
A. 85° B. 80° C. 75° D. 70°
3. 在△ABC 中,∠A:∠B:∠C=1:2:3,则△ABC ( )
A.是锐角三角形 B.是直角三角形 C.是钝角三角形 D.不存在
4.如图,∠A=70°,BP,CP 分别平分∠ABC和∠ACB,则∠P 的度数是( )
A. 125° B. 115° C. 110° D. 120°
(第4题) (第5题)
5.如图,考古学家发现在地下A处有一座古墓,古墓上方是燃气管道,为了不影响管道,准备B处和C处开工挖出“V”字形通道。若∠DBA=120°,∠ECA=135°,则∠A的度数是_____________.
6.如图,点 C 在点 B 的北偏西60°方向上,点 C 在点 A 的北偏西30°方向上,点 B 在点 A的北偏东30°方向上。
(1)求∠ABC的大小;
(2)求∠C的大小。
综合应用题
7.新疆维吾斯学校级期中如图,两面镜子AB,BC的夹角为∠α,当光线经过镜子反射后,∠1=∠2, ∠3=∠4.若∠α=68°,则∠β的度数是( )
A. 44° B. 45° C. 46° D. 47°
(第7题) (第8题)
8.如图,在△ABC中,点 D 在BC上,点 E,F 在AB 上,点 G在DF 的延长线上,且∠B=∠DFB,∠G=∠DEG,若∠BEG=29°,则∠BDE 的度数为 ( )
A. 61° B. 58° C. 65.5° D. 59.5°
9.如图,在△ABC中,∠A=40°,∠B=68°,E是△ABC的角平分线CF 延长线上一动点(不与点 F 重合),过点 E 作 ED⊥AB于点 D,当点 E运动时,∠E的度数( )
A.随点 E 的运动而变化,离点 F 越近,度数越大
B.不变,为16°
C.随点 E 的运动而变化,离点F 越远,度数越大
D.不变,为14°
10.七巧板是我国一款传统的益智玩具,由宋朝的“宴几”演变而来,能够启迪智慧,陶冶情操。七巧板是由五块含45°角的直角三角形、一块正方形和一块平行四边形组成的。某同学利用图①(外轮廓为正方形)中的部分图形拼成图②。若 ∠1=∠2=45°,则∠3的度数为_____________°。
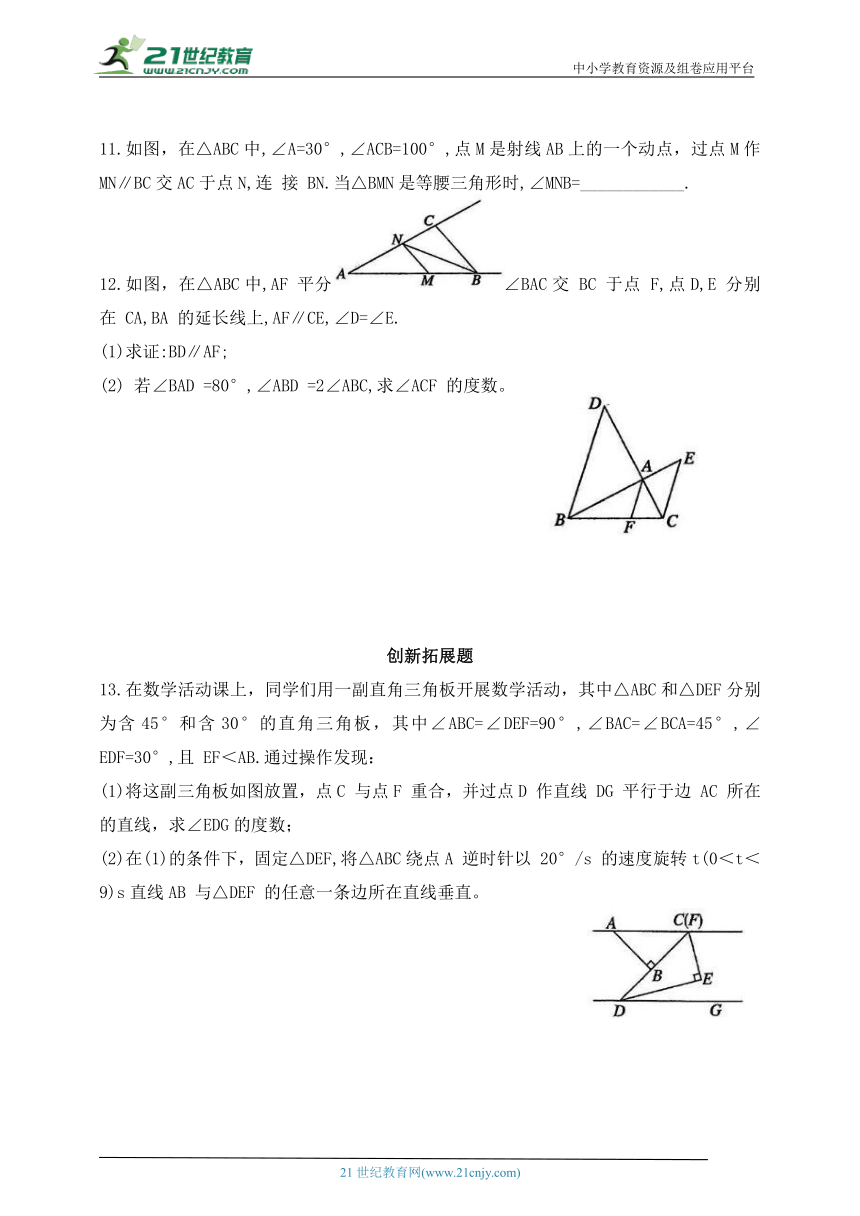
11.如图,在△ABC中,∠A=30°,∠ACB=100°,点M是射线AB上的一个动点,过点M作MN∥BC交AC于点N,连 接 BN.当△BMN是等腰三角形时,∠MNB=____________.
12.如图,在△ABC中,AF 平分∠BAC交 BC 于点 F,点D,E 分别在 CA,BA 的延长线上,AF∥CE,∠D=∠E.
(1)求证:BD∥AF;
(2) 若∠BAD =80°,∠ABD =2∠ABC,求∠ACF 的度数。
创新拓展题
13.在数学活动课上,同学们用一副直角三角板开展数学活动,其中△ABC和△DEF分别为含45°和含30°的直角三角板,其中∠ABC=∠DEF=90°,∠BAC=∠BCA=45°,∠EDF=30°,且 EF<AB.通过操作发现:
(1)将这副三角板如图放置,点C 与点F 重合,并过点D 作直线 DG 平行于边 AC 所在的直线,求∠EDG的度数;
(2)在(1)的条件下,固定△DEF,将△ABC绕点A 逆时针以 20°/s 的速度旋转t(0<t<9)s直线AB 与△DEF 的任意一条边所在直线垂直。
参考答案
1. C 2. A 3. B
4. A 【点拨】∵BP,CP分别平分∠ABC和∠ACB,
在△PBC中,∠P +∠PBC+∠PCB =180°,∴∠PBC=∠ABC,∠PCB=∠ACB.
在△PBC中,∠P+∠PBC+∠PCB=180°,∴∠P=180°-
=180°-(180°-∠A)=90°+ ∠A.
∵∠A=70°,∴∠P=125°.
点规律 两内角平分线的夹角公式:如图,在△ABC中,BO,CO分别平分∠ABC和 ∠ACB,则
5.75°【点拨】∵∠DBA=120°,∠ECA=135°,∴∠ABC=60°,∠ACB=45°,
∴∠A=180°-∠ABC-∠ACB=75°.
6.【解】(1)如图,根据题意可得 ∠1=60°∠3=30°.
∵AE∥DB,∴∠2=∠3=30°,∴∠ABC=180°-60°-30°=90°.
(2)∵∠3=30°,∠4=30°,∠ABC=90°,∴∠C=180°-90°-30°-30°=30°.
7. A【点拨】如图,
∵∠α=68°,∴∠2+∠3=180°-
2,∠3=∠4,∴∠1+∠2+∠3+∠4=2,
,
8. B
9. D【点拨】∵∠A=40°,∠B=68°,∴∠BCA=180°-40°-68°=72°.
∵CF平分∠BCA,∴∠BCF=∠BCA=36°,∴∠BFC=180°-36°-68°=76°,∴∠EFD=76°.∵ED⊥AB,∴∠FED=180°-90°-76°=14°,∴当点E运动时,∠E的度数不变,为14°.
10.90 【点拨】如图,由题意得,∠EAB=45°,∠CBD=90°,∠ACF=90°-45°=45°.∵∠1=∠2=45°,
∴∠ABC=180°-∠1-∠D=45°,∠BAC=180°-∠BAE-∠2=90°,∴∠ACB=180°-∠BAC- ,
.
11.25°或50°或65°或80°
【点拨】∵∠A=30°,∠ACB=100°,∴∠ABC=180°-100°-30°=50°.
∵MN∥BC,∴∠AMN=∠ABC=50°.
当点M在线段AB上时,MN= MB,∴∠MNB = ∠MBN,易得∠AMN =, ;
当点M在AB延长线上时,①若 MN=MB,∴∠MNB= ②若BN=MB,∴∠MNB=∠BMN=50°;③若BN=MN,∴易得∠MNB=180°-2∠AMN=80°.综上,∠MNB=25°或50°或65°或80°.
12.(1)【证明】∵AF平分∠BAC,∴∠BAF=∠CAF.
∵AF∥CE,∴∠E=∠BAF,∴∠E=∠CAF.
又∵∠D=∠E,∴∠D=∠CAF,∴BD∥AF.
(2)【解】由(1)知BD∥AF,∴∠ABF=∠BAF.
∵AF平分∠BAC,∴∠BAC=2∠BAF=2∠ABD.
∵ ∠ABD =2∠ABC,∴∠BAC=4∠ABC.
∵∠BAD=80°,∴∠BAC=180°-∠BAD=100°,,
13.【解】(1)∵AC∥DG,∴∠CDG=∠ACB=45°,∴∠ED G=∠CDG-∠CDE=45°-30°=15°.
(2)∵∠AFD=45°,∠DFE=60°,∴∠AFE=∠AFD+∠DFE=45°+60°=105°.
当AB⊥EF时,如图①,设直线AB,EF C交于点H,过点H作HK∥AF.
∵HK∥AF,∴∠KHF=∠AFE=105°,∠FAH=∠KHA,
∴∠KHA = ∠FAH = ∠KHF-∠AHE=105°-90°=15°.
∵∠HAC=45°,∴∠CAF=∠HAC+∠FAH=45°+15°=60°,
∴20t=60,解得t=3;
当AB⊥DE时,如图②,设直线AB,DE交于点M,则∠AME=90°,
∴∠AME+∠E=90°+90°=180°,∴AB∥EF,
∴∠BAF=∠AFE=105°,∴∠CAF=∠BAC+∠BAF=45°,
∴20t=150,解得t=7.5;
当AB⊥DF时,如图③,设直线AB,DF交于点N,则∠BNF =90°,
∴∠B=∠BNF=90°,∴BC∥DF.∴∠CAF=180°.
∴20t=180,解得t=9.
综上所述,当a=3或7.5或9时,直线AB与△DEF的任意一条边所在直线垂直。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十三章 三角形
13.3三角形的内角与外角
13.3.1 三角形的内角
第1课时 三角形的内角和
基础提优题
1.如图,在△ABC中,∠B=46°,∠C=54°,AD 平分∠BAC,交 BC 于点 D,则∠BAD 的大小是 ( )
A. 45° B. 54° C. 40° D. 50°
(第1题) (第2题)
2.如图,点 E,D分别在AB,AC上,若∠B=30°,∠C=55°,则∠1+∠2的度数为( )
A. 85° B. 80° C. 75° D. 70°
3. 在△ABC 中,∠A:∠B:∠C=1:2:3,则△ABC ( )
A.是锐角三角形 B.是直角三角形 C.是钝角三角形 D.不存在
4.如图,∠A=70°,BP,CP 分别平分∠ABC和∠ACB,则∠P 的度数是( )
A. 125° B. 115° C. 110° D. 120°
(第4题) (第5题)
5.如图,考古学家发现在地下A处有一座古墓,古墓上方是燃气管道,为了不影响管道,准备B处和C处开工挖出“V”字形通道。若∠DBA=120°,∠ECA=135°,则∠A的度数是_____________.
6.如图,点 C 在点 B 的北偏西60°方向上,点 C 在点 A 的北偏西30°方向上,点 B 在点 A的北偏东30°方向上。
(1)求∠ABC的大小;
(2)求∠C的大小。
综合应用题
7.新疆维吾斯学校级期中如图,两面镜子AB,BC的夹角为∠α,当光线经过镜子反射后,∠1=∠2, ∠3=∠4.若∠α=68°,则∠β的度数是( )
A. 44° B. 45° C. 46° D. 47°
(第7题) (第8题)
8.如图,在△ABC中,点 D 在BC上,点 E,F 在AB 上,点 G在DF 的延长线上,且∠B=∠DFB,∠G=∠DEG,若∠BEG=29°,则∠BDE 的度数为 ( )
A. 61° B. 58° C. 65.5° D. 59.5°
9.如图,在△ABC中,∠A=40°,∠B=68°,E是△ABC的角平分线CF 延长线上一动点(不与点 F 重合),过点 E 作 ED⊥AB于点 D,当点 E运动时,∠E的度数( )
A.随点 E 的运动而变化,离点 F 越近,度数越大
B.不变,为16°
C.随点 E 的运动而变化,离点F 越远,度数越大
D.不变,为14°
10.七巧板是我国一款传统的益智玩具,由宋朝的“宴几”演变而来,能够启迪智慧,陶冶情操。七巧板是由五块含45°角的直角三角形、一块正方形和一块平行四边形组成的。某同学利用图①(外轮廓为正方形)中的部分图形拼成图②。若 ∠1=∠2=45°,则∠3的度数为_____________°。
11.如图,在△ABC中,∠A=30°,∠ACB=100°,点M是射线AB上的一个动点,过点M作MN∥BC交AC于点N,连 接 BN.当△BMN是等腰三角形时,∠MNB=____________.
12.如图,在△ABC中,AF 平分∠BAC交 BC 于点 F,点D,E 分别在 CA,BA 的延长线上,AF∥CE,∠D=∠E.
(1)求证:BD∥AF;
(2) 若∠BAD =80°,∠ABD =2∠ABC,求∠ACF 的度数。
创新拓展题
13.在数学活动课上,同学们用一副直角三角板开展数学活动,其中△ABC和△DEF分别为含45°和含30°的直角三角板,其中∠ABC=∠DEF=90°,∠BAC=∠BCA=45°,∠EDF=30°,且 EF<AB.通过操作发现:
(1)将这副三角板如图放置,点C 与点F 重合,并过点D 作直线 DG 平行于边 AC 所在的直线,求∠EDG的度数;
(2)在(1)的条件下,固定△DEF,将△ABC绕点A 逆时针以 20°/s 的速度旋转t(0<t<9)s直线AB 与△DEF 的任意一条边所在直线垂直。
参考答案
1. C 2. A 3. B
4. A 【点拨】∵BP,CP分别平分∠ABC和∠ACB,
在△PBC中,∠P +∠PBC+∠PCB =180°,∴∠PBC=∠ABC,∠PCB=∠ACB.
在△PBC中,∠P+∠PBC+∠PCB=180°,∴∠P=180°-
=180°-(180°-∠A)=90°+ ∠A.
∵∠A=70°,∴∠P=125°.
点规律 两内角平分线的夹角公式:如图,在△ABC中,BO,CO分别平分∠ABC和 ∠ACB,则
5.75°【点拨】∵∠DBA=120°,∠ECA=135°,∴∠ABC=60°,∠ACB=45°,
∴∠A=180°-∠ABC-∠ACB=75°.
6.【解】(1)如图,根据题意可得 ∠1=60°∠3=30°.
∵AE∥DB,∴∠2=∠3=30°,∴∠ABC=180°-60°-30°=90°.
(2)∵∠3=30°,∠4=30°,∠ABC=90°,∴∠C=180°-90°-30°-30°=30°.
7. A【点拨】如图,
∵∠α=68°,∴∠2+∠3=180°-
2,∠3=∠4,∴∠1+∠2+∠3+∠4=2,
,
8. B
9. D【点拨】∵∠A=40°,∠B=68°,∴∠BCA=180°-40°-68°=72°.
∵CF平分∠BCA,∴∠BCF=∠BCA=36°,∴∠BFC=180°-36°-68°=76°,∴∠EFD=76°.∵ED⊥AB,∴∠FED=180°-90°-76°=14°,∴当点E运动时,∠E的度数不变,为14°.
10.90 【点拨】如图,由题意得,∠EAB=45°,∠CBD=90°,∠ACF=90°-45°=45°.∵∠1=∠2=45°,
∴∠ABC=180°-∠1-∠D=45°,∠BAC=180°-∠BAE-∠2=90°,∴∠ACB=180°-∠BAC- ,
.
11.25°或50°或65°或80°
【点拨】∵∠A=30°,∠ACB=100°,∴∠ABC=180°-100°-30°=50°.
∵MN∥BC,∴∠AMN=∠ABC=50°.
当点M在线段AB上时,MN= MB,∴∠MNB = ∠MBN,易得∠AMN =, ;
当点M在AB延长线上时,①若 MN=MB,∴∠MNB= ②若BN=MB,∴∠MNB=∠BMN=50°;③若BN=MN,∴易得∠MNB=180°-2∠AMN=80°.综上,∠MNB=25°或50°或65°或80°.
12.(1)【证明】∵AF平分∠BAC,∴∠BAF=∠CAF.
∵AF∥CE,∴∠E=∠BAF,∴∠E=∠CAF.
又∵∠D=∠E,∴∠D=∠CAF,∴BD∥AF.
(2)【解】由(1)知BD∥AF,∴∠ABF=∠BAF.
∵AF平分∠BAC,∴∠BAC=2∠BAF=2∠ABD.
∵ ∠ABD =2∠ABC,∴∠BAC=4∠ABC.
∵∠BAD=80°,∴∠BAC=180°-∠BAD=100°,,
13.【解】(1)∵AC∥DG,∴∠CDG=∠ACB=45°,∴∠ED G=∠CDG-∠CDE=45°-30°=15°.
(2)∵∠AFD=45°,∠DFE=60°,∴∠AFE=∠AFD+∠DFE=45°+60°=105°.
当AB⊥EF时,如图①,设直线AB,EF C交于点H,过点H作HK∥AF.
∵HK∥AF,∴∠KHF=∠AFE=105°,∠FAH=∠KHA,
∴∠KHA = ∠FAH = ∠KHF-∠AHE=105°-90°=15°.
∵∠HAC=45°,∴∠CAF=∠HAC+∠FAH=45°+15°=60°,
∴20t=60,解得t=3;
当AB⊥DE时,如图②,设直线AB,DE交于点M,则∠AME=90°,
∴∠AME+∠E=90°+90°=180°,∴AB∥EF,
∴∠BAF=∠AFE=105°,∴∠CAF=∠BAC+∠BAF=45°,
∴20t=150,解得t=7.5;
当AB⊥DF时,如图③,设直线AB,DF交于点N,则∠BNF =90°,
∴∠B=∠BNF=90°,∴BC∥DF.∴∠CAF=180°.
∴20t=180,解得t=9.
综上所述,当a=3或7.5或9时,直线AB与△DEF的任意一条边所在直线垂直。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
