广东省广州市天河区2024-2025学年七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 广东省广州市天河区2024-2025学年七年级(下)期末数学试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 00:00:00 | ||
图片预览




文档简介
2024-2025学年广东省广州市天河区七年级(下)期末数学试卷
一、单项选择题(本题有10个小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的.)
1.(3分)下列各数中,属于无理数的是( )
A. B.﹣3 C.3.1415926 D.
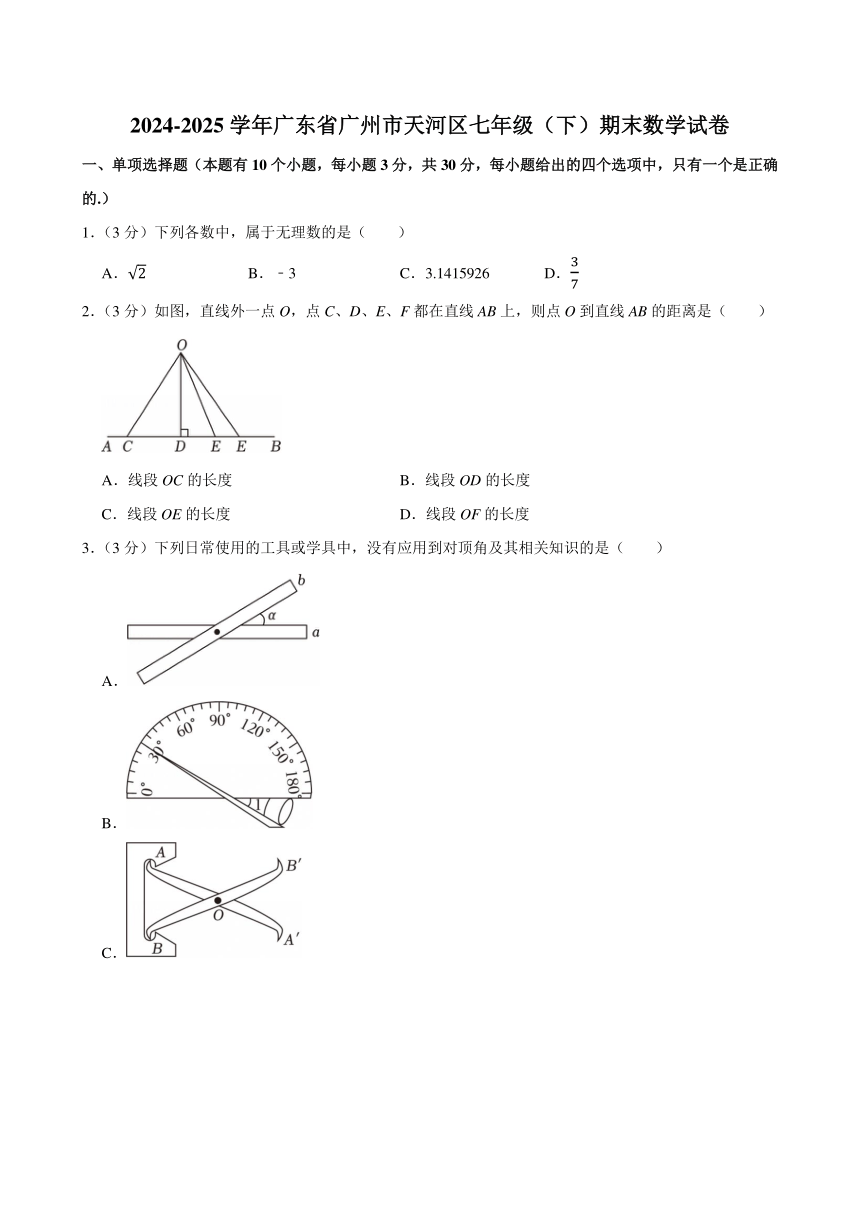
2.(3分)如图,直线外一点O,点C、D、E、F都在直线AB上,则点O到直线AB的距离是( )
A.线段OC的长度 B.线段OD的长度
C.线段OE的长度 D.线段OF的长度
3.(3分)下列日常使用的工具或学具中,没有应用到对顶角及其相关知识的是( )
A.
B.
C.
D.
4.(3分)在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(3分)若m>n,则下列各式中正确的是( )
A.m+2<n+2 B.m﹣3<n﹣3 C.﹣5m<﹣5n D.
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
7.(3分)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOA=135°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
8.(3分)下列命题中,真命题是( )
A.相等的角是对顶角
B.在同一平面内,垂直于同一条直线的两条直线平行
C.两条直线被第三条直线所截,同位角相等
D.同旁内角互补
9.(3分)如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图案,已知B(2,4),则点A的坐标为( )
A.(4,5) B.(5,5) C.(5,6) D.(6,6)
10.(3分)已知关于x,y的二元一次方程ax+b=y,当x分别取值时对于y的值如表所示,则关于x的不等式ax+b<0的解集为( )
x … ﹣1 0 1 2 3 …
y … 3 2 1 0 ﹣1 …
A.x<0 B.x>0 C.x<2 D.x>2
二、填空题(本题有5个小题,每小题3分,共15分。)
11.(3分)﹣64的立方根是 .
12.(3分)用适当的符号表示不等关系“m与3的和小于5”,则可以得到数学表达式为 .
13.(3分)为了研究气温对冷饮销售的影响,一家饮品店经过一段时间的统计,得到一组卖出的冷饮杯数与当天最高气温的数据,用如图所示的趋势图描述这家饮品店一天中卖出的冷饮杯数与当天的最高气温之间的关系.根据所作的趋势图,估计当一天的最高气温为30℃时,饮品店卖出的冷饮杯数约为 .
14.(3分)仰卧起坐是增加躯干肌肉力量和伸张性的一种运动,能够很好的锻炼腹部肌肉,如图是小美同学做仰卧起坐运动某一瞬间的动作及其示意图,AB∥CD,AC∥DE,点F在直线AC上,∠FAB=120°,∠E=55°,则∠DCE的度数为 .
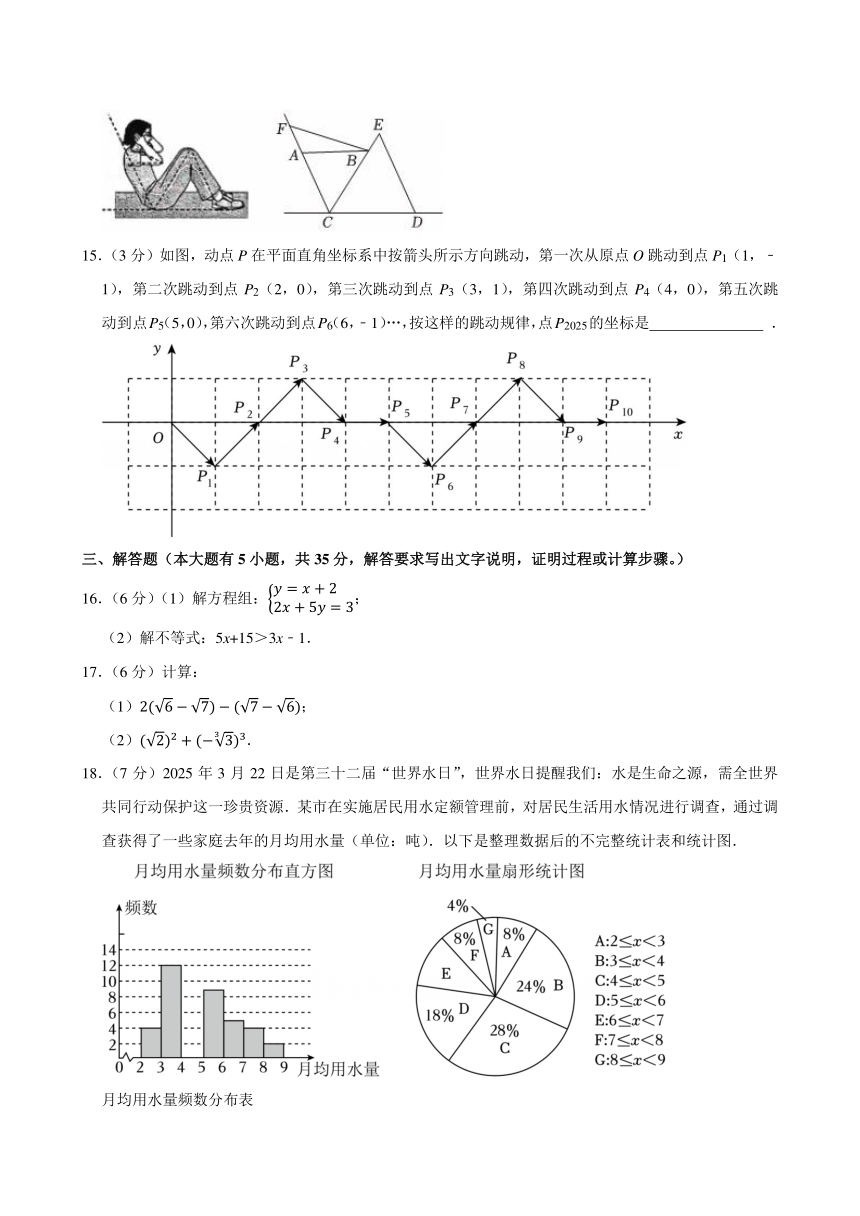
15.(3分)如图,动点P在平面直角坐标系中按箭头所示方向跳动,第一次从原点O跳动到点P1(1,﹣1),第二次跳动到点P2(2,0),第三次跳动到点P3(3,1),第四次跳动到点P4(4,0),第五次跳动到点P5(5,0),第六次跳动到点P6(6,﹣1)…,按这样的跳动规律,点P2025的坐标是 .
三、解答题(本大题有5小题,共35分,解答要求写出文字说明,证明过程或计算步骤。)
16.(6分)(1)解方程组:;
(2)解不等式:5x+15>3x﹣1.
17.(6分)计算:
(1);
(2).
18.(7分)2025年3月22日是第三十二届“世界水日”,世界水日提醒我们:水是生命之源,需全世界共同行动保护这一珍贵资源.某市在实施居民用水定额管理前,对居民生活用水情况进行调查,通过调查获得了一些家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整统计表和统计图.
月均用水量频数分布表
分组 频数
2≤x<3 4
3≤x<4 12
4≤x<5 a
5≤x<6 9
6≤x<7 5
7≤x<8 4
8≤x<9 2
请根据不完整的图表中提供的信息解答下列问题:
(1)填空:
①本次调查的样本容量是 ;
②频数分布表中a的值为 ;
③月均用水量扇形统计图中,分组“E”的扇形圆心角度数是 ;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?请说明理由.
19.(8分)如图,∠ABC的边BC和∠DEF的边FE相交于点G,且AB∥FE.
(1)若DE∥BC,∠B=60°,求∠DEF的度数;
(2)按照要求完成以下证明,括号内填写推理的依据.
若∠B+∠DEF=180°,求证:BC∥DE.
证明:∵AB∥FE,
∴ ( ).
∵∠B+∠E=180°,
∴ .
∴BC∥DE( ).
20.(8分)天气晴朗时,一个人能看到大海的最远距离s(单位:千米)可用公式来估计,其中h(单位:米)是眼睛离海平面的高度.
(1)如果小天站在岸边观察,当眼睛离海平面的高度是1.6米时,能看到多远?
(2)若小天登上岸边的一个观望台A,已知小天眼睛离观望台地面的高度是1.6米,他想看到距离岸边大约10千米处的一个货轮B,则观望台至少离海平面高多少米才可以看得见?
四、解答题(本大题有3小题,共40分,解答要求写出文字说明,证明过程或计算步骤。)
21.(16分)如图是由小正方形组成的网格,△ABC的三个顶点都在小正方形的顶点上,在网格上建立平面直角坐标系.已知A(﹣1,4),B(﹣4,0),C(﹣2,﹣2).
(1)取一点D(3,3),将三角形ABC平移至三角形DEF,其中点A的对应点为D,画出三角形DEF,并求其面积;
(2)在x轴上取一点G(x,0),其中x为整数,且满足x≥﹣4,若使三角形ABG的面积小于10,求点G的坐标;
(3)本小题为多项选择题,有多个选项符合题目要求,要求回答时,全部选对的得满分,选对但不全的视正确答案数相应给分,有选错的得0分.题目如下:
若将三角形ABC向左或向右平移,得到点A的三个对应点M(m,4),点P(2m﹣1,4),点N(n,4),则下列说法正确的是 .
A.当m<1时,点M始终在点P的左边
B.当m>1时,点M始终在点P的左边
C.当m<1且n=﹣2时,存在m的值,使得点N在线段MP上
D.当m>1且n=2时,存在m的值,使得点N在线段MP上
22.(12分)【阅读理解】在小学,我们知道三角形的三个内角和等于180°,也即是,如图1,三角形ABC中,∠A+∠B+∠C=180°,学习平行线后,只需过点A作BC的平行线DE,就把三角形的三个角“聚合”在一起形成一个平角(∠A+∠B+∠C=∠BAC+∠1+∠2=180°).
【解决问题】应用类似的方法,在图2的四边形ABCD中添加适当的平行线,运用平行线的性质以及平角、周角和对顶角等相关知识求出四边形ABCD的四个内角和(即∠A+∠B+∠C+∠D)的度数,并说明理由(注意:不能直接用三角形的三个内角和等于180°的结论).
23.(12分)本学期,教科书在七年级下册第十一章《二元一次方程组》的“阅读与思考”栏目中,介绍了《中国古代著名的一次不定方程组问题》,其中有《张丘建算经》记载的“百鸡问题”,意思是:如果一只公鸡值5个钱,一只母鸡值3个钱,3只小鸡值1个钱,现用100个钱,买了100只鸡,问公鸡、母鸡、小鸡各买了多少只?
小天和小河对此很感兴趣,一起展开了研究,提出以下两个问题.
(1)小天提出的问题是:若公鸡买了8只,则母鸡、小鸡各买了多少只?
(2)小河解答了小天的问题后,找到了一个求解“百鸡问题”的方法:设公鸡、母鸡、小鸡各买了x只,y只,z只,依题意得到方程组,把②×3﹣①,消去z,得到一个二元一次方程7x+4y=100.小河说:“由于是这个二元一次方程的一组解,因此该方程的解可以含字母t的式子表示,即为(t为整数),根据题意,由x,y的取值范围可以求出t的值,由此可求出满足条件的公鸡、母鸡、小鸡的数量情况.
现在,请你先解答小天的问题,然后把小河求解“百鸡问题”的过程补充完整.
2024-2025学年广东省广州市天河区七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D B C D C B B D
一、单项选择题(本题有10个小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的.)
1.(3分)下列各数中,属于无理数的是( )
A. B.﹣3 C.3.1415926 D.
【解答】解:A、是无理数,故此选项符合题意;
B、﹣3是有理数,故此选项不符合题意;
C、3.1415926是有理数,故此选项不符合题意;
D、是有理数,故此选项不符合题意;
故选:A.
2.(3分)如图,直线外一点O,点C、D、E、F都在直线AB上,则点O到直线AB的距离是( )
A.线段OC的长度 B.线段OD的长度
C.线段OE的长度 D.线段OF的长度
【解答】解:∵直线外一点到直线的垂线段的长度,叫做点到直线的距离,
∴由图可知,点O到直线AB的距离是线段OD的长度.
故选:B.
3.(3分)下列日常使用的工具或学具中,没有应用到对顶角及其相关知识的是( )
A.
B.
C.
D.
【解答】解:选项A,选项B,选项C中的工具,利用了对顶角相等,而选项D利用的是“画一条线段等于已知线段”,
故选:D.
4.(3分)在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:点(﹣5,2)在第二象限.
故选:B.
5.(3分)若m>n,则下列各式中正确的是( )
A.m+2<n+2 B.m﹣3<n﹣3 C.﹣5m<﹣5n D.
【解答】解:A、在不等式m>n的两边同时加上2,不等号方向不变,即m+2>n+2,故本选项不符合题意.
B、在不等式m>n的两边同时减去3,不等号方向不变,即m﹣3>n﹣3,故本选项不符合题意.
C、在不等式m>n的两边同时乘﹣5,不等号方向改变,即﹣5m<﹣5n,故本选项符合题意.
D、在不等式m>n的两边同时除以6,不等号方向不变,即,故本选项不符合题意.
故选:C.
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
【解答】解:解不等式组得:,
∴不等式组的解集为:﹣1<x≤2,
在数轴上表示如图:
.
故选:D.
7.(3分)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOA=135°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
【解答】解:∵∠DOA=135°,
∴∠DOA=∠BOC=135°,
∵OE⊥AB,
∴∠BOE=90°,
∴∠COE=∠BOC﹣∠BOE=45°,
故选:C.
8.(3分)下列命题中,真命题是( )
A.相等的角是对顶角
B.在同一平面内,垂直于同一条直线的两条直线平行
C.两条直线被第三条直线所截,同位角相等
D.同旁内角互补
【解答】解:A、相等的角不一定是对顶角,故错误,是假命题,不符合题意;
B、在同一平面内,垂直于同一直线的两条直线平行,正确,是真命题,符合题意;
C、两条平行直线被第三条直线所截,同位角相等,故错误,是假命题,不符合题意;
D、两直线平行,同旁内角互补,故错误,是假命题,不符合题意.
故选:B.
9.(3分)如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图案,已知B(2,4),则点A的坐标为( )
A.(4,5) B.(5,5) C.(5,6) D.(6,6)
【解答】解:设长方形纸片的长为a,宽为b,
由B点坐标可以得到:
,
解得:,
∴点A的横坐标为:2×1+3=5,纵坐标为2×1+3=5,
故选:B.
10.(3分)已知关于x,y的二元一次方程ax+b=y,当x分别取值时对于y的值如表所示,则关于x的不等式ax+b<0的解集为( )
x … ﹣1 0 1 2 3 …
y … 3 2 1 0 ﹣1 …
A.x<0 B.x>0 C.x<2 D.x>2
【解答】解:由题意得出,
解得,
则不等式为﹣x+2<0,
解得x>2,
故选:D.
二、填空题(本题有5个小题,每小题3分,共15分。)
11.(3分)﹣64的立方根是 ﹣4 .
【解答】解:∵(﹣4)3=﹣64,
∴﹣64的立方根是﹣4.
故答案为:﹣4.
12.(3分)用适当的符号表示不等关系“m与3的和小于5”,则可以得到数学表达式为 m+3<5 .
【解答】解:由题意得:m+3<5,
故答案为:m+3<5.
13.(3分)为了研究气温对冷饮销售的影响,一家饮品店经过一段时间的统计,得到一组卖出的冷饮杯数与当天最高气温的数据,用如图所示的趋势图描述这家饮品店一天中卖出的冷饮杯数与当天的最高气温之间的关系.根据所作的趋势图,估计当一天的最高气温为30℃时,饮品店卖出的冷饮杯数约为 180 .
【解答】解:趋势图如图所示:
估计当一天的最高气温为30℃时,饮品店卖出的冷饮杯数约为180杯.
故答案为:180.
14.(3分)仰卧起坐是增加躯干肌肉力量和伸张性的一种运动,能够很好的锻炼腹部肌肉,如图是小美同学做仰卧起坐运动某一瞬间的动作及其示意图,AB∥CD,AC∥DE,点F在直线AC上,∠FAB=120°,∠E=55°,则∠DCE的度数为 65° .
【解答】解:∵AB∥CD,
∴∠ACD=∠FAB=120°,
∵AC∥DE,
∴∠ACE=∠E=55°,
∴∠DCE=120°﹣55°=65°.
故答案为:65°.
15.(3分)如图,动点P在平面直角坐标系中按箭头所示方向跳动,第一次从原点O跳动到点P1(1,﹣1),第二次跳动到点P2(2,0),第三次跳动到点P3(3,1),第四次跳动到点P4(4,0),第五次跳动到点P5(5,0),第六次跳动到点P6(6,﹣1)…,按这样的跳动规律,点P2025的坐标是 (2025,0) .
【解答】解:第一次从原点O跳动到点P1(1,﹣1),
第二次跳动到点P2(2,0),
第三次跳动到点P3(3,1),
第四次跳动到点P4(4,0),
第五次跳动到点P5(5,0),
第六次跳动到点P6(6,﹣1),
∴横坐标与所跳次数相同,即跳了n次,该点的横坐标为n,纵坐标每5次一循环,
∴2025÷5=405,
∴P2025(2025,0),
故答案为:(2025,0).
三、解答题(本大题有5小题,共35分,解答要求写出文字说明,证明过程或计算步骤。)
16.(6分)(1)解方程组:;
(2)解不等式:5x+15>3x﹣1.
【解答】解:(1),
①代入②,得:2x+5x+10=3,
解得x=﹣1,
将x=﹣1代入①得:y=1,
所以;
(2)∵5x+15>3x﹣1,
∴5x﹣3x>﹣1﹣15,
2x>﹣16,
则x>﹣8.
17.(6分)计算:
(1);
(2).
【解答】解:(1)
;
(2)
=2+(﹣3)
=﹣1.
18.(7分)2025年3月22日是第三十二届“世界水日”,世界水日提醒我们:水是生命之源,需全世界共同行动保护这一珍贵资源.某市在实施居民用水定额管理前,对居民生活用水情况进行调查,通过调查获得了一些家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整统计表和统计图.
月均用水量频数分布表
分组 频数
2≤x<3 4
3≤x<4 12
4≤x<5 a
5≤x<6 9
6≤x<7 5
7≤x<8 4
8≤x<9 2
请根据不完整的图表中提供的信息解答下列问题:
(1)填空:
①本次调查的样本容量是 50 ;
②频数分布表中a的值为 14 ;
③月均用水量扇形统计图中,分组“E”的扇形圆心角度数是 36° ;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?请说明理由.
【解答】解:(1)①本次调查的样本容量是4÷8%=50;
②频数分布表中a的值为50﹣(4+12+9+5+4+2)=14;
③月均用水量扇形统计图中,分组“E”的扇形圆心角度数是360°36°;
故答案为:50,14,36°;
(2)要使60%的家庭水费支出不受影响,家庭月均用水量应该定为5吨,理由如下:因为月平均用水量不超过5吨的百分比为8%+24%+28%=60%.
19.(8分)如图,∠ABC的边BC和∠DEF的边FE相交于点G,且AB∥FE.
(1)若DE∥BC,∠B=60°,求∠DEF的度数;
(2)按照要求完成以下证明,括号内填写推理的依据.
若∠B+∠DEF=180°,求证:BC∥DE.
证明:∵AB∥FE,
∴ ∠FGB+∠B=180° ( 两直线平行,同旁内角互补 ).
∵∠B+∠E=180°,
∴ ∠FGB=∠E .
∴BC∥DE( 同位角相等,两直线平行 ).
【解答】(1)解:∵AB∥FE,
∴∠FGB+∠B=180°,
∵∠B=60°,
∴∠FGB=120°,
∵DE∥BC,
∴∠DEF=∠FGB=120°;
(2)证明:∵AB∥FE,
∴∠FGB+∠B=180°(两直线平行,同旁内角互补),
∵∠B+∠E=180°,
∴∠FGB=∠E,
∴BC∥DE(同位角相等,两直线平行).
故答案为:∠FGB+∠B=180°;两直线平行,同旁内角互补;
∠FGB=∠E;
同位角相等,两直线平行.
20.(8分)天气晴朗时,一个人能看到大海的最远距离s(单位:千米)可用公式来估计,其中h(单位:米)是眼睛离海平面的高度.
(1)如果小天站在岸边观察,当眼睛离海平面的高度是1.6米时,能看到多远?
(2)若小天登上岸边的一个观望台A,已知小天眼睛离观望台地面的高度是1.6米,他想看到距离岸边大约10千米处的一个货轮B,则观望台至少离海平面高多少米才可以看得见?
【解答】解:(1)因为,
所以25,
所以s=﹣5(舍)或s=5,
答:能看到5千米远;
(2)当s=10时,可得102h,
解得h=6.4,
6.4﹣1.6=4.8(米).
则观望台至少离海平面高为4.8米.
四、解答题(本大题有3小题,共40分,解答要求写出文字说明,证明过程或计算步骤。)
21.(16分)如图是由小正方形组成的网格,△ABC的三个顶点都在小正方形的顶点上,在网格上建立平面直角坐标系.已知A(﹣1,4),B(﹣4,0),C(﹣2,﹣2).
(1)取一点D(3,3),将三角形ABC平移至三角形DEF,其中点A的对应点为D,画出三角形DEF,并求其面积;
(2)在x轴上取一点G(x,0),其中x为整数,且满足x≥﹣4,若使三角形ABG的面积小于10,求点G的坐标;
(3)本小题为多项选择题,有多个选项符合题目要求,要求回答时,全部选对的得满分,选对但不全的视正确答案数相应给分,有选错的得0分.题目如下:
若将三角形ABC向左或向右平移,得到点A的三个对应点M(m,4),点P(2m﹣1,4),点N(n,4),则下列说法正确的是 BCD .
A.当m<1时,点M始终在点P的左边
B.当m>1时,点M始终在点P的左边
C.当m<1且n=﹣2时,存在m的值,使得点N在线段MP上
D.当m>1且n=2时,存在m的值,使得点N在线段MP上
【解答】解:(1)如图:
S△DEF=3×62×21×63×4
=18﹣2﹣3﹣6
=7;
(2)S△ABGBG×4=2BG<10,
∴BG<5,
∵x≥﹣4,
∴G(﹣3,0)或(﹣2,0)或(﹣1,0)或(0,0);
(3)当m>1时,m﹣(2m﹣1)=1﹣m<0,
∴M在P点左侧,
∴当m<1时,M在P点右侧,
故B正确,A错误,
当m<1,n=﹣2时,N(﹣2,4),
∵N在线段MP上,
∴2m﹣1≤﹣2≤m,
∴﹣2≤m,
∴m存在,故C正确,
当m>1,n=2时,N(2,4),
∵N在线段MP上,
∴m≤2≤2m﹣1,
∴m≤2,
∴m存在,故D正确,
综上所述,正确的说法是BCD.
故答案为:BCD.
22.(12分)【阅读理解】在小学,我们知道三角形的三个内角和等于180°,也即是,如图1,三角形ABC中,∠A+∠B+∠C=180°,学习平行线后,只需过点A作BC的平行线DE,就把三角形的三个角“聚合”在一起形成一个平角(∠A+∠B+∠C=∠BAC+∠1+∠2=180°).
【解决问题】应用类似的方法,在图2的四边形ABCD中添加适当的平行线,运用平行线的性质以及平角、周角和对顶角等相关知识求出四边形ABCD的四个内角和(即∠A+∠B+∠C+∠D)的度数,并说明理由(注意:不能直接用三角形的三个内角和等于180°的结论).
【解答】解:∠A+∠B+∠C+∠CDA=360°,
理由:过点D作DE∥AB交BC于点E,过E作EF∥CD交AB于F,
∵EF∥CD,
∴∠BEF=∠C,∠FED=∠CDE,
∴∠BED=∠C+∠CDE,
∵DE∥AB,
∴∠A+∠ADE=180°,∠B+∠BED=180°,
∵∠CDA=∠CDE+∠ADE,
∴∠A+∠B+∠C+∠CDA=∠A+∠B+∠C+∠CDE+∠ADE=∠A+∠B+∠BED+∠ADE=360°.
23.(12分)本学期,教科书在七年级下册第十一章《二元一次方程组》的“阅读与思考”栏目中,介绍了《中国古代著名的一次不定方程组问题》,其中有《张丘建算经》记载的“百鸡问题”,意思是:如果一只公鸡值5个钱,一只母鸡值3个钱,3只小鸡值1个钱,现用100个钱,买了100只鸡,问公鸡、母鸡、小鸡各买了多少只?
小天和小河对此很感兴趣,一起展开了研究,提出以下两个问题.
(1)小天提出的问题是:若公鸡买了8只,则母鸡、小鸡各买了多少只?
(2)小河解答了小天的问题后,找到了一个求解“百鸡问题”的方法:设公鸡、母鸡、小鸡各买了x只,y只,z只,依题意得到方程组,把②×3﹣①,消去z,得到一个二元一次方程7x+4y=100.小河说:“由于是这个二元一次方程的一组解,因此该方程的解可以含字母t的式子表示,即为(t为整数),根据题意,由x,y的取值范围可以求出t的值,由此可求出满足条件的公鸡、母鸡、小鸡的数量情况.
现在,请你先解答小天的问题,然后把小河求解“百鸡问题”的过程补充完整.
【解答】解:(1)设母鸡买了m只,小鸡买了n只,
根据题意得:,
解得:.
答:母鸡买了11只,小鸡买了81只;
(2)设公鸡、母鸡、小鸡各买了x只,y只,z只,
根据题意得:,
(②×3﹣①)÷2得:7x+4y=100,
∵是这个二元一次方程的一组解,
∴该方程的解可以含字母t的式子表示,即为(t为整数),
∵x,y非负,
∴,
解得:25≤t,
又∵t为整数,
∴t可以为25,26,27,28,
当t=25时,x=﹣100+4t=﹣100+4×25=0,y=200﹣7t=200﹣7×25=25,z=100﹣x﹣y=100﹣0﹣25=75;
当t=26时,x=﹣100+4t=﹣100+4×26=4,y=200﹣7t=200﹣7×26=18,z=100﹣x﹣y=100﹣4﹣18=78;
当t=27时,x=﹣100+4t=﹣100+4×27=8,y=200﹣7t=200﹣7×27=11,z=100﹣x﹣y=100﹣8﹣11=81;
当t=28时,x=﹣100+4t=﹣100+4×28=12,y=200﹣7t=200﹣7×28=4,z=100﹣x﹣y=100﹣12﹣4=84.
答:公鸡、母鸡、小鸡各买了0只,25只,75只或4只,18只,78只或8只,11只,81只或12只,4只,84只.
一、单项选择题(本题有10个小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的.)
1.(3分)下列各数中,属于无理数的是( )
A. B.﹣3 C.3.1415926 D.
2.(3分)如图,直线外一点O,点C、D、E、F都在直线AB上,则点O到直线AB的距离是( )
A.线段OC的长度 B.线段OD的长度
C.线段OE的长度 D.线段OF的长度
3.(3分)下列日常使用的工具或学具中,没有应用到对顶角及其相关知识的是( )
A.
B.
C.
D.
4.(3分)在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(3分)若m>n,则下列各式中正确的是( )
A.m+2<n+2 B.m﹣3<n﹣3 C.﹣5m<﹣5n D.
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
7.(3分)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOA=135°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
8.(3分)下列命题中,真命题是( )
A.相等的角是对顶角
B.在同一平面内,垂直于同一条直线的两条直线平行
C.两条直线被第三条直线所截,同位角相等
D.同旁内角互补
9.(3分)如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图案,已知B(2,4),则点A的坐标为( )
A.(4,5) B.(5,5) C.(5,6) D.(6,6)
10.(3分)已知关于x,y的二元一次方程ax+b=y,当x分别取值时对于y的值如表所示,则关于x的不等式ax+b<0的解集为( )
x … ﹣1 0 1 2 3 …
y … 3 2 1 0 ﹣1 …
A.x<0 B.x>0 C.x<2 D.x>2
二、填空题(本题有5个小题,每小题3分,共15分。)
11.(3分)﹣64的立方根是 .
12.(3分)用适当的符号表示不等关系“m与3的和小于5”,则可以得到数学表达式为 .
13.(3分)为了研究气温对冷饮销售的影响,一家饮品店经过一段时间的统计,得到一组卖出的冷饮杯数与当天最高气温的数据,用如图所示的趋势图描述这家饮品店一天中卖出的冷饮杯数与当天的最高气温之间的关系.根据所作的趋势图,估计当一天的最高气温为30℃时,饮品店卖出的冷饮杯数约为 .
14.(3分)仰卧起坐是增加躯干肌肉力量和伸张性的一种运动,能够很好的锻炼腹部肌肉,如图是小美同学做仰卧起坐运动某一瞬间的动作及其示意图,AB∥CD,AC∥DE,点F在直线AC上,∠FAB=120°,∠E=55°,则∠DCE的度数为 .
15.(3分)如图,动点P在平面直角坐标系中按箭头所示方向跳动,第一次从原点O跳动到点P1(1,﹣1),第二次跳动到点P2(2,0),第三次跳动到点P3(3,1),第四次跳动到点P4(4,0),第五次跳动到点P5(5,0),第六次跳动到点P6(6,﹣1)…,按这样的跳动规律,点P2025的坐标是 .
三、解答题(本大题有5小题,共35分,解答要求写出文字说明,证明过程或计算步骤。)
16.(6分)(1)解方程组:;
(2)解不等式:5x+15>3x﹣1.
17.(6分)计算:
(1);
(2).
18.(7分)2025年3月22日是第三十二届“世界水日”,世界水日提醒我们:水是生命之源,需全世界共同行动保护这一珍贵资源.某市在实施居民用水定额管理前,对居民生活用水情况进行调查,通过调查获得了一些家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整统计表和统计图.
月均用水量频数分布表
分组 频数
2≤x<3 4
3≤x<4 12
4≤x<5 a
5≤x<6 9
6≤x<7 5
7≤x<8 4
8≤x<9 2
请根据不完整的图表中提供的信息解答下列问题:
(1)填空:
①本次调查的样本容量是 ;
②频数分布表中a的值为 ;
③月均用水量扇形统计图中,分组“E”的扇形圆心角度数是 ;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?请说明理由.
19.(8分)如图,∠ABC的边BC和∠DEF的边FE相交于点G,且AB∥FE.
(1)若DE∥BC,∠B=60°,求∠DEF的度数;
(2)按照要求完成以下证明,括号内填写推理的依据.
若∠B+∠DEF=180°,求证:BC∥DE.
证明:∵AB∥FE,
∴ ( ).
∵∠B+∠E=180°,
∴ .
∴BC∥DE( ).
20.(8分)天气晴朗时,一个人能看到大海的最远距离s(单位:千米)可用公式来估计,其中h(单位:米)是眼睛离海平面的高度.
(1)如果小天站在岸边观察,当眼睛离海平面的高度是1.6米时,能看到多远?
(2)若小天登上岸边的一个观望台A,已知小天眼睛离观望台地面的高度是1.6米,他想看到距离岸边大约10千米处的一个货轮B,则观望台至少离海平面高多少米才可以看得见?
四、解答题(本大题有3小题,共40分,解答要求写出文字说明,证明过程或计算步骤。)
21.(16分)如图是由小正方形组成的网格,△ABC的三个顶点都在小正方形的顶点上,在网格上建立平面直角坐标系.已知A(﹣1,4),B(﹣4,0),C(﹣2,﹣2).
(1)取一点D(3,3),将三角形ABC平移至三角形DEF,其中点A的对应点为D,画出三角形DEF,并求其面积;
(2)在x轴上取一点G(x,0),其中x为整数,且满足x≥﹣4,若使三角形ABG的面积小于10,求点G的坐标;
(3)本小题为多项选择题,有多个选项符合题目要求,要求回答时,全部选对的得满分,选对但不全的视正确答案数相应给分,有选错的得0分.题目如下:
若将三角形ABC向左或向右平移,得到点A的三个对应点M(m,4),点P(2m﹣1,4),点N(n,4),则下列说法正确的是 .
A.当m<1时,点M始终在点P的左边
B.当m>1时,点M始终在点P的左边
C.当m<1且n=﹣2时,存在m的值,使得点N在线段MP上
D.当m>1且n=2时,存在m的值,使得点N在线段MP上
22.(12分)【阅读理解】在小学,我们知道三角形的三个内角和等于180°,也即是,如图1,三角形ABC中,∠A+∠B+∠C=180°,学习平行线后,只需过点A作BC的平行线DE,就把三角形的三个角“聚合”在一起形成一个平角(∠A+∠B+∠C=∠BAC+∠1+∠2=180°).
【解决问题】应用类似的方法,在图2的四边形ABCD中添加适当的平行线,运用平行线的性质以及平角、周角和对顶角等相关知识求出四边形ABCD的四个内角和(即∠A+∠B+∠C+∠D)的度数,并说明理由(注意:不能直接用三角形的三个内角和等于180°的结论).
23.(12分)本学期,教科书在七年级下册第十一章《二元一次方程组》的“阅读与思考”栏目中,介绍了《中国古代著名的一次不定方程组问题》,其中有《张丘建算经》记载的“百鸡问题”,意思是:如果一只公鸡值5个钱,一只母鸡值3个钱,3只小鸡值1个钱,现用100个钱,买了100只鸡,问公鸡、母鸡、小鸡各买了多少只?
小天和小河对此很感兴趣,一起展开了研究,提出以下两个问题.
(1)小天提出的问题是:若公鸡买了8只,则母鸡、小鸡各买了多少只?
(2)小河解答了小天的问题后,找到了一个求解“百鸡问题”的方法:设公鸡、母鸡、小鸡各买了x只,y只,z只,依题意得到方程组,把②×3﹣①,消去z,得到一个二元一次方程7x+4y=100.小河说:“由于是这个二元一次方程的一组解,因此该方程的解可以含字母t的式子表示,即为(t为整数),根据题意,由x,y的取值范围可以求出t的值,由此可求出满足条件的公鸡、母鸡、小鸡的数量情况.
现在,请你先解答小天的问题,然后把小河求解“百鸡问题”的过程补充完整.
2024-2025学年广东省广州市天河区七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D B C D C B B D
一、单项选择题(本题有10个小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的.)
1.(3分)下列各数中,属于无理数的是( )
A. B.﹣3 C.3.1415926 D.
【解答】解:A、是无理数,故此选项符合题意;
B、﹣3是有理数,故此选项不符合题意;
C、3.1415926是有理数,故此选项不符合题意;
D、是有理数,故此选项不符合题意;
故选:A.
2.(3分)如图,直线外一点O,点C、D、E、F都在直线AB上,则点O到直线AB的距离是( )
A.线段OC的长度 B.线段OD的长度
C.线段OE的长度 D.线段OF的长度
【解答】解:∵直线外一点到直线的垂线段的长度,叫做点到直线的距离,
∴由图可知,点O到直线AB的距离是线段OD的长度.
故选:B.
3.(3分)下列日常使用的工具或学具中,没有应用到对顶角及其相关知识的是( )
A.
B.
C.
D.
【解答】解:选项A,选项B,选项C中的工具,利用了对顶角相等,而选项D利用的是“画一条线段等于已知线段”,
故选:D.
4.(3分)在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:点(﹣5,2)在第二象限.
故选:B.
5.(3分)若m>n,则下列各式中正确的是( )
A.m+2<n+2 B.m﹣3<n﹣3 C.﹣5m<﹣5n D.
【解答】解:A、在不等式m>n的两边同时加上2,不等号方向不变,即m+2>n+2,故本选项不符合题意.
B、在不等式m>n的两边同时减去3,不等号方向不变,即m﹣3>n﹣3,故本选项不符合题意.
C、在不等式m>n的两边同时乘﹣5,不等号方向改变,即﹣5m<﹣5n,故本选项符合题意.
D、在不等式m>n的两边同时除以6,不等号方向不变,即,故本选项不符合题意.
故选:C.
6.(3分)不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
【解答】解:解不等式组得:,
∴不等式组的解集为:﹣1<x≤2,
在数轴上表示如图:
.
故选:D.
7.(3分)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOA=135°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
【解答】解:∵∠DOA=135°,
∴∠DOA=∠BOC=135°,
∵OE⊥AB,
∴∠BOE=90°,
∴∠COE=∠BOC﹣∠BOE=45°,
故选:C.
8.(3分)下列命题中,真命题是( )
A.相等的角是对顶角
B.在同一平面内,垂直于同一条直线的两条直线平行
C.两条直线被第三条直线所截,同位角相等
D.同旁内角互补
【解答】解:A、相等的角不一定是对顶角,故错误,是假命题,不符合题意;
B、在同一平面内,垂直于同一直线的两条直线平行,正确,是真命题,符合题意;
C、两条平行直线被第三条直线所截,同位角相等,故错误,是假命题,不符合题意;
D、两直线平行,同旁内角互补,故错误,是假命题,不符合题意.
故选:B.
9.(3分)如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图案,已知B(2,4),则点A的坐标为( )
A.(4,5) B.(5,5) C.(5,6) D.(6,6)
【解答】解:设长方形纸片的长为a,宽为b,
由B点坐标可以得到:
,
解得:,
∴点A的横坐标为:2×1+3=5,纵坐标为2×1+3=5,
故选:B.
10.(3分)已知关于x,y的二元一次方程ax+b=y,当x分别取值时对于y的值如表所示,则关于x的不等式ax+b<0的解集为( )
x … ﹣1 0 1 2 3 …
y … 3 2 1 0 ﹣1 …
A.x<0 B.x>0 C.x<2 D.x>2
【解答】解:由题意得出,
解得,
则不等式为﹣x+2<0,
解得x>2,
故选:D.
二、填空题(本题有5个小题,每小题3分,共15分。)
11.(3分)﹣64的立方根是 ﹣4 .
【解答】解:∵(﹣4)3=﹣64,
∴﹣64的立方根是﹣4.
故答案为:﹣4.
12.(3分)用适当的符号表示不等关系“m与3的和小于5”,则可以得到数学表达式为 m+3<5 .
【解答】解:由题意得:m+3<5,
故答案为:m+3<5.
13.(3分)为了研究气温对冷饮销售的影响,一家饮品店经过一段时间的统计,得到一组卖出的冷饮杯数与当天最高气温的数据,用如图所示的趋势图描述这家饮品店一天中卖出的冷饮杯数与当天的最高气温之间的关系.根据所作的趋势图,估计当一天的最高气温为30℃时,饮品店卖出的冷饮杯数约为 180 .
【解答】解:趋势图如图所示:
估计当一天的最高气温为30℃时,饮品店卖出的冷饮杯数约为180杯.
故答案为:180.
14.(3分)仰卧起坐是增加躯干肌肉力量和伸张性的一种运动,能够很好的锻炼腹部肌肉,如图是小美同学做仰卧起坐运动某一瞬间的动作及其示意图,AB∥CD,AC∥DE,点F在直线AC上,∠FAB=120°,∠E=55°,则∠DCE的度数为 65° .
【解答】解:∵AB∥CD,
∴∠ACD=∠FAB=120°,
∵AC∥DE,
∴∠ACE=∠E=55°,
∴∠DCE=120°﹣55°=65°.
故答案为:65°.
15.(3分)如图,动点P在平面直角坐标系中按箭头所示方向跳动,第一次从原点O跳动到点P1(1,﹣1),第二次跳动到点P2(2,0),第三次跳动到点P3(3,1),第四次跳动到点P4(4,0),第五次跳动到点P5(5,0),第六次跳动到点P6(6,﹣1)…,按这样的跳动规律,点P2025的坐标是 (2025,0) .
【解答】解:第一次从原点O跳动到点P1(1,﹣1),
第二次跳动到点P2(2,0),
第三次跳动到点P3(3,1),
第四次跳动到点P4(4,0),
第五次跳动到点P5(5,0),
第六次跳动到点P6(6,﹣1),
∴横坐标与所跳次数相同,即跳了n次,该点的横坐标为n,纵坐标每5次一循环,
∴2025÷5=405,
∴P2025(2025,0),
故答案为:(2025,0).
三、解答题(本大题有5小题,共35分,解答要求写出文字说明,证明过程或计算步骤。)
16.(6分)(1)解方程组:;
(2)解不等式:5x+15>3x﹣1.
【解答】解:(1),
①代入②,得:2x+5x+10=3,
解得x=﹣1,
将x=﹣1代入①得:y=1,
所以;
(2)∵5x+15>3x﹣1,
∴5x﹣3x>﹣1﹣15,
2x>﹣16,
则x>﹣8.
17.(6分)计算:
(1);
(2).
【解答】解:(1)
;
(2)
=2+(﹣3)
=﹣1.
18.(7分)2025年3月22日是第三十二届“世界水日”,世界水日提醒我们:水是生命之源,需全世界共同行动保护这一珍贵资源.某市在实施居民用水定额管理前,对居民生活用水情况进行调查,通过调查获得了一些家庭去年的月均用水量(单位:吨).以下是整理数据后的不完整统计表和统计图.
月均用水量频数分布表
分组 频数
2≤x<3 4
3≤x<4 12
4≤x<5 a
5≤x<6 9
6≤x<7 5
7≤x<8 4
8≤x<9 2
请根据不完整的图表中提供的信息解答下列问题:
(1)填空:
①本次调查的样本容量是 50 ;
②频数分布表中a的值为 14 ;
③月均用水量扇形统计图中,分组“E”的扇形圆心角度数是 36° ;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?请说明理由.
【解答】解:(1)①本次调查的样本容量是4÷8%=50;
②频数分布表中a的值为50﹣(4+12+9+5+4+2)=14;
③月均用水量扇形统计图中,分组“E”的扇形圆心角度数是360°36°;
故答案为:50,14,36°;
(2)要使60%的家庭水费支出不受影响,家庭月均用水量应该定为5吨,理由如下:因为月平均用水量不超过5吨的百分比为8%+24%+28%=60%.
19.(8分)如图,∠ABC的边BC和∠DEF的边FE相交于点G,且AB∥FE.
(1)若DE∥BC,∠B=60°,求∠DEF的度数;
(2)按照要求完成以下证明,括号内填写推理的依据.
若∠B+∠DEF=180°,求证:BC∥DE.
证明:∵AB∥FE,
∴ ∠FGB+∠B=180° ( 两直线平行,同旁内角互补 ).
∵∠B+∠E=180°,
∴ ∠FGB=∠E .
∴BC∥DE( 同位角相等,两直线平行 ).
【解答】(1)解:∵AB∥FE,
∴∠FGB+∠B=180°,
∵∠B=60°,
∴∠FGB=120°,
∵DE∥BC,
∴∠DEF=∠FGB=120°;
(2)证明:∵AB∥FE,
∴∠FGB+∠B=180°(两直线平行,同旁内角互补),
∵∠B+∠E=180°,
∴∠FGB=∠E,
∴BC∥DE(同位角相等,两直线平行).
故答案为:∠FGB+∠B=180°;两直线平行,同旁内角互补;
∠FGB=∠E;
同位角相等,两直线平行.
20.(8分)天气晴朗时,一个人能看到大海的最远距离s(单位:千米)可用公式来估计,其中h(单位:米)是眼睛离海平面的高度.
(1)如果小天站在岸边观察,当眼睛离海平面的高度是1.6米时,能看到多远?
(2)若小天登上岸边的一个观望台A,已知小天眼睛离观望台地面的高度是1.6米,他想看到距离岸边大约10千米处的一个货轮B,则观望台至少离海平面高多少米才可以看得见?
【解答】解:(1)因为,
所以25,
所以s=﹣5(舍)或s=5,
答:能看到5千米远;
(2)当s=10时,可得102h,
解得h=6.4,
6.4﹣1.6=4.8(米).
则观望台至少离海平面高为4.8米.
四、解答题(本大题有3小题,共40分,解答要求写出文字说明,证明过程或计算步骤。)
21.(16分)如图是由小正方形组成的网格,△ABC的三个顶点都在小正方形的顶点上,在网格上建立平面直角坐标系.已知A(﹣1,4),B(﹣4,0),C(﹣2,﹣2).
(1)取一点D(3,3),将三角形ABC平移至三角形DEF,其中点A的对应点为D,画出三角形DEF,并求其面积;
(2)在x轴上取一点G(x,0),其中x为整数,且满足x≥﹣4,若使三角形ABG的面积小于10,求点G的坐标;
(3)本小题为多项选择题,有多个选项符合题目要求,要求回答时,全部选对的得满分,选对但不全的视正确答案数相应给分,有选错的得0分.题目如下:
若将三角形ABC向左或向右平移,得到点A的三个对应点M(m,4),点P(2m﹣1,4),点N(n,4),则下列说法正确的是 BCD .
A.当m<1时,点M始终在点P的左边
B.当m>1时,点M始终在点P的左边
C.当m<1且n=﹣2时,存在m的值,使得点N在线段MP上
D.当m>1且n=2时,存在m的值,使得点N在线段MP上
【解答】解:(1)如图:
S△DEF=3×62×21×63×4
=18﹣2﹣3﹣6
=7;
(2)S△ABGBG×4=2BG<10,
∴BG<5,
∵x≥﹣4,
∴G(﹣3,0)或(﹣2,0)或(﹣1,0)或(0,0);
(3)当m>1时,m﹣(2m﹣1)=1﹣m<0,
∴M在P点左侧,
∴当m<1时,M在P点右侧,
故B正确,A错误,
当m<1,n=﹣2时,N(﹣2,4),
∵N在线段MP上,
∴2m﹣1≤﹣2≤m,
∴﹣2≤m,
∴m存在,故C正确,
当m>1,n=2时,N(2,4),
∵N在线段MP上,
∴m≤2≤2m﹣1,
∴m≤2,
∴m存在,故D正确,
综上所述,正确的说法是BCD.
故答案为:BCD.
22.(12分)【阅读理解】在小学,我们知道三角形的三个内角和等于180°,也即是,如图1,三角形ABC中,∠A+∠B+∠C=180°,学习平行线后,只需过点A作BC的平行线DE,就把三角形的三个角“聚合”在一起形成一个平角(∠A+∠B+∠C=∠BAC+∠1+∠2=180°).
【解决问题】应用类似的方法,在图2的四边形ABCD中添加适当的平行线,运用平行线的性质以及平角、周角和对顶角等相关知识求出四边形ABCD的四个内角和(即∠A+∠B+∠C+∠D)的度数,并说明理由(注意:不能直接用三角形的三个内角和等于180°的结论).
【解答】解:∠A+∠B+∠C+∠CDA=360°,
理由:过点D作DE∥AB交BC于点E,过E作EF∥CD交AB于F,
∵EF∥CD,
∴∠BEF=∠C,∠FED=∠CDE,
∴∠BED=∠C+∠CDE,
∵DE∥AB,
∴∠A+∠ADE=180°,∠B+∠BED=180°,
∵∠CDA=∠CDE+∠ADE,
∴∠A+∠B+∠C+∠CDA=∠A+∠B+∠C+∠CDE+∠ADE=∠A+∠B+∠BED+∠ADE=360°.
23.(12分)本学期,教科书在七年级下册第十一章《二元一次方程组》的“阅读与思考”栏目中,介绍了《中国古代著名的一次不定方程组问题》,其中有《张丘建算经》记载的“百鸡问题”,意思是:如果一只公鸡值5个钱,一只母鸡值3个钱,3只小鸡值1个钱,现用100个钱,买了100只鸡,问公鸡、母鸡、小鸡各买了多少只?
小天和小河对此很感兴趣,一起展开了研究,提出以下两个问题.
(1)小天提出的问题是:若公鸡买了8只,则母鸡、小鸡各买了多少只?
(2)小河解答了小天的问题后,找到了一个求解“百鸡问题”的方法:设公鸡、母鸡、小鸡各买了x只,y只,z只,依题意得到方程组,把②×3﹣①,消去z,得到一个二元一次方程7x+4y=100.小河说:“由于是这个二元一次方程的一组解,因此该方程的解可以含字母t的式子表示,即为(t为整数),根据题意,由x,y的取值范围可以求出t的值,由此可求出满足条件的公鸡、母鸡、小鸡的数量情况.
现在,请你先解答小天的问题,然后把小河求解“百鸡问题”的过程补充完整.
【解答】解:(1)设母鸡买了m只,小鸡买了n只,
根据题意得:,
解得:.
答:母鸡买了11只,小鸡买了81只;
(2)设公鸡、母鸡、小鸡各买了x只,y只,z只,
根据题意得:,
(②×3﹣①)÷2得:7x+4y=100,
∵是这个二元一次方程的一组解,
∴该方程的解可以含字母t的式子表示,即为(t为整数),
∵x,y非负,
∴,
解得:25≤t,
又∵t为整数,
∴t可以为25,26,27,28,
当t=25时,x=﹣100+4t=﹣100+4×25=0,y=200﹣7t=200﹣7×25=25,z=100﹣x﹣y=100﹣0﹣25=75;
当t=26时,x=﹣100+4t=﹣100+4×26=4,y=200﹣7t=200﹣7×26=18,z=100﹣x﹣y=100﹣4﹣18=78;
当t=27时,x=﹣100+4t=﹣100+4×27=8,y=200﹣7t=200﹣7×27=11,z=100﹣x﹣y=100﹣8﹣11=81;
当t=28时,x=﹣100+4t=﹣100+4×28=12,y=200﹣7t=200﹣7×28=4,z=100﹣x﹣y=100﹣12﹣4=84.
答:公鸡、母鸡、小鸡各买了0只,25只,75只或4只,18只,78只或8只,11只,81只或12只,4只,84只.
同课章节目录
