海南省西南部分学校2024-2025学年七年级下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 海南省西南部分学校2024-2025学年七年级下学期期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 14:10:22 | ||
图片预览




文档简介
海南省西南部分学校2024-2025学年七年级下学期期末考试数学试题
一、单选题
1.的相反数是( )
A. B. C. D.
2.“一寸光阴一寸金,寸金难买寸光阴.”我们一定要珍惜每分每秒,努力学习,一天的时间为86400秒,将86400用科学记数法表示为( )
A. B. C. D.
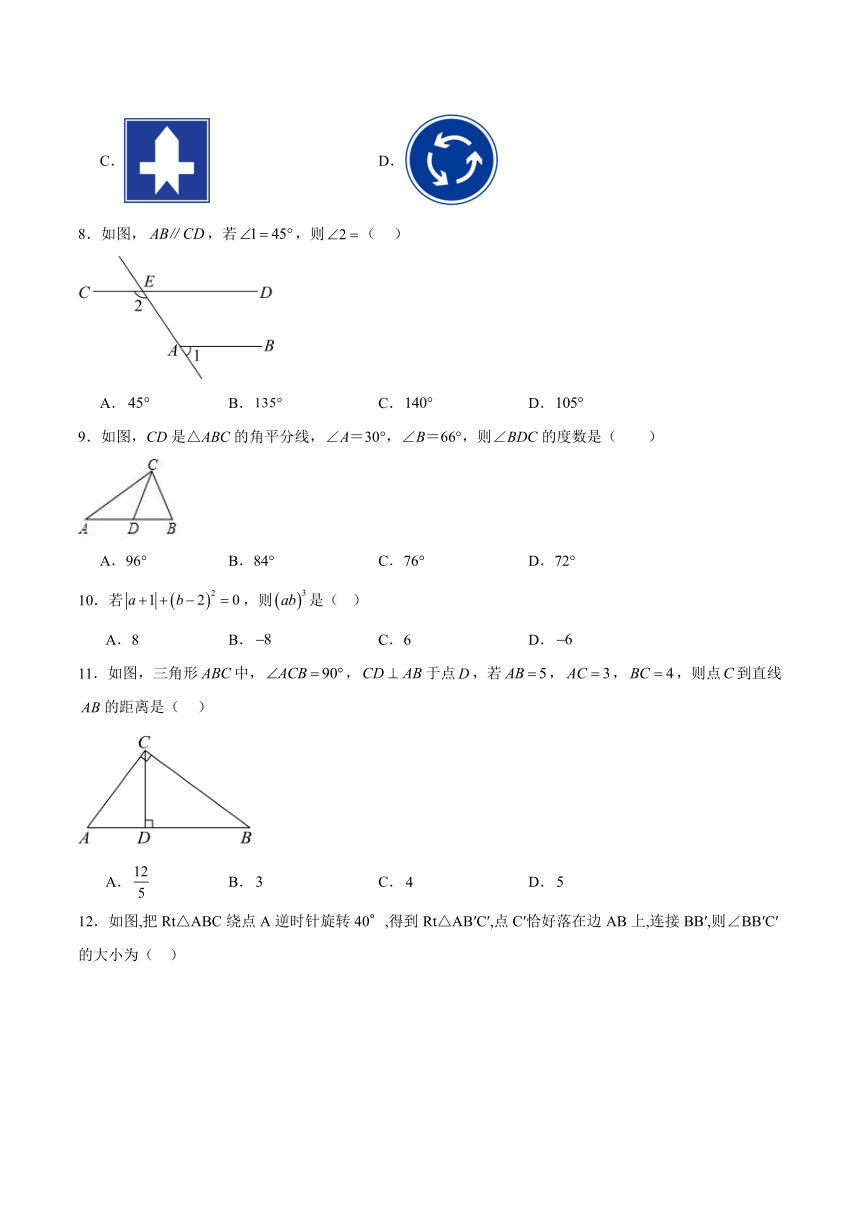
3.如图是由5个小正方体组合成的几何体,则其俯视图为( )
A. B. C. D.
4.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
5.当x=1时,代数式2x+5的值为( )
A.3 B.5 C.7 D.-2
6.如果单项式﹣3xm+3yn和x5y3是同类项,那么m+n的值为( )
A.2 B.3 C.5 D.8
7.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
8.如图,,若,则( )
A. B. C. D.
9.如图,CD是△ABC的角平分线,∠A=30°,∠B=66°,则∠BDC的度数是( )
A.96° B.84° C.76° D.72°
10.若,则是( )
A.8 B. C.6 D.
11.如图,三角形中,,于点,若,,,则点到直线的距离是( )
A. B. C. D.
12.如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′的大小为( )
A.10° B.15° C.20° D.30°
二、填空题
13.已知,则 (填“>”、“<”或“=”号).
14.若正多边形的一个内角等于140°,则这个正多边形的边数是 .
15.等腰三角形ABC的周长是8cm,AB=3cm,则底边长是 cm
16.已知点在直线上,,平分.
(1)如图1,若,则的度数是 .
(2)如图2,若,则的度数是 (用含的代数式表示).
三、解答题
17.计算
(1);
(2)解不等式组,并写出它的所有负整数解.
18.解下列方程(组)
(1);
(2).
19.国漫之光《哪吒之魔童闹海》已连续创造多项纪录,成为全球动画电影票房榜首.某商家决定购进“哪吒”、“敖丙”两种纪念品进行销售,若购进“哪吒”纪念品1件和“敖丙”纪念品2件共需要70元;若购进“哪吒”纪念品3件和“敖丙”纪念品1件共需要110元.
(1)求购进“哪吒”、“敖丙”两种纪念品每件各需要多少元?
(2)该商场计划用不超过3100元的资金购进“哪吒”、“敖丙”两种纪念品共120件,求最多购进“哪吒”纪念品多少件?
20.如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把进行平移, 得到, 使点A与对应, 请在网格中画出
(2)线段与线段的位置关系是 ;(填“平行”或“相交” )
(3)求出的面积.
21.完成推理填空.
已知:如图,,平分,与相交于点,交的延长线于点,,试说明:.
证明:因为(已知)
所以( )
又因为平分( )
所以 (角平分线定义)
所以( )
因为.(已知)
所以 (等量代换)
所以( )
22.【提出问题】若两个角的两边分别平行,则这两个角有怎样的数量关系?
【解决问题】
分两种情况进行探究,请结合如图探究这两个角的数量关系.
(1)第一种:如图①,,,求证:(不需要证明).
第二种:如图②,,,求证:(写出证明过程).
【得出结论】
(2)由(1)我们可以得出结论:若两个角的两边分别平行,则这两个角的数量关系为______.
【拓展应用】
(3)若两个角的两边分别平行,其中一个角比另一个角的2倍少,求这两个角的度数.
(4)同一平面内,两个角的两边分别垂直,当其中的一个角为时,直接写出另一个角的度数.
参考答案
1.D
解:的相反数是2.
故选:D
2.C
解:86400用科学记数法表示为.
故选:C.
3.A
解:从该组合体的俯视图看从左至右共有三列,从左到右第一列有一个正方形,第二列有一个正方形,第三列有两个正方形,可得只有选项A符合题意.
故选:A.
4.A
解:,
,
∴,
将解集表示在数轴上如下:
故选:A.
5.C
解:当x=1时,2x+5=2×1+5=7.
故选C.
6.C
解:∵单项式﹣3xm+3yn和﹣ x5y3是同类项,
∴m+3=5,n=3,
∴m=2,n=3,
∴m+n=5.
故选C.
7.A
根据轴对称图形和中心对称图形的定义可知:A即是轴对称图形又是中心对称图形,所以A正确;B是轴对称图形但不是中心对称图形,所以B错误;C是轴对称图形但不是中心对称图形,所以C错误;D即不是轴对称图形又不是中心对称图形,所以D错误;故选A.
8.B
解:,
,
,
故选:B.
9.D
解:∵∠A=30°,∠B=66°,
∴∠ACB=180°﹣30°﹣66°=84°,
∵CD是△ABC的角平分线,
∴∠ACD=∠ACB=×84°=42°.
∴∠BDC=∠A+∠ACD=30°+42°=72°.
故选:D.
10.B
∵
∴,,
∴,,
∴.
故选:B.
11.A
解:在中,,根据三角形面积公式高,
.
,,
.
,
.
.
解得.
点到直线的距离是.
故选:A.
12.C
∵Rt△ABC旋转得到Rt△AB′C,点C′落在AB上,
∴AB=AB′,∠AC′B′=∠C=90°,
∴∠ABB′=(180° ∠BAB′)= (180° 40°)=70°
∴∠BB′C′=90° ∠ABB′=90° 70°=20°
故选C.
13.
解:,
,
故答案为:.
14.9
∵正多边形的一个内角是140°,
∴它的一个外角是:180°-140°=40°,
∵多边形的外角和为360°,
∴这个正多边形的边数是:360°÷40°=9.
故答案为:9.
15.3或2
解:(1)当AB=3cm为底边时,AC,BC为腰,
由等腰三角形的性质,得AC=BC= (8-AB)=2.5cm,可以围成三角形;
此时底边AB是3cm;
(2)当AB=3cm为腰时,
①若BC为腰,则BC=AB=3cm,底边AC=2 cm,可以围成三角形;
②若BC为底,则AC=AB=3 cm, 底边BC=8-2AB=2cm,可以围成三角形;
此时底边是2cm;
故答案为3或2.
16.
(1)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
故答案为:.
(2)解:∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
故答案为:.
17.(1)9
(2),负整数解有.
(1)解:
(2)解:,
解①得
解②得
∴不等式组的解集为
∴不等式组的负整数解有:
18.(1)
(2)
(1)解:去分母,得,
去括号,得,
移项合并同类项,得;
(2)解:
得,
解得,
将代入得,
解得,
∴.
19.(1)每件“哪吒”纪念品的进价是30元,每件“敖丙”纪念品的进价是20元
(2)最多购进“哪吒”纪念品70件
(1)解:设每件“哪吒”纪念品的进价是x元,每件“敖丙”纪念品的进价是y元,
根据题意得:,
解得:.
答:每件“哪吒”纪念品的进价是30元,每件“敖丙”纪念品的进价是20元;
(2)解;设购进“哪吒”纪念品m件,则“敖丙”纪念品件,
根据题意得:,
解得:,
∴m的最大值为70.
答:最多购进“哪吒”纪念品70件.
20.(1)见解析
(2)平行
(3)
(1)解;如图所示,即为所求;
(2)解:由平移的性质可得线段与线段的位置关系是平行;
(3)解:由题意得,.
21.两直线平行,同位角相等;已知;2;等量代换;2;内错角相等,两直线平行
证明:因为(已知)
所以(两直线平行,同位角相等)
又因为平分(已知)
所以(角平分线定义)
所以(等量代换)
因为.(已知)
所以(等量代换)
所以(内错角相等,两直线平行)
故答案为:两直线平行,同位角相等;已知;2;等量代换;2;内错角相等,两直线平行.
22.()证明见解析;()相等或互补;()两个角为,或,;()或
()证明:∵,
∴,
∵,
∴,
∵,
∴;
()解:由()我们可以得出结论:若两个角的两边分别平行,则这两个角的数量关系为:相等或互补,
故答案为:相等或互补;
()解:设其中一个角为,则另一个角为,
∴当,
解得:,
此时两个角为,;
当,
解得:,
此时两个角为,;
综上可知:两个角为,或,;
()解:如图,
∵,,
∴,
∴;
如图,
∵,,
∴,
∵,
∴.
一、单选题
1.的相反数是( )
A. B. C. D.
2.“一寸光阴一寸金,寸金难买寸光阴.”我们一定要珍惜每分每秒,努力学习,一天的时间为86400秒,将86400用科学记数法表示为( )
A. B. C. D.
3.如图是由5个小正方体组合成的几何体,则其俯视图为( )
A. B. C. D.
4.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
5.当x=1时,代数式2x+5的值为( )
A.3 B.5 C.7 D.-2
6.如果单项式﹣3xm+3yn和x5y3是同类项,那么m+n的值为( )
A.2 B.3 C.5 D.8
7.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
8.如图,,若,则( )
A. B. C. D.
9.如图,CD是△ABC的角平分线,∠A=30°,∠B=66°,则∠BDC的度数是( )
A.96° B.84° C.76° D.72°
10.若,则是( )
A.8 B. C.6 D.
11.如图,三角形中,,于点,若,,,则点到直线的距离是( )
A. B. C. D.
12.如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′的大小为( )
A.10° B.15° C.20° D.30°
二、填空题
13.已知,则 (填“>”、“<”或“=”号).
14.若正多边形的一个内角等于140°,则这个正多边形的边数是 .
15.等腰三角形ABC的周长是8cm,AB=3cm,则底边长是 cm
16.已知点在直线上,,平分.
(1)如图1,若,则的度数是 .
(2)如图2,若,则的度数是 (用含的代数式表示).
三、解答题
17.计算
(1);
(2)解不等式组,并写出它的所有负整数解.
18.解下列方程(组)
(1);
(2).
19.国漫之光《哪吒之魔童闹海》已连续创造多项纪录,成为全球动画电影票房榜首.某商家决定购进“哪吒”、“敖丙”两种纪念品进行销售,若购进“哪吒”纪念品1件和“敖丙”纪念品2件共需要70元;若购进“哪吒”纪念品3件和“敖丙”纪念品1件共需要110元.
(1)求购进“哪吒”、“敖丙”两种纪念品每件各需要多少元?
(2)该商场计划用不超过3100元的资金购进“哪吒”、“敖丙”两种纪念品共120件,求最多购进“哪吒”纪念品多少件?
20.如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把进行平移, 得到, 使点A与对应, 请在网格中画出
(2)线段与线段的位置关系是 ;(填“平行”或“相交” )
(3)求出的面积.
21.完成推理填空.
已知:如图,,平分,与相交于点,交的延长线于点,,试说明:.
证明:因为(已知)
所以( )
又因为平分( )
所以 (角平分线定义)
所以( )
因为.(已知)
所以 (等量代换)
所以( )
22.【提出问题】若两个角的两边分别平行,则这两个角有怎样的数量关系?
【解决问题】
分两种情况进行探究,请结合如图探究这两个角的数量关系.
(1)第一种:如图①,,,求证:(不需要证明).
第二种:如图②,,,求证:(写出证明过程).
【得出结论】
(2)由(1)我们可以得出结论:若两个角的两边分别平行,则这两个角的数量关系为______.
【拓展应用】
(3)若两个角的两边分别平行,其中一个角比另一个角的2倍少,求这两个角的度数.
(4)同一平面内,两个角的两边分别垂直,当其中的一个角为时,直接写出另一个角的度数.
参考答案
1.D
解:的相反数是2.
故选:D
2.C
解:86400用科学记数法表示为.
故选:C.
3.A
解:从该组合体的俯视图看从左至右共有三列,从左到右第一列有一个正方形,第二列有一个正方形,第三列有两个正方形,可得只有选项A符合题意.
故选:A.
4.A
解:,
,
∴,
将解集表示在数轴上如下:
故选:A.
5.C
解:当x=1时,2x+5=2×1+5=7.
故选C.
6.C
解:∵单项式﹣3xm+3yn和﹣ x5y3是同类项,
∴m+3=5,n=3,
∴m=2,n=3,
∴m+n=5.
故选C.
7.A
根据轴对称图形和中心对称图形的定义可知:A即是轴对称图形又是中心对称图形,所以A正确;B是轴对称图形但不是中心对称图形,所以B错误;C是轴对称图形但不是中心对称图形,所以C错误;D即不是轴对称图形又不是中心对称图形,所以D错误;故选A.
8.B
解:,
,
,
故选:B.
9.D
解:∵∠A=30°,∠B=66°,
∴∠ACB=180°﹣30°﹣66°=84°,
∵CD是△ABC的角平分线,
∴∠ACD=∠ACB=×84°=42°.
∴∠BDC=∠A+∠ACD=30°+42°=72°.
故选:D.
10.B
∵
∴,,
∴,,
∴.
故选:B.
11.A
解:在中,,根据三角形面积公式高,
.
,,
.
,
.
.
解得.
点到直线的距离是.
故选:A.
12.C
∵Rt△ABC旋转得到Rt△AB′C,点C′落在AB上,
∴AB=AB′,∠AC′B′=∠C=90°,
∴∠ABB′=(180° ∠BAB′)= (180° 40°)=70°
∴∠BB′C′=90° ∠ABB′=90° 70°=20°
故选C.
13.
解:,
,
故答案为:.
14.9
∵正多边形的一个内角是140°,
∴它的一个外角是:180°-140°=40°,
∵多边形的外角和为360°,
∴这个正多边形的边数是:360°÷40°=9.
故答案为:9.
15.3或2
解:(1)当AB=3cm为底边时,AC,BC为腰,
由等腰三角形的性质,得AC=BC= (8-AB)=2.5cm,可以围成三角形;
此时底边AB是3cm;
(2)当AB=3cm为腰时,
①若BC为腰,则BC=AB=3cm,底边AC=2 cm,可以围成三角形;
②若BC为底,则AC=AB=3 cm, 底边BC=8-2AB=2cm,可以围成三角形;
此时底边是2cm;
故答案为3或2.
16.
(1)解:∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
故答案为:.
(2)解:∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
故答案为:.
17.(1)9
(2),负整数解有.
(1)解:
(2)解:,
解①得
解②得
∴不等式组的解集为
∴不等式组的负整数解有:
18.(1)
(2)
(1)解:去分母,得,
去括号,得,
移项合并同类项,得;
(2)解:
得,
解得,
将代入得,
解得,
∴.
19.(1)每件“哪吒”纪念品的进价是30元,每件“敖丙”纪念品的进价是20元
(2)最多购进“哪吒”纪念品70件
(1)解:设每件“哪吒”纪念品的进价是x元,每件“敖丙”纪念品的进价是y元,
根据题意得:,
解得:.
答:每件“哪吒”纪念品的进价是30元,每件“敖丙”纪念品的进价是20元;
(2)解;设购进“哪吒”纪念品m件,则“敖丙”纪念品件,
根据题意得:,
解得:,
∴m的最大值为70.
答:最多购进“哪吒”纪念品70件.
20.(1)见解析
(2)平行
(3)
(1)解;如图所示,即为所求;
(2)解:由平移的性质可得线段与线段的位置关系是平行;
(3)解:由题意得,.
21.两直线平行,同位角相等;已知;2;等量代换;2;内错角相等,两直线平行
证明:因为(已知)
所以(两直线平行,同位角相等)
又因为平分(已知)
所以(角平分线定义)
所以(等量代换)
因为.(已知)
所以(等量代换)
所以(内错角相等,两直线平行)
故答案为:两直线平行,同位角相等;已知;2;等量代换;2;内错角相等,两直线平行.
22.()证明见解析;()相等或互补;()两个角为,或,;()或
()证明:∵,
∴,
∵,
∴,
∵,
∴;
()解:由()我们可以得出结论:若两个角的两边分别平行,则这两个角的数量关系为:相等或互补,
故答案为:相等或互补;
()解:设其中一个角为,则另一个角为,
∴当,
解得:,
此时两个角为,;
当,
解得:,
此时两个角为,;
综上可知:两个角为,或,;
()解:如图,
∵,,
∴,
∴;
如图,
∵,,
∴,
∵,
∴.
同课章节目录
