河南省洛阳市伊川县2024-2025学年八年级下学期6月期末考试数学试卷(含解析)
文档属性
| 名称 | 河南省洛阳市伊川县2024-2025学年八年级下学期6月期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 135.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 14:10:34 | ||
图片预览



文档简介
2024-2025学年河南省洛阳市伊川县八年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若关于的方程有增根,则增根为( )
A. B. C. D.
2.年月日华为公司上市的手机搭载的是自主研发的麒麟处理器,这款处理器是华为采用制程技术的手机芯片,,其中用科学记数法表示为
A. B. C. D.
3.如图,用绳子围成周长为的矩形,记矩形的一边长为,它的邻边长为则关于的函数解析式是( )
A. B. C. D.
4.一组数据,,,,的平均数是,另一组数据,,,,的平均数是( )
A. B. C. D.
5.与直线关于轴对称的直线经过点,则的值为( )
A. B. C. D.
6.如图,在平行四边形中,::,则的度数为( )
A.
B.
C.
D.
7.如图是一块大正方形地板砖,其图案是由四个全等的五边形和一个小正方形组成,若大正方形地板砖的边长为,是的中点,则图案中小正方形的边长为( )
A.
B.
C.
D.
8.数据分析是从数据中获取有效信息的重要手段请根据如下某组数据的方差计算式:你不能得到的有效信息是( )
A. 这组数据的中位数是 B. 这组数据的平均数是
C. 这组数据的众数是 D. 这组数据的方差是
9.如图,在中,,点从点出发沿边向点运动,运动到点停止,过点分别作交于点,交于点,则四边形形状的变化依次为( )
A. 矩形菱形矩形 B. 矩形正方形矩形
C. 平行四边形菱形平行四边形 D. 平行四边形正方形平行四边形
10.如图,直线分别与轴、轴交于,两点,以为边作正方形,双曲线经过点,则的值为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.计算:______.
12.将直线向上平移个单位长度后,得到的新直线的解析式是______.
13.某校规定学生的数学成绩由三部分组成,平时成绩占,期中考试成绩占,期末考试成绩占,若小晓同学的三项成绩分别是分,分,分,则小晓同学本学期的数学成绩应记为______分
14.如图,在平面直角坐标系中,过点分别作轴于点,轴于点,反比例函数的图象分别与,相交于,两点,连接,若四边形的面积为,则的值为______.
15.方胜纹是中国传统纹样,寓意吉祥如图是一个刻有方胜纹的方胜盘,图是方胜盘的示意图,菱形与菱形是完全相同的两个菱形,中间四边形也是菱形,若,,,为的中点,则四边形的面积为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
化简:.
17.本小题分
中华优秀传统文化源远流长、是中华文明的智慧结晶孙子算经周髀算经是我国古代较为普及的算书,书中许多问题浅显有趣某书店的孙子算经单价是周髀算经单价的,用元购买孙子算经比购买周髀算经多买本求两种图书的单价分别为多少元.
18.本小题分
如图,已知四边形中,,,求证:四边形是平行四边形.
19.本小题分
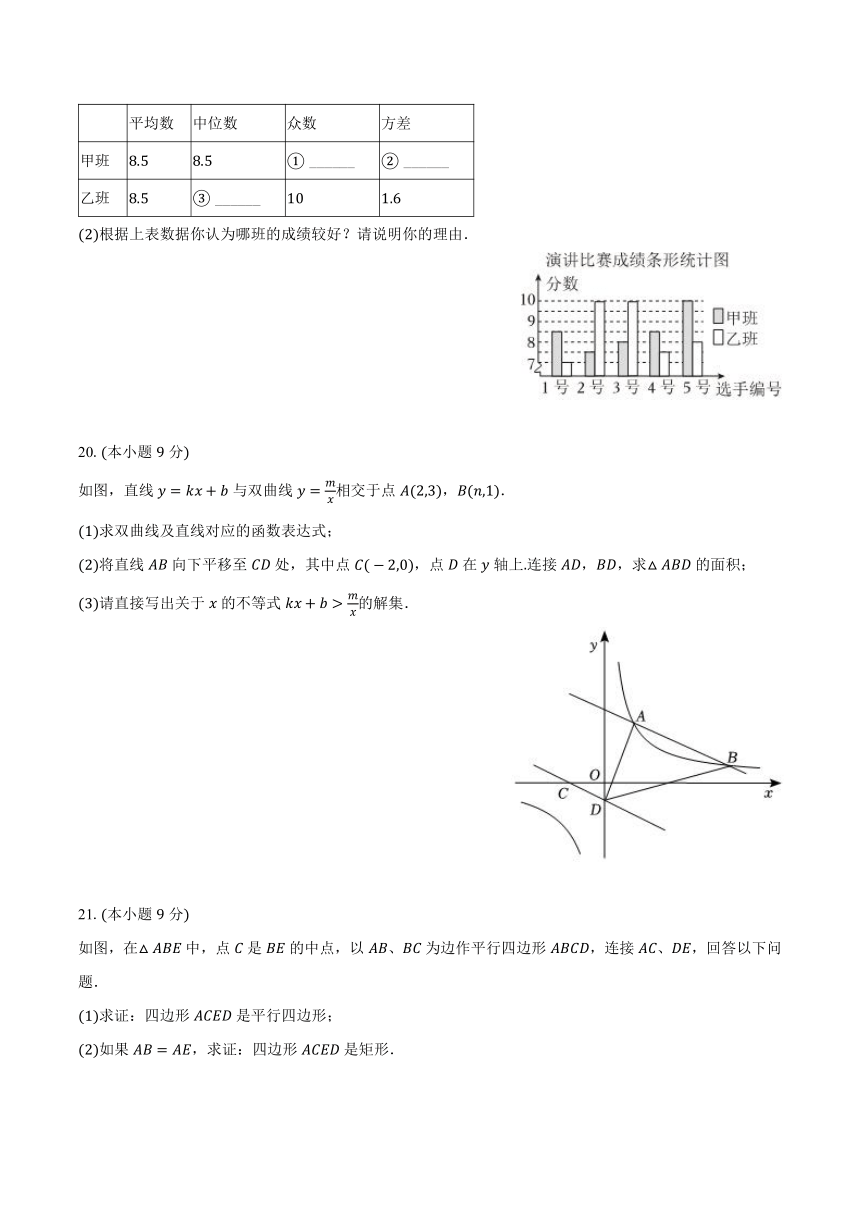
某中学八年级甲、乙两班分别选名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示.
根据图中数据填写如表:
平均数 中位数 众数 方差
甲班 ______ ______
乙班 ______
根据上表数据你认为哪班的成绩较好?请说明你的理由.
20.本小题分
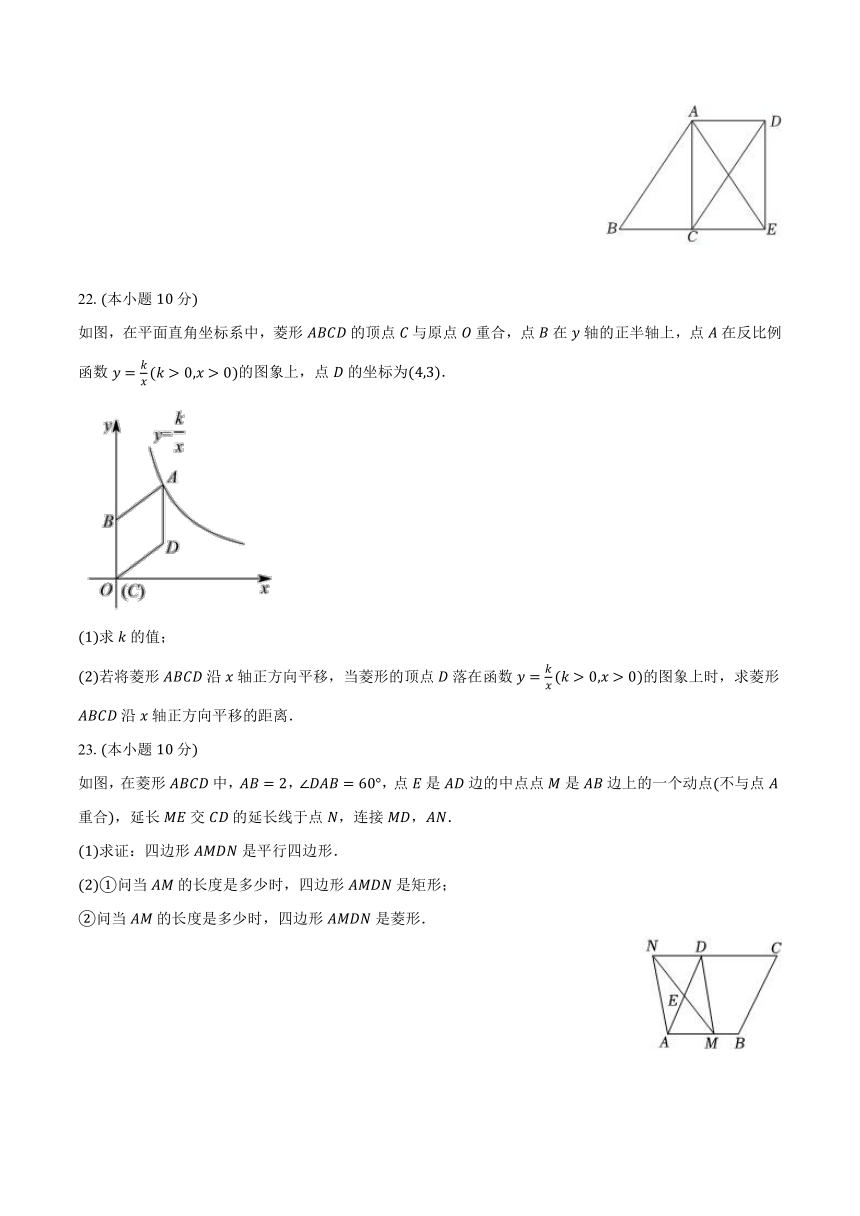
如图,直线与双曲线相交于点,.
求双曲线及直线对应的函数表达式;
将直线向下平移至处,其中点,点在轴上连接,,求的面积;
请直接写出关于的不等式的解集.
21.本小题分
如图,在中,点是的中点,以、为边作平行四边形,连接、,回答以下问题.
求证:四边形是平行四边形;
如果,求证:四边形是矩形.
22.本小题分
如图,在平面直角坐标系中,菱形的顶点与原点重合,点在轴的正半轴上,点在反比例函数的图象上,点的坐标为.
求的值;
若将菱形沿轴正方向平移,当菱形的顶点落在函数的图象上时,求菱形沿轴正方向平移的距离.
23.本小题分
如图,在菱形中,,,点是边的中点点是边上的一个动点不与点重合,延长交的延长线于点,连接,.
求证:四边形是平行四边形.
问当的长度是多少时,四边形是矩形;
问当的长度是多少时,四边形是菱形.
答案和解析
1.
解:最简公分母是,原方程有增根,
最简公分母,
增根是.
故选:.
2.
解:,
故选:.
3.
解:由题意得,,
,
,
关于的函数解析式是,
故选:.
4.
解:这组数据,,,,的平均数是:
根据,,,,的平均数是,
,
,
把代入得:
,
.
故选:.
5.
解:与直线关于轴对称的点的坐标为横坐标互为相反数,纵坐标不变,则,即.
经过点,
,
,
故选:.
6.
解:四边形是平行四边形,
,,
,,
在平行四边形中,::,
,
,
,
,
故选:.
7.
解:设,、、为大正方形的三个顶点,、为五边形的顶点,则,
大正方形由四个全等的五边形和一个小正方形组成,大正方形的边长为,
,,,,
四边形是矩形,
,,
,,且,
,
,
,
是的中点,
,
,
解得,
小正方形的边长为,
故选:.
8.
解:根据方差公式可得这一组数据为,,,,,
A、这组数据的中位数是,原选项不符合题意;
B、这组数据的平均数是,原选项不符合题意;
C、由于出现次数最多,则这组数据的众数是,原选项不符合题意;
D、这组数据的平均数是,
,
原选项符合题意;
故选:.
9.
解:,,
四边形是平行四边形,
,
平行四边形是矩形,
在点的运动过程中,四边形始终是矩形,
当时,矩形是正方形,
四边形形状的变化依次为:矩形正方形矩形.
故选:.
10.
解:对于,当时,,当时,,
点,点,
,,
过点作于点,如下图所示:
,,
四边形为正方形,
,,
,
,
在和中,
,
≌,
,,
,
点的坐标为,
双曲线经过点,
.
故选:.
11.
解:原式.
故答案为:.
12.
解:将直线向上平移个单位长度,得到的新直线的解析式为:.
故答案为:.
13.
解:小晓同学本学期的数学成绩应记为分,
故答案为:.
14.
解:点,作轴于点,轴于点,
,
点、在反比例函数图象上,
.
反比例函数图象在第二象限,
.
故答案为:.
15.
解:在菱形中,,,
,
,
为的中点,
,
菱形的面积,
故答案为:.
16.;
.
原式
;
原式
.
17.解:设周髀算经单价为元,则孙子算经单价为元.
依题意得,
解得.
经检验,是原方程的解,且符合题意,
元.
答:周髀算经单价为元,孙子算经单价为元.
18.证明:,,,
,
又,
,
,,
四边形是平行四边形两组对边分别平行的四边形是平行四边形.
19.,,;
答案不唯一,只要言之有理即可,具体见解答.
解:甲班个数据中出现了次,是出现次数最多的数据,
甲班成绩的众数为:;
甲班成绩的方差为:;
乙班成绩由小到大排列为:,,,,,处在中间的数据是,
乙班成绩的中位数为:,
故答案为:,,;
答案不唯一,只要言之有理即可,比如:
从平均数看,两班成绩的平均线相同,则甲、乙成绩一样好;
从中位数看,甲班成绩的中位数高,故甲班的成绩好;
从方差看,甲班的方差小,成绩稳定,故甲班的成绩好.
20.解:将代入双曲线,
,
双曲线的解析式为,
将点代入,
,
,
将,代入,
,
解得,
直线解析式为;
直线向下平移至,
,
设直线的解析式为,
将点代入,
,
解得,
直线的解析式为,
,
过点作交于,
设直线与轴的交点为,与轴的交点为,
,,
,,
,
,,
,
,
,
,
,
,
的面积;
由图可知时,.
21.见解析过程;
见解析过程.
证明:四边形是平行四边形,
,,
点是的中点,
,
,
且,
四边形是平行四边形;
,点是的中点,
,
四边形是矩形.
22.解:过点作轴的垂线,垂足为,
点的坐标为,
,,
,
,
点坐标为,
,
;
将菱形沿轴正方向平移,使得点落在函数的图象点处,
过点做轴的垂线,垂足为.
,
,
点的纵坐标为,
点在的图象上
,
解得:,
即,
,
菱形平移的距离为.
23.证明:四边形是菱形,
,
,,
又点是边的中点
,
≌,
,
四边形是平行四边形;
解:当的值为时,四边形是矩形.
理由如下:
,
点是边的中点,
,
,
是等边三角形,
,,
,
,即,
平行四边形是矩形.
故答案为:
当的值为时,四边形是菱形.
理由如下:
,
,
,
是等边三角形,
,
平行四边形是菱形.
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若关于的方程有增根,则增根为( )
A. B. C. D.
2.年月日华为公司上市的手机搭载的是自主研发的麒麟处理器,这款处理器是华为采用制程技术的手机芯片,,其中用科学记数法表示为
A. B. C. D.
3.如图,用绳子围成周长为的矩形,记矩形的一边长为,它的邻边长为则关于的函数解析式是( )
A. B. C. D.
4.一组数据,,,,的平均数是,另一组数据,,,,的平均数是( )
A. B. C. D.
5.与直线关于轴对称的直线经过点,则的值为( )
A. B. C. D.
6.如图,在平行四边形中,::,则的度数为( )
A.
B.
C.
D.
7.如图是一块大正方形地板砖,其图案是由四个全等的五边形和一个小正方形组成,若大正方形地板砖的边长为,是的中点,则图案中小正方形的边长为( )
A.
B.
C.
D.
8.数据分析是从数据中获取有效信息的重要手段请根据如下某组数据的方差计算式:你不能得到的有效信息是( )
A. 这组数据的中位数是 B. 这组数据的平均数是
C. 这组数据的众数是 D. 这组数据的方差是
9.如图,在中,,点从点出发沿边向点运动,运动到点停止,过点分别作交于点,交于点,则四边形形状的变化依次为( )
A. 矩形菱形矩形 B. 矩形正方形矩形
C. 平行四边形菱形平行四边形 D. 平行四边形正方形平行四边形
10.如图,直线分别与轴、轴交于,两点,以为边作正方形,双曲线经过点,则的值为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.计算:______.
12.将直线向上平移个单位长度后,得到的新直线的解析式是______.
13.某校规定学生的数学成绩由三部分组成,平时成绩占,期中考试成绩占,期末考试成绩占,若小晓同学的三项成绩分别是分,分,分,则小晓同学本学期的数学成绩应记为______分
14.如图,在平面直角坐标系中,过点分别作轴于点,轴于点,反比例函数的图象分别与,相交于,两点,连接,若四边形的面积为,则的值为______.
15.方胜纹是中国传统纹样,寓意吉祥如图是一个刻有方胜纹的方胜盘,图是方胜盘的示意图,菱形与菱形是完全相同的两个菱形,中间四边形也是菱形,若,,,为的中点,则四边形的面积为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
化简:.
17.本小题分
中华优秀传统文化源远流长、是中华文明的智慧结晶孙子算经周髀算经是我国古代较为普及的算书,书中许多问题浅显有趣某书店的孙子算经单价是周髀算经单价的,用元购买孙子算经比购买周髀算经多买本求两种图书的单价分别为多少元.
18.本小题分
如图,已知四边形中,,,求证:四边形是平行四边形.
19.本小题分
某中学八年级甲、乙两班分别选名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示.
根据图中数据填写如表:
平均数 中位数 众数 方差
甲班 ______ ______
乙班 ______
根据上表数据你认为哪班的成绩较好?请说明你的理由.
20.本小题分
如图,直线与双曲线相交于点,.
求双曲线及直线对应的函数表达式;
将直线向下平移至处,其中点,点在轴上连接,,求的面积;
请直接写出关于的不等式的解集.
21.本小题分
如图,在中,点是的中点,以、为边作平行四边形,连接、,回答以下问题.
求证:四边形是平行四边形;
如果,求证:四边形是矩形.
22.本小题分
如图,在平面直角坐标系中,菱形的顶点与原点重合,点在轴的正半轴上,点在反比例函数的图象上,点的坐标为.
求的值;
若将菱形沿轴正方向平移,当菱形的顶点落在函数的图象上时,求菱形沿轴正方向平移的距离.
23.本小题分
如图,在菱形中,,,点是边的中点点是边上的一个动点不与点重合,延长交的延长线于点,连接,.
求证:四边形是平行四边形.
问当的长度是多少时,四边形是矩形;
问当的长度是多少时,四边形是菱形.
答案和解析
1.
解:最简公分母是,原方程有增根,
最简公分母,
增根是.
故选:.
2.
解:,
故选:.
3.
解:由题意得,,
,
,
关于的函数解析式是,
故选:.
4.
解:这组数据,,,,的平均数是:
根据,,,,的平均数是,
,
,
把代入得:
,
.
故选:.
5.
解:与直线关于轴对称的点的坐标为横坐标互为相反数,纵坐标不变,则,即.
经过点,
,
,
故选:.
6.
解:四边形是平行四边形,
,,
,,
在平行四边形中,::,
,
,
,
,
故选:.
7.
解:设,、、为大正方形的三个顶点,、为五边形的顶点,则,
大正方形由四个全等的五边形和一个小正方形组成,大正方形的边长为,
,,,,
四边形是矩形,
,,
,,且,
,
,
,
是的中点,
,
,
解得,
小正方形的边长为,
故选:.
8.
解:根据方差公式可得这一组数据为,,,,,
A、这组数据的中位数是,原选项不符合题意;
B、这组数据的平均数是,原选项不符合题意;
C、由于出现次数最多,则这组数据的众数是,原选项不符合题意;
D、这组数据的平均数是,
,
原选项符合题意;
故选:.
9.
解:,,
四边形是平行四边形,
,
平行四边形是矩形,
在点的运动过程中,四边形始终是矩形,
当时,矩形是正方形,
四边形形状的变化依次为:矩形正方形矩形.
故选:.
10.
解:对于,当时,,当时,,
点,点,
,,
过点作于点,如下图所示:
,,
四边形为正方形,
,,
,
,
在和中,
,
≌,
,,
,
点的坐标为,
双曲线经过点,
.
故选:.
11.
解:原式.
故答案为:.
12.
解:将直线向上平移个单位长度,得到的新直线的解析式为:.
故答案为:.
13.
解:小晓同学本学期的数学成绩应记为分,
故答案为:.
14.
解:点,作轴于点,轴于点,
,
点、在反比例函数图象上,
.
反比例函数图象在第二象限,
.
故答案为:.
15.
解:在菱形中,,,
,
,
为的中点,
,
菱形的面积,
故答案为:.
16.;
.
原式
;
原式
.
17.解:设周髀算经单价为元,则孙子算经单价为元.
依题意得,
解得.
经检验,是原方程的解,且符合题意,
元.
答:周髀算经单价为元,孙子算经单价为元.
18.证明:,,,
,
又,
,
,,
四边形是平行四边形两组对边分别平行的四边形是平行四边形.
19.,,;
答案不唯一,只要言之有理即可,具体见解答.
解:甲班个数据中出现了次,是出现次数最多的数据,
甲班成绩的众数为:;
甲班成绩的方差为:;
乙班成绩由小到大排列为:,,,,,处在中间的数据是,
乙班成绩的中位数为:,
故答案为:,,;
答案不唯一,只要言之有理即可,比如:
从平均数看,两班成绩的平均线相同,则甲、乙成绩一样好;
从中位数看,甲班成绩的中位数高,故甲班的成绩好;
从方差看,甲班的方差小,成绩稳定,故甲班的成绩好.
20.解:将代入双曲线,
,
双曲线的解析式为,
将点代入,
,
,
将,代入,
,
解得,
直线解析式为;
直线向下平移至,
,
设直线的解析式为,
将点代入,
,
解得,
直线的解析式为,
,
过点作交于,
设直线与轴的交点为,与轴的交点为,
,,
,,
,
,,
,
,
,
,
,
,
的面积;
由图可知时,.
21.见解析过程;
见解析过程.
证明:四边形是平行四边形,
,,
点是的中点,
,
,
且,
四边形是平行四边形;
,点是的中点,
,
四边形是矩形.
22.解:过点作轴的垂线,垂足为,
点的坐标为,
,,
,
,
点坐标为,
,
;
将菱形沿轴正方向平移,使得点落在函数的图象点处,
过点做轴的垂线,垂足为.
,
,
点的纵坐标为,
点在的图象上
,
解得:,
即,
,
菱形平移的距离为.
23.证明:四边形是菱形,
,
,,
又点是边的中点
,
≌,
,
四边形是平行四边形;
解:当的值为时,四边形是矩形.
理由如下:
,
点是边的中点,
,
,
是等边三角形,
,,
,
,即,
平行四边形是矩形.
故答案为:
当的值为时,四边形是菱形.
理由如下:
,
,
,
是等边三角形,
,
平行四边形是菱形.
同课章节目录
