贵州省2025届中考数学真题(含答案)
图片预览


文档简介
贵州省2025届中考数学试卷
一、单选题
1.如果向前运动记作,那么向后运动,记作( )
A. B. C. D.
2.下列图中能说明一定成立的是( )
A. B. C. D.
3.贵州省的“花江峡谷大桥”因跨越花江大峡谷而得名,其中主桥跨径1420m,桥面至水面高度625m.建成后,会成为新的世界第一高桥和世界第一的山区跨径桥梁.1420这个数用科学记数法可表示为( )
A. B. C. D.
4.如图,小红想将一张矩形纸片沿剪下后得到一个,若,则的度数是( )
A. B. C. D.
5.如图,在平面直角坐标系中有A,B,C,D四点,根据图中各点位置判断,哪一个点在第四象限( )
A.点 B.点 C.点 D.点
6.已知是关于的方程的解,则的值为( )
A.3 B.4 C.5 D.6
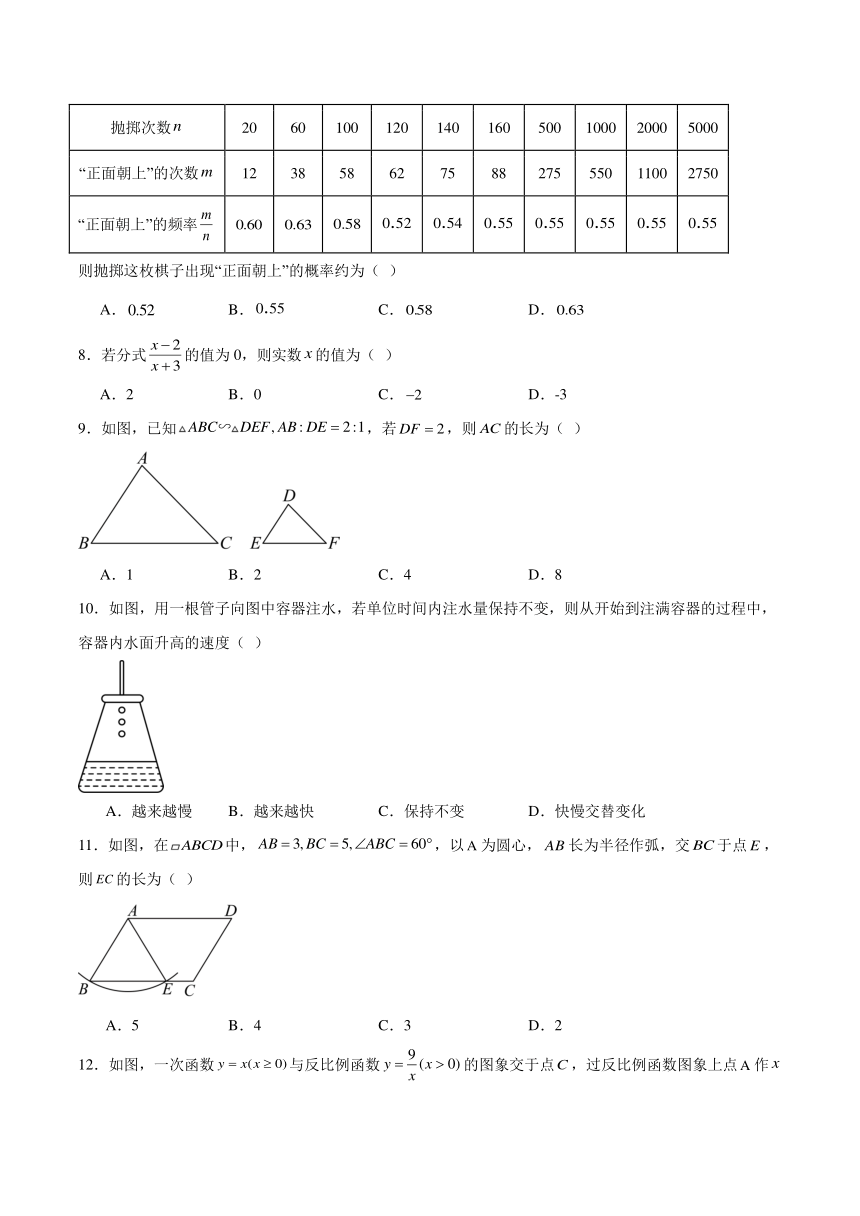
7.某学习小组抛掷一枚质地不均匀的棋子,为了估计“正面朝上”的概率,将同学们获得的试验数据整理如下表:( )
抛掷次数 20 60 100 120 140 160 500 1000 2000 5000
“正面朝上”的次数 12 38 58 62 75 88 275 550 1100 2750
“正面朝上”的频率
则抛掷这枚棋子出现“正面朝上”的概率约为( )
A. B. C. D.
8.若分式的值为0,则实数的值为( )
A.2 B.0 C. D.-3
9.如图,已知,若,则的长为( )
A.1 B.2 C.4 D.8
10.如图,用一根管子向图中容器注水,若单位时间内注水量保持不变,则从开始到注满容器的过程中,容器内水面升高的速度( )
A.越来越慢 B.越来越快 C.保持不变 D.快慢交替变化
11.如图,在中,,以为圆心,长为半径作弧,交于点,则的长为( )
A.5 B.4 C.3 D.2
12.如图,一次函数与反比例函数的图象交于点,过反比例函数图象上点作轴垂线,垂足为点,交的图象于点,点的横坐标为1.有以下结论:
①线段AB的长为8;
②点的坐标为;
③当时,一次函数的值小于反比例函数的值.
其中结论正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题
13.一个不透明的袋子中装有2个红球和3个黄球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是 .
14.实数a,b在数轴上的对应点的位置如图所示,则与的大小关系是 b.(填“”“”或“”)
15.一元二次方程 的根是 .
16.如图,在矩形中,点E,F,M分别在,,边上,分别交对角线、线段于点G,H,且是的中点.若,则的长为 .
三、解答题
17.(1)计算:;
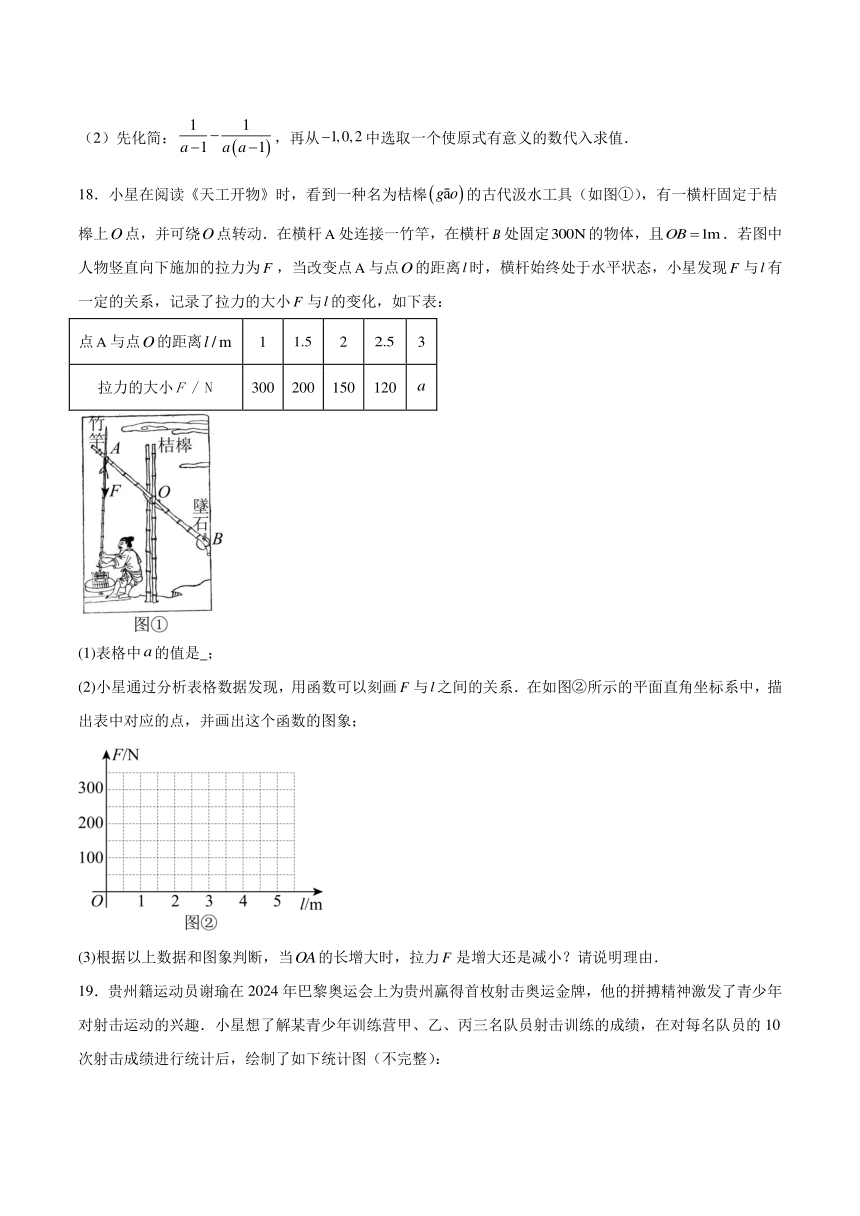
(2)先化简:,再从中选取一个使原式有意义的数代入求值.
18.小星在阅读《天工开物》时,看到一种名为桔槔的古代汲水工具(如图①),有一横杆固定于桔槔上点,并可绕点转动.在横杆处连接一竹竿,在横杆处固定的物体,且.若图中人物竖直向下施加的拉力为,当改变点与点的距离时,横杆始终处于水平状态,小星发现与有一定的关系,记录了拉力的大小与的变化,如下表:
点与点的距离 1 2 3
拉力的大小 300 200 150 120
(1)表格中的值是 ;
(2)小星通过分析表格数据发现,用函数可以刻画与之间的关系.在如图②所示的平面直角坐标系中,描出表中对应的点,并画出这个函数的图象;
(3)根据以上数据和图象判断,当的长增大时,拉力是增大还是减小?请说明理由.
19.贵州籍运动员谢瑜在2024年巴黎奥运会上为贵州赢得首枚射击奥运金牌,他的拼搏精神激发了青少年对射击运动的兴趣.小星想了解某青少年训练营甲、乙、丙三名队员射击训练的成绩,在对每名队员的10次射击成绩进行统计后,绘制了如下统计图(不完整):
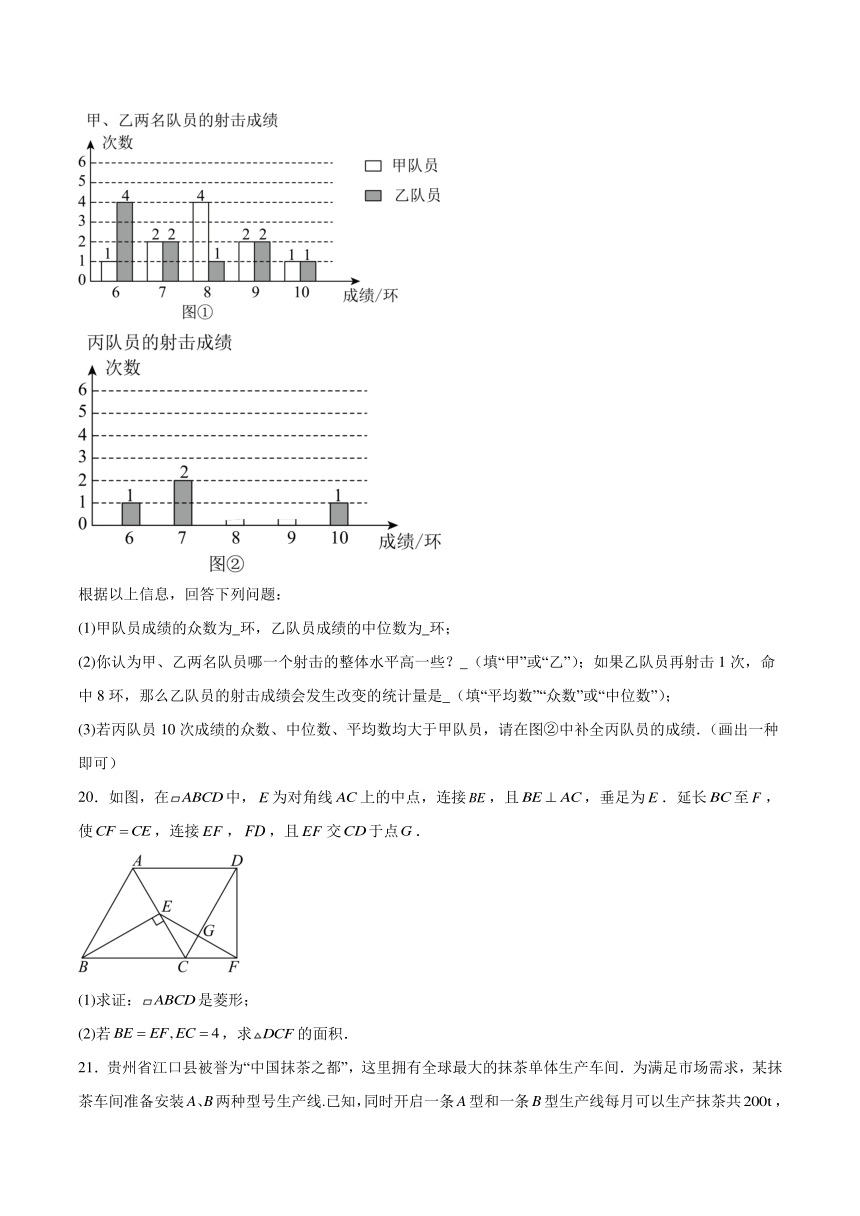
根据以上信息,回答下列问题:
(1)甲队员成绩的众数为 环,乙队员成绩的中位数为 环;
(2)你认为甲、乙两名队员哪一个射击的整体水平高一些? (填“甲”或“乙”);如果乙队员再射击1次,命中8环,那么乙队员的射击成绩会发生改变的统计量是 (填“平均数”“众数”或“中位数”);
(3)若丙队员10次成绩的众数、中位数、平均数均大于甲队员,请在图②中补全丙队员的成绩.(画出一种即可)
20.如图,在中,为对角线上的中点,连接,且,垂足为.延长至,使,连接,,且交于点.
(1)求证:是菱形;
(2)若,求的面积.
21.贵州省江口县被誉为“中国抹茶之都”,这里拥有全球最大的抹茶单体生产车间.为满足市场需求,某抹茶车间准备安装A、B两种型号生产线.已知,同时开启一条A型和一条B型生产线每月可以生产抹茶共,同时开启一条A型和两条B型生产线每月可以生产抹茶共.
(1)求一条A型和一条B型生产线每月各生产抹茶多少吨?
(2)为扩大生产规模,若另一车间准备同时安装相同型号的A、B两种生产线共5条,该车间接到一个订单,要求4个月生产抹茶不少于,至少需要安装多少条A型生产线?
22.某小区在设计时,计划在如图①的住宅楼正前方建一栋文体活动中心.设计示意图如图②所示,已知,该地冬至正午太阳高度角为.如果你是建筑设计师,请结合示意图和已知条件完成下列任务.
任务一:计算冬至正午太阳照到住宅楼的位置与地面之间的距离的长;
任务二:为符合建筑规范对日照的要求,让整栋住宅楼在冬至正午太阳高度角下恰好都能照射到阳光,需将活动中心沿方向移动一定的距离(活动中心高度不变),求该活动中心移动了多少米?
(参考数据:.结果保留小数点后一位)
23.如图,在中,是直角,为的中点,为的切线交的延长线于点.连接,.
(1)点与的位置关系是 ,线段与线段的数量关系是 ;
(2)过点作,与的延长线交于点.根据题意补全图形,判断的形状,并说明理由;
(3)在(2)的条件下,若的半径为,求的长.
24.用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点,运动路径近似为抛物线,且,石块在水面上弹起后第二次与水面接触于点,运动路径近似为抛物线,且.(小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
(1)如图②,当时,若点坐标为,求抛物线的表达式;
(2)在(1)的条件下,若,在水面上有一个截面宽,高的矩形的障碍物,点的坐标为,判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;
(3)小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中,求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)
25.如图,在菱形中,,点为线段上一动点,点为射线上的一点(点与点不重合).
【问题解决】
(1)如图①,若点与线段的中点重合,则 度,线段与线段的位置关系是 ;
【问题探究】
(2)如图②,在点运动过程中,点在线段上,且,探究线段与线段的数量关系,并说明理由;
【拓展延伸】
(3)在点运动过程中,将线段绕点逆时针旋转得到,射线交射线于点,若,求的长.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C B D C B A C B
题号 11 12
答案 D C
13./
14.
15.,
16.
17.(1);(2),当时,原式;当时,原式.
解:(1)
;
(2)
,
∵分式要有意义,
∴,
∴且,
∴当时,原式;当时,原式.
18.(1)100
(2)见解析
(3)当的长增大时,拉力减小,理由见解析
(1)解:根据表格中的数据发现:
,
因此点与点的距离与拉力F的乘积不变,
∴;
(2)解:与之间的函数图象,如图所示:
(3)解:由函数图象可知:F是l的反比例函数,且该函数图象在第一象限内,根据反比例函数的性质可知,F随l的增大而减小,所以当的长增大时,拉力减小.
19.(1),
(2)甲;平均数
(3)见解析
(1)解:甲队员的射击成绩为:、、、、、、、、、,故甲队员成绩的众数为环;
乙队员的射击成绩为:、、、、、、、、、,乙队员成绩的中位数为环;
(2)解:,
,
,
,
故,,
∴甲队员射击的整体水平高一些,
如果乙队员再射击1次,命中8环,那么乙队员的射击成绩为、、、、、、、、、、,
此时平均数为,众数为,中位数为,
故会发生改变的统计量是平均数;
(3)解:甲队员的射击成绩为:、、、、、、、、、,故甲队员成绩的中位数为环,甲队员成绩的众数为环,
由(2)可得,
∵丙队员10次成绩的众数、中位数、平均数均大于甲队员,
∴补全丙队员的成绩如下:
此时丙队员10次成绩的众数为、中位数为、平均数均,均大于甲队员.
20.(1)见解析
(2)
(1)证明:∵为对角线上的中点,且,
∴垂直平分,
∴,
∵四边形是平行四边形,
∴是菱形;
(2)解:如图:
∵,
∴,
设
∴,
∵,
∴,
∴,
解得:
∴,
∵,
∴,
∵,
∴为等边三角形,
∴
∵四边形是菱形,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
21.(1)一条A型生产线每月生产抹茶,一条B型生产线每月生产抹茶
(2)至少需要安装3条A型生产线
(1)解:设一条A型生产线每月生产抹茶,一条B型生产线每月生产抹茶,
由题意得:,
解得:,
答:一条A型生产线每月生产抹茶,一条B型生产线每月生产抹茶;
(2)解:设需要安装条A型生产线,则安装B种生产线条,
由题意得:,
解得:,
∵为正整数,
∴最小取,
答:至少需要安装3条A型生产线.
22.任务一:,任务二:该活动中心移动了2米;
解:任务一:如图,过作于,
结合题意可得:四边形为矩形,,
∵,
∴,,
∵,
∴,
∴;
任务二:如图,过作的平行线,过作的平行线,两线交于点,交于点,过作于,
∴,四边形为矩形,
∴,
∴,
∴;
∴该活动中心移动了2米.
23.(1)在线段上;;
(2)补图见解析,为等腰三角形
(3)
(1)解:∵是直角,
∴为直径,
∵为圆心,
∴在线段上;
∵为的中点,
∴,
∴;
(2)解:补图如下,为等腰三角形,理由如下:
连接,
∵为的切线交的延长线于点,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴是等腰三角形;
(3)解:如图,过作于,
∵的半径为,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
24.(1)
(2)不能,理由见解析
(3)
(1)∵当时,
∵点坐标为
∴
∴
∴抛物线的表达式为;
(2)不能,理由如下:
∵,点坐标为
∴
∴
∵点的坐标为,
∴
∴将代入
∴此时石块沿抛物线运动时不能越过障碍物;
(3)∵正方形,
∴
∴如图所示,
∵抛物线开口向下
∴
∵越小开口越大,越大开口越小,点在和之间(包括这两点)
∴由图象可得,当抛物线顶点为点M,且经过点时,开口最大,此时a最大
∴设的表达式为
将代入得,
解得;
∴由图象可得,当抛物线顶点为点P,且经过点时,开口最小,此时a最小
∴设的表达式为
将代入得,
解得;
∴的取值范围为.
25.(1),;(2),理由见解析;(3)的长为或.
解:(1)∵在菱形中,
∴,
∵,
∴为等边三角形,
∵点与线段的中点重合,
∴,;
(2)如图,把绕顺时针旋转得到,
∴,,,
∴为等边三角形,
∴,,
∵点在线段上,且,
∴,,
∴,,
∴,
∴,
∴;
(3)如图,当在线段上,记与交于点,
∵,
∴,
∵,
∴,
∴,
∴,
设,则,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵为等边三角形,
∴,
∴,
如图,当在线段上时,延长交于,
同理可得:,,
∴,
设,而,则,
∴,
∴,
同理:,
∴,
∴,
综上:的长为或.
一、单选题
1.如果向前运动记作,那么向后运动,记作( )
A. B. C. D.
2.下列图中能说明一定成立的是( )
A. B. C. D.
3.贵州省的“花江峡谷大桥”因跨越花江大峡谷而得名,其中主桥跨径1420m,桥面至水面高度625m.建成后,会成为新的世界第一高桥和世界第一的山区跨径桥梁.1420这个数用科学记数法可表示为( )
A. B. C. D.
4.如图,小红想将一张矩形纸片沿剪下后得到一个,若,则的度数是( )
A. B. C. D.
5.如图,在平面直角坐标系中有A,B,C,D四点,根据图中各点位置判断,哪一个点在第四象限( )
A.点 B.点 C.点 D.点
6.已知是关于的方程的解,则的值为( )
A.3 B.4 C.5 D.6
7.某学习小组抛掷一枚质地不均匀的棋子,为了估计“正面朝上”的概率,将同学们获得的试验数据整理如下表:( )
抛掷次数 20 60 100 120 140 160 500 1000 2000 5000
“正面朝上”的次数 12 38 58 62 75 88 275 550 1100 2750
“正面朝上”的频率
则抛掷这枚棋子出现“正面朝上”的概率约为( )
A. B. C. D.
8.若分式的值为0,则实数的值为( )
A.2 B.0 C. D.-3
9.如图,已知,若,则的长为( )
A.1 B.2 C.4 D.8
10.如图,用一根管子向图中容器注水,若单位时间内注水量保持不变,则从开始到注满容器的过程中,容器内水面升高的速度( )
A.越来越慢 B.越来越快 C.保持不变 D.快慢交替变化
11.如图,在中,,以为圆心,长为半径作弧,交于点,则的长为( )
A.5 B.4 C.3 D.2
12.如图,一次函数与反比例函数的图象交于点,过反比例函数图象上点作轴垂线,垂足为点,交的图象于点,点的横坐标为1.有以下结论:
①线段AB的长为8;
②点的坐标为;
③当时,一次函数的值小于反比例函数的值.
其中结论正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题
13.一个不透明的袋子中装有2个红球和3个黄球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是 .
14.实数a,b在数轴上的对应点的位置如图所示,则与的大小关系是 b.(填“”“”或“”)
15.一元二次方程 的根是 .
16.如图,在矩形中,点E,F,M分别在,,边上,分别交对角线、线段于点G,H,且是的中点.若,则的长为 .
三、解答题
17.(1)计算:;
(2)先化简:,再从中选取一个使原式有意义的数代入求值.
18.小星在阅读《天工开物》时,看到一种名为桔槔的古代汲水工具(如图①),有一横杆固定于桔槔上点,并可绕点转动.在横杆处连接一竹竿,在横杆处固定的物体,且.若图中人物竖直向下施加的拉力为,当改变点与点的距离时,横杆始终处于水平状态,小星发现与有一定的关系,记录了拉力的大小与的变化,如下表:
点与点的距离 1 2 3
拉力的大小 300 200 150 120
(1)表格中的值是 ;
(2)小星通过分析表格数据发现,用函数可以刻画与之间的关系.在如图②所示的平面直角坐标系中,描出表中对应的点,并画出这个函数的图象;
(3)根据以上数据和图象判断,当的长增大时,拉力是增大还是减小?请说明理由.
19.贵州籍运动员谢瑜在2024年巴黎奥运会上为贵州赢得首枚射击奥运金牌,他的拼搏精神激发了青少年对射击运动的兴趣.小星想了解某青少年训练营甲、乙、丙三名队员射击训练的成绩,在对每名队员的10次射击成绩进行统计后,绘制了如下统计图(不完整):
根据以上信息,回答下列问题:
(1)甲队员成绩的众数为 环,乙队员成绩的中位数为 环;
(2)你认为甲、乙两名队员哪一个射击的整体水平高一些? (填“甲”或“乙”);如果乙队员再射击1次,命中8环,那么乙队员的射击成绩会发生改变的统计量是 (填“平均数”“众数”或“中位数”);
(3)若丙队员10次成绩的众数、中位数、平均数均大于甲队员,请在图②中补全丙队员的成绩.(画出一种即可)
20.如图,在中,为对角线上的中点,连接,且,垂足为.延长至,使,连接,,且交于点.
(1)求证:是菱形;
(2)若,求的面积.
21.贵州省江口县被誉为“中国抹茶之都”,这里拥有全球最大的抹茶单体生产车间.为满足市场需求,某抹茶车间准备安装A、B两种型号生产线.已知,同时开启一条A型和一条B型生产线每月可以生产抹茶共,同时开启一条A型和两条B型生产线每月可以生产抹茶共.
(1)求一条A型和一条B型生产线每月各生产抹茶多少吨?
(2)为扩大生产规模,若另一车间准备同时安装相同型号的A、B两种生产线共5条,该车间接到一个订单,要求4个月生产抹茶不少于,至少需要安装多少条A型生产线?
22.某小区在设计时,计划在如图①的住宅楼正前方建一栋文体活动中心.设计示意图如图②所示,已知,该地冬至正午太阳高度角为.如果你是建筑设计师,请结合示意图和已知条件完成下列任务.
任务一:计算冬至正午太阳照到住宅楼的位置与地面之间的距离的长;
任务二:为符合建筑规范对日照的要求,让整栋住宅楼在冬至正午太阳高度角下恰好都能照射到阳光,需将活动中心沿方向移动一定的距离(活动中心高度不变),求该活动中心移动了多少米?
(参考数据:.结果保留小数点后一位)
23.如图,在中,是直角,为的中点,为的切线交的延长线于点.连接,.
(1)点与的位置关系是 ,线段与线段的数量关系是 ;
(2)过点作,与的延长线交于点.根据题意补全图形,判断的形状,并说明理由;
(3)在(2)的条件下,若的半径为,求的长.
24.用石块打水漂是一项有趣的活动.抛掷后的石块与平静的水面接触.石块会在空中近似的形成一组抛物线的运动路径.如图①,小星站在河边的安全位置用一个石块打水漂,石块在空中飞行的高度y与水平距离之间的关系如图②所示.石块第一次与水面接触于点,运动路径近似为抛物线,且,石块在水面上弹起后第二次与水面接触于点,运动路径近似为抛物线,且.(小星所在地面、水面在同一平面内,且石块形状大小、空气阻力等因素忽略不计)
(1)如图②,当时,若点坐标为,求抛物线的表达式;
(2)在(1)的条件下,若,在水面上有一个截面宽,高的矩形的障碍物,点的坐标为,判断此时石块沿抛物线运动时是否能越过障碍物?请说明理由;
(3)小星在抛掷石块时,若的顶点需在一个正方形区域内(包括边界),且点在和之间(包括这两点),其中,求的取值范围.(在抛掷过程中正方形与拋物线在同一平面内)
25.如图,在菱形中,,点为线段上一动点,点为射线上的一点(点与点不重合).
【问题解决】
(1)如图①,若点与线段的中点重合,则 度,线段与线段的位置关系是 ;
【问题探究】
(2)如图②,在点运动过程中,点在线段上,且,探究线段与线段的数量关系,并说明理由;
【拓展延伸】
(3)在点运动过程中,将线段绕点逆时针旋转得到,射线交射线于点,若,求的长.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C B D C B A C B
题号 11 12
答案 D C
13./
14.
15.,
16.
17.(1);(2),当时,原式;当时,原式.
解:(1)
;
(2)
,
∵分式要有意义,
∴,
∴且,
∴当时,原式;当时,原式.
18.(1)100
(2)见解析
(3)当的长增大时,拉力减小,理由见解析
(1)解:根据表格中的数据发现:
,
因此点与点的距离与拉力F的乘积不变,
∴;
(2)解:与之间的函数图象,如图所示:
(3)解:由函数图象可知:F是l的反比例函数,且该函数图象在第一象限内,根据反比例函数的性质可知,F随l的增大而减小,所以当的长增大时,拉力减小.
19.(1),
(2)甲;平均数
(3)见解析
(1)解:甲队员的射击成绩为:、、、、、、、、、,故甲队员成绩的众数为环;
乙队员的射击成绩为:、、、、、、、、、,乙队员成绩的中位数为环;
(2)解:,
,
,
,
故,,
∴甲队员射击的整体水平高一些,
如果乙队员再射击1次,命中8环,那么乙队员的射击成绩为、、、、、、、、、、,
此时平均数为,众数为,中位数为,
故会发生改变的统计量是平均数;
(3)解:甲队员的射击成绩为:、、、、、、、、、,故甲队员成绩的中位数为环,甲队员成绩的众数为环,
由(2)可得,
∵丙队员10次成绩的众数、中位数、平均数均大于甲队员,
∴补全丙队员的成绩如下:
此时丙队员10次成绩的众数为、中位数为、平均数均,均大于甲队员.
20.(1)见解析
(2)
(1)证明:∵为对角线上的中点,且,
∴垂直平分,
∴,
∵四边形是平行四边形,
∴是菱形;
(2)解:如图:
∵,
∴,
设
∴,
∵,
∴,
∴,
解得:
∴,
∵,
∴,
∵,
∴为等边三角形,
∴
∵四边形是菱形,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
21.(1)一条A型生产线每月生产抹茶,一条B型生产线每月生产抹茶
(2)至少需要安装3条A型生产线
(1)解:设一条A型生产线每月生产抹茶,一条B型生产线每月生产抹茶,
由题意得:,
解得:,
答:一条A型生产线每月生产抹茶,一条B型生产线每月生产抹茶;
(2)解:设需要安装条A型生产线,则安装B种生产线条,
由题意得:,
解得:,
∵为正整数,
∴最小取,
答:至少需要安装3条A型生产线.
22.任务一:,任务二:该活动中心移动了2米;
解:任务一:如图,过作于,
结合题意可得:四边形为矩形,,
∵,
∴,,
∵,
∴,
∴;
任务二:如图,过作的平行线,过作的平行线,两线交于点,交于点,过作于,
∴,四边形为矩形,
∴,
∴,
∴;
∴该活动中心移动了2米.
23.(1)在线段上;;
(2)补图见解析,为等腰三角形
(3)
(1)解:∵是直角,
∴为直径,
∵为圆心,
∴在线段上;
∵为的中点,
∴,
∴;
(2)解:补图如下,为等腰三角形,理由如下:
连接,
∵为的切线交的延长线于点,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴是等腰三角形;
(3)解:如图,过作于,
∵的半径为,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
24.(1)
(2)不能,理由见解析
(3)
(1)∵当时,
∵点坐标为
∴
∴
∴抛物线的表达式为;
(2)不能,理由如下:
∵,点坐标为
∴
∴
∵点的坐标为,
∴
∴将代入
∴此时石块沿抛物线运动时不能越过障碍物;
(3)∵正方形,
∴
∴如图所示,
∵抛物线开口向下
∴
∵越小开口越大,越大开口越小,点在和之间(包括这两点)
∴由图象可得,当抛物线顶点为点M,且经过点时,开口最大,此时a最大
∴设的表达式为
将代入得,
解得;
∴由图象可得,当抛物线顶点为点P,且经过点时,开口最小,此时a最小
∴设的表达式为
将代入得,
解得;
∴的取值范围为.
25.(1),;(2),理由见解析;(3)的长为或.
解:(1)∵在菱形中,
∴,
∵,
∴为等边三角形,
∵点与线段的中点重合,
∴,;
(2)如图,把绕顺时针旋转得到,
∴,,,
∴为等边三角形,
∴,,
∵点在线段上,且,
∴,,
∴,,
∴,
∴,
∴;
(3)如图,当在线段上,记与交于点,
∵,
∴,
∵,
∴,
∴,
∴,
设,则,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵为等边三角形,
∴,
∴,
如图,当在线段上时,延长交于,
同理可得:,,
∴,
设,而,则,
∴,
∴,
同理:,
∴,
∴,
综上:的长为或.
同课章节目录
