河南省商丘市2024-2025学年八年级下学期6月期末考试数学试卷(含解析)
文档属性
| 名称 | 河南省商丘市2024-2025学年八年级下学期6月期末考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 14:19:30 | ||
图片预览


文档简介
河南省商丘市2024-2025学年八年级下学期6月期末数学试卷
一、单选题
1.下列各式一定是二次根式的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列关系式中:①;②;③;④;⑤;⑥,其中y是x的函数的有( )
A.3个 B.4个 C.5个 D.6个
4.如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间 B.3和4之间 C.-5和-4之间 D.4和5之间
5.河南省曲剧团中六位曲剧演员的年龄(单位:岁)分别为26,24,29,31,28,29,则四年后这六位曲剧演员的年龄数据中一定不会改变的是( )
A.众数 B.方差 C.平均数 D.中位数
6.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A., B.,
C., D.,
7.已知点,点是上的两点,则与的大小关系是( )
A. B. C. D.
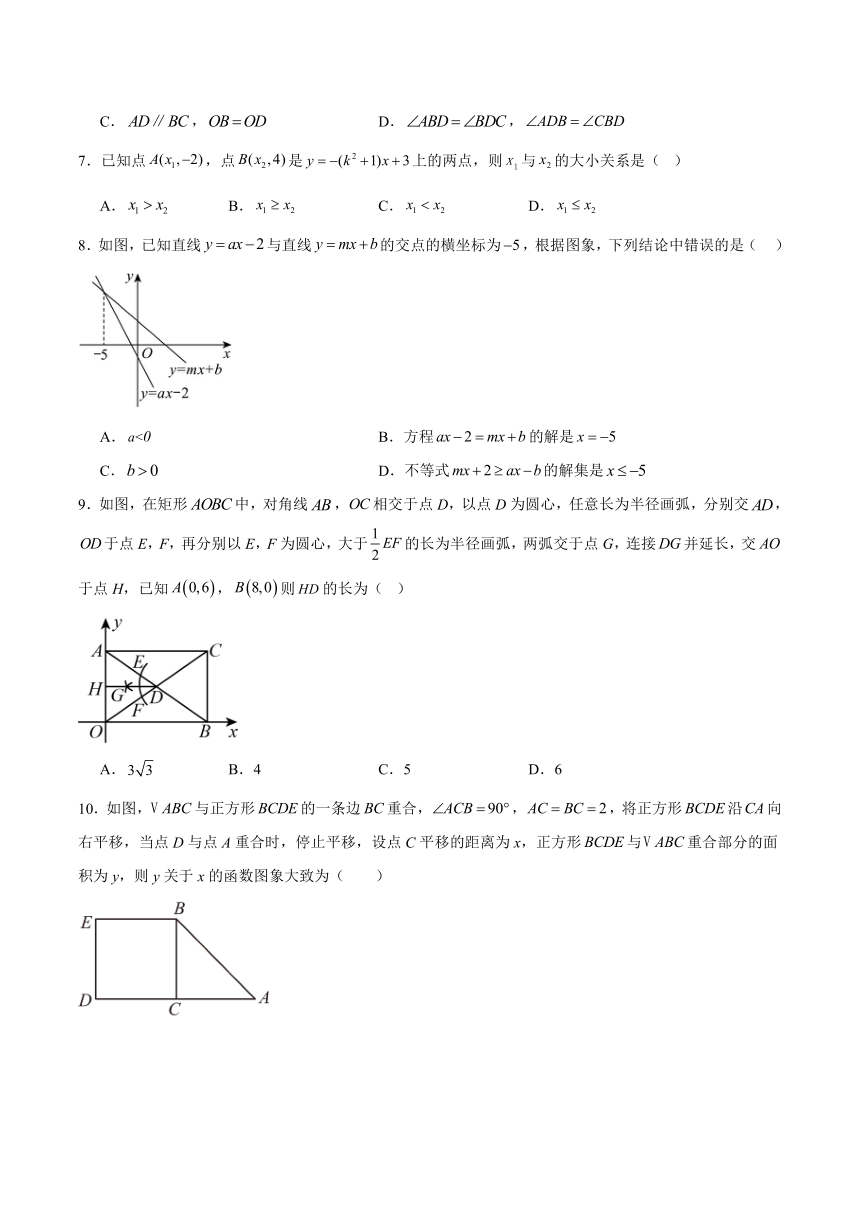
8.如图,已知直线与直线的交点的横坐标为,根据图象,下列结论中错误的是( )
A. B.方程的解是
C. D.不等式的解集是
9.如图,在矩形中,对角线,相交于点D,以点D为圆心,任意长为半径画弧,分别交,于点E,F,再分别以E,F为圆心,大于的长为半径画弧,两弧交于点G,连接并延长,交于点H,已知,则的长为( )
A. B.4 C.5 D.6
10.如图,与正方形的一条边重合,,,将正方形沿向右平移,当点D与点A重合时,停止平移,设点C平移的距离为x,正方形与重合部分的面积为y,则y关于x的函数图象大致为( )
A. B. C. D.
二、填空题
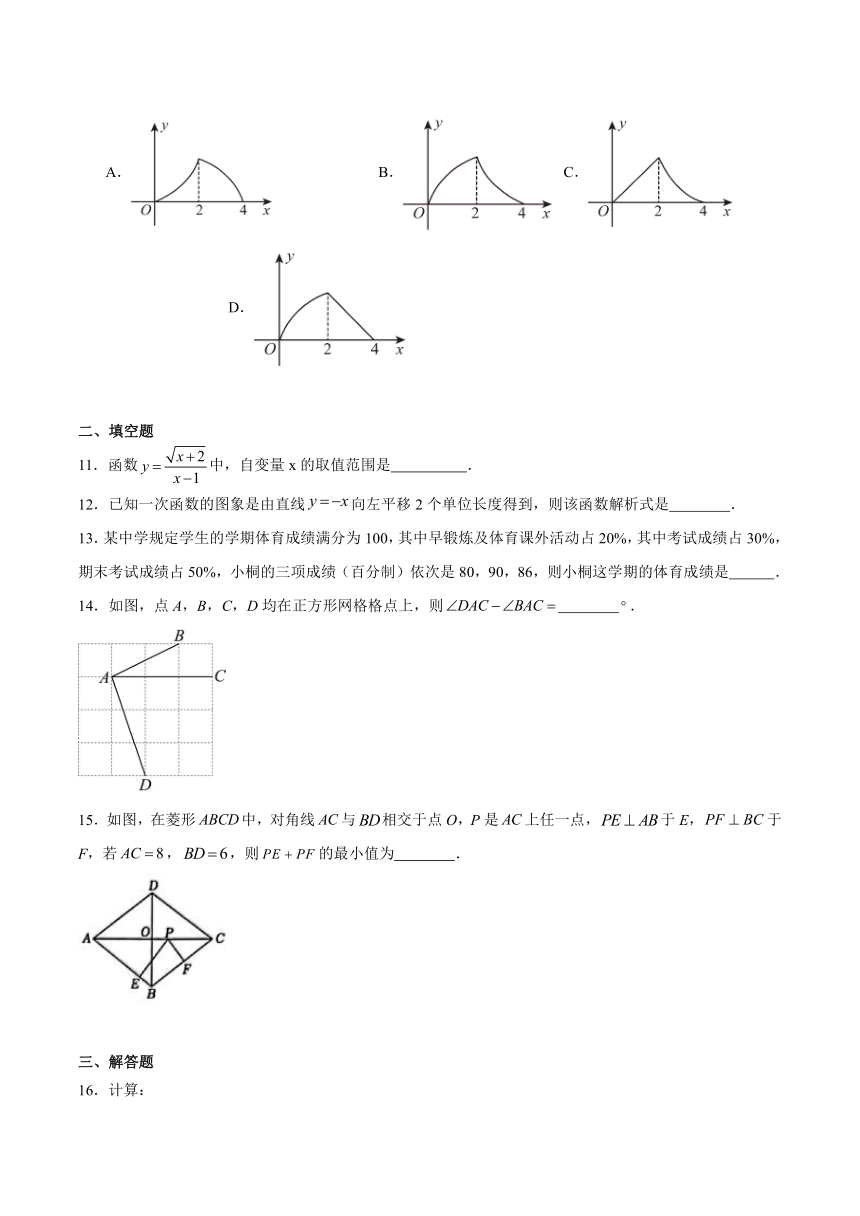
11.函数中,自变量x的取值范围是 .
12.已知一次函数的图象是由直线向左平移2个单位长度得到,则该函数解析式是 .
13.某中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占20%,其中考试成绩占30%,期末考试成绩占50%,小桐的三项成绩(百分制)依次是80,90,86,则小桐这学期的体育成绩是 .
14.如图,点A,B,C,D均在正方形网格格点上,则 .
15.如图,在菱形中,对角线与相交于点O,P是上任一点,于E,于F,若,,则的最小值为 .
三、解答题
16.计算:
(1)
(2)
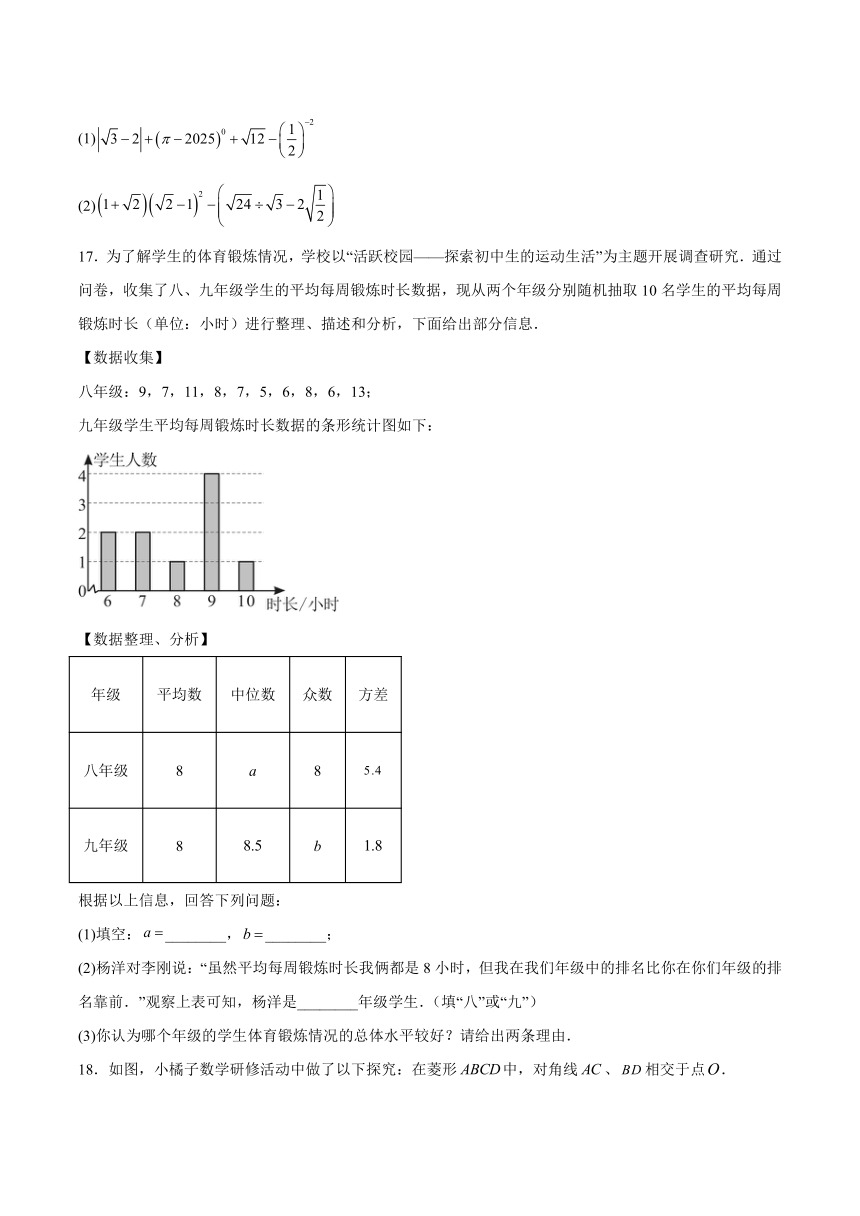
17.为了解学生的体育锻炼情况,学校以“活跃校园——探索初中生的运动生活”为主题开展调查研究.通过问卷,收集了八、九年级学生的平均每周锻炼时长数据,现从两个年级分别随机抽取10名学生的平均每周锻炼时长(单位:小时)进行整理、描述和分析,下面给出部分信息.
【数据收集】
八年级:9,7,11,8,7,5,6,8,6,13;
九年级学生平均每周锻炼时长数据的条形统计图如下:
【数据整理、分析】
年级 平均数 中位数 众数 方差
八年级 8 a 8
九年级 8 b
根据以上信息,回答下列问题:
(1)填空:________,________;
(2)杨洋对李刚说:“虽然平均每周锻炼时长我俩都是8小时,但我在我们年级中的排名比你在你们年级的排名靠前.”观察上表可知,杨洋是________年级学生.(填“八”或“九”)
(3)你认为哪个年级的学生体育锻炼情况的总体水平较好?请给出两条理由.
18.如图,小橘子数学研修活动中做了以下探究:在菱形中,对角线、相交于点.
(1)尺规作图:在的延长线上截取,连接,再过点 作的垂线交于点 (保留作图痕迹,不写作法);
(2)求证: 四边形为矩形.
19.研究新函数,可以通过一次函数的图象和性质的学习过程来探究新函数.
(1)补全下表:
x … 0 1 2 3 …
y … ________ 1 ________
(2)根据(1)中的数据在下图中画出函数图象;
(3)根据(2)中的图象,探究该函数的性质.
①该函数的最大值为________;
②若方程有两个解,则k的取值范围是________;
③请你再写出一条该函数的性质.
20.如图,小明对自己家所在小区进行调查后发现,小区车库入口宽为,在入口的一侧安装了起落杆,其中为支架,当起落杆仰起并与地面成角时,起落杆的端点C恰好与地面接触,此时为.在此状态下,若一辆货车高,宽,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗 请你通过计算说明.(参考数据:)
21.“书香中国,读领未来”,4月23日是世界读书日,我市某书店同时购进,两类图书,已知购进3本类图书和4本类图书共需192元;购进6本类图书和2本类图书共需240元.
(1),两类图书每本的进价各是多少元?
(2)该书店计划恰好用元来购进这两类图书,设购进类本,类本.
①求关于的关系式.
②进货时,类图书的购进数量不少于500本,已知类图书每本的售价为38元,类图书每本的售价为30元,如何进货才能使书店所获利润最大?最大利润为多少元?
22.如图,已知一次函数的图象与x轴,y轴分别交于,两点,与直线交于点C.
(1)求一次函数的解析式;
(2)在x轴上有一点,过点P作x轴的垂线,与直线交于点E,与直线交于点F,若,求m的值;
(3)点M为射线上一动点,点N为直线上一动点,是否存在点M,N使得是以点M为直角顶点的等腰直角三角形.若存在,求出点M的坐标;若不存在,请说明理由.
23.问题情景:在数学活动课上:老师出示了这样一个问题:如图①,在正方形中,,分别是射线,上的点,且,点在射线上,且满足.
数学思考:
(1)如图①,当点,,分别在线段,,上时,线段与的数量关系为________;位置关系为________;
猜想证明:
(2)如图②,当点,,分别在线段,,的延长线上时,()中的结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
拓展延伸:
(3)若,当时,请直接写出线段的长度.
参考答案
1.C
,被开方数为,当时,,此时式子无意义,因此不一定是二次根式,故选项A错误;
,被开方数为,负数在实数范围内无法开平方,故不是二次根式,故选项B错误;
,被开方数是正数,且根指数为2,符合二次根式定义,因此一定是二次根式,故选项C正确;
,根指数为3,属于三次根式,不符合二次根式条件,故选项D错误
故答案为:C.
2.D
解:A、,故A错误,不符合题意;
B、与为不同类二次根式,无法合并,故B错误,不符合题意;
C、,故C错误,不符合题意;
D、,故D正确,符合题意;
故选:D.
3.B
解: ①:每个x对应唯一y,是函数.
②:每个x对应唯一y,是函数.
③:解为 ,一个x对应两个y,不是函数.
④:平方根仅取非负值,每个x对应唯一y,是函数.
⑤:解为 ,一个x对应两个y,不是函数.
⑥:每个x对应唯一y,是函数.
∴y是x的函数的有①②④⑥。
故选:B.
4.A
由点P坐标为(-2,3),
可知OP=,
又因为OA=OP,
所以A的横坐标为-,介于-4和-3之间,
故选A.
5.B
解:原数据为24,26,28,29,29,31.
众数:原众数为29,四年后变为33,改变(A错误).
方差:各数同加4,数据波动性不变,方差不变(B正确).
平均数:原平均数为,四年后增加4,变为,改变(C错误).
中位数:原中位数为,四年后变为,改变(D错误).
故选B.
6.B
解:A选项:
∵∠ABD=∠BDC,OA=OC,∠AOB=∠COD,
∴△AOB≌△COD(AAS),
∴DO=BO,
∵,,
∴四边形ABCD是平行四边形,故A选项不合题意;
B选项:
在与,
,,
这是SSA模型,不能判定,
因此,也不能用来判定四边形ABCD是平行四边形;
下图给出一个反例,图中,
则满足条件:,,但四边形ABCD不是平行四边形,
故B符合题意;
C选项:
∵ADBC,
∴∠OAD=∠OCB,∠ODA=∠OBC,
∵,
∴△OAD≌△OCB,
∴,
∵,,
∴四边形ABCD是平行四边形,故C选项不合题意;
D选项:
∵∠ABD=∠BDC,
∴ABCD.
又∵,
∴ADCB,
∴四边形ABCD是平行四边形,故D选项不合题意;
故选:B.
7.A
对于一次函数,
∵,
∴,
∴,
即一次函数的系数为负,
∴函数随的增大而减小.
∵,,中,
∴,
故选:A.
8.D
解:由图象可知,,,故选项A、C正确,不符合题意;
直线与直线的交点的横坐标为,即方程的解是,故选项B正确,不符合题意;
根据图象可知,不等式的解集是,故选项D错误,符合题意.
故选D.
9.B
解:∵,,
∴,,
∵四边形为矩形,
∴,
根据作图可知:平分,
∴,
∴点H为的中点,
∵为的中点,
∴.
故选:B.
10.B
解:设点C平移的距离为x,正方形与重合部分的面积为y,
∴当时,如图:
∴;
当时,如图:
∴;
∴,
由分段函数可看出B选项中的函数图象与所求的分段函数对应,
故选:B.
11.x≥-2且x≠1
解:由题意可得
解得x≥-2且x≠1
故答案为:x≥-2且x≠1.
12.
解:一次函数的图象是由直线向左平移2个单位长度得到,
.
故答案为:.
13.86分
解:(分),
答:小桐这学期的体育成绩是86分.
故答案是:86分
14./45度
解:如图,作点关于线段的对称点,连接,
由对称可得,
即,
设小正方形的边长为 1 ,
由勾股定理,得,
,
是等腰直角三角形,
∴,即.
故答案为:.
15.
解:过作于,
四边形是菱形,
,,,,平分,
于,
,
,,,
当P、、共线时,,此时有最小值,即的长度
,,
,,
,
菱形的面积,
,
.
的值为.
故答案为:.
16.(1)
(2)
(1)解:原式
;
(2)解:原式
.
17.(1),
(2)八
(3)九年级的学生体育锻炼情况总体更好,理由见解析
(1)解:将八年级学生的平均每周锻炼时长数据从小到大排序:5,6,6,7,7,8, 8,9, 11, 13,
所以中位数;
由九年级学生平均每周锻炼时长数据的条形统计图可知.
故答案为:,.
(2)解:平均每周锻炼时长是8小时,在八年级排第4,在九年级排第6,所以杨洋是八年级学生.
故答案为:八.
(3)解:九年级的学生体育锻炼情况总体更好.理由如下(答案不唯一):
①中位数来看,九年级(小时)高于八年级(小时),表明九年级一半以上的学生达到较高锻炼时长;
②从方差来看,九年级方差()小于八年级(),说明九年级数据更集中,波动更小.
18.(1)见解析
(2)见解析
(1)解: 图形如图所示:
(2)证明: ,
,
四边形是菱形,
, , ,
,
,
,
又,
四边形为平行四边形,
,
,
,
,
四边形为矩形.
19.(1),
(2)见解析
(3)①1;②;③根据图象可知,当时,y随x的增大而大;当时,y随x的增大而减小
(1)解:当时,,
当时,,
故答案为:,;
(2)解:函数图象如下:
(3)解:①根据函数图象,该函数的最大值为;
②根据函数图象,若方程有两个解,则k的取值范围是;
③当时,y随x的增大而大;当时,y随x的增大而减小.
20.不能,理由见解析
解:不能.
理由如下:在之间找一点F,使,
过点F作,交于点G,
如图所示,
,,,
.
,,
,
在中,由勾股定理得,
,
,
,
这辆货车在不碰杆的情况下,不能从入口内通过.
,
这辆货车在不碰杆的情况下,不能从入口内通过.
21.(1),两类图书每本的进价分别为32元,24元
(2)①,②当购进类图书501本,类图书1332本时,书店所获利润最大,最大利润为10998元
(1)解:设,两类图书每本的进价分别为元,元.
,解得
答:,两类图书每本的进价分别为32元,24元.
(2)①依题意;
∴
②解得
设利润为元.
因为小于0,所以随的增大而减小,
当取501时,
,
所以当购进类图书501本,类图书1332本时,书店所获利润最大,最大利润为10998元.
22.(1)
(2)或8
(3)或
(1)解:依题意,把,代入得到
解得,
∴一次函数的解析式是
(2)解:∵在x轴上有一点,过点P作x轴的垂线,与直线交于点E,与直线交于点F,
∴,,
∵,
∴,
,
,
则或,
或;
(3)解:或,过程如下:
依题意,联立方程组,
解得,
点C坐标
在x轴上取一点M,在直线上取一点N,使得,且,分别过N,C作x轴的垂线,垂足为H,I.
第一种情况,当点在的延长线上时,如图所示:
∵是以点M为直角顶点的等腰直角三角形,
,
,
又,
,
,,
设,
则
,
把点代入,
得,
解得;
第二种情况:当点在线段上时,
∵是以点M为直角顶点的等腰直角三角形,
,
,
又,
,
,,
设,则
,
把点代入,
得,
解得,
综上所述或.
23.(1),;(2),,依然成立,证明见解析;(3)或
(1)如图所示,过点作于点,设交于点,
∵
∴,
∵四边形是正方形,
∴,,
又∵,
∴
∴,,
又
又
又∵,
(2),,依然成立,证明如下,
如图所示,过点作于点,延长交于点,
∵
∴,
∵四边形是正方形,
∴,,
又∵,
∴
∴,,
又
又
又∵,
(3)当点,,分别在线段,,上时,同(1)可得
∴
∵,
∴,
∴
∴;
当点,,分别在线段,,的延长线上时,由(2)可得
∵,,
∴,
∴.
一、单选题
1.下列各式一定是二次根式的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.下列关系式中:①;②;③;④;⑤;⑥,其中y是x的函数的有( )
A.3个 B.4个 C.5个 D.6个
4.如图,在平面直角坐标系中,点P坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.-4和-3之间 B.3和4之间 C.-5和-4之间 D.4和5之间
5.河南省曲剧团中六位曲剧演员的年龄(单位:岁)分别为26,24,29,31,28,29,则四年后这六位曲剧演员的年龄数据中一定不会改变的是( )
A.众数 B.方差 C.平均数 D.中位数
6.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A., B.,
C., D.,
7.已知点,点是上的两点,则与的大小关系是( )
A. B. C. D.
8.如图,已知直线与直线的交点的横坐标为,根据图象,下列结论中错误的是( )
A. B.方程的解是
C. D.不等式的解集是
9.如图,在矩形中,对角线,相交于点D,以点D为圆心,任意长为半径画弧,分别交,于点E,F,再分别以E,F为圆心,大于的长为半径画弧,两弧交于点G,连接并延长,交于点H,已知,则的长为( )
A. B.4 C.5 D.6
10.如图,与正方形的一条边重合,,,将正方形沿向右平移,当点D与点A重合时,停止平移,设点C平移的距离为x,正方形与重合部分的面积为y,则y关于x的函数图象大致为( )
A. B. C. D.
二、填空题
11.函数中,自变量x的取值范围是 .
12.已知一次函数的图象是由直线向左平移2个单位长度得到,则该函数解析式是 .
13.某中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占20%,其中考试成绩占30%,期末考试成绩占50%,小桐的三项成绩(百分制)依次是80,90,86,则小桐这学期的体育成绩是 .
14.如图,点A,B,C,D均在正方形网格格点上,则 .
15.如图,在菱形中,对角线与相交于点O,P是上任一点,于E,于F,若,,则的最小值为 .
三、解答题
16.计算:
(1)
(2)
17.为了解学生的体育锻炼情况,学校以“活跃校园——探索初中生的运动生活”为主题开展调查研究.通过问卷,收集了八、九年级学生的平均每周锻炼时长数据,现从两个年级分别随机抽取10名学生的平均每周锻炼时长(单位:小时)进行整理、描述和分析,下面给出部分信息.
【数据收集】
八年级:9,7,11,8,7,5,6,8,6,13;
九年级学生平均每周锻炼时长数据的条形统计图如下:
【数据整理、分析】
年级 平均数 中位数 众数 方差
八年级 8 a 8
九年级 8 b
根据以上信息,回答下列问题:
(1)填空:________,________;
(2)杨洋对李刚说:“虽然平均每周锻炼时长我俩都是8小时,但我在我们年级中的排名比你在你们年级的排名靠前.”观察上表可知,杨洋是________年级学生.(填“八”或“九”)
(3)你认为哪个年级的学生体育锻炼情况的总体水平较好?请给出两条理由.
18.如图,小橘子数学研修活动中做了以下探究:在菱形中,对角线、相交于点.
(1)尺规作图:在的延长线上截取,连接,再过点 作的垂线交于点 (保留作图痕迹,不写作法);
(2)求证: 四边形为矩形.
19.研究新函数,可以通过一次函数的图象和性质的学习过程来探究新函数.
(1)补全下表:
x … 0 1 2 3 …
y … ________ 1 ________
(2)根据(1)中的数据在下图中画出函数图象;
(3)根据(2)中的图象,探究该函数的性质.
①该函数的最大值为________;
②若方程有两个解,则k的取值范围是________;
③请你再写出一条该函数的性质.
20.如图,小明对自己家所在小区进行调查后发现,小区车库入口宽为,在入口的一侧安装了起落杆,其中为支架,当起落杆仰起并与地面成角时,起落杆的端点C恰好与地面接触,此时为.在此状态下,若一辆货车高,宽,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗 请你通过计算说明.(参考数据:)
21.“书香中国,读领未来”,4月23日是世界读书日,我市某书店同时购进,两类图书,已知购进3本类图书和4本类图书共需192元;购进6本类图书和2本类图书共需240元.
(1),两类图书每本的进价各是多少元?
(2)该书店计划恰好用元来购进这两类图书,设购进类本,类本.
①求关于的关系式.
②进货时,类图书的购进数量不少于500本,已知类图书每本的售价为38元,类图书每本的售价为30元,如何进货才能使书店所获利润最大?最大利润为多少元?
22.如图,已知一次函数的图象与x轴,y轴分别交于,两点,与直线交于点C.
(1)求一次函数的解析式;
(2)在x轴上有一点,过点P作x轴的垂线,与直线交于点E,与直线交于点F,若,求m的值;
(3)点M为射线上一动点,点N为直线上一动点,是否存在点M,N使得是以点M为直角顶点的等腰直角三角形.若存在,求出点M的坐标;若不存在,请说明理由.
23.问题情景:在数学活动课上:老师出示了这样一个问题:如图①,在正方形中,,分别是射线,上的点,且,点在射线上,且满足.
数学思考:
(1)如图①,当点,,分别在线段,,上时,线段与的数量关系为________;位置关系为________;
猜想证明:
(2)如图②,当点,,分别在线段,,的延长线上时,()中的结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
拓展延伸:
(3)若,当时,请直接写出线段的长度.
参考答案
1.C
,被开方数为,当时,,此时式子无意义,因此不一定是二次根式,故选项A错误;
,被开方数为,负数在实数范围内无法开平方,故不是二次根式,故选项B错误;
,被开方数是正数,且根指数为2,符合二次根式定义,因此一定是二次根式,故选项C正确;
,根指数为3,属于三次根式,不符合二次根式条件,故选项D错误
故答案为:C.
2.D
解:A、,故A错误,不符合题意;
B、与为不同类二次根式,无法合并,故B错误,不符合题意;
C、,故C错误,不符合题意;
D、,故D正确,符合题意;
故选:D.
3.B
解: ①:每个x对应唯一y,是函数.
②:每个x对应唯一y,是函数.
③:解为 ,一个x对应两个y,不是函数.
④:平方根仅取非负值,每个x对应唯一y,是函数.
⑤:解为 ,一个x对应两个y,不是函数.
⑥:每个x对应唯一y,是函数.
∴y是x的函数的有①②④⑥。
故选:B.
4.A
由点P坐标为(-2,3),
可知OP=,
又因为OA=OP,
所以A的横坐标为-,介于-4和-3之间,
故选A.
5.B
解:原数据为24,26,28,29,29,31.
众数:原众数为29,四年后变为33,改变(A错误).
方差:各数同加4,数据波动性不变,方差不变(B正确).
平均数:原平均数为,四年后增加4,变为,改变(C错误).
中位数:原中位数为,四年后变为,改变(D错误).
故选B.
6.B
解:A选项:
∵∠ABD=∠BDC,OA=OC,∠AOB=∠COD,
∴△AOB≌△COD(AAS),
∴DO=BO,
∵,,
∴四边形ABCD是平行四边形,故A选项不合题意;
B选项:
在与,
,,
这是SSA模型,不能判定,
因此,也不能用来判定四边形ABCD是平行四边形;
下图给出一个反例,图中,
则满足条件:,,但四边形ABCD不是平行四边形,
故B符合题意;
C选项:
∵ADBC,
∴∠OAD=∠OCB,∠ODA=∠OBC,
∵,
∴△OAD≌△OCB,
∴,
∵,,
∴四边形ABCD是平行四边形,故C选项不合题意;
D选项:
∵∠ABD=∠BDC,
∴ABCD.
又∵,
∴ADCB,
∴四边形ABCD是平行四边形,故D选项不合题意;
故选:B.
7.A
对于一次函数,
∵,
∴,
∴,
即一次函数的系数为负,
∴函数随的增大而减小.
∵,,中,
∴,
故选:A.
8.D
解:由图象可知,,,故选项A、C正确,不符合题意;
直线与直线的交点的横坐标为,即方程的解是,故选项B正确,不符合题意;
根据图象可知,不等式的解集是,故选项D错误,符合题意.
故选D.
9.B
解:∵,,
∴,,
∵四边形为矩形,
∴,
根据作图可知:平分,
∴,
∴点H为的中点,
∵为的中点,
∴.
故选:B.
10.B
解:设点C平移的距离为x,正方形与重合部分的面积为y,
∴当时,如图:
∴;
当时,如图:
∴;
∴,
由分段函数可看出B选项中的函数图象与所求的分段函数对应,
故选:B.
11.x≥-2且x≠1
解:由题意可得
解得x≥-2且x≠1
故答案为:x≥-2且x≠1.
12.
解:一次函数的图象是由直线向左平移2个单位长度得到,
.
故答案为:.
13.86分
解:(分),
答:小桐这学期的体育成绩是86分.
故答案是:86分
14./45度
解:如图,作点关于线段的对称点,连接,
由对称可得,
即,
设小正方形的边长为 1 ,
由勾股定理,得,
,
是等腰直角三角形,
∴,即.
故答案为:.
15.
解:过作于,
四边形是菱形,
,,,,平分,
于,
,
,,,
当P、、共线时,,此时有最小值,即的长度
,,
,,
,
菱形的面积,
,
.
的值为.
故答案为:.
16.(1)
(2)
(1)解:原式
;
(2)解:原式
.
17.(1),
(2)八
(3)九年级的学生体育锻炼情况总体更好,理由见解析
(1)解:将八年级学生的平均每周锻炼时长数据从小到大排序:5,6,6,7,7,8, 8,9, 11, 13,
所以中位数;
由九年级学生平均每周锻炼时长数据的条形统计图可知.
故答案为:,.
(2)解:平均每周锻炼时长是8小时,在八年级排第4,在九年级排第6,所以杨洋是八年级学生.
故答案为:八.
(3)解:九年级的学生体育锻炼情况总体更好.理由如下(答案不唯一):
①中位数来看,九年级(小时)高于八年级(小时),表明九年级一半以上的学生达到较高锻炼时长;
②从方差来看,九年级方差()小于八年级(),说明九年级数据更集中,波动更小.
18.(1)见解析
(2)见解析
(1)解: 图形如图所示:
(2)证明: ,
,
四边形是菱形,
, , ,
,
,
,
又,
四边形为平行四边形,
,
,
,
,
四边形为矩形.
19.(1),
(2)见解析
(3)①1;②;③根据图象可知,当时,y随x的增大而大;当时,y随x的增大而减小
(1)解:当时,,
当时,,
故答案为:,;
(2)解:函数图象如下:
(3)解:①根据函数图象,该函数的最大值为;
②根据函数图象,若方程有两个解,则k的取值范围是;
③当时,y随x的增大而大;当时,y随x的增大而减小.
20.不能,理由见解析
解:不能.
理由如下:在之间找一点F,使,
过点F作,交于点G,
如图所示,
,,,
.
,,
,
在中,由勾股定理得,
,
,
,
这辆货车在不碰杆的情况下,不能从入口内通过.
,
这辆货车在不碰杆的情况下,不能从入口内通过.
21.(1),两类图书每本的进价分别为32元,24元
(2)①,②当购进类图书501本,类图书1332本时,书店所获利润最大,最大利润为10998元
(1)解:设,两类图书每本的进价分别为元,元.
,解得
答:,两类图书每本的进价分别为32元,24元.
(2)①依题意;
∴
②解得
设利润为元.
因为小于0,所以随的增大而减小,
当取501时,
,
所以当购进类图书501本,类图书1332本时,书店所获利润最大,最大利润为10998元.
22.(1)
(2)或8
(3)或
(1)解:依题意,把,代入得到
解得,
∴一次函数的解析式是
(2)解:∵在x轴上有一点,过点P作x轴的垂线,与直线交于点E,与直线交于点F,
∴,,
∵,
∴,
,
,
则或,
或;
(3)解:或,过程如下:
依题意,联立方程组,
解得,
点C坐标
在x轴上取一点M,在直线上取一点N,使得,且,分别过N,C作x轴的垂线,垂足为H,I.
第一种情况,当点在的延长线上时,如图所示:
∵是以点M为直角顶点的等腰直角三角形,
,
,
又,
,
,,
设,
则
,
把点代入,
得,
解得;
第二种情况:当点在线段上时,
∵是以点M为直角顶点的等腰直角三角形,
,
,
又,
,
,,
设,则
,
把点代入,
得,
解得,
综上所述或.
23.(1),;(2),,依然成立,证明见解析;(3)或
(1)如图所示,过点作于点,设交于点,
∵
∴,
∵四边形是正方形,
∴,,
又∵,
∴
∴,,
又
又
又∵,
(2),,依然成立,证明如下,
如图所示,过点作于点,延长交于点,
∵
∴,
∵四边形是正方形,
∴,,
又∵,
∴
∴,,
又
又
又∵,
(3)当点,,分别在线段,,上时,同(1)可得
∴
∵,
∴,
∴
∴;
当点,,分别在线段,,的延长线上时,由(2)可得
∵,,
∴,
∴.
同课章节目录
