甘肃省武威第二十七中学2024-2025学年第二学期七年级数学新人教版期末试卷(含答案)
文档属性
| 名称 | 甘肃省武威第二十七中学2024-2025学年第二学期七年级数学新人教版期末试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 866.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 15:11:10 | ||
图片预览




文档简介
甘肃省武威第二十七中学2024-2025学年第二学期七年级数学新人教版期末试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)已知一个数的两个平方根分别是和,则这个数是( ).
A. B. C. D.
2.(本题3分)如图,在平面直角坐标系中,点A的坐标为( )
A. B. C. D.
3.(本题3分)已知实数满足,那么的值为( )
A. B.1 C. D.2
4.(本题3分)2025年2月,河南省教育厅发布《关于全省义务教育阶段学校每天开展两小时综合体育活动的通知》,为丰富学生的课间体育活动,某中学开设了四个体育活动社团,分别是篮球社团、足球社团、乒乓球社团和羽毛球社团.学校为了解学生最喜欢的体育社团是哪一个,随机调查了部分学生(每人必选且只能选1个社团),并将调查结果绘制成如下的扇形统计图,已知最喜欢羽毛球社团的学生有20人,下列说法不正确的是( )
A.最喜欢羽毛球社团的人数占被调查人数的 B.被调查的人数一共有200人
C.被调查的人中最喜欢足球社团的有30人 D.被调查的人中最喜欢篮球社团的人数最多
5.(本题3分)如果单项式与单项式的和仍是一个单项式,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(本题3分)方程组的解中,x的值比y的值大1,则k为 ( )
A. B.- C.2 D.-2
7.(本题3分)下面是老师在黑板上展示的某同学用代入消元法方程组的步骤,其中开始出现错误的是( )
A.步骤一 B.步骤二 C.步骤三 D.步骤四
8.(本题3分)A,B,C,D,E五名学生猜测自己能否进入市中国象棋前三强.A说:“如果我进入,那么B也进入.”B说:“如果我进入,那么C也进入.”C说:“如果我进入,那么D也进入.”D说:“如果我进入,那么E也进入,”大家都没有说错,则进入前三强的三个人是( )
A.A,B,C B.B,C,D C.D,E,A D.C,D,E
9.(本题3分)在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地锦”,如图1,计算,将乘数82记入上行,乘数34记入右行,然后用乘数82的每位数字乘以乘数34的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2788.如图2,用“铺地锦”的方法表示两个两位数相乘,下列结论错误的是( )
A.b的值为6
B.a为奇数
C.乘积结果可以表示为
D.a的值小于3
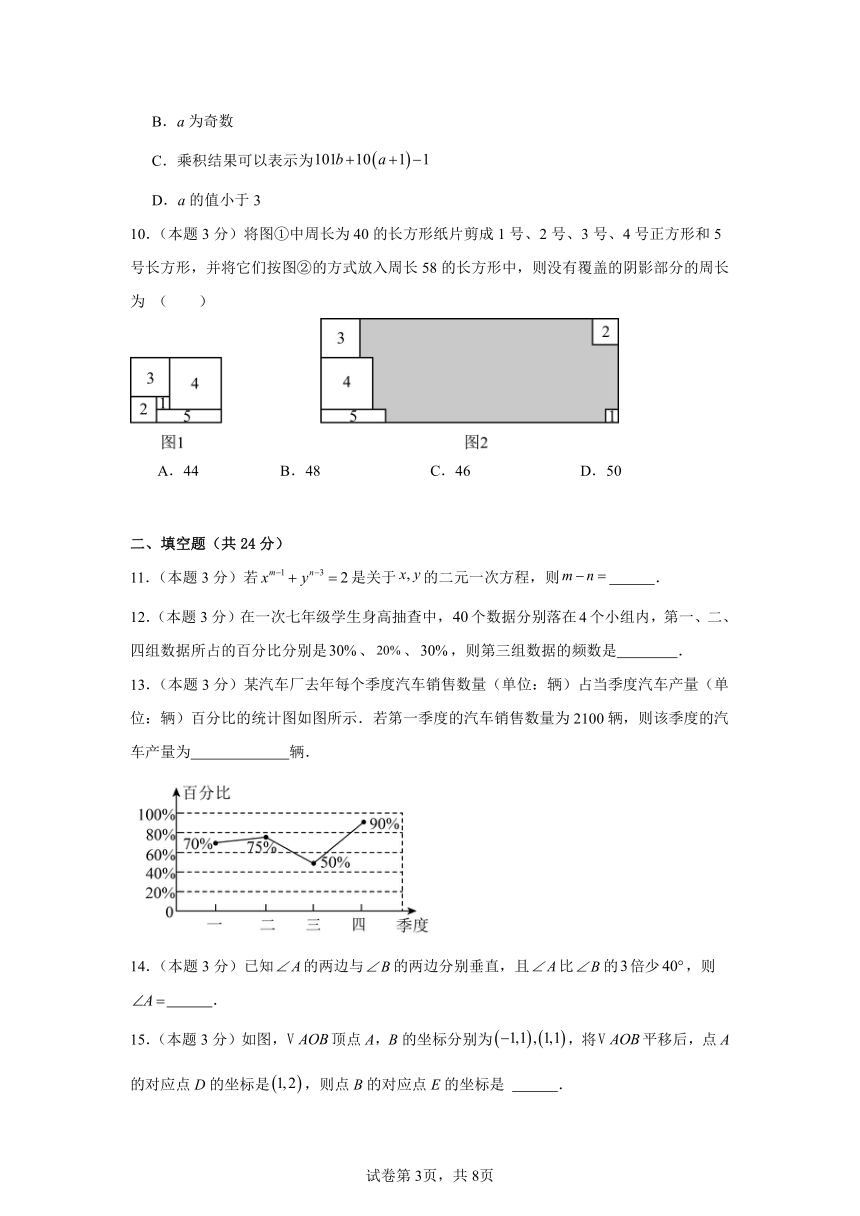
10.(本题3分)将图①中周长为40的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图②的方式放入周长58的长方形中,则没有覆盖的阴影部分的周长为 ( )
A.44 B.48 C.46 D.50
二、填空题(共24分)
11.(本题3分)若是关于的二元一次方程,则 .
12.(本题3分)在一次七年级学生身高抽查中,个数据分别落在个小组内,第一、二、四组数据所占的百分比分别是、、,则第三组数据的频数是 .
13.(本题3分)某汽车厂去年每个季度汽车销售数量(单位:辆)占当季度汽车产量(单位:辆)百分比的统计图如图所示.若第一季度的汽车销售数量为2100辆,则该季度的汽车产量为 辆.
14.(本题3分)已知的两边与的两边分别垂直,且比的倍少,则 .
15.(本题3分)如图,顶点A,B的坐标分别为,将平移后,点A的对应点D的坐标是,则点B的对应点E的坐标是 .
16.(本题3分)某学校为了解ZS中学4000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时)
人数 7 10 14 19
17.(本题3分)如图是一个海螺,它有一定的数学形态美,我们把它抽象出来变成数学中的一个小模型;如图(1),若点H在的边上,且满足(或),则称满足这样条件的点为边上的“海螺点”.
如图(2),在中,,且,若点是边上的“海螺点”,则 .
如图(3),直角坐标系中,点,在x轴存在点H使点A为边的“海螺点”,则点H的坐标为 .
18.(本题3分)秋季泡脚,睡前养生,9月份某商场从工厂进货了中药包、精油球和足浴液这三种类型的泡脚材料,数量之比为,中药包与精油球单价之比为,足浴液的单价是精油球的2倍,由于天气骤冷,足浴液销售火爆,月份工厂对这三种泡脚材料的价格进行了调整,该商场也相应调整了进货量,相较于9月,商场采购中药包增加的费用占月所有泡脚材料采购费用的且月采购中药包与精油球的总费用之比为,采购精油球、足浴液增加的费用之比为,则精油球9月份与月份的采购总费用之比为 .
三、解答题(共66分)
19.(本题4分)计算:.
20.(本题4分)计算:.
21.(本题8分)解方程(组).
(1)
(2)
22.(本题8分)解不等式(组):
(1);
(2).
23.(本题6分)如图,点、的坐标分别为、.将绕点按逆时针方向旋转得到.
(1)画出:
(2)写出点、的坐标.
24.(本题6分)为了培养学生的爱国主义情怀,激发青少年报效祖国、奉献社会、服务人民的责任心和使命感,学校举办了“小小贺卡,军民情深”祝福活动.小芳制作了一张面积为的正方形贺卡.现有一个长方形信封如图所示,长、宽之比为,面积为,小芳能将这张贺卡不折叠就放入此信封吗?请通过计算说明你的判断.
25.(本题6分)某礼品店为迎接农历新年的到来,准备购进一批适合学生的礼品.已知购进4件A礼品和12件B礼品共需360元,购进8件A礼品和6件B礼品共需270元.
(1)(列二元一次方程组)求A,B两种礼品每件的进价.
(2)该店计划将5000元全部用于购进A,B这两种礼品,设购进A礼品m件,B礼品n件.
①求n与m之间的关系式;
②该店进货时,厂家要求A礼品的购进数量不少于100件.已知A礼品每件售价为20元,B礼品每件售价为35元.设该店全部售出这两种礼品可获利W元,求W与m之间的关系式和该店所获利润的最大值.
26.(本题8分)综合与探究:
已知直线,点A是a上的动点,点B在a上(点A不与点B重合),点C、D在b上,且点C在点D左侧,的平分线相交于点E.
(1)如图1所示,若点A在点B的左侧,,过点E作,求的度数;
(2)如图2所示,若点A在点B的左侧,,则___________(用含、的式子表示);
(3)如图3所示,若点A在点B的右侧,,求的度数(用含的式子表示).
27.(本题8分)下面是小明同学解一元一次不等式的过程,请认真阅读并完成相应的任务.
解:去分母,得.……………………………………第一步 移项,得.………………………………………第二步 合并同类项,得.……………………………………………第三步 化系数为1,得.……………………………………………………第四步
(1)去分母的依据是______;
(2)解答过程中,从前一步到后一步的变形,共出现______处错误,其中最后一处错误在第______步,错误的原因是______;
(3)请写出不等式的正确解答过程,并把解集表示在数轴上;
28.(本题8分)七年级某班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
用均用水量 频数(户) 频率
6 0.12
0.24
16 0.32
10 0.20
4
2 0.04
请解答以下问题:
(1)这里采用的调查方式是__________(填“普查”或“抽样调查”),样本容量是__________;
(2)填空:__________,__________,并把频数分布直方图补充完整;
(3)若将抽取的部分家庭月均用水量的频数绘成扇形统计图,求出月均用水量“”所对应的扇形的圆心角的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B C B A C D D B
11.
12.8
13.3000
14.或
15.
16.1360
17. 或
18.
19.
20.
21.(1)解:
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化1,得;
(2)解:方程组整理,得
由,得,
解得,
将代入①,得,
解得,
原方程组的解为.
22.(1)解:
去括号,得:,
移项,得:,
系数化为1,得:;
(2)
解不等式①得:,
解不等式②得:,
则原不等式组的解集为.
23.(1)解:将点、点的坐标分别绕点按逆时针方向旋转,得到对应点、,顺次连接各点即可得到,如图所示:
;
(2)解:由图可知:
点的坐标为,点的坐标为.
24.小芳能将这张贺卡不折叠就放入此信封,理由如下:
设长方形信封的长为,宽为,
长方形面积为,
,
,
解得,
长方形的宽为,
正方形贺卡的面积为,
正方形贺卡的边长为,
,
,
,
小芳能将这张贺卡不折叠就放入此信封.
25.(1)设A礼品每个的进价是x元,B礼品每个的进价是y元,
依题意得,,
解得,
故A礼品每个的进价是15元,B礼品每个的进价是25元;.
(2)(2)①依题意得,,
∴.
②∵W表示所获得的利润,
∴,
∵,
∴W随m的增大而减小,
∵,
∴当时,W取得最大值.即A礼品进货100件时,该店获利最大,
最大利润为, (元).
26.(1)解:、分别是,的平分线,
,,
∵,
,
∵,
∴,
,
;
(2)解:过点E作,
、分别是,的平分线,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:;
(3)解:过点向右作,
,分别是、的平分线,
,,
∵,
又∵,
∴,
,
.
27.(1)解:去分母的依据是不等式的性质2;
(2)解:三,四,不等式的两边同除以时不等号方向未改变;
(3)解:,
去分母,得,
移项,得,
合并同类项,得,
化系数为1,得,
这个不等式的解集在数轴上表示如下图:
28.(1)解:这里采用的调查方式是抽样调查,
∵被调查的总户数为(户),
∴样本容量是50;
故答案为:抽样调查,50;
(2)解:,;
故答案为:12,0.08;
补全频数分布直方图如下:
(3)解:月均用水量“”所对应的扇形的圆心角的度数是;
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共30分)
1.(本题3分)已知一个数的两个平方根分别是和,则这个数是( ).
A. B. C. D.
2.(本题3分)如图,在平面直角坐标系中,点A的坐标为( )
A. B. C. D.
3.(本题3分)已知实数满足,那么的值为( )
A. B.1 C. D.2
4.(本题3分)2025年2月,河南省教育厅发布《关于全省义务教育阶段学校每天开展两小时综合体育活动的通知》,为丰富学生的课间体育活动,某中学开设了四个体育活动社团,分别是篮球社团、足球社团、乒乓球社团和羽毛球社团.学校为了解学生最喜欢的体育社团是哪一个,随机调查了部分学生(每人必选且只能选1个社团),并将调查结果绘制成如下的扇形统计图,已知最喜欢羽毛球社团的学生有20人,下列说法不正确的是( )
A.最喜欢羽毛球社团的人数占被调查人数的 B.被调查的人数一共有200人
C.被调查的人中最喜欢足球社团的有30人 D.被调查的人中最喜欢篮球社团的人数最多
5.(本题3分)如果单项式与单项式的和仍是一个单项式,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.(本题3分)方程组的解中,x的值比y的值大1,则k为 ( )
A. B.- C.2 D.-2
7.(本题3分)下面是老师在黑板上展示的某同学用代入消元法方程组的步骤,其中开始出现错误的是( )
A.步骤一 B.步骤二 C.步骤三 D.步骤四
8.(本题3分)A,B,C,D,E五名学生猜测自己能否进入市中国象棋前三强.A说:“如果我进入,那么B也进入.”B说:“如果我进入,那么C也进入.”C说:“如果我进入,那么D也进入.”D说:“如果我进入,那么E也进入,”大家都没有说错,则进入前三强的三个人是( )
A.A,B,C B.B,C,D C.D,E,A D.C,D,E
9.(本题3分)在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地锦”,如图1,计算,将乘数82记入上行,乘数34记入右行,然后用乘数82的每位数字乘以乘数34的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2788.如图2,用“铺地锦”的方法表示两个两位数相乘,下列结论错误的是( )
A.b的值为6
B.a为奇数
C.乘积结果可以表示为
D.a的值小于3
10.(本题3分)将图①中周长为40的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图②的方式放入周长58的长方形中,则没有覆盖的阴影部分的周长为 ( )
A.44 B.48 C.46 D.50
二、填空题(共24分)
11.(本题3分)若是关于的二元一次方程,则 .
12.(本题3分)在一次七年级学生身高抽查中,个数据分别落在个小组内,第一、二、四组数据所占的百分比分别是、、,则第三组数据的频数是 .
13.(本题3分)某汽车厂去年每个季度汽车销售数量(单位:辆)占当季度汽车产量(单位:辆)百分比的统计图如图所示.若第一季度的汽车销售数量为2100辆,则该季度的汽车产量为 辆.
14.(本题3分)已知的两边与的两边分别垂直,且比的倍少,则 .
15.(本题3分)如图,顶点A,B的坐标分别为,将平移后,点A的对应点D的坐标是,则点B的对应点E的坐标是 .
16.(本题3分)某学校为了解ZS中学4000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时)
人数 7 10 14 19
17.(本题3分)如图是一个海螺,它有一定的数学形态美,我们把它抽象出来变成数学中的一个小模型;如图(1),若点H在的边上,且满足(或),则称满足这样条件的点为边上的“海螺点”.
如图(2),在中,,且,若点是边上的“海螺点”,则 .
如图(3),直角坐标系中,点,在x轴存在点H使点A为边的“海螺点”,则点H的坐标为 .
18.(本题3分)秋季泡脚,睡前养生,9月份某商场从工厂进货了中药包、精油球和足浴液这三种类型的泡脚材料,数量之比为,中药包与精油球单价之比为,足浴液的单价是精油球的2倍,由于天气骤冷,足浴液销售火爆,月份工厂对这三种泡脚材料的价格进行了调整,该商场也相应调整了进货量,相较于9月,商场采购中药包增加的费用占月所有泡脚材料采购费用的且月采购中药包与精油球的总费用之比为,采购精油球、足浴液增加的费用之比为,则精油球9月份与月份的采购总费用之比为 .
三、解答题(共66分)
19.(本题4分)计算:.
20.(本题4分)计算:.
21.(本题8分)解方程(组).
(1)
(2)
22.(本题8分)解不等式(组):
(1);
(2).
23.(本题6分)如图,点、的坐标分别为、.将绕点按逆时针方向旋转得到.
(1)画出:
(2)写出点、的坐标.
24.(本题6分)为了培养学生的爱国主义情怀,激发青少年报效祖国、奉献社会、服务人民的责任心和使命感,学校举办了“小小贺卡,军民情深”祝福活动.小芳制作了一张面积为的正方形贺卡.现有一个长方形信封如图所示,长、宽之比为,面积为,小芳能将这张贺卡不折叠就放入此信封吗?请通过计算说明你的判断.
25.(本题6分)某礼品店为迎接农历新年的到来,准备购进一批适合学生的礼品.已知购进4件A礼品和12件B礼品共需360元,购进8件A礼品和6件B礼品共需270元.
(1)(列二元一次方程组)求A,B两种礼品每件的进价.
(2)该店计划将5000元全部用于购进A,B这两种礼品,设购进A礼品m件,B礼品n件.
①求n与m之间的关系式;
②该店进货时,厂家要求A礼品的购进数量不少于100件.已知A礼品每件售价为20元,B礼品每件售价为35元.设该店全部售出这两种礼品可获利W元,求W与m之间的关系式和该店所获利润的最大值.
26.(本题8分)综合与探究:
已知直线,点A是a上的动点,点B在a上(点A不与点B重合),点C、D在b上,且点C在点D左侧,的平分线相交于点E.
(1)如图1所示,若点A在点B的左侧,,过点E作,求的度数;
(2)如图2所示,若点A在点B的左侧,,则___________(用含、的式子表示);
(3)如图3所示,若点A在点B的右侧,,求的度数(用含的式子表示).
27.(本题8分)下面是小明同学解一元一次不等式的过程,请认真阅读并完成相应的任务.
解:去分母,得.……………………………………第一步 移项,得.………………………………………第二步 合并同类项,得.……………………………………………第三步 化系数为1,得.……………………………………………………第四步
(1)去分母的依据是______;
(2)解答过程中,从前一步到后一步的变形,共出现______处错误,其中最后一处错误在第______步,错误的原因是______;
(3)请写出不等式的正确解答过程,并把解集表示在数轴上;
28.(本题8分)七年级某班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
用均用水量 频数(户) 频率
6 0.12
0.24
16 0.32
10 0.20
4
2 0.04
请解答以下问题:
(1)这里采用的调查方式是__________(填“普查”或“抽样调查”),样本容量是__________;
(2)填空:__________,__________,并把频数分布直方图补充完整;
(3)若将抽取的部分家庭月均用水量的频数绘成扇形统计图,求出月均用水量“”所对应的扇形的圆心角的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B C B A C D D B
11.
12.8
13.3000
14.或
15.
16.1360
17. 或
18.
19.
20.
21.(1)解:
去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化1,得;
(2)解:方程组整理,得
由,得,
解得,
将代入①,得,
解得,
原方程组的解为.
22.(1)解:
去括号,得:,
移项,得:,
系数化为1,得:;
(2)
解不等式①得:,
解不等式②得:,
则原不等式组的解集为.
23.(1)解:将点、点的坐标分别绕点按逆时针方向旋转,得到对应点、,顺次连接各点即可得到,如图所示:
;
(2)解:由图可知:
点的坐标为,点的坐标为.
24.小芳能将这张贺卡不折叠就放入此信封,理由如下:
设长方形信封的长为,宽为,
长方形面积为,
,
,
解得,
长方形的宽为,
正方形贺卡的面积为,
正方形贺卡的边长为,
,
,
,
小芳能将这张贺卡不折叠就放入此信封.
25.(1)设A礼品每个的进价是x元,B礼品每个的进价是y元,
依题意得,,
解得,
故A礼品每个的进价是15元,B礼品每个的进价是25元;.
(2)(2)①依题意得,,
∴.
②∵W表示所获得的利润,
∴,
∵,
∴W随m的增大而减小,
∵,
∴当时,W取得最大值.即A礼品进货100件时,该店获利最大,
最大利润为, (元).
26.(1)解:、分别是,的平分线,
,,
∵,
,
∵,
∴,
,
;
(2)解:过点E作,
、分别是,的平分线,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:;
(3)解:过点向右作,
,分别是、的平分线,
,,
∵,
又∵,
∴,
,
.
27.(1)解:去分母的依据是不等式的性质2;
(2)解:三,四,不等式的两边同除以时不等号方向未改变;
(3)解:,
去分母,得,
移项,得,
合并同类项,得,
化系数为1,得,
这个不等式的解集在数轴上表示如下图:
28.(1)解:这里采用的调查方式是抽样调查,
∵被调查的总户数为(户),
∴样本容量是50;
故答案为:抽样调查,50;
(2)解:,;
故答案为:12,0.08;
补全频数分布直方图如下:
(3)解:月均用水量“”所对应的扇形的圆心角的度数是;
答案第1页,共2页
答案第1页,共2页
同课章节目录
