1.11有理数的乘方(预习衔接.含解析)-2025-2026学年七年级上册数学华东师大版(2024)
文档属性
| 名称 | 1.11有理数的乘方(预习衔接.含解析)-2025-2026学年七年级上册数学华东师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 81.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 16:04:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
新课预习衔接 有理数的乘方
一.选择题(共5小题)
1.(2024 鼓楼区校级开学)池塘里的睡莲的面积每天长大一倍,若经过13天就可以长满整个池塘,则这些睡莲长满半个池塘需要( )天.
A.6 B.7 C.10 D.12
2.(2024 宜兴市二模)若数a的平方等于16,那么数a可能是( )
A.2 B.﹣4 C.±4 D.±8
3.(2024 邵阳期末)(﹣2)4的相反数是( )
A.﹣8 B.﹣16 C. D.8
4.(2024 行唐县期末)下列可以表示7a的是( )
A. B.
C. D.
5.(2024 淮北期末)下列各组数中,相等的一组是( )
A.﹣(﹣1)与﹣|﹣1| B.﹣32与(﹣3)2
C.(﹣4)3与﹣43 D.与()2
二.填空题(共5小题)
6.(2024春 松江区期中)如果a,b满足(a+3)2+|b﹣2|=0,那么ab= .
7.(2024 辉县市期末)有以下各式:①﹣|﹣2|;②﹣22;③(﹣3)2,其中负数有 个.
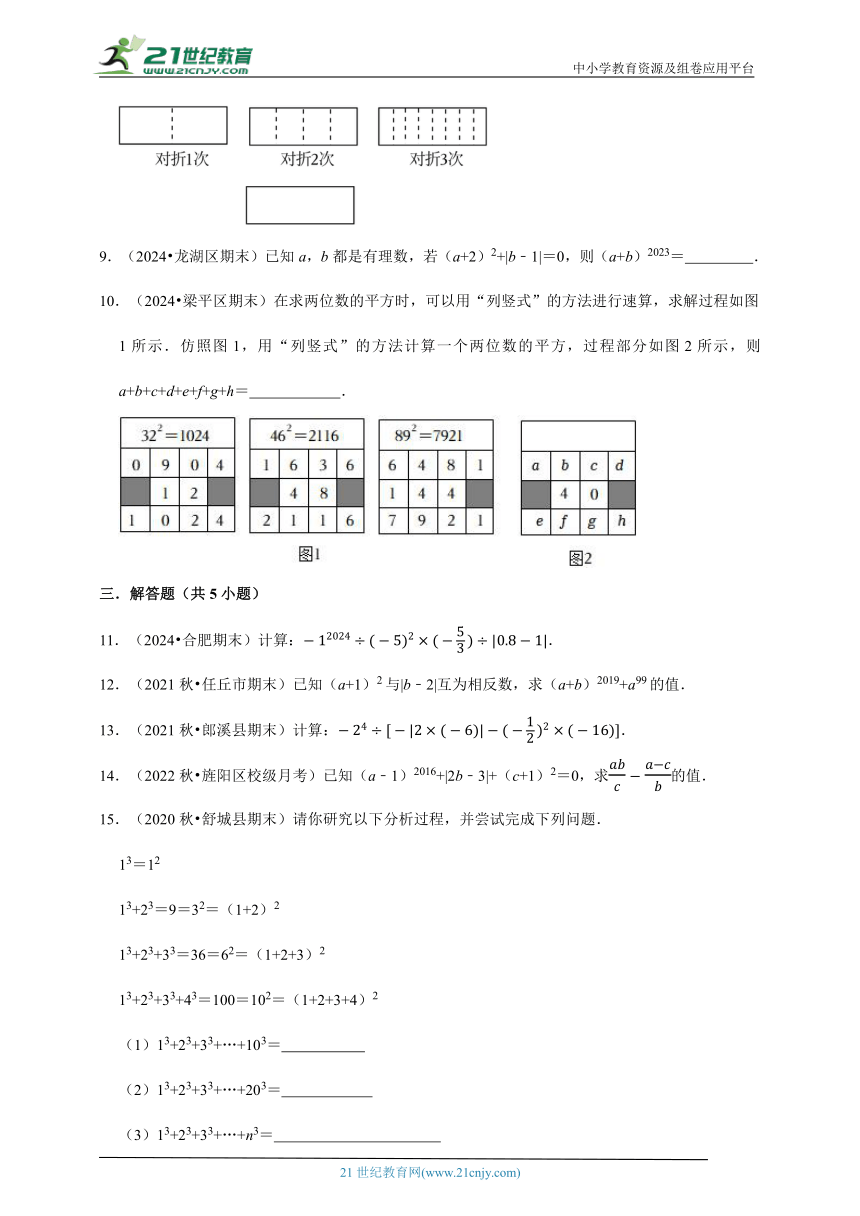
8.(2024 贵阳期末)将长方形纸片对折1次可得1条折痕,对折2次可得3条折痕,对折3次可得7条折痕,那么对折6次可得 条折痕.
9.(2024 龙湖区期末)已知a,b都是有理数,若(a+2)2+|b﹣1|=0,则(a+b)2023= .
10.(2024 梁平区期末)在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,过程部分如图2所示,则a+b+c+d+e+f+g+h= .
三.解答题(共5小题)
11.(2024 合肥期末)计算:.
12.(2021秋 任丘市期末)已知(a+1)2与|b﹣2|互为相反数,求(a+b)2019+a99的值.
13.(2021秋 郎溪县期末)计算:.
14.(2022秋 旌阳区校级月考)已知(a﹣1)2016+|2b﹣3|+(c+1)2=0,求的值.
15.(2020秋 舒城县期末)请你研究以下分析过程,并尝试完成下列问题.
13=12
13+23=9=32=(1+2)2
13+23+33=36=62=(1+2+3)2
13+23+33+43=100=102=(1+2+3+4)2
(1)13+23+33+…+103=
(2)13+23+33+…+203=
(3)13+23+33+…+n3=
(4)计算:113+123+133+…+203的值.
参考答案与试题解析
一.选择题(共5小题)
1.(2024 鼓楼区校级开学)池塘里的睡莲的面积每天长大一倍,若经过13天就可以长满整个池塘,则这些睡莲长满半个池塘需要( )天.
A.6 B.7 C.10 D.12
【考点】有理数的乘方.
【专题】实数;应用意识.
【答案】D
【分析】根据池塘里的睡莲的面积每天长大一倍的规律进行求解.
【解答】解:∵池塘里的睡莲的面积每天长大一倍,
∴长满整个池塘的前一天这些睡莲长满半个池塘,
13﹣1=12(天),
故选:D.
【点评】此题考查了有理数乘方运算的应用能力,关键是能准确根据题意进行求解.
2.(2024 宜兴市二模)若数a的平方等于16,那么数a可能是( )
A.2 B.﹣4 C.±4 D.±8
【考点】有理数的乘方.
【专题】实数;运算能力.
【答案】C
【分析】运用实数的平方运算进行求解.
【解答】解:∵(±4)2=16,
∴a=±4,
故选:C.
【点评】此题考查了实数平方运算的应用能力,关键是能准确理解并运用该知识进行计算.
3.(2024 邵阳期末)(﹣2)4的相反数是( )
A.﹣8 B.﹣16 C. D.8
【考点】有理数的乘方;相反数.
【答案】B
【分析】先计算有理数的乘方,再根据相反数的定义,即可解答.
【解答】解:(﹣2)4=16,16的相反数是﹣16,
故选:B.
【点评】本题考查了有理数的乘方、相反数,解决本题的关键是熟记有理数的乘方.
4.(2024 行唐县期末)下列可以表示7a的是( )
A. B.
C. D.
【考点】有理数的乘方.
【专题】计算题;运算能力.
【答案】D
【分析】根据有理数的乘方的概念进行选择即可.
【解答】解:7a表示a个7相乘,即个.
故选:D.
【点评】本题考查有理数的乘方,掌握有理数的乘方的概念是解题的关键.
5.(2024 淮北期末)下列各组数中,相等的一组是( )
A.﹣(﹣1)与﹣|﹣1| B.﹣32与(﹣3)2
C.(﹣4)3与﹣43 D.与()2
【考点】有理数的乘方;相反数;绝对值.
【答案】C
【分析】根据有理数的乘方的定义,绝对值的性质对各选项分别计算,然后利用排除法求解.
【解答】解:A、﹣|﹣1|=﹣1,﹣(﹣1)=1,﹣(﹣1)≠﹣|﹣1|,故本选项错误;
B、(﹣3)2=9,﹣32=﹣9,9≠﹣9,故本选项错误;
C、(﹣4)3=﹣64,﹣43=﹣64,(﹣4)3=﹣43,故本选项正确;
D、,,,故本选项错误.
故选:C.
【点评】本题考查了绝对值、有理数的乘方.解题的关键是掌握有理数的乘方运算法则,要注意﹣43与(﹣4)3的区别.
二.填空题(共5小题)
6.(2024春 松江区期中)如果a,b满足(a+3)2+|b﹣2|=0,那么ab= 9 .
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;运算能力.
【答案】9.
【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:∵(a+3)2+|b﹣2|=0,(a+3)2≥0,|b﹣2|≥0,
∴a+3=0,b﹣2=0,
解得a=﹣3,b=2,
∴ab=(﹣3)2=9.
故答案为:9.
【点评】本题考查平方数和绝对值的非负性,两个非负数的和为零,那么这两个非负数也为零是关键.
7.(2024 辉县市期末)有以下各式:①﹣|﹣2|;②﹣22;③(﹣3)2,其中负数有 2 个.
【考点】有理数的乘方;正数和负数;相反数;绝对值.
【专题】实数;运算能力.
【答案】2.
【分析】先利用有理数的乘方、相反数、绝对值逐个判定即可解答.
【解答】解:①﹣|﹣2|=﹣2是负数;②﹣22=﹣4是负数;③(﹣3)2=9是正数;其中计算结果为负数共2个.
故答案为:2.
【点评】本题主要考查了有理数的乘方、相反数、绝对值等知识点,掌握相关运算法则是解题的关键.
8.(2024 贵阳期末)将长方形纸片对折1次可得1条折痕,对折2次可得3条折痕,对折3次可得7条折痕,那么对折6次可得 63 条折痕.
【考点】有理数的乘方.
【专题】规律型;运算能力.
【答案】63.
【分析】对前三次对折分析不难发现每对折1次把纸分成的部分是上一次的2倍,折痕比所分成的部分数少1,求出第4次的折痕即可;再根据对折规律求出对折n次得到的部分数,然后减1即可得到折痕条数.
【解答】解:由图可知,第1次对折,把纸分成2部分,1条折痕,
第2次对折,把纸分成4部分,3条折痕,
第3次对折,把纸分成8部分,7条折痕,
…,
当n=6时,26﹣1=63,
故答案为:63.
【点评】本题是对图形变化规律的考查,观察得到对折得到的部分数与折痕的关系是解题的关键.
9.(2024 龙湖区期末)已知a,b都是有理数,若(a+2)2+|b﹣1|=0,则(a+b)2023= ﹣1 .
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;符号意识.
【答案】﹣1.
【分析】直接利用偶次方的性质以及绝对值的性质,进而得出a,b的值,即可得出答案.
【解答】解:∵(a+2)2+|b﹣1|=0,
∴a+2=0,b﹣1=0,
解得:a=﹣2,b=1,
故(a+b)2023=(﹣1)2023=﹣1.
故答案为:﹣1.
【点评】此题主要考查了非负数的性质,正确得出a,b的值是解题关键.
10.(2024 梁平区期末)在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,过程部分如图2所示,则a+b+c+d+e+f+g+h= 23或32 .
【考点】有理数的乘方.
【专题】规律型;数据分析观念.
【答案】23或32.
【分析】观察图象可知,第一行从右向左分别为个位数和十位数字的平方,每个数的平方占两个空,平方是一位数的前面的空用0填补,第二行从左边第2个空开始向右是这个两位数的两个数字的乘积的2倍,然后相加即为这个两位数的平方,根据此规律求解即可.
【解答】解:根据规律可知这个两位数为45或54,
当这个两位数为45时,a=1,b=6,c=2,d=5,e=2,f=0,g=2,h=5,则a+b+c+d+e+f+g+h=23,
当这个两位数为54时,a=2,b=5,c=1,d=6,e=2,f=9,g=1,h=6,则a+b+c+d+e+f+g+h=32,
故答案为:23或32.
【点评】本题是对数字变化规律的考查,仔细观察图形,观察出前两行的数与两位数的十位和个位上的数字的关系是解题的关键.
三.解答题(共5小题)
11.(2024 合肥期末)计算:.
【考点】有理数的乘方;绝对值;有理数的减法;有理数的乘法;有理数的除法.
【专题】实数;运算能力.
【答案】.
【分析】根据混合运算法则,先算乘方,再算绝对值符号里面的,最后算乘除即可.
【解答】解:原式
.
【点评】本题主要考查了实数的运算,解题关键是熟练掌握实数混合运算法则.
12.(2021秋 任丘市期末)已知(a+1)2与|b﹣2|互为相反数,求(a+b)2019+a99的值.
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;运算能力.
【答案】0.
【分析】根据互为相反数的两个数的和等于0,列出方程,再根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:∵(a+1)2与|b﹣2|互为相反数,
∴(a+1)2+|b﹣2|=0,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2,
∴(a+b)2019+a99=(﹣1+2)2019+(﹣1)99=1+(﹣1)=0,
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
13.(2021秋 郎溪县期末)计算:.
【考点】有理数的乘方;有理数的乘法.
【专题】计算题;符号意识;运算能力.
【答案】2.
【分析】根据乘方,绝对值的性质将其化简求解即可.
【解答】解:原式
=﹣16÷(﹣12+4)
=﹣16÷(﹣8)
=2.
【点评】本题考查了有理数的乘方和混合运算及绝对值的性质,关键在于熟记知识计算.
14.(2022秋 旌阳区校级月考)已知(a﹣1)2016+|2b﹣3|+(c+1)2=0,求的值.
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;运算能力.
【答案】.
【分析】根据非负数的性质列式求出a、b、c的值,然后代入代数式进行计算即可得解.
【解答】解:由非负数性质可得:a﹣1=0,2b﹣3=0,c+1=0,
解得:a=1,b,c=﹣1,
∴
.
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
15.(2020秋 舒城县期末)请你研究以下分析过程,并尝试完成下列问题.
13=12
13+23=9=32=(1+2)2
13+23+33=36=62=(1+2+3)2
13+23+33+43=100=102=(1+2+3+4)2
(1)13+23+33+…+103= 3025
(2)13+23+33+…+203= 44100
(3)13+23+33+…+n3=
(4)计算:113+123+133+…+203的值.
【考点】有理数的乘方.
【专题】规律型.
【答案】见试题解答内容
【分析】根据已知一系列等式,得出一般性规律,计算即可得到结果.
【解答】解:(1)13+23+33+…+103=3025;
(2)13+23+33+…+203=44100;
(3)13+23+33+…+n3;
(4)113+123+133+…+203=44100﹣3025=41075.
故答案为:(1)3025;(2)44100;(3);(4)41075.
【点评】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 有理数的乘方
一.选择题(共5小题)
1.(2024 鼓楼区校级开学)池塘里的睡莲的面积每天长大一倍,若经过13天就可以长满整个池塘,则这些睡莲长满半个池塘需要( )天.
A.6 B.7 C.10 D.12
2.(2024 宜兴市二模)若数a的平方等于16,那么数a可能是( )
A.2 B.﹣4 C.±4 D.±8
3.(2024 邵阳期末)(﹣2)4的相反数是( )
A.﹣8 B.﹣16 C. D.8
4.(2024 行唐县期末)下列可以表示7a的是( )
A. B.
C. D.
5.(2024 淮北期末)下列各组数中,相等的一组是( )
A.﹣(﹣1)与﹣|﹣1| B.﹣32与(﹣3)2
C.(﹣4)3与﹣43 D.与()2
二.填空题(共5小题)
6.(2024春 松江区期中)如果a,b满足(a+3)2+|b﹣2|=0,那么ab= .
7.(2024 辉县市期末)有以下各式:①﹣|﹣2|;②﹣22;③(﹣3)2,其中负数有 个.
8.(2024 贵阳期末)将长方形纸片对折1次可得1条折痕,对折2次可得3条折痕,对折3次可得7条折痕,那么对折6次可得 条折痕.
9.(2024 龙湖区期末)已知a,b都是有理数,若(a+2)2+|b﹣1|=0,则(a+b)2023= .
10.(2024 梁平区期末)在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,过程部分如图2所示,则a+b+c+d+e+f+g+h= .
三.解答题(共5小题)
11.(2024 合肥期末)计算:.
12.(2021秋 任丘市期末)已知(a+1)2与|b﹣2|互为相反数,求(a+b)2019+a99的值.
13.(2021秋 郎溪县期末)计算:.
14.(2022秋 旌阳区校级月考)已知(a﹣1)2016+|2b﹣3|+(c+1)2=0,求的值.
15.(2020秋 舒城县期末)请你研究以下分析过程,并尝试完成下列问题.
13=12
13+23=9=32=(1+2)2
13+23+33=36=62=(1+2+3)2
13+23+33+43=100=102=(1+2+3+4)2
(1)13+23+33+…+103=
(2)13+23+33+…+203=
(3)13+23+33+…+n3=
(4)计算:113+123+133+…+203的值.
参考答案与试题解析
一.选择题(共5小题)
1.(2024 鼓楼区校级开学)池塘里的睡莲的面积每天长大一倍,若经过13天就可以长满整个池塘,则这些睡莲长满半个池塘需要( )天.
A.6 B.7 C.10 D.12
【考点】有理数的乘方.
【专题】实数;应用意识.
【答案】D
【分析】根据池塘里的睡莲的面积每天长大一倍的规律进行求解.
【解答】解:∵池塘里的睡莲的面积每天长大一倍,
∴长满整个池塘的前一天这些睡莲长满半个池塘,
13﹣1=12(天),
故选:D.
【点评】此题考查了有理数乘方运算的应用能力,关键是能准确根据题意进行求解.
2.(2024 宜兴市二模)若数a的平方等于16,那么数a可能是( )
A.2 B.﹣4 C.±4 D.±8
【考点】有理数的乘方.
【专题】实数;运算能力.
【答案】C
【分析】运用实数的平方运算进行求解.
【解答】解:∵(±4)2=16,
∴a=±4,
故选:C.
【点评】此题考查了实数平方运算的应用能力,关键是能准确理解并运用该知识进行计算.
3.(2024 邵阳期末)(﹣2)4的相反数是( )
A.﹣8 B.﹣16 C. D.8
【考点】有理数的乘方;相反数.
【答案】B
【分析】先计算有理数的乘方,再根据相反数的定义,即可解答.
【解答】解:(﹣2)4=16,16的相反数是﹣16,
故选:B.
【点评】本题考查了有理数的乘方、相反数,解决本题的关键是熟记有理数的乘方.
4.(2024 行唐县期末)下列可以表示7a的是( )
A. B.
C. D.
【考点】有理数的乘方.
【专题】计算题;运算能力.
【答案】D
【分析】根据有理数的乘方的概念进行选择即可.
【解答】解:7a表示a个7相乘,即个.
故选:D.
【点评】本题考查有理数的乘方,掌握有理数的乘方的概念是解题的关键.
5.(2024 淮北期末)下列各组数中,相等的一组是( )
A.﹣(﹣1)与﹣|﹣1| B.﹣32与(﹣3)2
C.(﹣4)3与﹣43 D.与()2
【考点】有理数的乘方;相反数;绝对值.
【答案】C
【分析】根据有理数的乘方的定义,绝对值的性质对各选项分别计算,然后利用排除法求解.
【解答】解:A、﹣|﹣1|=﹣1,﹣(﹣1)=1,﹣(﹣1)≠﹣|﹣1|,故本选项错误;
B、(﹣3)2=9,﹣32=﹣9,9≠﹣9,故本选项错误;
C、(﹣4)3=﹣64,﹣43=﹣64,(﹣4)3=﹣43,故本选项正确;
D、,,,故本选项错误.
故选:C.
【点评】本题考查了绝对值、有理数的乘方.解题的关键是掌握有理数的乘方运算法则,要注意﹣43与(﹣4)3的区别.
二.填空题(共5小题)
6.(2024春 松江区期中)如果a,b满足(a+3)2+|b﹣2|=0,那么ab= 9 .
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;运算能力.
【答案】9.
【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:∵(a+3)2+|b﹣2|=0,(a+3)2≥0,|b﹣2|≥0,
∴a+3=0,b﹣2=0,
解得a=﹣3,b=2,
∴ab=(﹣3)2=9.
故答案为:9.
【点评】本题考查平方数和绝对值的非负性,两个非负数的和为零,那么这两个非负数也为零是关键.
7.(2024 辉县市期末)有以下各式:①﹣|﹣2|;②﹣22;③(﹣3)2,其中负数有 2 个.
【考点】有理数的乘方;正数和负数;相反数;绝对值.
【专题】实数;运算能力.
【答案】2.
【分析】先利用有理数的乘方、相反数、绝对值逐个判定即可解答.
【解答】解:①﹣|﹣2|=﹣2是负数;②﹣22=﹣4是负数;③(﹣3)2=9是正数;其中计算结果为负数共2个.
故答案为:2.
【点评】本题主要考查了有理数的乘方、相反数、绝对值等知识点,掌握相关运算法则是解题的关键.
8.(2024 贵阳期末)将长方形纸片对折1次可得1条折痕,对折2次可得3条折痕,对折3次可得7条折痕,那么对折6次可得 63 条折痕.
【考点】有理数的乘方.
【专题】规律型;运算能力.
【答案】63.
【分析】对前三次对折分析不难发现每对折1次把纸分成的部分是上一次的2倍,折痕比所分成的部分数少1,求出第4次的折痕即可;再根据对折规律求出对折n次得到的部分数,然后减1即可得到折痕条数.
【解答】解:由图可知,第1次对折,把纸分成2部分,1条折痕,
第2次对折,把纸分成4部分,3条折痕,
第3次对折,把纸分成8部分,7条折痕,
…,
当n=6时,26﹣1=63,
故答案为:63.
【点评】本题是对图形变化规律的考查,观察得到对折得到的部分数与折痕的关系是解题的关键.
9.(2024 龙湖区期末)已知a,b都是有理数,若(a+2)2+|b﹣1|=0,则(a+b)2023= ﹣1 .
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;符号意识.
【答案】﹣1.
【分析】直接利用偶次方的性质以及绝对值的性质,进而得出a,b的值,即可得出答案.
【解答】解:∵(a+2)2+|b﹣1|=0,
∴a+2=0,b﹣1=0,
解得:a=﹣2,b=1,
故(a+b)2023=(﹣1)2023=﹣1.
故答案为:﹣1.
【点评】此题主要考查了非负数的性质,正确得出a,b的值是解题关键.
10.(2024 梁平区期末)在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,过程部分如图2所示,则a+b+c+d+e+f+g+h= 23或32 .
【考点】有理数的乘方.
【专题】规律型;数据分析观念.
【答案】23或32.
【分析】观察图象可知,第一行从右向左分别为个位数和十位数字的平方,每个数的平方占两个空,平方是一位数的前面的空用0填补,第二行从左边第2个空开始向右是这个两位数的两个数字的乘积的2倍,然后相加即为这个两位数的平方,根据此规律求解即可.
【解答】解:根据规律可知这个两位数为45或54,
当这个两位数为45时,a=1,b=6,c=2,d=5,e=2,f=0,g=2,h=5,则a+b+c+d+e+f+g+h=23,
当这个两位数为54时,a=2,b=5,c=1,d=6,e=2,f=9,g=1,h=6,则a+b+c+d+e+f+g+h=32,
故答案为:23或32.
【点评】本题是对数字变化规律的考查,仔细观察图形,观察出前两行的数与两位数的十位和个位上的数字的关系是解题的关键.
三.解答题(共5小题)
11.(2024 合肥期末)计算:.
【考点】有理数的乘方;绝对值;有理数的减法;有理数的乘法;有理数的除法.
【专题】实数;运算能力.
【答案】.
【分析】根据混合运算法则,先算乘方,再算绝对值符号里面的,最后算乘除即可.
【解答】解:原式
.
【点评】本题主要考查了实数的运算,解题关键是熟练掌握实数混合运算法则.
12.(2021秋 任丘市期末)已知(a+1)2与|b﹣2|互为相反数,求(a+b)2019+a99的值.
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;运算能力.
【答案】0.
【分析】根据互为相反数的两个数的和等于0,列出方程,再根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:∵(a+1)2与|b﹣2|互为相反数,
∴(a+1)2+|b﹣2|=0,
∴a+1=0,b﹣2=0,
∴a=﹣1,b=2,
∴(a+b)2019+a99=(﹣1+2)2019+(﹣1)99=1+(﹣1)=0,
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
13.(2021秋 郎溪县期末)计算:.
【考点】有理数的乘方;有理数的乘法.
【专题】计算题;符号意识;运算能力.
【答案】2.
【分析】根据乘方,绝对值的性质将其化简求解即可.
【解答】解:原式
=﹣16÷(﹣12+4)
=﹣16÷(﹣8)
=2.
【点评】本题考查了有理数的乘方和混合运算及绝对值的性质,关键在于熟记知识计算.
14.(2022秋 旌阳区校级月考)已知(a﹣1)2016+|2b﹣3|+(c+1)2=0,求的值.
【考点】非负数的性质:偶次方;非负数的性质:绝对值.
【专题】实数;运算能力.
【答案】.
【分析】根据非负数的性质列式求出a、b、c的值,然后代入代数式进行计算即可得解.
【解答】解:由非负数性质可得:a﹣1=0,2b﹣3=0,c+1=0,
解得:a=1,b,c=﹣1,
∴
.
【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
15.(2020秋 舒城县期末)请你研究以下分析过程,并尝试完成下列问题.
13=12
13+23=9=32=(1+2)2
13+23+33=36=62=(1+2+3)2
13+23+33+43=100=102=(1+2+3+4)2
(1)13+23+33+…+103= 3025
(2)13+23+33+…+203= 44100
(3)13+23+33+…+n3=
(4)计算:113+123+133+…+203的值.
【考点】有理数的乘方.
【专题】规律型.
【答案】见试题解答内容
【分析】根据已知一系列等式,得出一般性规律,计算即可得到结果.
【解答】解:(1)13+23+33+…+103=3025;
(2)13+23+33+…+203=44100;
(3)13+23+33+…+n3;
(4)113+123+133+…+203=44100﹣3025=41075.
故答案为:(1)3025;(2)44100;(3);(4)41075.
【点评】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
