12.2三角形全等的判定(预习衔接.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 12.2三角形全等的判定(预习衔接.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 16:21:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
新课预习衔接 三角形全等的判定
一.选择题(共5小题)
1.(2024 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
2.(2024 民权县期末)如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
3.(2024 江门期末)如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
4.(2024春 济宁期末)如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=6,AC=8,则BD长( )
A.12 B.14 C.16 D.18
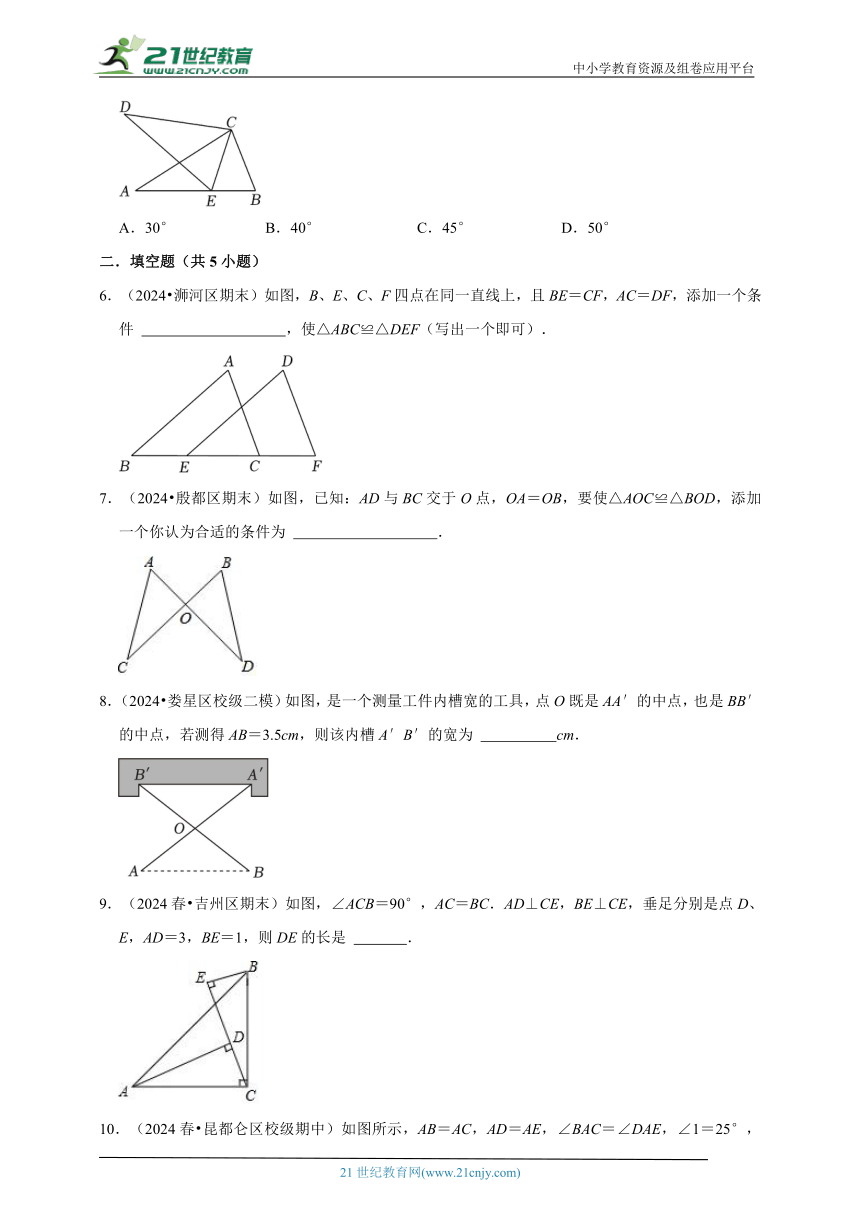
5.(2024 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
二.填空题(共5小题)
6.(2024 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 ,使△ABC≌△DEF(写出一个即可).
7.(2024 殷都区期末)如图,已知:AD与BC交于O点,OA=OB,要使△AOC≌△BOD,添加一个你认为合适的条件为 .
8.(2024 娄星区校级二模)如图,是一个测量工件内槽宽的工具,点O既是AA′的中点,也是BB′的中点,若测得AB=3.5cm,则该内槽A′B′的宽为 cm.
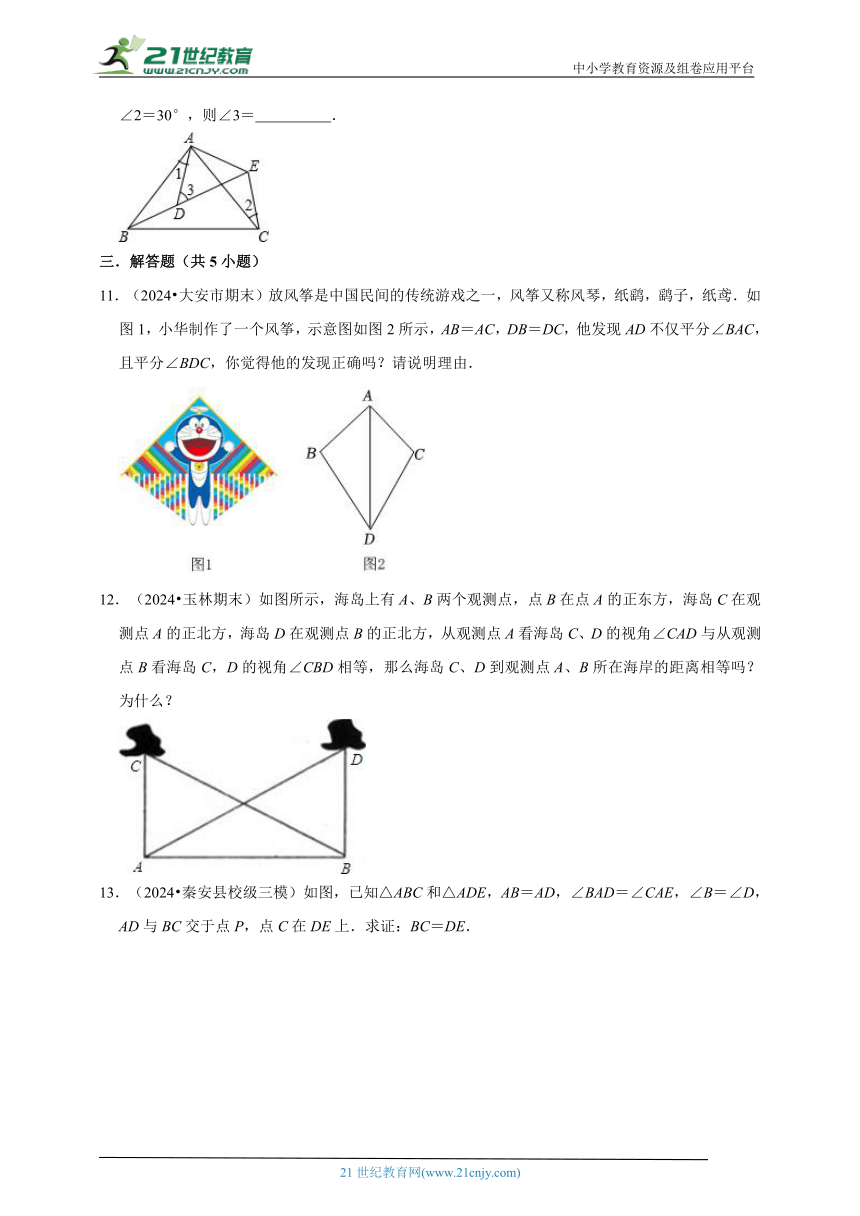
9.(2024春 吉州区期末)如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是 .
10.(2024春 昆都仑区校级期中)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
三.解答题(共5小题)
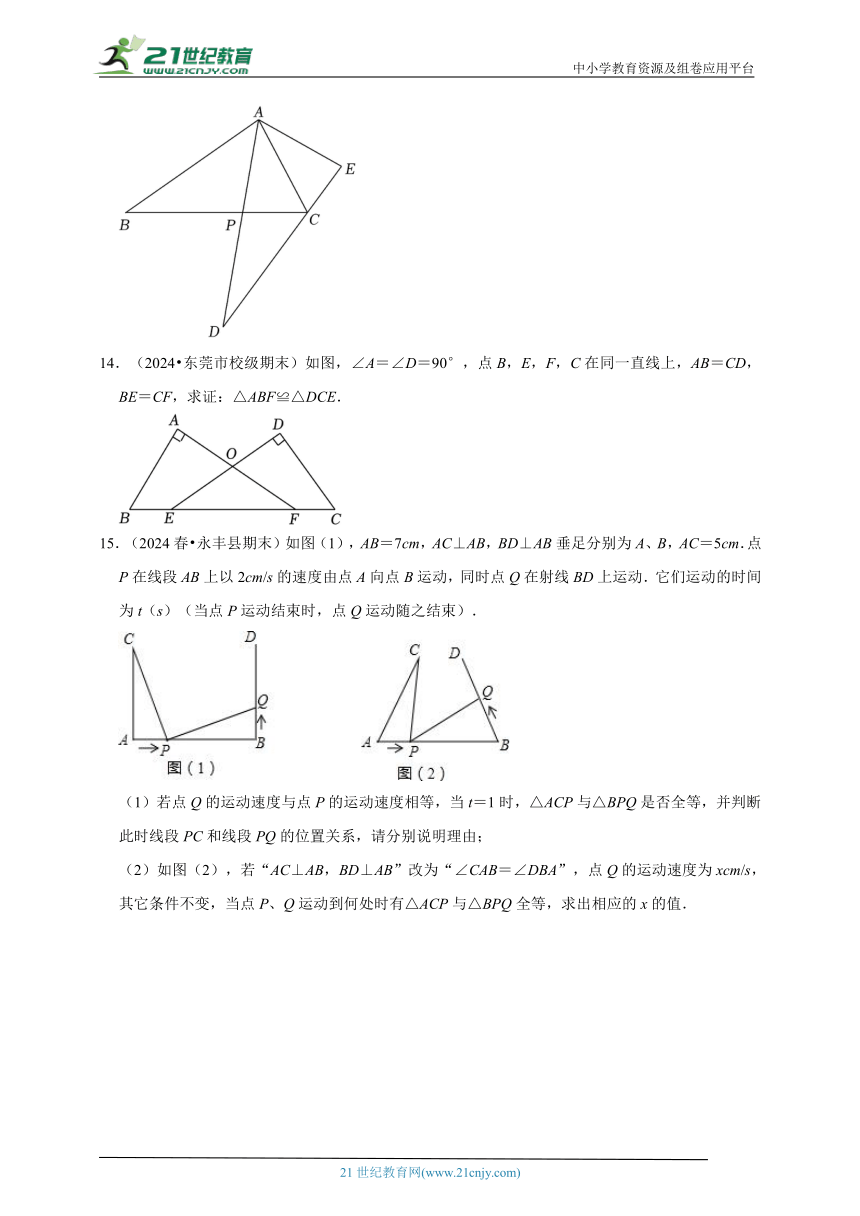
11.(2024 大安市期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,AB=AC,DB=DC,他发现AD不仅平分∠BAC,且平分∠BDC,你觉得他的发现正确吗?请说明理由.
12.(2024 玉林期末)如图所示,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C、D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
13.(2024 秦安县校级三模)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.求证:BC=DE.
14.(2024 东莞市校级期末)如图,∠A=∠D=90°,点B,E,F,C在同一直线上,AB=CD,BE=CF,求证:△ABF≌△DCE.
15.(2024春 永丰县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点Q的运动速度为xcm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等,求出相应的x的值.
新课预习衔接 三角形全等的判定
参考答案与试题解析
一.选择题(共5小题)
1.(2024 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】C
【分析】根据三角形全等的判定方法即可求解.
【解答】解:在△EFG与△NMH中,已知,∠E=∠N,EF=NM,
A.由EH=NG可得EG=NH,所以添加条件EH=NG,根据SAS可证△EFG≌△NMH,故本选项不符合题意;
B.添加条件∠F=∠M,根据ASA可证△EFG≌△NMH,故本选项不符合题意;
C.添加条件FG=MH,不能证明△EFG≌△NMH,故本选项符合题意;
D.由FG∥HM可得∠EGF=∠NHM,所以添加条件FG∥HM,根据AAS可证△EFG≌△NMH,故本选项不符合题意;
故选:C.
【点评】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是难度适中.
2.(2024 民权县期末)如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
【考点】直角三角形全等的判定;三角形内角和定理.
【专题】计算题.
【答案】B
【分析】根据∠C=90°,AD=AC,且AE=AE,求证△CAE≌△DAE(HL),∠CAE=∠DAE∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.
【解答】解:在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,且AE=AE,
∴△CAE≌△DAE(HL),
∴∠CAE=∠DAE∠CAB,
∵∠B+∠CAB=90°,∠B=28°,
∴∠CAB=90°﹣28°=62°,
∴∠AEC=90°∠CAB=90°﹣31°=59°.
故选:B.
【点评】此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握,解答此题的关键是求证△CAE≌△DAE,此题稍微有点难度,属于中档题.
3.(2024 江门期末)如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
【考点】全等三角形的应用.
【答案】C
【分析】此题可以采用排除法进行分析从而确定最后的答案.
【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
【点评】此题主要考查学生对全等三角形的判定方法的灵活运用,要求对常用的几种方法熟练掌握.
4.(2024春 济宁期末)如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=6,AC=8,则BD长( )
A.12 B.14 C.16 D.18
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形对应边相等得到BC=CE=6,CD=AC=8,则BD=BC+CD=14.
【解答】解:∵△ABC≌△DEC,
∴BC=CE=6,CD=AC=8,
∴BD=BC+CD=14,
故选:B.
【点评】本题主要考查了全等三角形的性质,熟记全等三角形的性质是解题的关键.
5.(2024 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】B
【分析】由全等三角形的性质推出BC=CE,∠DCE=∠ACB,由等腰三角形的性质得到∠CEB=∠B=70°,求出∠ECB=180°﹣∠CEB﹣∠B=40°,又∠ACD+∠ACE=∠ECB+∠ACE,即可得到∠ACD=∠ECB=40°.
【解答】解:∵△ABC≌△DEC,
∴BC=CE,∠DCE=∠ACB,
∴∠CEB=∠B=70°,
∴∠ECB=180°﹣∠CEB﹣∠B=40°,
∵∠ACD+∠ACE=∠ECB+∠ACE,
∴∠ACD=∠ECB=40°.
故选:B.
【点评】本题考查全等三角形的性质,等腰三角形的性质,关键是由△ABC≌△DEC,得到BC=CE,∠DCE=∠ACB.
二.填空题(共5小题)
6.(2024 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 AB=DE(答案不唯一) ,使△ABC≌△DEF(写出一个即可).
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】AB=DE(答案不唯一).
【分析】根据全等三角形的判定添加合适的条件即可.
【解答】解:添加AB=DE(答案不唯一),
证明如下:∵BE=CF,
∴BE+EC=CF+EC,
即BC=FE,
∵AC=DF,AB=DE,
∴△ABC≌△DEF(SSS),
故答案为:AB=DE(答案不唯一).
【点评】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.
7.(2024 殷都区期末)如图,已知:AD与BC交于O点,OA=OB,要使△AOC≌△BOD,添加一个你认为合适的条件为 OC=OD(答案不唯一) .
【考点】全等三角形的判定.
【专题】证明题;图形的全等;推理能力.
【答案】OC=OD(答案不唯一).
【分析】此题答案不唯一,可以是OC=OD,根据全等三角形的判定定理SAS可证出来.
【解答】解:OC=OD,
理由是:∵在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
故答案为:OC=OD(答案不唯一).
【点评】本题考查了全等三角形的判定定理的应用,此题是一道开放型的题目,答案不唯一,还可以∠C=∠D或∠A=∠B.
8.(2024 娄星区校级二模)如图,是一个测量工件内槽宽的工具,点O既是AA′的中点,也是BB′的中点,若测得AB=3.5cm,则该内槽A′B′的宽为 3.5 cm.
【考点】全等三角形的应用.
【专题】图形的全等;运算能力.
【答案】3.5.
【分析】利用SAS证明△AOB≌△A′OB′,即可解答.
【解答】解:∵点O既是AA′的中点,也是BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS),
∴AB=A′B′=3.5cm,
故答案为:3.5.
【点评】本题考查了全等三角形的应用,解题的关键是熟练掌握全等三角的判定法方法.
9.(2024春 吉州区期末)如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是 2 .
【考点】全等三角形的判定与性质.
【专题】三角形.
【答案】见试题解答内容
【分析】根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC,就可以得出BE=DC,就可以求出DE的值.
【解答】解:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
,
∴△CEB≌△ADC(AAS),
∴BE=DC=1,CE=AD=3.
∴DE=EC﹣CD=3﹣1=2
故选答案为2.
【点评】本题考查全等三角形的判定和性质、熟练掌握全等三角形的判定和性质是解决问题的关键,学会正确寻找全等三角形,属于中考常考题型.
10.(2024春 昆都仑区校级期中)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= 55° .
【考点】全等三角形的判定与性质.
【答案】见试题解答内容
【分析】求出∠BAD=∠EAC,证△BAD≌△CAE,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解答】解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
【点评】本题考查了全等三角形的性质和判定,三角形的外角性质的应用,解此题的关键是推出△BAD≌△CAE.
三.解答题(共5小题)
11.(2024 大安市期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,AB=AC,DB=DC,他发现AD不仅平分∠BAC,且平分∠BDC,你觉得他的发现正确吗?请说明理由.
【考点】全等三角形的判定与性质.
【专题】证明题;应用意识.
【答案】见试题解答内容
【分析】利用SSS证明△ABD≌△ACD即可解决问题.
【解答】解:结论正确.
证明如下:
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠BDA=∠CDA,
即AD不仅平分∠BAC,且平分∠BDC,
∴结论正确.
【点评】此题主要考查了全等三角形的性质与判定,比较简单.
12.(2024 玉林期末)如图所示,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C、D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
【考点】全等三角形的应用.
【专题】应用题.
【答案】见试题解答内容
【分析】由方位可以得出∠CAB=∠DBA,而已知视角∠CAD=视角∠CBD,公共边AB=BA,容易得出△ABC≌△BAD,所以AC=BD.
【解答】解:相等.
理由:
∵∠CAD=∠CBD,∠COA=∠DOB(对顶角),
∴由内角和定理,得∠C=∠D,
又∵∠CAB=∠DBA=90°,
在△CAB和△DBA中,
∴△CAB≌△DBA(AAS),
∴CA=DB,
∴海岛C、D到观测点A、B所在海岸的距离相等.
【点评】本题考查了全等三角形的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.关键是证明△ABC≌△BAD,从而求得AC=BD.
13.(2024 秦安县校级三模)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.求证:BC=DE.
【考点】全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】证明见解析.
【分析】先证∠BAC=∠DAE,再证△ABC≌△ADE(ASA),即可得出结论.
【解答】证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA),
∴BC=DE.
【点评】本题考查了全等三角形的判定与性质,证明△ABC≌△ADE是解题的关键.
14.(2024 东莞市校级期末)如图,∠A=∠D=90°,点B,E,F,C在同一直线上,AB=CD,BE=CF,求证:△ABF≌△DCE.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】见解析.
【分析】先证出BF=CE,由HL证明Rt△ABF≌Rt△DCE即可.
【解答】证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
∵∠A=∠D=90°,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL),
【点评】本题考查了全等三角形的判定与性质,解题的关键是掌握全等三角形的判定方法.
15.(2024春 永丰县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点Q的运动速度为xcm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等,求出相应的x的值.
【考点】全等三角形的判定.
【专题】三角形;应用意识.
【答案】见试题解答内容
【分析】(1)利用AP=BQ=2,BP=AC,可根据“SAS”证明△ACP≌△BPQ;则∠C=∠BPQ,然后证明∠APC+∠BPQ=90°,从而得到PC⊥PQ;
(2)讨论:若△ACP≌△BPQ,则AC=BP,AP=BQ,即5=7﹣2t,2t=xt;②若△ACP≌△BQP,则AC=BQ,AP=BP,即5=xt,2t=7﹣2t,然后分别求出x即可.
【解答】解:(1)△ACP≌△BPQ,PC⊥PQ.
理由如下:∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
在△ACP和△BPQ中
,
∴△ACP≌△BPQ(SAS);
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t
解得:x,t.
综上所述,当△ACP与△BPQ全等时x的值为2或.
【点评】本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 三角形全等的判定
一.选择题(共5小题)
1.(2024 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
2.(2024 民权县期末)如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
3.(2024 江门期末)如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
4.(2024春 济宁期末)如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=6,AC=8,则BD长( )
A.12 B.14 C.16 D.18
5.(2024 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
二.填空题(共5小题)
6.(2024 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 ,使△ABC≌△DEF(写出一个即可).
7.(2024 殷都区期末)如图,已知:AD与BC交于O点,OA=OB,要使△AOC≌△BOD,添加一个你认为合适的条件为 .
8.(2024 娄星区校级二模)如图,是一个测量工件内槽宽的工具,点O既是AA′的中点,也是BB′的中点,若测得AB=3.5cm,则该内槽A′B′的宽为 cm.
9.(2024春 吉州区期末)如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是 .
10.(2024春 昆都仑区校级期中)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
三.解答题(共5小题)
11.(2024 大安市期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,AB=AC,DB=DC,他发现AD不仅平分∠BAC,且平分∠BDC,你觉得他的发现正确吗?请说明理由.
12.(2024 玉林期末)如图所示,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C、D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
13.(2024 秦安县校级三模)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.求证:BC=DE.
14.(2024 东莞市校级期末)如图,∠A=∠D=90°,点B,E,F,C在同一直线上,AB=CD,BE=CF,求证:△ABF≌△DCE.
15.(2024春 永丰县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点Q的运动速度为xcm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等,求出相应的x的值.
新课预习衔接 三角形全等的判定
参考答案与试题解析
一.选择题(共5小题)
1.(2024 全椒县期末)如图,点E、H、G、N共线,∠E=∠N,EF=NM,添加一个条件,不能判断△EFG≌△NMH的是( )
A.EH=NG B.∠F=∠M C.FG=MH D.FG∥HM
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】C
【分析】根据三角形全等的判定方法即可求解.
【解答】解:在△EFG与△NMH中,已知,∠E=∠N,EF=NM,
A.由EH=NG可得EG=NH,所以添加条件EH=NG,根据SAS可证△EFG≌△NMH,故本选项不符合题意;
B.添加条件∠F=∠M,根据ASA可证△EFG≌△NMH,故本选项不符合题意;
C.添加条件FG=MH,不能证明△EFG≌△NMH,故本选项符合题意;
D.由FG∥HM可得∠EGF=∠NHM,所以添加条件FG∥HM,根据AAS可证△EFG≌△NMH,故本选项不符合题意;
故选:C.
【点评】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是难度适中.
2.(2024 民权县期末)如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
【考点】直角三角形全等的判定;三角形内角和定理.
【专题】计算题.
【答案】B
【分析】根据∠C=90°,AD=AC,且AE=AE,求证△CAE≌△DAE(HL),∠CAE=∠DAE∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.
【解答】解:在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,且AE=AE,
∴△CAE≌△DAE(HL),
∴∠CAE=∠DAE∠CAB,
∵∠B+∠CAB=90°,∠B=28°,
∴∠CAB=90°﹣28°=62°,
∴∠AEC=90°∠CAB=90°﹣31°=59°.
故选:B.
【点评】此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握,解答此题的关键是求证△CAE≌△DAE,此题稍微有点难度,属于中档题.
3.(2024 江门期末)如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A.① B.② C.③ D.①和②
【考点】全等三角形的应用.
【答案】C
【分析】此题可以采用排除法进行分析从而确定最后的答案.
【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
【点评】此题主要考查学生对全等三角形的判定方法的灵活运用,要求对常用的几种方法熟练掌握.
4.(2024春 济宁期末)如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=6,AC=8,则BD长( )
A.12 B.14 C.16 D.18
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形对应边相等得到BC=CE=6,CD=AC=8,则BD=BC+CD=14.
【解答】解:∵△ABC≌△DEC,
∴BC=CE=6,CD=AC=8,
∴BD=BC+CD=14,
故选:B.
【点评】本题主要考查了全等三角形的性质,熟记全等三角形的性质是解题的关键.
5.(2024 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】B
【分析】由全等三角形的性质推出BC=CE,∠DCE=∠ACB,由等腰三角形的性质得到∠CEB=∠B=70°,求出∠ECB=180°﹣∠CEB﹣∠B=40°,又∠ACD+∠ACE=∠ECB+∠ACE,即可得到∠ACD=∠ECB=40°.
【解答】解:∵△ABC≌△DEC,
∴BC=CE,∠DCE=∠ACB,
∴∠CEB=∠B=70°,
∴∠ECB=180°﹣∠CEB﹣∠B=40°,
∵∠ACD+∠ACE=∠ECB+∠ACE,
∴∠ACD=∠ECB=40°.
故选:B.
【点评】本题考查全等三角形的性质,等腰三角形的性质,关键是由△ABC≌△DEC,得到BC=CE,∠DCE=∠ACB.
二.填空题(共5小题)
6.(2024 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 AB=DE(答案不唯一) ,使△ABC≌△DEF(写出一个即可).
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】AB=DE(答案不唯一).
【分析】根据全等三角形的判定添加合适的条件即可.
【解答】解:添加AB=DE(答案不唯一),
证明如下:∵BE=CF,
∴BE+EC=CF+EC,
即BC=FE,
∵AC=DF,AB=DE,
∴△ABC≌△DEF(SSS),
故答案为:AB=DE(答案不唯一).
【点评】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.
7.(2024 殷都区期末)如图,已知:AD与BC交于O点,OA=OB,要使△AOC≌△BOD,添加一个你认为合适的条件为 OC=OD(答案不唯一) .
【考点】全等三角形的判定.
【专题】证明题;图形的全等;推理能力.
【答案】OC=OD(答案不唯一).
【分析】此题答案不唯一,可以是OC=OD,根据全等三角形的判定定理SAS可证出来.
【解答】解:OC=OD,
理由是:∵在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
故答案为:OC=OD(答案不唯一).
【点评】本题考查了全等三角形的判定定理的应用,此题是一道开放型的题目,答案不唯一,还可以∠C=∠D或∠A=∠B.
8.(2024 娄星区校级二模)如图,是一个测量工件内槽宽的工具,点O既是AA′的中点,也是BB′的中点,若测得AB=3.5cm,则该内槽A′B′的宽为 3.5 cm.
【考点】全等三角形的应用.
【专题】图形的全等;运算能力.
【答案】3.5.
【分析】利用SAS证明△AOB≌△A′OB′,即可解答.
【解答】解:∵点O既是AA′的中点,也是BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS),
∴AB=A′B′=3.5cm,
故答案为:3.5.
【点评】本题考查了全等三角形的应用,解题的关键是熟练掌握全等三角的判定法方法.
9.(2024春 吉州区期末)如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是 2 .
【考点】全等三角形的判定与性质.
【专题】三角形.
【答案】见试题解答内容
【分析】根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC,就可以得出BE=DC,就可以求出DE的值.
【解答】解:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
,
∴△CEB≌△ADC(AAS),
∴BE=DC=1,CE=AD=3.
∴DE=EC﹣CD=3﹣1=2
故选答案为2.
【点评】本题考查全等三角形的判定和性质、熟练掌握全等三角形的判定和性质是解决问题的关键,学会正确寻找全等三角形,属于中考常考题型.
10.(2024春 昆都仑区校级期中)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= 55° .
【考点】全等三角形的判定与性质.
【答案】见试题解答内容
【分析】求出∠BAD=∠EAC,证△BAD≌△CAE,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解答】解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
【点评】本题考查了全等三角形的性质和判定,三角形的外角性质的应用,解此题的关键是推出△BAD≌△CAE.
三.解答题(共5小题)
11.(2024 大安市期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,AB=AC,DB=DC,他发现AD不仅平分∠BAC,且平分∠BDC,你觉得他的发现正确吗?请说明理由.
【考点】全等三角形的判定与性质.
【专题】证明题;应用意识.
【答案】见试题解答内容
【分析】利用SSS证明△ABD≌△ACD即可解决问题.
【解答】解:结论正确.
证明如下:
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠BDA=∠CDA,
即AD不仅平分∠BAC,且平分∠BDC,
∴结论正确.
【点评】此题主要考查了全等三角形的性质与判定,比较简单.
12.(2024 玉林期末)如图所示,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C、D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
【考点】全等三角形的应用.
【专题】应用题.
【答案】见试题解答内容
【分析】由方位可以得出∠CAB=∠DBA,而已知视角∠CAD=视角∠CBD,公共边AB=BA,容易得出△ABC≌△BAD,所以AC=BD.
【解答】解:相等.
理由:
∵∠CAD=∠CBD,∠COA=∠DOB(对顶角),
∴由内角和定理,得∠C=∠D,
又∵∠CAB=∠DBA=90°,
在△CAB和△DBA中,
∴△CAB≌△DBA(AAS),
∴CA=DB,
∴海岛C、D到观测点A、B所在海岸的距离相等.
【点评】本题考查了全等三角形的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.关键是证明△ABC≌△BAD,从而求得AC=BD.
13.(2024 秦安县校级三模)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.求证:BC=DE.
【考点】全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】证明见解析.
【分析】先证∠BAC=∠DAE,再证△ABC≌△ADE(ASA),即可得出结论.
【解答】证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA),
∴BC=DE.
【点评】本题考查了全等三角形的判定与性质,证明△ABC≌△ADE是解题的关键.
14.(2024 东莞市校级期末)如图,∠A=∠D=90°,点B,E,F,C在同一直线上,AB=CD,BE=CF,求证:△ABF≌△DCE.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】见解析.
【分析】先证出BF=CE,由HL证明Rt△ABF≌Rt△DCE即可.
【解答】证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
∵∠A=∠D=90°,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL),
【点评】本题考查了全等三角形的判定与性质,解题的关键是掌握全等三角形的判定方法.
15.(2024春 永丰县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P在线段AB上以2cm/s的速度由点A向点B运动,同时点Q在射线BD上运动.它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;
(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,点Q的运动速度为xcm/s,其它条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等,求出相应的x的值.
【考点】全等三角形的判定.
【专题】三角形;应用意识.
【答案】见试题解答内容
【分析】(1)利用AP=BQ=2,BP=AC,可根据“SAS”证明△ACP≌△BPQ;则∠C=∠BPQ,然后证明∠APC+∠BPQ=90°,从而得到PC⊥PQ;
(2)讨论:若△ACP≌△BPQ,则AC=BP,AP=BQ,即5=7﹣2t,2t=xt;②若△ACP≌△BQP,则AC=BQ,AP=BP,即5=xt,2t=7﹣2t,然后分别求出x即可.
【解答】解:(1)△ACP≌△BPQ,PC⊥PQ.
理由如下:∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
在△ACP和△BPQ中
,
∴△ACP≌△BPQ(SAS);
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t
解得:x,t.
综上所述,当△ACP与△BPQ全等时x的值为2或.
【点评】本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
