23.3相似三角形(预习衔接.含解析)-2025-2026学年九年级上册数学华东师大版
文档属性
| 名称 | 23.3相似三角形(预习衔接.含解析)-2025-2026学年九年级上册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 226.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 16:08:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新课预习衔接 相似三角形
一.选择题(共5小题)
1.(2024 合水县一模)若△ABC∽△DEF,S△ABC:S△DEF=2:3,则△ABC与△DEF的相似比为( )
A.2:3 B.4:9 C. D.3:2
2.(2024 洪山区校级二模)如图,在平行四边形ABCD中,点E在边AB上,连接DE,交对角线AC于点F,如果,CD=6,那么BE的值为( )
A.2 B.3 C.4 D.5
3.(2024 昭阳区一模)如图,D,E是△ABC边AB,AC边上的两点,且DE∥BC,若S△ADE:S△ABC=1:16,则△ADE与△ABC的周长之比为( )
A.1:2 B.1:4 C.1:5 D.1:16
4.(2024 沭阳县校级月考)如图,已知∠1=∠2,那么添加下列的一个条件后,仍无法判定△ABC∽△ADE的是( )
A. B.∠B=∠D C. D.∠C=∠AED
5.(2024 济南三模)如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
二.填空题(共5小题)
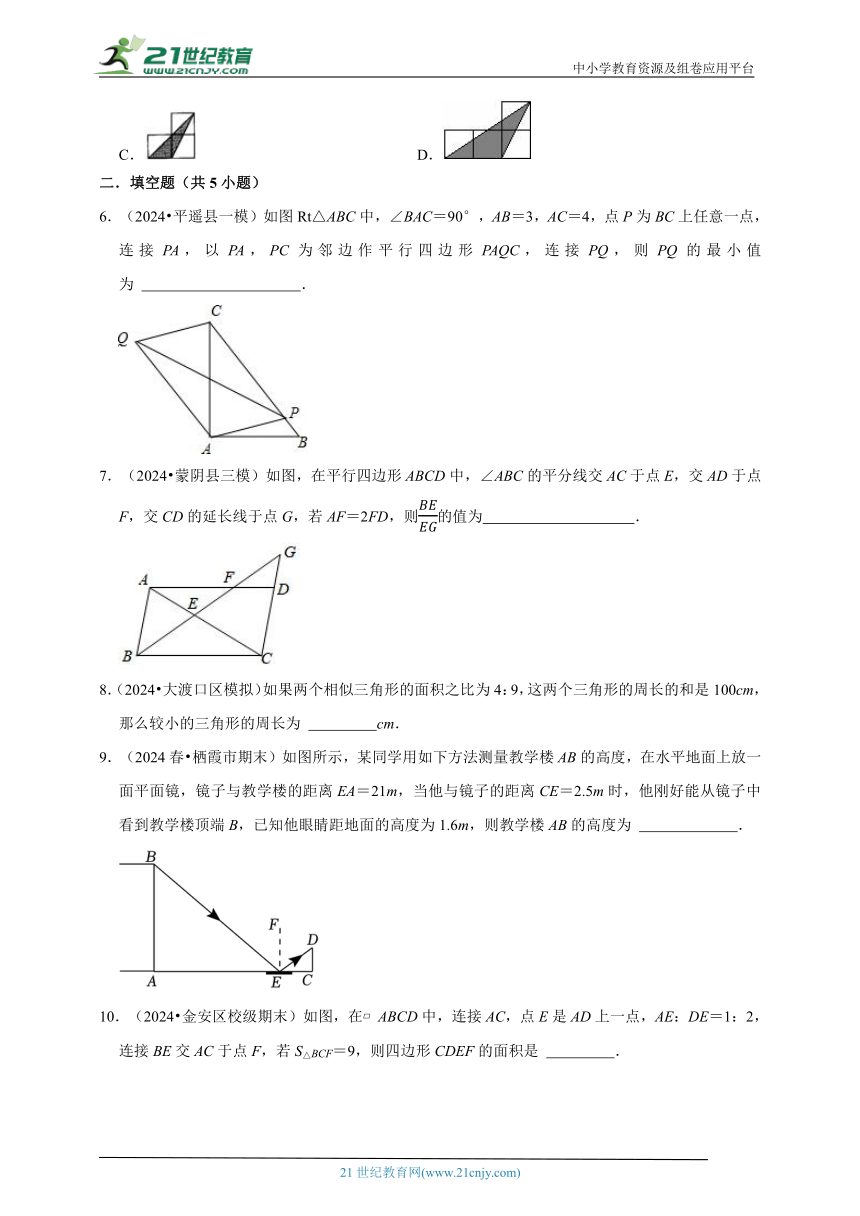
6.(2024 平遥县一模)如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
7.(2024 蒙阴县三模)如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为 .
8.(2024 大渡口区模拟)如果两个相似三角形的面积之比为4:9,这两个三角形的周长的和是100cm,那么较小的三角形的周长为 cm.
9.(2024春 栖霞市期末)如图所示,某同学用如下方法测量教学楼AB的高度,在水平地面上放一面平面镜,镜子与教学楼的距离EA=21m,当他与镜子的距离CE=2.5m时,他刚好能从镜子中看到教学楼顶端B,已知他眼睛距地面的高度为1.6m,则教学楼AB的高度为 .
10.(2024 金安区校级期末)如图,在 ABCD中,连接AC,点E是AD上一点,AE:DE=1:2,连接BE交AC于点F,若S△BCF=9,则四边形CDEF的面积是 .
三.解答题(共5小题)
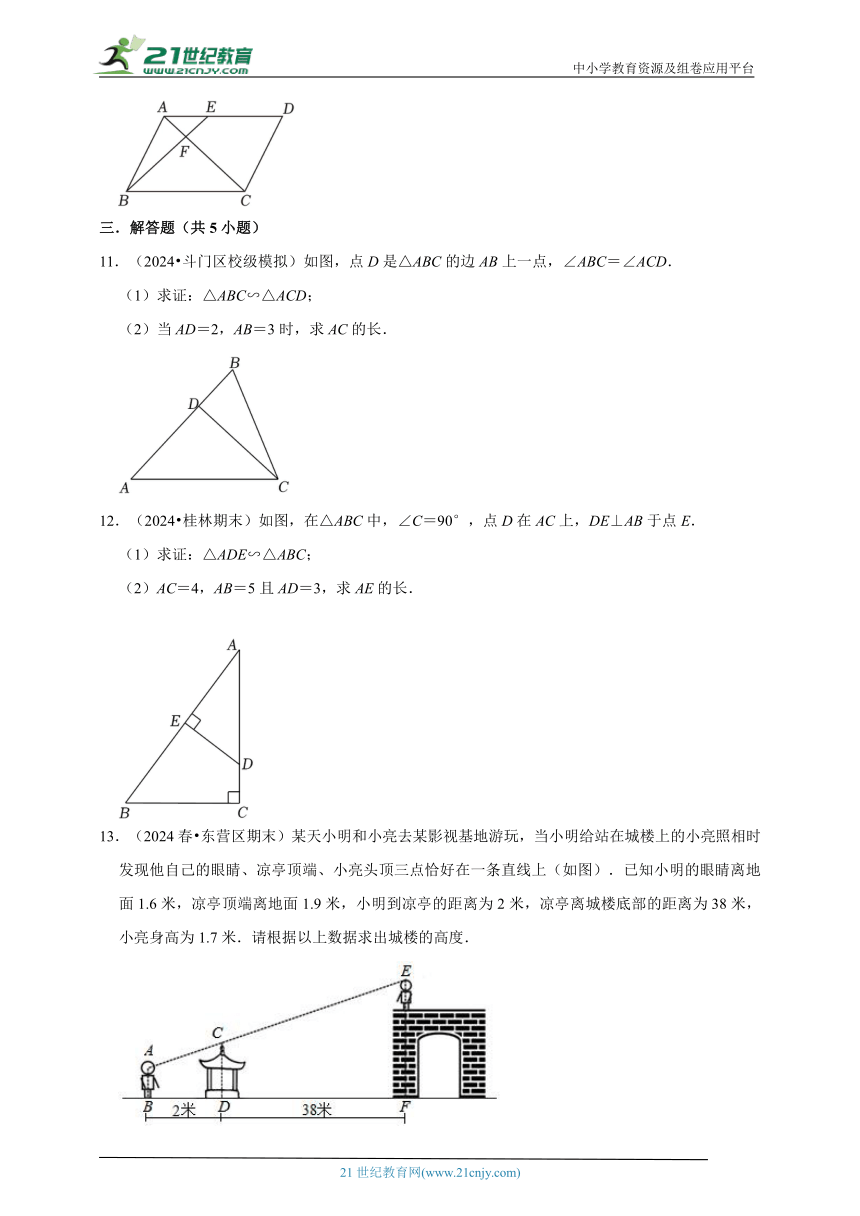
11.(2024 斗门区校级模拟)如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)当AD=2,AB=3时,求AC的长.
12.(2024 桂林期末)如图,在△ABC中,∠C=90°,点D在AC上,DE⊥AB于点E.
(1)求证:△ADE∽△ABC;
(2)AC=4,AB=5且AD=3,求AE的长.
13.(2024春 东营区期末)某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.6米,凉亭顶端离地面1.9米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.请根据以上数据求出城楼的高度.
14.(2024 鞍山模拟)在△ABC中,AB=2,将△ABC绕点B逆时针旋转得到△MBN,且CN∥BM,MA的延长线与CN交于点P,若AM=3,.
(1)求证:△ABM∽△CBN;
(2)求AP的长.
15.(2024 杨浦区四模)如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
新课预习衔接 相似三角形
参考答案与试题解析
一.选择题(共5小题)
1.(2024 合水县一模)若△ABC∽△DEF,S△ABC:S△DEF=2:3,则△ABC与△DEF的相似比为( )
A.2:3 B.4:9 C. D.3:2
【考点】相似三角形的性质.
【专题】图形的相似;运算能力.
【答案】C
【分析】由△ABC∽△DEF,S△ABC:S△DEF=2:3,根据相似三角形的面积比等于相似比的平方,即可求得答案.
【解答】解:∵△ABC∽△DEF,S△ABC:S△DEF=2:3,
∴△ABC与△DEF的相似比为::.
故选:C.
【点评】此题考查了相似三角形的性质.注意相似三角形面积的比等于相似比的平方.
2.(2024 洪山区校级二模)如图,在平行四边形ABCD中,点E在边AB上,连接DE,交对角线AC于点F,如果,CD=6,那么BE的值为( )
A.2 B.3 C.4 D.5
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】图形的相似;推理能力.
【答案】A
【分析】根据三角形面积的关系推出,再根据平行四边形的性质AB∥CD,从而推出△AEF∽△CDF,进而利用相似三角形的性质求解即可.
【解答】解:设△ADC中AC边上的高为h,
则S△ADFAF×h,S△DFCFC×h,
∵,
∴,
∵平行四边形ABCD中AB∥CD,
∴△AEF∽△CDF,
∴,即,
解得AE=4,
∵AB=CD=6,
∴BE=AB﹣AE=6﹣4=2,
故选:A.
【点评】本题考查相似三角形的判定与性质及平行四边形的性质,解题的关键是结合图形由三角形面积的关系推出,注意充分运用数形结合的思想方法.
3.(2024 昭阳区一模)如图,D,E是△ABC边AB,AC边上的两点,且DE∥BC,若S△ADE:S△ABC=1:16,则△ADE与△ABC的周长之比为( )
A.1:2 B.1:4 C.1:5 D.1:16
【考点】相似三角形的判定与性质.
【专题】三角形;图形的相似;推理能力.
【答案】B
【分析】由平行易证△ADE∽△ABC,由面积比等于相似比的平方,周长比等于相似比求解.
【解答】解:∵DE∥BC,
∴∠ADE=∠B,
∴△ADE∽△ABC
∵S△ADE:S△ABC=1:16
∴△ADE与△ABC周长之比为1:4,
故选:B.
【点评】本题考查相似三角形的判定和性质,熟练掌握相似三角形性质是解题的关键.
4.(2024 沭阳县校级月考)如图,已知∠1=∠2,那么添加下列的一个条件后,仍无法判定△ABC∽△ADE的是( )
A. B.∠B=∠D C. D.∠C=∠AED
【考点】相似三角形的判定.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
【解答】解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=∠BAC,
∴选项B、D根据两角对应相等判定△ABC∽△ADE,
选项A根据两边成比例夹角相等判定△ABC∽△ADE,
选项C中不是夹这两个角的边,所以不相似,
故选:C.
【点评】此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.
5.(2024 济南三模)如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
【考点】相似三角形的判定.
【答案】A
【分析】根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.
【解答】解:根据题意得:AB,AC=2,BC,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
【点评】此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.
二.填空题(共5小题)
6.(2024 平遥县一模)如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
【考点】相似三角形的判定与性质;垂线段最短;勾股定理;平行四边形的性质.
【专题】压轴题.
【答案】见试题解答内容
【分析】以PA,PC为邻边作平行四边形PAQC,由平行四边形的性质可知O是AC中点,PQ最短也就是PO最短,所以应该过O作BC的垂线P′O,然后根据△P′OC和△ABC相似,利用相似三角形的性质即可求出PQ的最小值.
【解答】解:∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴,
∴,
∴OP′,
∴则PQ的最小值为2OP′,
方法二:不用相似的方法,只利用等面积得,OC AB=BC OP',求得OP′,而其他部分的步骤共用.
故答案为:.
【点评】本题考查了勾股定理的运用、平行四边形的性质、相似三角形的判定和性质以及垂线段最短的性质,解题的关键是做高线各种相似三角形.
7.(2024 蒙阴县三模)如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为 .
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】多边形与平行四边形;图形的相似;推理能力.
【答案】.
【分析】由AF=2DF,可以设DF=k,则AF=2k,AD=3k,证明AB=AF=2k,DF=DG=k,再利用相似三角形的性质即可解决问题.
【解答】解:由AF=2DF,可以设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠AFB=∠FBC=∠DFG,∠ABF=∠G,
∵BE平分∠ABC,
∴∠ABF=∠CBG,
∴∠ABF=∠AFB=∠DFG=∠G,
∴AB=CD=2k,DF=DG=k,
∴CG=CD+DG=3k,
∵AB∥DG,
∴△ABE∽△CGE,
∴,
故答案为:.
【点评】本题考查平行四边形的性质,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
8.(2024 大渡口区模拟)如果两个相似三角形的面积之比为4:9,这两个三角形的周长的和是100cm,那么较小的三角形的周长为 40 cm.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】40.
【分析】根据相似三角形周长比等于面积比的算术平方根列式计算.
【解答】解:设较小的三角形的周长为x cm,则较大的三角形的周长为(100﹣x)cm,
∵两个相似三角形的面积之比为4:9,
∴两个相似三角形的相似比为2:3,
∴两个相似三角形的周长比为2:3,
∴,
解得x=40,
故答案为:40.
【点评】本题考查的是相似三角形的性质,掌握相似三角形周长比等于相似比是解题的关键.
9.(2024春 栖霞市期末)如图所示,某同学用如下方法测量教学楼AB的高度,在水平地面上放一面平面镜,镜子与教学楼的距离EA=21m,当他与镜子的距离CE=2.5m时,他刚好能从镜子中看到教学楼顶端B,已知他眼睛距地面的高度为1.6m,则教学楼AB的高度为 13.44m .
【考点】相似三角形的应用.
【专题】解直角三角形及其应用;推理能力.
【答案】13.44m.
【分析】先根据题意得出△BAE∽△DCE,再由相似三角形的对应边成比例计算即可.
【解答】解:依据题意,得∠DEF=∠BEF,
∵∠DEF+∠DEC=90°,∠BEF+∠BEA=90°,
∴∠DEC=∠BEA,
∵∠BAE=∠DCE=90°,
∴△BAE∽△DCE,
∴,
即,
∴AB=13.44m,
∴教学楼AB的高度为13.44m.
故答案为:13.44m.
【点评】本题考查相似三角形的判定和性质,先根据题意得出△BAE∽△DCE,再由相似三角形的对应边成比例计算是解题的关键.
10.(2024 金安区校级期末)如图,在 ABCD中,连接AC,点E是AD上一点,AE:DE=1:2,连接BE交AC于点F,若S△BCF=9,则四边形CDEF的面积是 11 .
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】三角形;多边形与平行四边形;图形的相似;运算能力;推理能力.
【答案】11.
【分析】先根据平行四边形的性质得AD∥BC,AD=BC,由AE:DE=1:2得AE:BC=1:3,证明△AFE∽△CFB得,进而得到△AFB,△AEF的面积,即可得△ABC的面积,再根据平行四边形的性质即可得解.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE:DE=1:2,
∴AE:AD=1:3,
∵AD=BC,
∴AE:BC=1:3,
∵AD∥BC,
∴△AFE∽△CFB,
∴,
∴,3,
∵S△BCF=9,
∴S△AEF=1,
∴S△ACD=S△ABC=S△BCF+S△AFB=12,
∴S四边形CDEF=S△ACD﹣S△AEF=12﹣1=11.
故答案为:11.
【点评】本题主要考查相似三角形的判定与性质,平行四边形的性质等,解此题的关键在于熟练掌握其知识点.
三.解答题(共5小题)
11.(2024 斗门区校级模拟)如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)当AD=2,AB=3时,求AC的长.
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)见解答;
(2).
【分析】(1)利用∠ABC=∠ACD,加上∠CAB=∠DAC,则根据相似三角形的判定方法可得到结论;
(2)由于△ABC∽△ACD,则利用相似比可求出AC的长.
【解答】(1)证明:∵∠ABC=∠ACD,∠CAB=∠DAC,
∴△ABC∽△ACD;
(2)解:∵△ABC∽△ACD,
∴,即,
∴AC.
【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.利用相似三角形的性质可以计算相应线段的长.
12.(2024 桂林期末)如图,在△ABC中,∠C=90°,点D在AC上,DE⊥AB于点E.
(1)求证:△ADE∽△ABC;
(2)AC=4,AB=5且AD=3,求AE的长.
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)证明见解答过程;
(2).
【分析】(1)由DE⊥AB得到∠DEA=∠C=90°,然后得到△DEA∽△BCA;
(2)利用相似三角形的性质求得AE的长.
【解答】(1)证明:∵DE⊥AB于点E,∠C=90°,
∴∠AED=∠C=90°,
∵∠A=∠A,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,
∴,
∵AC=4,AB=5,AD=3,
∴,
∴AE.
【点评】本题考查相似三角形的判定与性质,掌握相似三角形的判定是解题的关键.
13.(2024春 东营区期末)某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.6米,凉亭顶端离地面1.9米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.请根据以上数据求出城楼的高度.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】见试题解答内容
【分析】根据题意构造直角三角形,进而利用相似三角形的判定与性质求出即可.
【解答】解:过点A作AM⊥EF于点M,交CD于点N,
由题意得:AN=2米,CN=1.9﹣1.6=0.3(米),MN=38米,
∵CN∥EM,
∴△ACN∽△AEM,
∴,
∴,
∴EM=6,
∵AB=MF=1.7米,
∴城楼的高度为:6+1.6﹣1.7=5.9(米).
【点评】本题考查了相似三角形的应用,构造直角三角形,利用相似三角形的判定证出△ACN∽△AEM是解题的关键.
14.(2024 鞍山模拟)在△ABC中,AB=2,将△ABC绕点B逆时针旋转得到△MBN,且CN∥BM,MA的延长线与CN交于点P,若AM=3,.
(1)求证:△ABM∽△CBN;
(2)求AP的长.
【考点】相似三角形的判定与性质;旋转的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;图形的相似;运算能力;推理能力.
【答案】(1)见解析;
(2)AP=2.
【分析】(1)由旋转易得AB=MB,BC=BN,∠ABC=∠MBN,进而可得,∠ABM=∠CBN,以此即可证明△ABM∽△CBN;
(2)由△ABM∽△CBN得∠BMA=∠BNC,由CN∥BM得∠BMA=∠APN,由BC=BN得∠BNC=∠BCN,以此可得∠APN=∠BCN,则BC∥MP,于是可知四边形BCPM为平行四边形,BC=PM,利用△ABM∽△CBN的对应边成比例,求得CB=5=PM,则AP=PM﹣AM.
【解答】(1)证明:∵将△ABC绕点B逆时针旋转得到△MBN,
∴AB=MB,BC=BN,∠ABC=∠MBN,
∴,
∴∠MBN+∠ABN=∠ABC+∠ABN,即∠ABM=∠CBN,
∴△ABM∽△CBN;
(2)解:由(1)知,△ABM∽△CBN,
∴∠BMA=∠BNC,
∵CN∥BM,
∴∠BMA=∠APN,
∴∠APN=∠BNC,
又∵BC=BN,
∴∠BNC=∠BCN,
∴∠APN=∠BCN,
∴BC∥MP,
∴四边形BCPM为平行四边形,
∴BC=PM,
∵△ABM∽△CBN,
∴,即,
∴CB=5=PM,
∴AP=PM﹣AM=5﹣3=2.
【点评】本题主要考查旋转的性质、相似三角形的判定与性质、平行线的判定与性质、平行四边形的判定与性质、等腰三角形的性质,解题关键是:(1)利用旋转的性质找出两三角形相似的条件;(2)利用相似三角形的性质和等腰三角形的性质推出四边形BCPM为平行四边形,以此得到CB=PM,再利用相似三角形的性质解决问题.
15.(2024 杨浦区四模)如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;菱形的判定;矩形的性质.
【专题】图形的全等;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)证明过程见解答;
(2)证明过程见解答.
【分析】(1)根据矩形的性质可得AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,根据垂直定义可得∠FAE=90°,从而可得∠BAF=∠DAE,进而可得△ABF∽△ADE,然后利用相似三角形的性质可得,再利用两边成比例且夹角相等的两个三角形相似证明,即可解答;
(2)根据角平分线的定义可得∠AFE=∠CFE,从而证明△AFE≌△CFE,进而可得AF=CF,AE=EC,然后再证△AFG≌△CFG,从而可得∠FAG=∠FCG,再结合(1)的结论可得∠DAE=∠FCG,最后利用等角的余角相等可得∠DCG=∠AED,从而可得AE∥CG,进而利用菱形的判定方法即可解答.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,
∴∠ABF=180°﹣∠ABC=90°,
∵AE⊥AF,
∴∠FAE=90°,
∴∠FAE﹣∠BAE=∠DAB﹣∠BAE,
∴∠BAF=∠DAE,
∵∠D=∠ABF=90°,
∴△ABF∽△ADE,
∴,
∴,
∵∠D=∠FAE=90°,
∴△AEF∽△DAC;
(2)如图:
∵FE平分∠AFB,
∴∠AFE=∠CFE,
∵∠FAE=∠BCD=90°,EF=EF,
∴△AFE≌△CFE(AAS),
∴AF=CF,AE=EC,
∵FG=FG,
∴△AFG≌△CFG(SAS),
∴∠FAG=∠FCG,
∵∠BAF=∠DAE,
∴∠DAE=∠FCG,
∵∠DAE+∠AED=90°,∠BCG+∠DCG=90°,
∴∠DCG=∠AED,
∴AE∥CG,
∵AB∥CD,
∴四边形AGCE是平行四边形,
∵AE=EC,
∴四边形AGCE为菱形.
【点评】本题考查了全等三角形的判定与性质,菱形的判定与性质,矩形的性质,相似三角形的判定与性质,熟练掌握全等三角形的判定与性质,以及相似三角形的判定与性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 相似三角形
一.选择题(共5小题)
1.(2024 合水县一模)若△ABC∽△DEF,S△ABC:S△DEF=2:3,则△ABC与△DEF的相似比为( )
A.2:3 B.4:9 C. D.3:2
2.(2024 洪山区校级二模)如图,在平行四边形ABCD中,点E在边AB上,连接DE,交对角线AC于点F,如果,CD=6,那么BE的值为( )
A.2 B.3 C.4 D.5
3.(2024 昭阳区一模)如图,D,E是△ABC边AB,AC边上的两点,且DE∥BC,若S△ADE:S△ABC=1:16,则△ADE与△ABC的周长之比为( )
A.1:2 B.1:4 C.1:5 D.1:16
4.(2024 沭阳县校级月考)如图,已知∠1=∠2,那么添加下列的一个条件后,仍无法判定△ABC∽△ADE的是( )
A. B.∠B=∠D C. D.∠C=∠AED
5.(2024 济南三模)如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
二.填空题(共5小题)
6.(2024 平遥县一模)如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
7.(2024 蒙阴县三模)如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为 .
8.(2024 大渡口区模拟)如果两个相似三角形的面积之比为4:9,这两个三角形的周长的和是100cm,那么较小的三角形的周长为 cm.
9.(2024春 栖霞市期末)如图所示,某同学用如下方法测量教学楼AB的高度,在水平地面上放一面平面镜,镜子与教学楼的距离EA=21m,当他与镜子的距离CE=2.5m时,他刚好能从镜子中看到教学楼顶端B,已知他眼睛距地面的高度为1.6m,则教学楼AB的高度为 .
10.(2024 金安区校级期末)如图,在 ABCD中,连接AC,点E是AD上一点,AE:DE=1:2,连接BE交AC于点F,若S△BCF=9,则四边形CDEF的面积是 .
三.解答题(共5小题)
11.(2024 斗门区校级模拟)如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)当AD=2,AB=3时,求AC的长.
12.(2024 桂林期末)如图,在△ABC中,∠C=90°,点D在AC上,DE⊥AB于点E.
(1)求证:△ADE∽△ABC;
(2)AC=4,AB=5且AD=3,求AE的长.
13.(2024春 东营区期末)某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.6米,凉亭顶端离地面1.9米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.请根据以上数据求出城楼的高度.
14.(2024 鞍山模拟)在△ABC中,AB=2,将△ABC绕点B逆时针旋转得到△MBN,且CN∥BM,MA的延长线与CN交于点P,若AM=3,.
(1)求证:△ABM∽△CBN;
(2)求AP的长.
15.(2024 杨浦区四模)如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
新课预习衔接 相似三角形
参考答案与试题解析
一.选择题(共5小题)
1.(2024 合水县一模)若△ABC∽△DEF,S△ABC:S△DEF=2:3,则△ABC与△DEF的相似比为( )
A.2:3 B.4:9 C. D.3:2
【考点】相似三角形的性质.
【专题】图形的相似;运算能力.
【答案】C
【分析】由△ABC∽△DEF,S△ABC:S△DEF=2:3,根据相似三角形的面积比等于相似比的平方,即可求得答案.
【解答】解:∵△ABC∽△DEF,S△ABC:S△DEF=2:3,
∴△ABC与△DEF的相似比为::.
故选:C.
【点评】此题考查了相似三角形的性质.注意相似三角形面积的比等于相似比的平方.
2.(2024 洪山区校级二模)如图,在平行四边形ABCD中,点E在边AB上,连接DE,交对角线AC于点F,如果,CD=6,那么BE的值为( )
A.2 B.3 C.4 D.5
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】图形的相似;推理能力.
【答案】A
【分析】根据三角形面积的关系推出,再根据平行四边形的性质AB∥CD,从而推出△AEF∽△CDF,进而利用相似三角形的性质求解即可.
【解答】解:设△ADC中AC边上的高为h,
则S△ADFAF×h,S△DFCFC×h,
∵,
∴,
∵平行四边形ABCD中AB∥CD,
∴△AEF∽△CDF,
∴,即,
解得AE=4,
∵AB=CD=6,
∴BE=AB﹣AE=6﹣4=2,
故选:A.
【点评】本题考查相似三角形的判定与性质及平行四边形的性质,解题的关键是结合图形由三角形面积的关系推出,注意充分运用数形结合的思想方法.
3.(2024 昭阳区一模)如图,D,E是△ABC边AB,AC边上的两点,且DE∥BC,若S△ADE:S△ABC=1:16,则△ADE与△ABC的周长之比为( )
A.1:2 B.1:4 C.1:5 D.1:16
【考点】相似三角形的判定与性质.
【专题】三角形;图形的相似;推理能力.
【答案】B
【分析】由平行易证△ADE∽△ABC,由面积比等于相似比的平方,周长比等于相似比求解.
【解答】解:∵DE∥BC,
∴∠ADE=∠B,
∴△ADE∽△ABC
∵S△ADE:S△ABC=1:16
∴△ADE与△ABC周长之比为1:4,
故选:B.
【点评】本题考查相似三角形的判定和性质,熟练掌握相似三角形性质是解题的关键.
4.(2024 沭阳县校级月考)如图,已知∠1=∠2,那么添加下列的一个条件后,仍无法判定△ABC∽△ADE的是( )
A. B.∠B=∠D C. D.∠C=∠AED
【考点】相似三角形的判定.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据已知及相似三角形的判定方法对各个选项进行分析,从而得到最后答案.
【解答】解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
∴∠DAE=∠BAC,
∴选项B、D根据两角对应相等判定△ABC∽△ADE,
选项A根据两边成比例夹角相等判定△ABC∽△ADE,
选项C中不是夹这两个角的边,所以不相似,
故选:C.
【点评】此题考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.
5.(2024 济南三模)如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
【考点】相似三角形的判定.
【答案】A
【分析】根据网格中的数据求出AB,AC,BC的长,求出三边之比,利用三边对应成比例的两三角形相似判断即可.
【解答】解:根据题意得:AB,AC=2,BC,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
【点评】此题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解本题的关键.
二.填空题(共5小题)
6.(2024 平遥县一模)如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为 .
【考点】相似三角形的判定与性质;垂线段最短;勾股定理;平行四边形的性质.
【专题】压轴题.
【答案】见试题解答内容
【分析】以PA,PC为邻边作平行四边形PAQC,由平行四边形的性质可知O是AC中点,PQ最短也就是PO最短,所以应该过O作BC的垂线P′O,然后根据△P′OC和△ABC相似,利用相似三角形的性质即可求出PQ的最小值.
【解答】解:∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴,
∴,
∴OP′,
∴则PQ的最小值为2OP′,
方法二:不用相似的方法,只利用等面积得,OC AB=BC OP',求得OP′,而其他部分的步骤共用.
故答案为:.
【点评】本题考查了勾股定理的运用、平行四边形的性质、相似三角形的判定和性质以及垂线段最短的性质,解题的关键是做高线各种相似三角形.
7.(2024 蒙阴县三模)如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2FD,则的值为 .
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】多边形与平行四边形;图形的相似;推理能力.
【答案】.
【分析】由AF=2DF,可以设DF=k,则AF=2k,AD=3k,证明AB=AF=2k,DF=DG=k,再利用相似三角形的性质即可解决问题.
【解答】解:由AF=2DF,可以设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠AFB=∠FBC=∠DFG,∠ABF=∠G,
∵BE平分∠ABC,
∴∠ABF=∠CBG,
∴∠ABF=∠AFB=∠DFG=∠G,
∴AB=CD=2k,DF=DG=k,
∴CG=CD+DG=3k,
∵AB∥DG,
∴△ABE∽△CGE,
∴,
故答案为:.
【点评】本题考查平行四边形的性质,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
8.(2024 大渡口区模拟)如果两个相似三角形的面积之比为4:9,这两个三角形的周长的和是100cm,那么较小的三角形的周长为 40 cm.
【考点】相似三角形的性质.
【专题】图形的相似;推理能力.
【答案】40.
【分析】根据相似三角形周长比等于面积比的算术平方根列式计算.
【解答】解:设较小的三角形的周长为x cm,则较大的三角形的周长为(100﹣x)cm,
∵两个相似三角形的面积之比为4:9,
∴两个相似三角形的相似比为2:3,
∴两个相似三角形的周长比为2:3,
∴,
解得x=40,
故答案为:40.
【点评】本题考查的是相似三角形的性质,掌握相似三角形周长比等于相似比是解题的关键.
9.(2024春 栖霞市期末)如图所示,某同学用如下方法测量教学楼AB的高度,在水平地面上放一面平面镜,镜子与教学楼的距离EA=21m,当他与镜子的距离CE=2.5m时,他刚好能从镜子中看到教学楼顶端B,已知他眼睛距地面的高度为1.6m,则教学楼AB的高度为 13.44m .
【考点】相似三角形的应用.
【专题】解直角三角形及其应用;推理能力.
【答案】13.44m.
【分析】先根据题意得出△BAE∽△DCE,再由相似三角形的对应边成比例计算即可.
【解答】解:依据题意,得∠DEF=∠BEF,
∵∠DEF+∠DEC=90°,∠BEF+∠BEA=90°,
∴∠DEC=∠BEA,
∵∠BAE=∠DCE=90°,
∴△BAE∽△DCE,
∴,
即,
∴AB=13.44m,
∴教学楼AB的高度为13.44m.
故答案为:13.44m.
【点评】本题考查相似三角形的判定和性质,先根据题意得出△BAE∽△DCE,再由相似三角形的对应边成比例计算是解题的关键.
10.(2024 金安区校级期末)如图,在 ABCD中,连接AC,点E是AD上一点,AE:DE=1:2,连接BE交AC于点F,若S△BCF=9,则四边形CDEF的面积是 11 .
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】三角形;多边形与平行四边形;图形的相似;运算能力;推理能力.
【答案】11.
【分析】先根据平行四边形的性质得AD∥BC,AD=BC,由AE:DE=1:2得AE:BC=1:3,证明△AFE∽△CFB得,进而得到△AFB,△AEF的面积,即可得△ABC的面积,再根据平行四边形的性质即可得解.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE:DE=1:2,
∴AE:AD=1:3,
∵AD=BC,
∴AE:BC=1:3,
∵AD∥BC,
∴△AFE∽△CFB,
∴,
∴,3,
∵S△BCF=9,
∴S△AEF=1,
∴S△ACD=S△ABC=S△BCF+S△AFB=12,
∴S四边形CDEF=S△ACD﹣S△AEF=12﹣1=11.
故答案为:11.
【点评】本题主要考查相似三角形的判定与性质,平行四边形的性质等,解此题的关键在于熟练掌握其知识点.
三.解答题(共5小题)
11.(2024 斗门区校级模拟)如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)当AD=2,AB=3时,求AC的长.
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)见解答;
(2).
【分析】(1)利用∠ABC=∠ACD,加上∠CAB=∠DAC,则根据相似三角形的判定方法可得到结论;
(2)由于△ABC∽△ACD,则利用相似比可求出AC的长.
【解答】(1)证明:∵∠ABC=∠ACD,∠CAB=∠DAC,
∴△ABC∽△ACD;
(2)解:∵△ABC∽△ACD,
∴,即,
∴AC.
【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.利用相似三角形的性质可以计算相应线段的长.
12.(2024 桂林期末)如图,在△ABC中,∠C=90°,点D在AC上,DE⊥AB于点E.
(1)求证:△ADE∽△ABC;
(2)AC=4,AB=5且AD=3,求AE的长.
【考点】相似三角形的判定与性质.
【专题】图形的相似;推理能力.
【答案】(1)证明见解答过程;
(2).
【分析】(1)由DE⊥AB得到∠DEA=∠C=90°,然后得到△DEA∽△BCA;
(2)利用相似三角形的性质求得AE的长.
【解答】(1)证明:∵DE⊥AB于点E,∠C=90°,
∴∠AED=∠C=90°,
∵∠A=∠A,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,
∴,
∵AC=4,AB=5,AD=3,
∴,
∴AE.
【点评】本题考查相似三角形的判定与性质,掌握相似三角形的判定是解题的关键.
13.(2024春 东营区期末)某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的眼睛离地面1.6米,凉亭顶端离地面1.9米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为38米,小亮身高为1.7米.请根据以上数据求出城楼的高度.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】见试题解答内容
【分析】根据题意构造直角三角形,进而利用相似三角形的判定与性质求出即可.
【解答】解:过点A作AM⊥EF于点M,交CD于点N,
由题意得:AN=2米,CN=1.9﹣1.6=0.3(米),MN=38米,
∵CN∥EM,
∴△ACN∽△AEM,
∴,
∴,
∴EM=6,
∵AB=MF=1.7米,
∴城楼的高度为:6+1.6﹣1.7=5.9(米).
【点评】本题考查了相似三角形的应用,构造直角三角形,利用相似三角形的判定证出△ACN∽△AEM是解题的关键.
14.(2024 鞍山模拟)在△ABC中,AB=2,将△ABC绕点B逆时针旋转得到△MBN,且CN∥BM,MA的延长线与CN交于点P,若AM=3,.
(1)求证:△ABM∽△CBN;
(2)求AP的长.
【考点】相似三角形的判定与性质;旋转的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;图形的相似;运算能力;推理能力.
【答案】(1)见解析;
(2)AP=2.
【分析】(1)由旋转易得AB=MB,BC=BN,∠ABC=∠MBN,进而可得,∠ABM=∠CBN,以此即可证明△ABM∽△CBN;
(2)由△ABM∽△CBN得∠BMA=∠BNC,由CN∥BM得∠BMA=∠APN,由BC=BN得∠BNC=∠BCN,以此可得∠APN=∠BCN,则BC∥MP,于是可知四边形BCPM为平行四边形,BC=PM,利用△ABM∽△CBN的对应边成比例,求得CB=5=PM,则AP=PM﹣AM.
【解答】(1)证明:∵将△ABC绕点B逆时针旋转得到△MBN,
∴AB=MB,BC=BN,∠ABC=∠MBN,
∴,
∴∠MBN+∠ABN=∠ABC+∠ABN,即∠ABM=∠CBN,
∴△ABM∽△CBN;
(2)解:由(1)知,△ABM∽△CBN,
∴∠BMA=∠BNC,
∵CN∥BM,
∴∠BMA=∠APN,
∴∠APN=∠BNC,
又∵BC=BN,
∴∠BNC=∠BCN,
∴∠APN=∠BCN,
∴BC∥MP,
∴四边形BCPM为平行四边形,
∴BC=PM,
∵△ABM∽△CBN,
∴,即,
∴CB=5=PM,
∴AP=PM﹣AM=5﹣3=2.
【点评】本题主要考查旋转的性质、相似三角形的判定与性质、平行线的判定与性质、平行四边形的判定与性质、等腰三角形的性质,解题关键是:(1)利用旋转的性质找出两三角形相似的条件;(2)利用相似三角形的性质和等腰三角形的性质推出四边形BCPM为平行四边形,以此得到CB=PM,再利用相似三角形的性质解决问题.
15.(2024 杨浦区四模)如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;菱形的判定;矩形的性质.
【专题】图形的全等;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)证明过程见解答;
(2)证明过程见解答.
【分析】(1)根据矩形的性质可得AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,根据垂直定义可得∠FAE=90°,从而可得∠BAF=∠DAE,进而可得△ABF∽△ADE,然后利用相似三角形的性质可得,再利用两边成比例且夹角相等的两个三角形相似证明,即可解答;
(2)根据角平分线的定义可得∠AFE=∠CFE,从而证明△AFE≌△CFE,进而可得AF=CF,AE=EC,然后再证△AFG≌△CFG,从而可得∠FAG=∠FCG,再结合(1)的结论可得∠DAE=∠FCG,最后利用等角的余角相等可得∠DCG=∠AED,从而可得AE∥CG,进而利用菱形的判定方法即可解答.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,
∴∠ABF=180°﹣∠ABC=90°,
∵AE⊥AF,
∴∠FAE=90°,
∴∠FAE﹣∠BAE=∠DAB﹣∠BAE,
∴∠BAF=∠DAE,
∵∠D=∠ABF=90°,
∴△ABF∽△ADE,
∴,
∴,
∵∠D=∠FAE=90°,
∴△AEF∽△DAC;
(2)如图:
∵FE平分∠AFB,
∴∠AFE=∠CFE,
∵∠FAE=∠BCD=90°,EF=EF,
∴△AFE≌△CFE(AAS),
∴AF=CF,AE=EC,
∵FG=FG,
∴△AFG≌△CFG(SAS),
∴∠FAG=∠FCG,
∵∠BAF=∠DAE,
∴∠DAE=∠FCG,
∵∠DAE+∠AED=90°,∠BCG+∠DCG=90°,
∴∠DCG=∠AED,
∴AE∥CG,
∵AB∥CD,
∴四边形AGCE是平行四边形,
∵AE=EC,
∴四边形AGCE为菱形.
【点评】本题考查了全等三角形的判定与性质,菱形的判定与性质,矩形的性质,相似三角形的判定与性质,熟练掌握全等三角形的判定与性质,以及相似三角形的判定与性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
