1.3《全等三角形的判定》复习题(含答案)八年级数学上册苏科版
文档属性
| 名称 | 1.3《全等三角形的判定》复习题(含答案)八年级数学上册苏科版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 20:11:54 | ||
图片预览

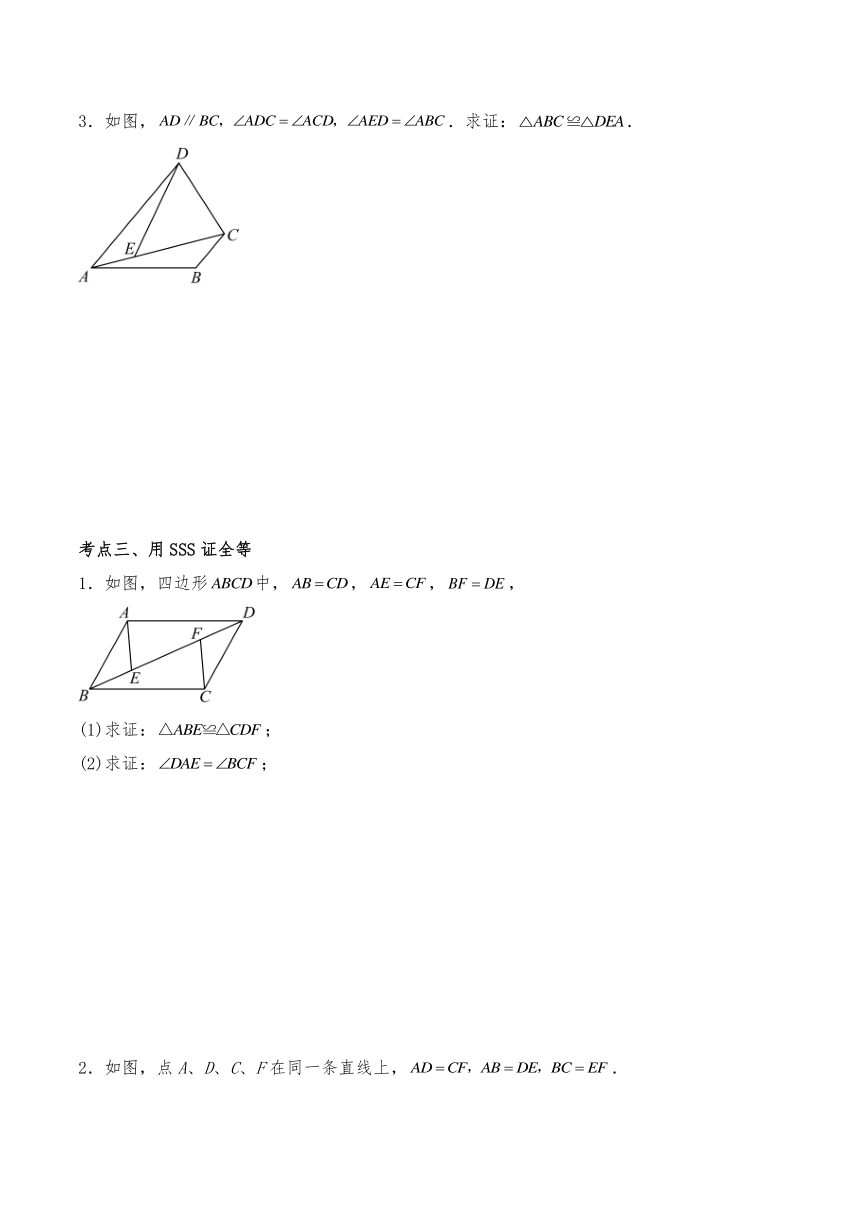

文档简介
1.3《全等三角形的判定》复习题
考点一、用ASA证全等
1.如图,点B,F,C,E在直线l上,点A,D在l的两侧,,,.
(1)求证:;
(2)若,,求的长.
2.如图,点D是 ABC的边延长线上一点,且,过D作,且,连接交于点F,若,求证:.
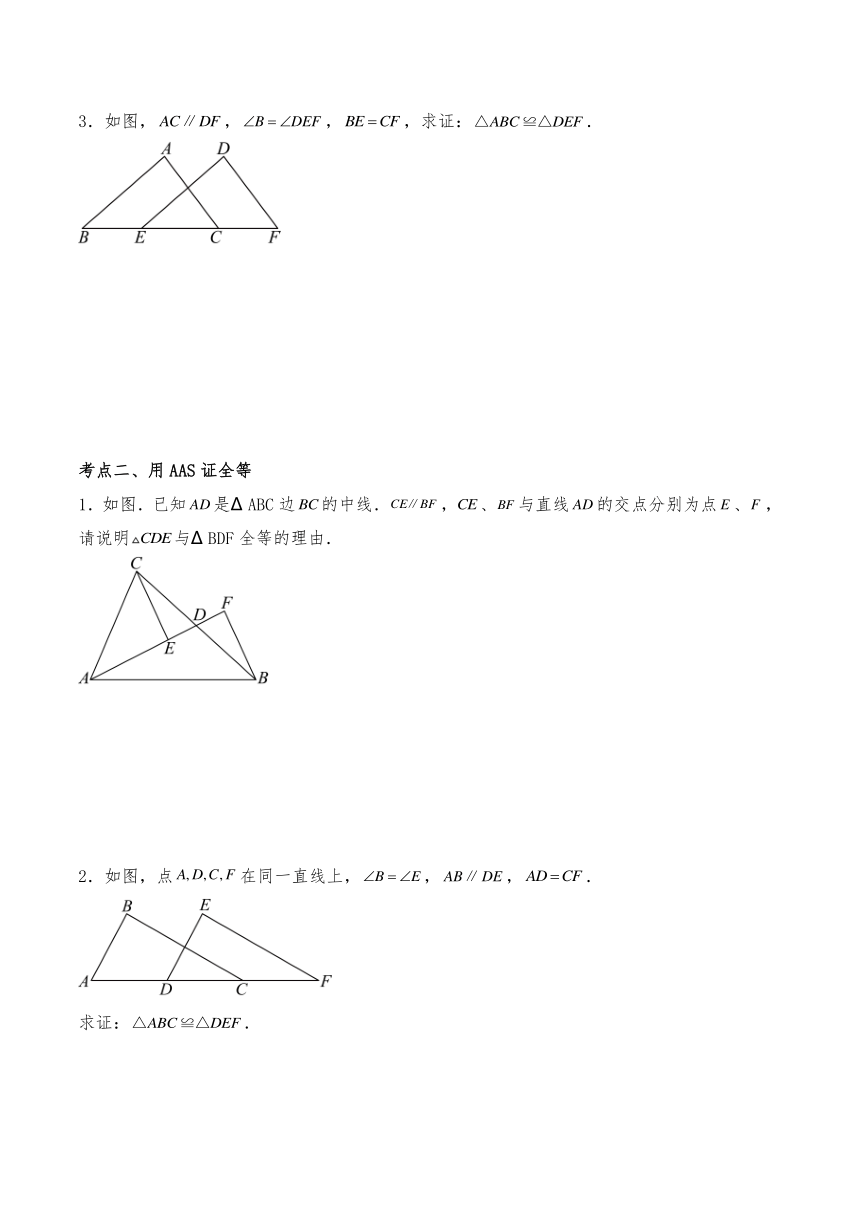
3.如图,,,,求证:.
考点二、用AAS证全等
1.如图.已知是 ABC边的中线.,、与直线的交点分别为点、,请说明与 BDF全等的理由.
2.如图,点在同一直线上,,,.
求证:.
3.如图,.求证:.
考点三、用SSS证全等
1.如图,四边形中,,,,
(1)求证:;
(2)求证:;
2.如图,点A、D、C、F在同一条直线上,.
(1)求证:;
(2)若,,求的度数.
3.如图,在 ABC中,,,为延长线上一点,点在上,且,.
(1)求证:;
(2)若,,求的长度;
(3)若,,求的度数.
考点四、用HL证全等
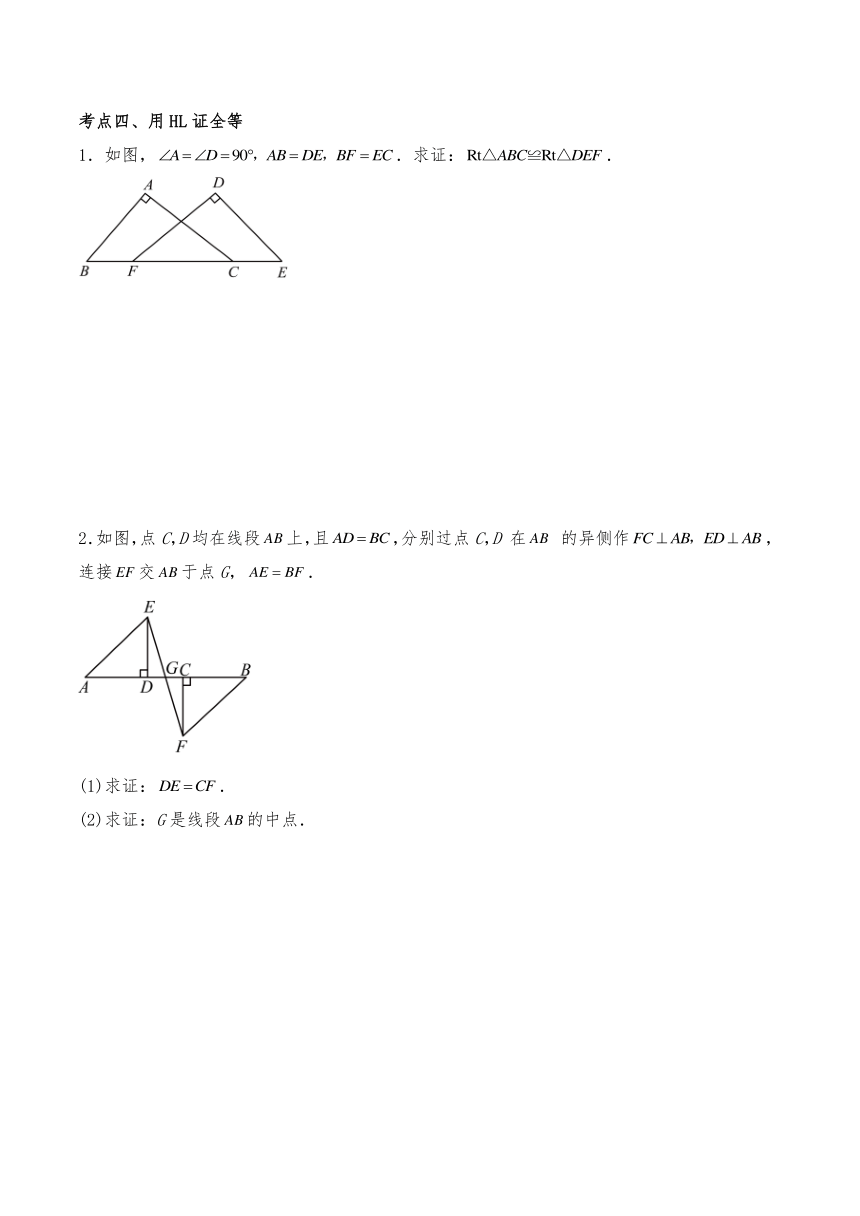
1.如图,.求证:.
2.如图,点C,D均在线段上,且,分别过点C,D 在 的异侧作,连接交于点G,.
(1)求证:.
(2)求证:G是线段的中点.
3.如图,于,于,若,.
(1)求证:;
(2)已知,,求的长.
考点五、特殊的SSA证全等
1.【问题呈现】如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.
把你画的三角形与其他同学画的三角形进行比较,所画的三角形都全等吗?此时,符合条件的三角形有多少种?
【问题探究】如图1,,请你用圆规在的另一边找到点C,使,这样的点C有____________个,说明符合条件的三角形有____________种;我们可以发现,此时(即“边边角”对应相等)两个三角形____________全等;
【拓展思考】如图2,已知,若且,那么一定是____________三角形(填“锐角”、“直角”或“钝角”).
2.
如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形. 把你画的三角形与其他同学画的三角形进行比较,所画的三角形都全等吗?此时,符合条件的三角形有多少种
(1)【操作】如图,,请你用圆规在的另一边找到点,使;
(2)【发现】(1)中的点有______个,说明符合条件的三角形有______种;此时(即“边边角”对应相等)两个三角形______全等.(填一定或不一定);
(3)【思考】如图,已知,若,则下列判断不正确的是( )
A.一定是钝角三角形 B.
C. D.的面积与的面积相等
3.如图,已知两条线段和一个角, 以长的线段为已知角的邻边,画一个三角形.
把你画的三角形与其他同学画的三角形进行比较,所画的三角形都全等吗?此时符合条件的角形有几种?
(1)[操作发现]
如图(1),通过作图我们可以发现,此时(即“边边角”对应相等)的两个三角形______全等(填“一定”或“不一定”).
(2)[探究证明]阅读并补全证明
已知:如图(2),在 ABC和中,,,.
求证:.
证明:在上取一点G,使,
∵,
∴______,
又∵,而,
∴______,
∵,
∴______,
又∵______,
∴(______),
∴(______).
考点六、全等模型———线三等角
1.如图,在 ABC中,,直线经过顶点,过,两点分别作的垂线,,,为垂足,且.求证:
(1);
(2).
2.通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,点A在直线l上,,过点B作于点C,过点D作交于点E.得.又,可以推理得到.进而得到结论:_____,_____.我们把这个数学模型称为“K字”模型或“一线三直角”模型;
(2)如图2,∠于点C,于点E,与直线交于点,求证:.
3.已知, ABC中,,,直线m过点A,且于D,于E,当直线m绕点A旋转至图1位置时,我们可以发现.
(1)当直线m绕点A旋转至图2位置时,问:与、的关系如何?请予证明;
(2)直线m在绕点A旋转一周的过程中,、、存在哪几种不同的数量关系?(直接写出,不必证明)
考点七、全等模型——手拉手
1.如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°能与BE重合,点F是ED与AB的交点.
(1)求证:AE=CD;
(2)若∠DBC=45°,求∠BFE的度数.
2.问题发现:如图1,已知为线段上一点,分别以线段,为直角边作等腰直角三角形,,,,连接,,线段,之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把绕点逆时针旋转,线段,交于点,则与之间的关系是否仍然成立?请说明理由.
3.如图,,,三点在一条直线上,和均为等边三角形,与交于点,与交于点.
(1)求证:;
(2)若把绕点任意旋转一个角度,(1)中的结论还成立吗?请说明理由.
考点八、全等模型——倍长中线
1.安安同学遇到这样一个问题:如图, ABC中,,,是中线,求的取值范围.
宁宁提示她可以延长到,使,连接,证明,经过推理和计算使问题得到解决.请解答:
(1)和全等吗?请说明理由;
(2)求出的取值范围.
2.(1)如图,在中,,,点G是的中点,求中线的取值范围;
(2)如图,在四边形中,,点E是的中点.若是的平分线.试探究,,之间的等量关系,并证明你的结论.
3.【发现问题】
(1)数学活动课上,马老师提出了如下问题:如图1,在 ABC中,,.是的中线,求的取值范围.
【探究方法】第一小组经过合作交流,得到了如下的解决方法:①延长到E,使得;②连接,通过三角形全等把、、转化在中;③利用三角形的三边关系可得的取值范围为,从而得到的取值范围是________;
方法总结:解题时,条件中若出现“中点”、“中线”字样,可以考虑倍长中线构造全等三角形
【问题解决】
(2)如图2,是 ABC的中线,是的中线,,下列四个选项中:直接写出所有正确选项的序号是________.
①;②;③;④
【问题拓展】
(3)如图3,,,与互补,连接、,E是的中点,试说明:;
(4)如图4,在(3)的条件下,若,延长交于点F,,,则的面积是________.
考点一、用ASA证全等
1.(1)证明:∵,
∴,
在 ABC与中
,
∴.
(2)解:∵,
∴,
∴,
∴,
∵,
∴.
2.证明:∵,,
∴,
∵,
∴,
∵,
∴,
∴.
3.证明:∵,
∴,
∵,
∴,
即,
在 ABC和中
,
∴.
考点二、用AAS证全等
1.解:与全等的理由如下:
∵是边的中线,
∴,
∵,
∴,
∴.
2.证明:,
,
,
,
,
在 ABC和中,,
.
3.证明:,
,
,
,即,
∵,
,
在 ABC与中,
,
.
考点三、用SSS证全等
1.(1)证明:,
,
即,
在和中,
(2)证明:由(1)可知,,
,
在和中,
,
,
,
即.
2.(1)
在 ABC与中
(2)
3.(1)证明:在和 CBF中,
,
;
(2)解:,
.
∵,
∴.
又,
.
,
,
;
(3)解:,,,,
,
,
,
,
,
.
考点四、用HL证全等
1.证明:,
,
即.
,
和都是直角三角形,
在和中,,
∴.
2.(1)∵,
∴,
∵,,
∴,
∴;
(2)∵,,,
∴,
∴,
即G是线段的中点.
3.(1)证明:,,
,
在和中,
,
,
;
(2)解:,,,
,
在和中,
,
,
.
考点五、特殊的SSA证全等
1.解:[问题探究]
如图,这样的点C有2个,说明符合条件的三角形有2种;我们可以发现,此时(即“边边角”对应相等)两个三角形不一定全等;
[拓展思考]
∵是钝角三角形,,
∴一定是钝角三角形;
故答案为:[问题探究]2,2,不一定;[拓展思考]钝角.
2.(1)解:如图所示:
点及即为所求;
(2)解:由(1)中所作图形可知,这样的点有2个,说明符合条件的三角形有2种;我们可以发现,此时(即“边边角”对应相等)两个三角形不一定全等,
故答案为:2,2,不一定;
(3)解:,是钝角三角形,
一定是钝角三角形,
故选:A.
3.(1)解:如图1,通过作图我们可以发现,此时(即“边边角”对应相等)的两个三角形不一定全等,
故答案为:不一定;
(2)证明:在上取一点G,使,
∵,
∴,
又∵,而,
∴,
∵,
∴,
又∵,
∴,
∴(全等三角形对应边相等),
故答案为:,,,,,全等三角形对应边相等.
考点六、全等模型———线三等角
1.(1)证明:,,
.
在和中,
,
.
∵∠EAC+∠ACE=90°,
,
即.
(2)解:,
.
又,,
.
2.(1))解:于点,于点,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,,
故答案为:,.
(2)证明:如图2,作于点,
∵于点,于点E,
∴,
由,
同理(1)得,
∴,
在和中,
∴,
∴.
3.(1)证明:如图2,
∵,,
∴,
∴.
∵,
∴,
∴.
在和中,
,
∴(AAS),
∴,
∵,
∴.
(2)直线m在绕点A旋转一周的过程中,、、存在3种不同的数量关系:,,.
如图1时,,
如图2时,,
如图3时,,(证明同理)
考点七、全等模型——手拉手
1.(1)证明:∵线段BD绕着点B按逆时针方向旋转120°能与BE重合,
∴BD=BE,∠EBD=120°,
∵AB=BC,∠ABC=120°,
∴∠ABD+∠DBC=∠ABD+∠ABE=120°,
∴∠DBC=∠ABE,
∴△ABE≌△CBD(SAS),
∴AE=CD;
(2)解:由(1)知∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,
∴∠BED=∠BDE=(180°﹣120°)=30°,
∴∠BFE=180°﹣∠BED﹣∠ABE
=180°﹣30°﹣45°=105°.
2.解:问题发现:延长BD,交AE于点F,如图所示:
∵,
∴,
又∵,
∴(SAS),
,
∵,
∴,
∴,
∴,
,
故答案为:,;
拓展探究:成立.
理由如下:设与相交于点,如图1所示:
∵,
∴,
又∵,,
∴(SAS),
∴,,
∵,
∴,
∴,
∴,
即,依然成立.
3.解:(1)证明:如图1中,与都是等边三角形,
,,,
,
,,
即.
在和中,
,
(SAS).
.
即AE=BD,
(2)成立;理由如下:
如图2中,、均为等边三角形,
,,,
,
即,
在和中,
,
,
.
考点八、全等模型——倍长中线
1.(1)解:∵是中线,
∴,
延长到,使,
又,
∴
(2)由(1)可知,,,
在中,,,
∴,即,
∴.
2.(1)解:延长DG至M,使GM=DG,连接MF,
在和中,
∴(SAS),
∴DE=MF=3,
∵DF -MF<DM<DF+MF,
∴7-3<DM<7+3,
即4<DM<10,
∵,
∴4<2DG<10,
∴2<DG<5;
(2)AD=CD+AB,理由如下:
解:延长AE,DC相交于点F,
∵,
∴∠BAE=∠F,
∵点E是BC的中点,
∴BE=CE,
在和中,
∴(AAS),
∴AB=CF,
∵∠BAE=∠F,∠DAF=∠BAE,
∴∠F=∠DAF,
∴AD=FD,
∵FD=CD+CF,CF=AB,
∴AD=CD+AB.
3.(1)解:如图1中,延长至点,使.
在和中,
,
,
,
,
,
,
;
(2)解:如图2,延长至,使,连接,
是中线,
,
又,,
,
,,
,,
,
为中线,
,
,
,
又,
,
,,
,
∴正确选项的序号是:②④;
(3)证明:如图3,延长至,使,连接,
是的中点,
,
又,,
,
,,
,
,
与互补,
,
,
又,,
,
,
;
(4),,
,,,
,
∵∠AOB=∠COD=90°,
,
,
,
,,
,
.
考点一、用ASA证全等
1.如图,点B,F,C,E在直线l上,点A,D在l的两侧,,,.
(1)求证:;
(2)若,,求的长.
2.如图,点D是 ABC的边延长线上一点,且,过D作,且,连接交于点F,若,求证:.
3.如图,,,,求证:.
考点二、用AAS证全等
1.如图.已知是 ABC边的中线.,、与直线的交点分别为点、,请说明与 BDF全等的理由.
2.如图,点在同一直线上,,,.
求证:.
3.如图,.求证:.
考点三、用SSS证全等
1.如图,四边形中,,,,
(1)求证:;
(2)求证:;
2.如图,点A、D、C、F在同一条直线上,.
(1)求证:;
(2)若,,求的度数.
3.如图,在 ABC中,,,为延长线上一点,点在上,且,.
(1)求证:;
(2)若,,求的长度;
(3)若,,求的度数.
考点四、用HL证全等
1.如图,.求证:.
2.如图,点C,D均在线段上,且,分别过点C,D 在 的异侧作,连接交于点G,.
(1)求证:.
(2)求证:G是线段的中点.
3.如图,于,于,若,.
(1)求证:;
(2)已知,,求的长.
考点五、特殊的SSA证全等
1.【问题呈现】如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.
把你画的三角形与其他同学画的三角形进行比较,所画的三角形都全等吗?此时,符合条件的三角形有多少种?
【问题探究】如图1,,请你用圆规在的另一边找到点C,使,这样的点C有____________个,说明符合条件的三角形有____________种;我们可以发现,此时(即“边边角”对应相等)两个三角形____________全等;
【拓展思考】如图2,已知,若且,那么一定是____________三角形(填“锐角”、“直角”或“钝角”).
2.
如图,已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形. 把你画的三角形与其他同学画的三角形进行比较,所画的三角形都全等吗?此时,符合条件的三角形有多少种
(1)【操作】如图,,请你用圆规在的另一边找到点,使;
(2)【发现】(1)中的点有______个,说明符合条件的三角形有______种;此时(即“边边角”对应相等)两个三角形______全等.(填一定或不一定);
(3)【思考】如图,已知,若,则下列判断不正确的是( )
A.一定是钝角三角形 B.
C. D.的面积与的面积相等
3.如图,已知两条线段和一个角, 以长的线段为已知角的邻边,画一个三角形.
把你画的三角形与其他同学画的三角形进行比较,所画的三角形都全等吗?此时符合条件的角形有几种?
(1)[操作发现]
如图(1),通过作图我们可以发现,此时(即“边边角”对应相等)的两个三角形______全等(填“一定”或“不一定”).
(2)[探究证明]阅读并补全证明
已知:如图(2),在 ABC和中,,,.
求证:.
证明:在上取一点G,使,
∵,
∴______,
又∵,而,
∴______,
∵,
∴______,
又∵______,
∴(______),
∴(______).
考点六、全等模型———线三等角
1.如图,在 ABC中,,直线经过顶点,过,两点分别作的垂线,,,为垂足,且.求证:
(1);
(2).
2.通过对下面数学模型的研究学习,解决下列问题:
(1)如图1,点A在直线l上,,过点B作于点C,过点D作交于点E.得.又,可以推理得到.进而得到结论:_____,_____.我们把这个数学模型称为“K字”模型或“一线三直角”模型;
(2)如图2,∠于点C,于点E,与直线交于点,求证:.
3.已知, ABC中,,,直线m过点A,且于D,于E,当直线m绕点A旋转至图1位置时,我们可以发现.
(1)当直线m绕点A旋转至图2位置时,问:与、的关系如何?请予证明;
(2)直线m在绕点A旋转一周的过程中,、、存在哪几种不同的数量关系?(直接写出,不必证明)
考点七、全等模型——手拉手
1.如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°能与BE重合,点F是ED与AB的交点.
(1)求证:AE=CD;
(2)若∠DBC=45°,求∠BFE的度数.
2.问题发现:如图1,已知为线段上一点,分别以线段,为直角边作等腰直角三角形,,,,连接,,线段,之间的数量关系为______;位置关系为_______.
拓展探究:如图2,把绕点逆时针旋转,线段,交于点,则与之间的关系是否仍然成立?请说明理由.
3.如图,,,三点在一条直线上,和均为等边三角形,与交于点,与交于点.
(1)求证:;
(2)若把绕点任意旋转一个角度,(1)中的结论还成立吗?请说明理由.
考点八、全等模型——倍长中线
1.安安同学遇到这样一个问题:如图, ABC中,,,是中线,求的取值范围.
宁宁提示她可以延长到,使,连接,证明,经过推理和计算使问题得到解决.请解答:
(1)和全等吗?请说明理由;
(2)求出的取值范围.
2.(1)如图,在中,,,点G是的中点,求中线的取值范围;
(2)如图,在四边形中,,点E是的中点.若是的平分线.试探究,,之间的等量关系,并证明你的结论.
3.【发现问题】
(1)数学活动课上,马老师提出了如下问题:如图1,在 ABC中,,.是的中线,求的取值范围.
【探究方法】第一小组经过合作交流,得到了如下的解决方法:①延长到E,使得;②连接,通过三角形全等把、、转化在中;③利用三角形的三边关系可得的取值范围为,从而得到的取值范围是________;
方法总结:解题时,条件中若出现“中点”、“中线”字样,可以考虑倍长中线构造全等三角形
【问题解决】
(2)如图2,是 ABC的中线,是的中线,,下列四个选项中:直接写出所有正确选项的序号是________.
①;②;③;④
【问题拓展】
(3)如图3,,,与互补,连接、,E是的中点,试说明:;
(4)如图4,在(3)的条件下,若,延长交于点F,,,则的面积是________.
考点一、用ASA证全等
1.(1)证明:∵,
∴,
在 ABC与中
,
∴.
(2)解:∵,
∴,
∴,
∴,
∵,
∴.
2.证明:∵,,
∴,
∵,
∴,
∵,
∴,
∴.
3.证明:∵,
∴,
∵,
∴,
即,
在 ABC和中
,
∴.
考点二、用AAS证全等
1.解:与全等的理由如下:
∵是边的中线,
∴,
∵,
∴,
∴.
2.证明:,
,
,
,
,
在 ABC和中,,
.
3.证明:,
,
,
,即,
∵,
,
在 ABC与中,
,
.
考点三、用SSS证全等
1.(1)证明:,
,
即,
在和中,
(2)证明:由(1)可知,,
,
在和中,
,
,
,
即.
2.(1)
在 ABC与中
(2)
3.(1)证明:在和 CBF中,
,
;
(2)解:,
.
∵,
∴.
又,
.
,
,
;
(3)解:,,,,
,
,
,
,
,
.
考点四、用HL证全等
1.证明:,
,
即.
,
和都是直角三角形,
在和中,,
∴.
2.(1)∵,
∴,
∵,,
∴,
∴;
(2)∵,,,
∴,
∴,
即G是线段的中点.
3.(1)证明:,,
,
在和中,
,
,
;
(2)解:,,,
,
在和中,
,
,
.
考点五、特殊的SSA证全等
1.解:[问题探究]
如图,这样的点C有2个,说明符合条件的三角形有2种;我们可以发现,此时(即“边边角”对应相等)两个三角形不一定全等;
[拓展思考]
∵是钝角三角形,,
∴一定是钝角三角形;
故答案为:[问题探究]2,2,不一定;[拓展思考]钝角.
2.(1)解:如图所示:
点及即为所求;
(2)解:由(1)中所作图形可知,这样的点有2个,说明符合条件的三角形有2种;我们可以发现,此时(即“边边角”对应相等)两个三角形不一定全等,
故答案为:2,2,不一定;
(3)解:,是钝角三角形,
一定是钝角三角形,
故选:A.
3.(1)解:如图1,通过作图我们可以发现,此时(即“边边角”对应相等)的两个三角形不一定全等,
故答案为:不一定;
(2)证明:在上取一点G,使,
∵,
∴,
又∵,而,
∴,
∵,
∴,
又∵,
∴,
∴(全等三角形对应边相等),
故答案为:,,,,,全等三角形对应边相等.
考点六、全等模型———线三等角
1.(1)证明:,,
.
在和中,
,
.
∵∠EAC+∠ACE=90°,
,
即.
(2)解:,
.
又,,
.
2.(1))解:于点,于点,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,,
故答案为:,.
(2)证明:如图2,作于点,
∵于点,于点E,
∴,
由,
同理(1)得,
∴,
在和中,
∴,
∴.
3.(1)证明:如图2,
∵,,
∴,
∴.
∵,
∴,
∴.
在和中,
,
∴(AAS),
∴,
∵,
∴.
(2)直线m在绕点A旋转一周的过程中,、、存在3种不同的数量关系:,,.
如图1时,,
如图2时,,
如图3时,,(证明同理)
考点七、全等模型——手拉手
1.(1)证明:∵线段BD绕着点B按逆时针方向旋转120°能与BE重合,
∴BD=BE,∠EBD=120°,
∵AB=BC,∠ABC=120°,
∴∠ABD+∠DBC=∠ABD+∠ABE=120°,
∴∠DBC=∠ABE,
∴△ABE≌△CBD(SAS),
∴AE=CD;
(2)解:由(1)知∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,
∴∠BED=∠BDE=(180°﹣120°)=30°,
∴∠BFE=180°﹣∠BED﹣∠ABE
=180°﹣30°﹣45°=105°.
2.解:问题发现:延长BD,交AE于点F,如图所示:
∵,
∴,
又∵,
∴(SAS),
,
∵,
∴,
∴,
∴,
,
故答案为:,;
拓展探究:成立.
理由如下:设与相交于点,如图1所示:
∵,
∴,
又∵,,
∴(SAS),
∴,,
∵,
∴,
∴,
∴,
即,依然成立.
3.解:(1)证明:如图1中,与都是等边三角形,
,,,
,
,,
即.
在和中,
,
(SAS).
.
即AE=BD,
(2)成立;理由如下:
如图2中,、均为等边三角形,
,,,
,
即,
在和中,
,
,
.
考点八、全等模型——倍长中线
1.(1)解:∵是中线,
∴,
延长到,使,
又,
∴
(2)由(1)可知,,,
在中,,,
∴,即,
∴.
2.(1)解:延长DG至M,使GM=DG,连接MF,
在和中,
∴(SAS),
∴DE=MF=3,
∵DF -MF<DM<DF+MF,
∴7-3<DM<7+3,
即4<DM<10,
∵,
∴4<2DG<10,
∴2<DG<5;
(2)AD=CD+AB,理由如下:
解:延长AE,DC相交于点F,
∵,
∴∠BAE=∠F,
∵点E是BC的中点,
∴BE=CE,
在和中,
∴(AAS),
∴AB=CF,
∵∠BAE=∠F,∠DAF=∠BAE,
∴∠F=∠DAF,
∴AD=FD,
∵FD=CD+CF,CF=AB,
∴AD=CD+AB.
3.(1)解:如图1中,延长至点,使.
在和中,
,
,
,
,
,
,
;
(2)解:如图2,延长至,使,连接,
是中线,
,
又,,
,
,,
,,
,
为中线,
,
,
,
又,
,
,,
,
∴正确选项的序号是:②④;
(3)证明:如图3,延长至,使,连接,
是的中点,
,
又,,
,
,,
,
,
与互补,
,
,
又,,
,
,
;
(4),,
,,,
,
∵∠AOB=∠COD=90°,
,
,
,
,,
,
.
同课章节目录
