1.3全等三角形的判定(SAS)(含答案)八年级数学上册苏科版
文档属性
| 名称 | 1.3全等三角形的判定(SAS)(含答案)八年级数学上册苏科版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 20:12:14 | ||
图片预览


文档简介
1.3全等三角形的判定(SAS)
考点一、全等三角形中的对应边与对应角
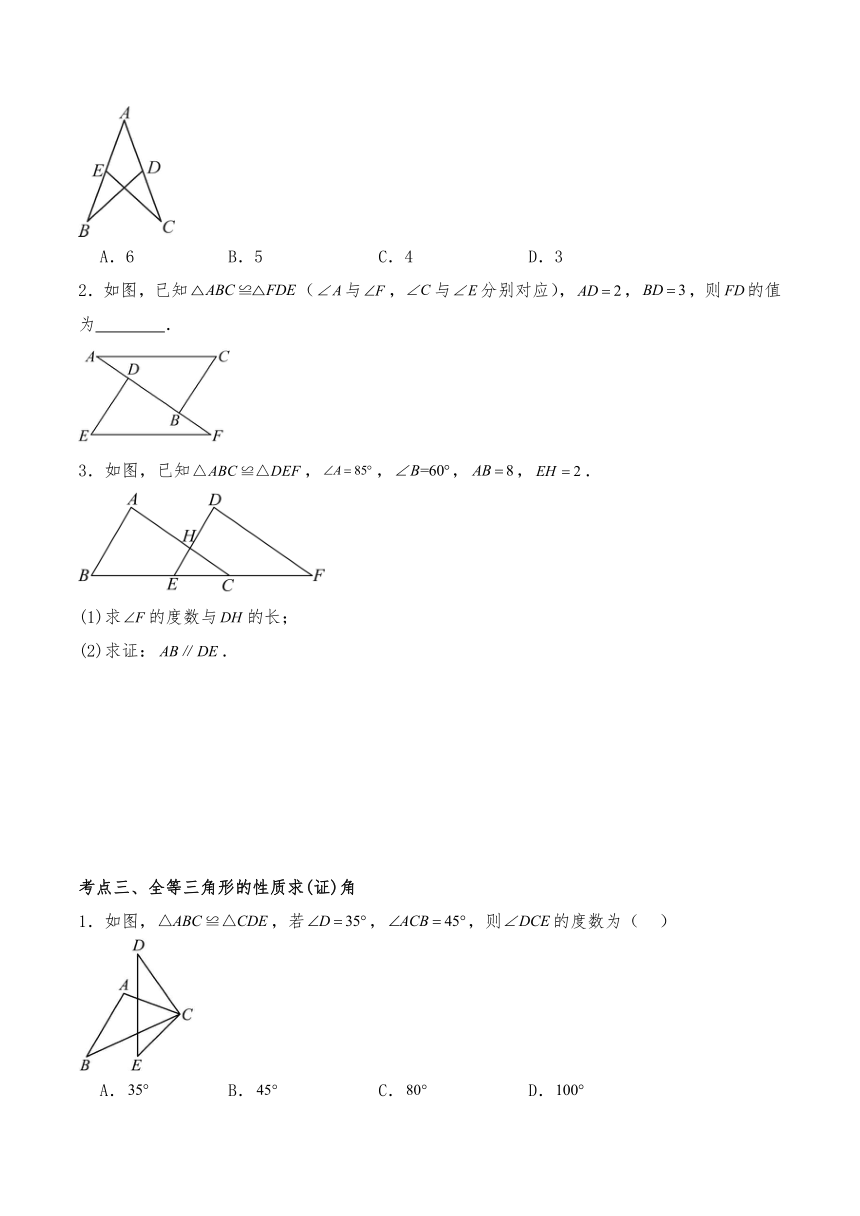
1.如图,, 和,和是对应边,则的对应角是( )
A. B. C. D.
2.如图所示,,其中与,与是对应顶点,则的对应边是 ,的对应角是 .
3.如图所示,在两个全等三角形中,点A和点E是一组对应顶点,写出其余的对应顶点、对应边和对应角.
考点二、全等三角形的性质求(证)边
1.如图,,若,,则的长度为( )
A.6 B.5 C.4 D.3
2.如图,已知(与,与分别对应),,,则的值为 .
3.如图,已知,,,,.
(1)求的度数与的长;
(2)求证:.
考点三、全等三角形的性质求(证)角
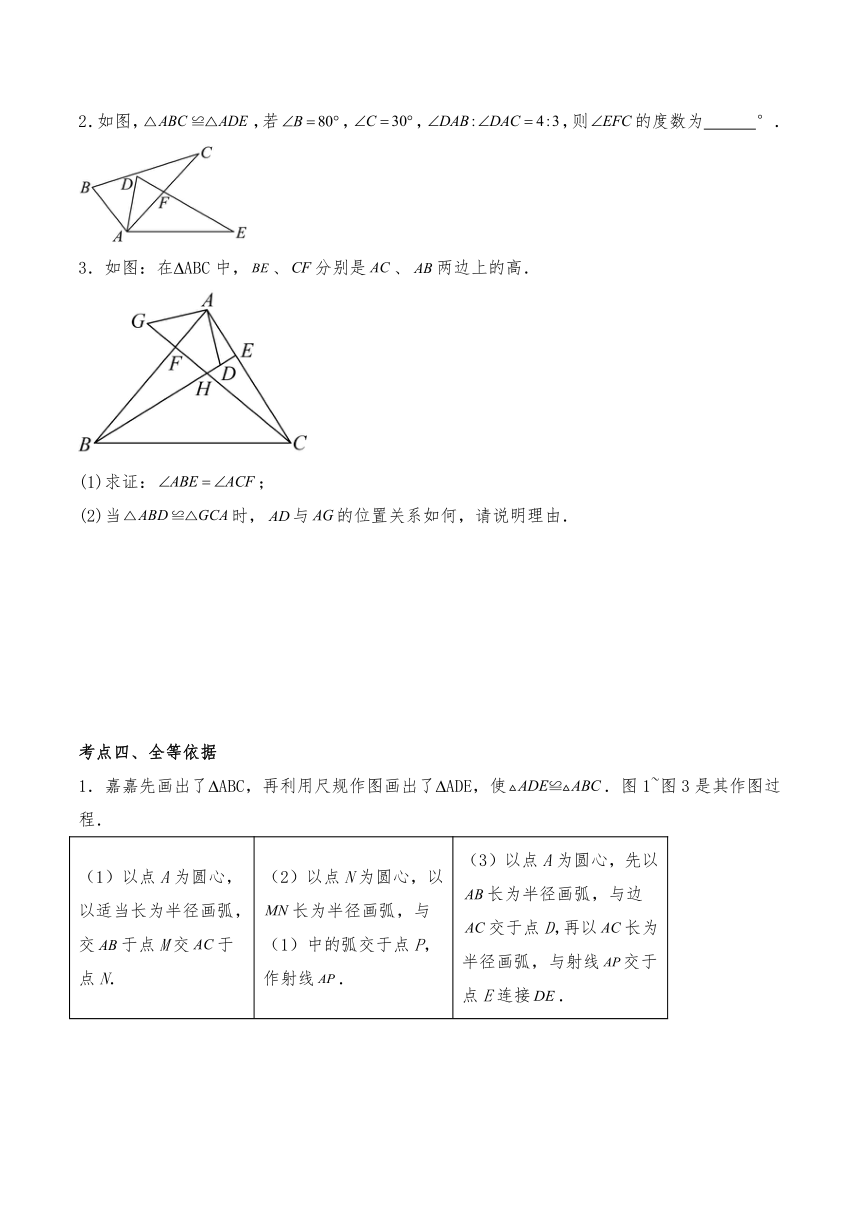
1.如图,,若,,则的度数为( )
A. B. C. D.
2.如图,,若,,,则的度数为 °.
3.如图:在 ABC中,、分别是、两边上的高.
(1)求证:;
(2)当时,与的位置关系如何,请说明理由.
考点四、全等依据
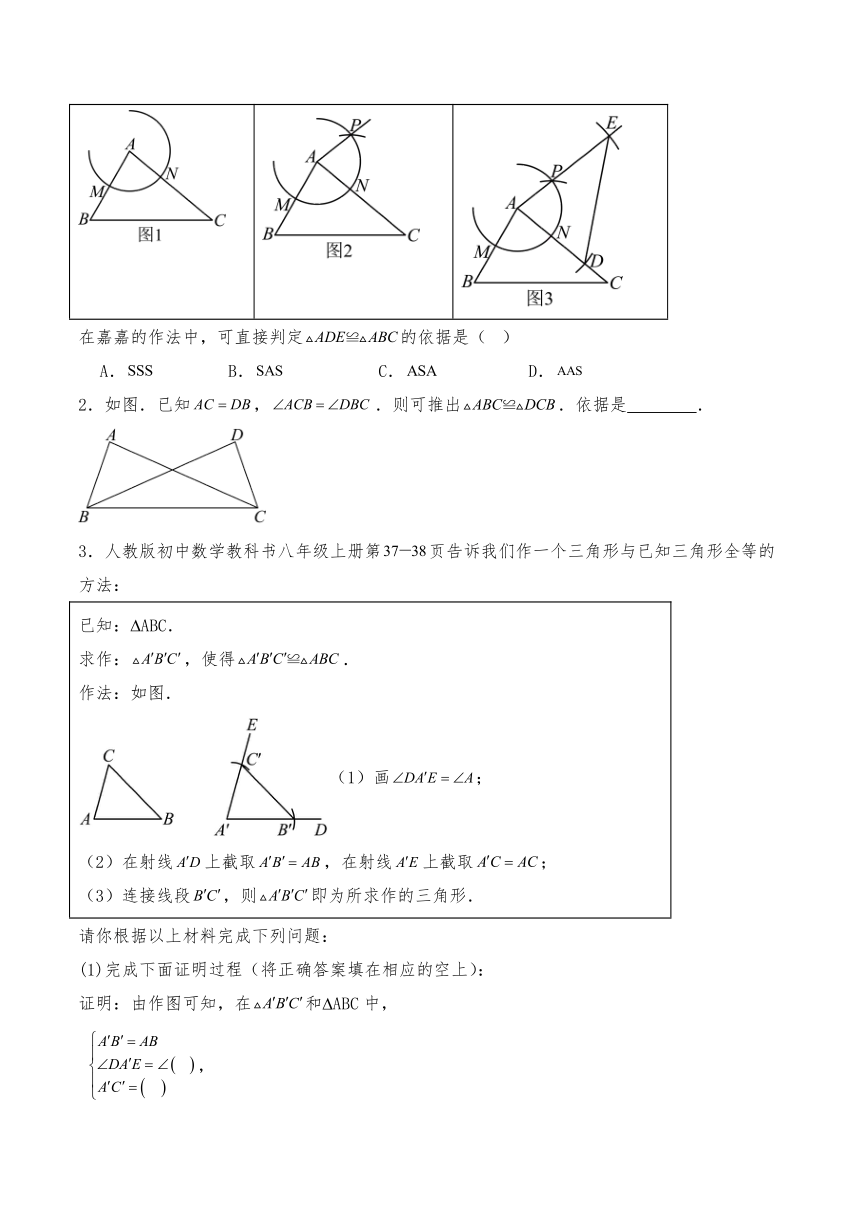
1.嘉嘉先画出了 ABC,再利用尺规作图画出了 ADE,使.图1~图3是其作图过程.
(1)以点A为圆心,以适当长为半径画弧,交于点M交于点N. (2)以点N为圆心,以长为半径画弧,与(1)中的弧交于点P,作射线. (3)以点A为圆心,先以长为半径画弧,与边交于点D,再以长为半径画弧,与射线交于点E连接.
在嘉嘉的作法中,可直接判定的依据是( )
A. B. C. D.
2.如图.已知,.则可推出.依据是 .
3.人教版初中数学教科书八年级上册第页告诉我们作一个三角形与已知三角形全等的方法:
已知: ABC. 求作:,使得. 作法:如图. (1)画; (2)在射线上截取,在射线上截取; (3)连接线段,则即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的空上):
证明:由作图可知,在和 ABC中,
,
.
(2)这种作一个三角形与已知三角形全等的方法的依据是 .(填序号)
① ② ③ ④
考点五、直接用SAS证全等
1.如图,已知点B,F,C,E在一条直线上,,,.求证:.
2.如图,已知,,,,求证:
3.如图,点,,,在同一条直线上,,,.求证:.
考点六、间接用SAS证全等
1.如图,已知点,在上,,,.求证:;
2.如图,在 ABC和中,,,,连接,.试说明:.
3.如图,已知点、是 ABC内两点,且,,,.
(1)求证:≌;
(2)延长、交于点,若,,求的度数.
考点七、全等三角形分割问题
1.手工劳动课上,老师给每个小组发一张硬纸板(如图),要求每个小组把它分成四个形状相同、面积相等的图形.他们该怎么分?请你试一试.
2.作图题
将的棋盘沿格线划分成两个全等图形,参考图例补全另外几种(约定某种划分法经过旋转、轴对称得到的划分法与原划分法相同).
3.沿着图中的虚线(小正方形虚线边),用四种不同的方法(构成4种不同图形)将下面的图形分成两个全等的图形.
考点八、全等三角形动点求t
1.如图,与相交于点,,,,点从点出发,沿方向以的速度运动,点从点出发,沿方向以的速度运动,,两点同时出发.当点返回点时,,两点同时停止运动.设点的运动时间为.
(1)试说明:;
(2)写出线段的长(用含的式子表示);
(3)连接,当线段经过点时,求的值.
2.如图,已知在 ABC中,,,D为的中点.点P在线段上以的速度由点B出发向终点C运动,同时点Q在线段上以的速度由点C出发向终点A运动,设点P的运动时间为.
(1)求的长;(用含的式子表示)
(2)若以为顶点的三角形和以为顶点的三角形全等,且和是对应角,求的值.
3.如图①,,,,垂足分别为A、B,.点在线段上以的速度由点向点运动,同时点从点B出发在射线上运动.它们运动的时间为(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当时,与是否全等?并判断此时线段和线段的位置关系,请分别说明理由;
(2)如图②,若“,”改为“”,点Q的运动速度为,其他条件不变,当与全等时,求出相应的x与t的值.
参考答案
考点一、全等三角形中的对应边与对应角
1.B
【分析】本此题主要考查了全等三角形的性质,准确识图,理解全等三角形的性质是解决问题的关键.
根据全等三角形的性质即可得出答案.
【详解】解:∵,
∴的对应角是.
故选:B.
2.
【分析】本题考查了全等三角形的对应边与对应角.解题的关键是牢记“全等三角形的对应边相等,对应角相等”即可.解题时要找对对应边,对应角即可.
【详解】解:∵,
∴,,
∴的对应边是,的对应角是.
故答案为:,.
3.解:对应顶点是点C和点C、点B和点D,对应边是和和和,对应角是和和和.
考点二、全等三角形的性质求(证)边
1.D
【分析】本题考查了全等三角形的性质,掌握全等三角形的性质“对应边相等”是关键.
根据全等三角形的性质得到,由即可求解.
【详解】解:,
∴,
∴,
故选:D .
2.5
【分析】本题考查全等三角形的性质,关键是掌握全等三角形的对应边相等.由全等三角形的对应边相等,即可得到答案.
【详解】解:∵,,
∴,
∵,
∴.
故答案为:5.
3.(1)解:∵,,
∴,
∵,,
∴,,
∵,
∴;
(2)证明:∵,
∴,
∴.
考点三、全等三角形的性质求(证)角
1.D
【分析】本题考查全等三角形的性质,三角形的内角和定理,解题的关键是掌握全等三角形的对应角相等.由全等三角形的对应角相等得到,再由三角形内角和定理即可求出的度数.
【详解】解:∵,
∴,
∵,
∴,
故选:.
2.
【分析】本题考查了全等三角形的性质和三角形内角和定理的应用,三角形外角的性质,解题的关键是掌握以上知识点,全等三角形的对应角相等,对应边相等.首先根据三角形内角和定理求出,然后根据全等三角形的性质得到,,最后利用三角形外角的性质求解即可.
【详解】解:∵,,
∴,
∵,
∴,
∵,
∴,,
∴,
∴.
故答案为:.
3.(1)解:∵、分别是、两边上的高.
∴,
∵,
∴
∴;
(2)解:,理由如下:
∵,
∴,
∵是两边上的高.
∴,
∴,
即,
∴,
∴.
考点四、全等依据
1.B
【分析】本题考查了尺规作图,全等三角形的判定.根据作图痕迹,利用即可证明.
【详解】解:由作图知,,,,
∴,
故答案为:B.
2.
【分析】本题考查的是三角形全等的判定:熟练掌握和,是解题的关键.
根据三角形全等的判定定理:两边和它们的夹角相等的两个三角形全等(“边角边”或“”) ,即可得出答案.
【详解】解:在与中,
,
∴,
即依据是两边和它们的夹角相等的两个三角形全等(“边角边”或“”).
故答案为:.
3.(1);;
(2)③
【分析】本题考查的知识点是全等三角形的判定,解题关键是掌握全等三角形判定的方法.
结合题意梳理已知条件,根据的全等三角形判定方法即可判定全等,结合判定过程填空即可.
【详解】(1)解:由题意可得:、、,
在和中,
,
,
故答案为:;;.
(2)解:由可得,这种作一个三角形与已知三角形全等的方法的依据是,
故答案为:③.
考点五、直接用SAS证全等
1.证明:∵,
∴,即,
∵,
∴,
在 ABC和中,
∴.
2.证明:∵,,
∴,
∴,
∴,
又∵,,
∴.
3.解:∵,
∴,
则,
∵,,
∴.
考点六、间接用SAS证全等
1.证明:∵,
∴,
∵,
∴,
在 ABC和 FDE中,
∴
2.解:因为,
所以,
所以.
在和中,,
所以.
3.(1),
,
,
在和中,
,
∴≌.
(2),
,
,
.
考点七、全等三角形分割问题
1.解:先将图根据标记的数字画出等面积的小格,然后以阴影部分为基本图形,可以分别得出下图所示的四种分法:
2.解:如图所示,(答案不唯一)
3.解:如图所示,即为所求;
考点八、全等三角形动点求t
1.(1)解: ,,,
,
,
所以.
(2)解:分两种情况:①当时,;
②当时,,
.
综上所述,线段的长为或.
(3)解: ,,,
,
.
分两种情况:①当时,,解得;
②当时,,解得.
综上所述,当线段经过点时,的值为1或2.
2.(1)∵,
∴;
(2)∵D为的中点,
∴,
∵,
∴,
∴当时,,
即,
解得;
当时,,
即,
解得;
综上所述,或.
3.(1)解:,线段和线段的位置关系是,理由如下:
,,
,
∵当时,,
,
,
在和中,
,
.
.
,
,
又,
,
.
(2)解:由题意可得:,,
∴,
∵
∴分两种情况讨论:
①若,则,,
可得,,
解得,;
②若,则,,
可得,,
解得,.
综上,当与 BPQ全等时,的值为3或.
考点一、全等三角形中的对应边与对应角
1.如图,, 和,和是对应边,则的对应角是( )
A. B. C. D.
2.如图所示,,其中与,与是对应顶点,则的对应边是 ,的对应角是 .
3.如图所示,在两个全等三角形中,点A和点E是一组对应顶点,写出其余的对应顶点、对应边和对应角.
考点二、全等三角形的性质求(证)边
1.如图,,若,,则的长度为( )
A.6 B.5 C.4 D.3
2.如图,已知(与,与分别对应),,,则的值为 .
3.如图,已知,,,,.
(1)求的度数与的长;
(2)求证:.
考点三、全等三角形的性质求(证)角
1.如图,,若,,则的度数为( )
A. B. C. D.
2.如图,,若,,,则的度数为 °.
3.如图:在 ABC中,、分别是、两边上的高.
(1)求证:;
(2)当时,与的位置关系如何,请说明理由.
考点四、全等依据
1.嘉嘉先画出了 ABC,再利用尺规作图画出了 ADE,使.图1~图3是其作图过程.
(1)以点A为圆心,以适当长为半径画弧,交于点M交于点N. (2)以点N为圆心,以长为半径画弧,与(1)中的弧交于点P,作射线. (3)以点A为圆心,先以长为半径画弧,与边交于点D,再以长为半径画弧,与射线交于点E连接.
在嘉嘉的作法中,可直接判定的依据是( )
A. B. C. D.
2.如图.已知,.则可推出.依据是 .
3.人教版初中数学教科书八年级上册第页告诉我们作一个三角形与已知三角形全等的方法:
已知: ABC. 求作:,使得. 作法:如图. (1)画; (2)在射线上截取,在射线上截取; (3)连接线段,则即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的空上):
证明:由作图可知,在和 ABC中,
,
.
(2)这种作一个三角形与已知三角形全等的方法的依据是 .(填序号)
① ② ③ ④
考点五、直接用SAS证全等
1.如图,已知点B,F,C,E在一条直线上,,,.求证:.
2.如图,已知,,,,求证:
3.如图,点,,,在同一条直线上,,,.求证:.
考点六、间接用SAS证全等
1.如图,已知点,在上,,,.求证:;
2.如图,在 ABC和中,,,,连接,.试说明:.
3.如图,已知点、是 ABC内两点,且,,,.
(1)求证:≌;
(2)延长、交于点,若,,求的度数.
考点七、全等三角形分割问题
1.手工劳动课上,老师给每个小组发一张硬纸板(如图),要求每个小组把它分成四个形状相同、面积相等的图形.他们该怎么分?请你试一试.
2.作图题
将的棋盘沿格线划分成两个全等图形,参考图例补全另外几种(约定某种划分法经过旋转、轴对称得到的划分法与原划分法相同).
3.沿着图中的虚线(小正方形虚线边),用四种不同的方法(构成4种不同图形)将下面的图形分成两个全等的图形.
考点八、全等三角形动点求t
1.如图,与相交于点,,,,点从点出发,沿方向以的速度运动,点从点出发,沿方向以的速度运动,,两点同时出发.当点返回点时,,两点同时停止运动.设点的运动时间为.
(1)试说明:;
(2)写出线段的长(用含的式子表示);
(3)连接,当线段经过点时,求的值.
2.如图,已知在 ABC中,,,D为的中点.点P在线段上以的速度由点B出发向终点C运动,同时点Q在线段上以的速度由点C出发向终点A运动,设点P的运动时间为.
(1)求的长;(用含的式子表示)
(2)若以为顶点的三角形和以为顶点的三角形全等,且和是对应角,求的值.
3.如图①,,,,垂足分别为A、B,.点在线段上以的速度由点向点运动,同时点从点B出发在射线上运动.它们运动的时间为(当点P运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当时,与是否全等?并判断此时线段和线段的位置关系,请分别说明理由;
(2)如图②,若“,”改为“”,点Q的运动速度为,其他条件不变,当与全等时,求出相应的x与t的值.
参考答案
考点一、全等三角形中的对应边与对应角
1.B
【分析】本此题主要考查了全等三角形的性质,准确识图,理解全等三角形的性质是解决问题的关键.
根据全等三角形的性质即可得出答案.
【详解】解:∵,
∴的对应角是.
故选:B.
2.
【分析】本题考查了全等三角形的对应边与对应角.解题的关键是牢记“全等三角形的对应边相等,对应角相等”即可.解题时要找对对应边,对应角即可.
【详解】解:∵,
∴,,
∴的对应边是,的对应角是.
故答案为:,.
3.解:对应顶点是点C和点C、点B和点D,对应边是和和和,对应角是和和和.
考点二、全等三角形的性质求(证)边
1.D
【分析】本题考查了全等三角形的性质,掌握全等三角形的性质“对应边相等”是关键.
根据全等三角形的性质得到,由即可求解.
【详解】解:,
∴,
∴,
故选:D .
2.5
【分析】本题考查全等三角形的性质,关键是掌握全等三角形的对应边相等.由全等三角形的对应边相等,即可得到答案.
【详解】解:∵,,
∴,
∵,
∴.
故答案为:5.
3.(1)解:∵,,
∴,
∵,,
∴,,
∵,
∴;
(2)证明:∵,
∴,
∴.
考点三、全等三角形的性质求(证)角
1.D
【分析】本题考查全等三角形的性质,三角形的内角和定理,解题的关键是掌握全等三角形的对应角相等.由全等三角形的对应角相等得到,再由三角形内角和定理即可求出的度数.
【详解】解:∵,
∴,
∵,
∴,
故选:.
2.
【分析】本题考查了全等三角形的性质和三角形内角和定理的应用,三角形外角的性质,解题的关键是掌握以上知识点,全等三角形的对应角相等,对应边相等.首先根据三角形内角和定理求出,然后根据全等三角形的性质得到,,最后利用三角形外角的性质求解即可.
【详解】解:∵,,
∴,
∵,
∴,
∵,
∴,,
∴,
∴.
故答案为:.
3.(1)解:∵、分别是、两边上的高.
∴,
∵,
∴
∴;
(2)解:,理由如下:
∵,
∴,
∵是两边上的高.
∴,
∴,
即,
∴,
∴.
考点四、全等依据
1.B
【分析】本题考查了尺规作图,全等三角形的判定.根据作图痕迹,利用即可证明.
【详解】解:由作图知,,,,
∴,
故答案为:B.
2.
【分析】本题考查的是三角形全等的判定:熟练掌握和,是解题的关键.
根据三角形全等的判定定理:两边和它们的夹角相等的两个三角形全等(“边角边”或“”) ,即可得出答案.
【详解】解:在与中,
,
∴,
即依据是两边和它们的夹角相等的两个三角形全等(“边角边”或“”).
故答案为:.
3.(1);;
(2)③
【分析】本题考查的知识点是全等三角形的判定,解题关键是掌握全等三角形判定的方法.
结合题意梳理已知条件,根据的全等三角形判定方法即可判定全等,结合判定过程填空即可.
【详解】(1)解:由题意可得:、、,
在和中,
,
,
故答案为:;;.
(2)解:由可得,这种作一个三角形与已知三角形全等的方法的依据是,
故答案为:③.
考点五、直接用SAS证全等
1.证明:∵,
∴,即,
∵,
∴,
在 ABC和中,
∴.
2.证明:∵,,
∴,
∴,
∴,
又∵,,
∴.
3.解:∵,
∴,
则,
∵,,
∴.
考点六、间接用SAS证全等
1.证明:∵,
∴,
∵,
∴,
在 ABC和 FDE中,
∴
2.解:因为,
所以,
所以.
在和中,,
所以.
3.(1),
,
,
在和中,
,
∴≌.
(2),
,
,
.
考点七、全等三角形分割问题
1.解:先将图根据标记的数字画出等面积的小格,然后以阴影部分为基本图形,可以分别得出下图所示的四种分法:
2.解:如图所示,(答案不唯一)
3.解:如图所示,即为所求;
考点八、全等三角形动点求t
1.(1)解: ,,,
,
,
所以.
(2)解:分两种情况:①当时,;
②当时,,
.
综上所述,线段的长为或.
(3)解: ,,,
,
.
分两种情况:①当时,,解得;
②当时,,解得.
综上所述,当线段经过点时,的值为1或2.
2.(1)∵,
∴;
(2)∵D为的中点,
∴,
∵,
∴,
∴当时,,
即,
解得;
当时,,
即,
解得;
综上所述,或.
3.(1)解:,线段和线段的位置关系是,理由如下:
,,
,
∵当时,,
,
,
在和中,
,
.
.
,
,
又,
,
.
(2)解:由题意可得:,,
∴,
∵
∴分两种情况讨论:
①若,则,,
可得,,
解得,;
②若,则,,
可得,,
解得,.
综上,当与 BPQ全等时,的值为3或.
同课章节目录
