2025年全国科学创新实践活动(原华数杯)二级组(小学五、六年级)数学竞赛试题(图片版,含答案)
文档属性
| 名称 | 2025年全国科学创新实践活动(原华数杯)二级组(小学五、六年级)数学竞赛试题(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 422.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 08:38:25 | ||
图片预览

文档简介
科学创新能力实践活动(二级组)
(2025年2月22日时长90分钟)
题号
2
3
4
5
6
7
P
10
总成绩
得分
其
评阅人
填空题(共十题,每题10分,共100分)
p
1.用若干个长为5厘米,宽为4厘米的长方形纸板拼成的最小正方形的面积是
平方厘米.
2.设1×2×3×…×2024=35n×A,其中n与A为自然数,那么n的最大值是
製
舞
3.标有A、B、C、D、E、F、G记号的七盏灯顺次排成一行,每盏灯安装一个
开关,现在A、B、C三盏灯亮着,其余四盏灯是灭的.小明先拉一下A的开关,
然后拉B、C…直到G的开关各一次,之后再按A到G的顺序拉动开关,并以
此循环.他拉动了2024次后,标有
记号的灯此时是亮的.(写
出全部亮着的灯的标号)
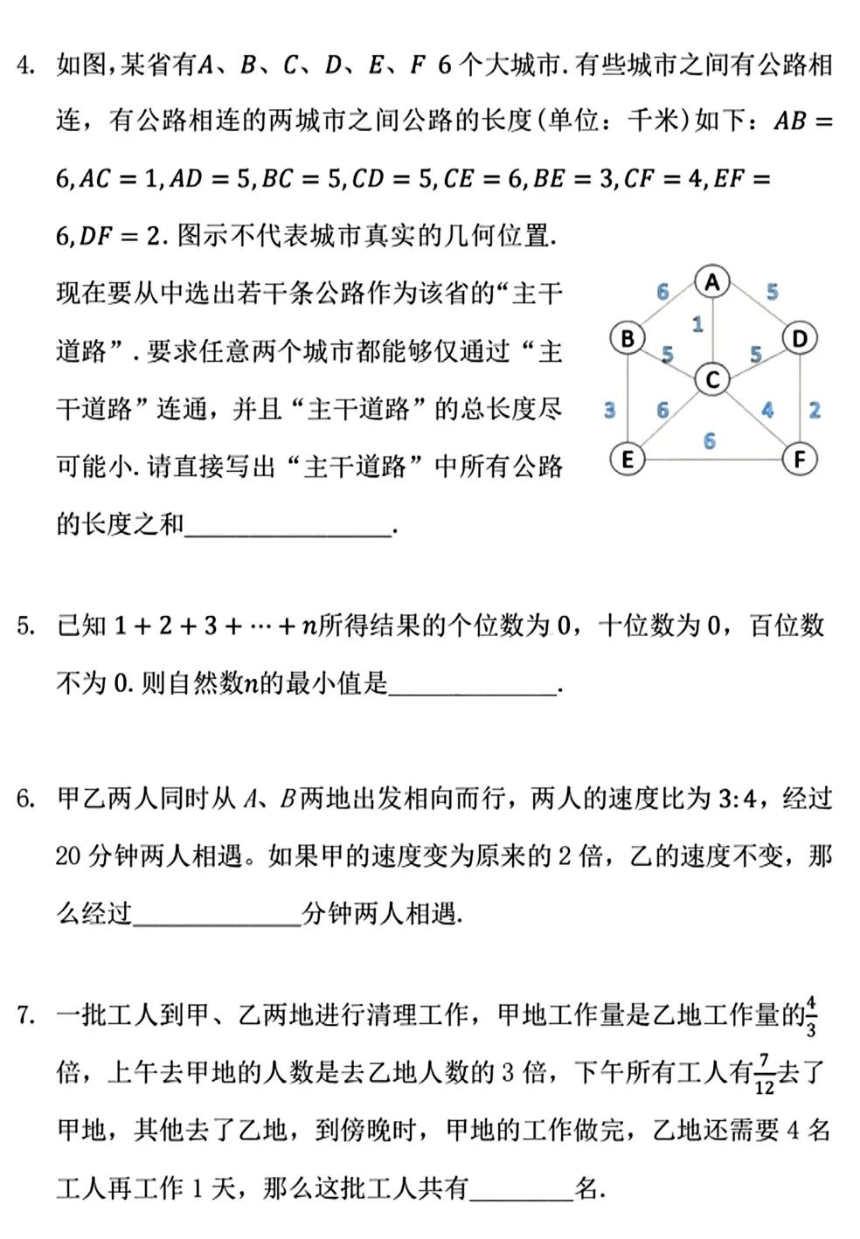
4.如图,某省有A、B、C、D、E、F6个大城市.有些城市之间有公路相
连,有公路相连的两城市之间公路的长度(单位:千米)如下:AB=
6,AC=1,AD=5,BC=5,CD=5,CE=6,BE=3,CF=4,EF=
6,DF=2.图示不代表城市真实的几何位置.
现在要从中选出若干条公路作为该省的“主干
道路”.要求任意两个城市都能够仅通过“主
B
干道路”连通,并且“主干道路”的总长度尽
可能小.请直接写出“主干道路”中所有公路
的长度之和
5.已知1+2+3+…+n所得结果的个位数为0,十位数为0,百位数
不为0.则自然数n的最小值是
6.甲乙两人同时从A、B两地出发相向而行,两人的速度比为3:4,经过
20分钟两人相遇。如果甲的速度变为原来的2倍,乙的速度不变,那
么经过
分钟两人相遇
7.一批工人到甲、乙两地进行清理工作,甲地工作量是乙地工作量的
倍,上午去甲地的人数是去乙地人数的3倍,下午所有工人有2去了
甲地,其他去了乙地,到傍晚时,甲地的工作做完,乙地还需要4名
工人再工作1天,那么这批工人共有
名.
8.一个六位数的末位数字是7,如果把7移到首位,新数就是原数的4倍,则
这个六位数是
9.甲、乙、丙三人以擂台赛形式进行乒乓球训练,每局2人进行比赛,另1人
当裁判.每一局的输方去当下一局的裁判,而由原来的裁判和胜者比赛.某日
训练结束时,发现甲共打了34局,乙共打了45局,丙共当裁判10局,则
该日第5局当裁判的是
10.小明和小红用整数0,1,2,…,n做游戏,这里n是一个大于2024的固定的偶数.
他们轮流做游戏,小明先开始.首先,小明从整数0,1,2,…,n中任意选择一个
整数,接下来轮流选择整数,其选择的这个整数必须要和之前所有已经选过
的整数都不相邻.若有人无法选出这样的数,则该人就输了.若两人都使用
最佳策略,则
会赢得这场游戏.
(2025年2月22日时长90分钟)
题号
2
3
4
5
6
7
P
10
总成绩
得分
其
评阅人
填空题(共十题,每题10分,共100分)
p
1.用若干个长为5厘米,宽为4厘米的长方形纸板拼成的最小正方形的面积是
平方厘米.
2.设1×2×3×…×2024=35n×A,其中n与A为自然数,那么n的最大值是
製
舞
3.标有A、B、C、D、E、F、G记号的七盏灯顺次排成一行,每盏灯安装一个
开关,现在A、B、C三盏灯亮着,其余四盏灯是灭的.小明先拉一下A的开关,
然后拉B、C…直到G的开关各一次,之后再按A到G的顺序拉动开关,并以
此循环.他拉动了2024次后,标有
记号的灯此时是亮的.(写
出全部亮着的灯的标号)
4.如图,某省有A、B、C、D、E、F6个大城市.有些城市之间有公路相
连,有公路相连的两城市之间公路的长度(单位:千米)如下:AB=
6,AC=1,AD=5,BC=5,CD=5,CE=6,BE=3,CF=4,EF=
6,DF=2.图示不代表城市真实的几何位置.
现在要从中选出若干条公路作为该省的“主干
道路”.要求任意两个城市都能够仅通过“主
B
干道路”连通,并且“主干道路”的总长度尽
可能小.请直接写出“主干道路”中所有公路
的长度之和
5.已知1+2+3+…+n所得结果的个位数为0,十位数为0,百位数
不为0.则自然数n的最小值是
6.甲乙两人同时从A、B两地出发相向而行,两人的速度比为3:4,经过
20分钟两人相遇。如果甲的速度变为原来的2倍,乙的速度不变,那
么经过
分钟两人相遇
7.一批工人到甲、乙两地进行清理工作,甲地工作量是乙地工作量的
倍,上午去甲地的人数是去乙地人数的3倍,下午所有工人有2去了
甲地,其他去了乙地,到傍晚时,甲地的工作做完,乙地还需要4名
工人再工作1天,那么这批工人共有
名.
8.一个六位数的末位数字是7,如果把7移到首位,新数就是原数的4倍,则
这个六位数是
9.甲、乙、丙三人以擂台赛形式进行乒乓球训练,每局2人进行比赛,另1人
当裁判.每一局的输方去当下一局的裁判,而由原来的裁判和胜者比赛.某日
训练结束时,发现甲共打了34局,乙共打了45局,丙共当裁判10局,则
该日第5局当裁判的是
10.小明和小红用整数0,1,2,…,n做游戏,这里n是一个大于2024的固定的偶数.
他们轮流做游戏,小明先开始.首先,小明从整数0,1,2,…,n中任意选择一个
整数,接下来轮流选择整数,其选择的这个整数必须要和之前所有已经选过
的整数都不相邻.若有人无法选出这样的数,则该人就输了.若两人都使用
最佳策略,则
会赢得这场游戏.
同课章节目录
