沪科版八年级数学上册12.2.一次函数教案(表格式)
文档属性
| 名称 | 沪科版八年级数学上册12.2.一次函数教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 00:00:00 | ||
图片预览


文档简介
课题: 12.2.一次函数
教 学 设 计 一次函数及其图象和性质是本节的主要内容.教科书采用从特殊到一般的方法,先研究正比例函数的图象与性质然后利用平移知识推得一次函数的图象,仍然以图象直观的方法研究了一次函数的性质(它的截距及增减性).接着,学习用待定系数法确定一次函数的表达式.本节最后介绍了分段函数.这样安排,比较自然,便于教与学.在本章后面,综合与实践中安排了一个用一次函数模拟数据的例子,这不仅说明待定系数法的作用,更重要的是让学生体会到一次函数的一个实实在在的应用. 【学情分析】 学生小学学过正比例关系,知道,数系扩充后,、皆为正数的限制已取消了.在此基础上,学生通过多个函数解析式,引入正比例函数、一次函数形式,并经历画图、观察、比较、猜想、归纳等实践活动,感悟一次函数的图象和性质. 【教学目标】 1.使学生理解一次函数和正比例函数的概念,掌握一次函数及正比例函数的图象与性质;正确地画出一次函数的图象,能从一次函数的图象中获取所需要的信息. 2.能够运用一次函数解决简单的实际问题,并且能够把实际问题中的一次函数关系用表达式或图象表示出来,能够熟练地运用待定系数法求一次函数表达式. 3.通过对一次函数的学习,进一步理解函数的概念,初步掌握学习函数的基本方法,不断发展学生的思维能力和应用数学的能力. 【教学重难点】 教学重点:一次函数及正比例函数的图象与性质 教学难点:一次函数的应用. 【教学准备】 教师准备:制作课件. 学生准备:认真预习教材.
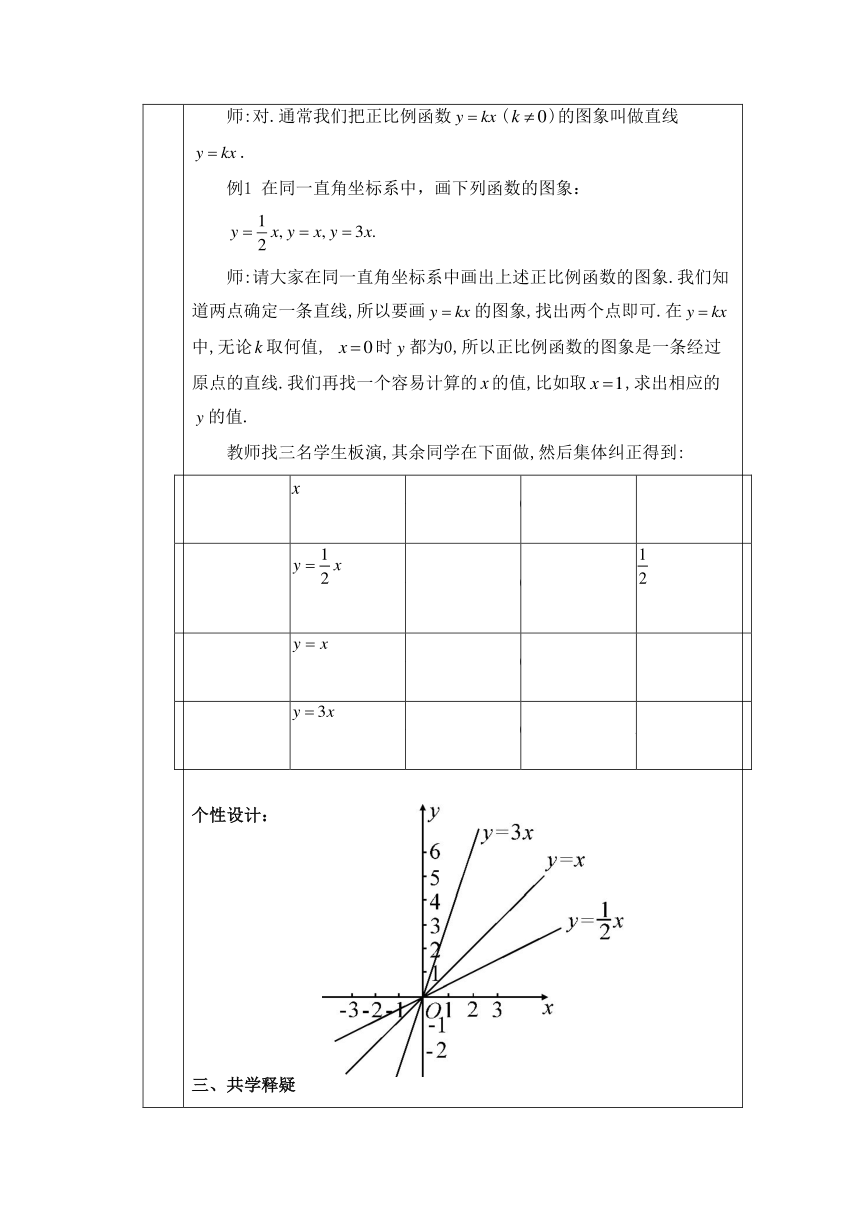
教 学 行 为 一、敏学质疑 教师多媒体出示: 师:观察这些函数,你能发现它们的共同点吗 生:能.它们的自变量的最高次数都是1. 师:很好!不难看出,这些函数都是用自变量的一次式表示的,可以写成的形式.因为它们有这一共同特征,我们把它们归为一类. 教师多媒体出示并口述: 一般地,形如 (、是常数,)的函数,叫做一次函数. 当b=0时,它会是怎样的呢 生:当时,它化简成了. 师:对.我们把有这一特征的函数也归为一类.一般地,形如(、是常数,)的函数,叫做正比例函数. 个性设计: 二、探学辩疑 师:判断下列函数,哪些是一次函数 哪些是正比例函数 (1); (2); (3); (4); (5). 学生讨论后回答,集体纠正. 师:我们现在已经知道了正比例函数的解析式的特点,那么它的图象又有什么特点呢 在前面我们画了、、的图象,它们有什么共同点 生:它们都是一条直线. 师:对.通常我们把正比例函数()的图象叫做直线. 例1 在同一直角坐标系中,画下列函数的图象: 师:请大家在同一直角坐标系中画出上述正比例函数的图象.我们知道两点确定一条直线,所以要画的图象,找出两个点即可.在中,无论取何值, 时都为0,所以正比例函数的图象是一条经过原点的直线.我们再找一个容易计算的的值,比如取,求出相应的的值. 教师找三名学生板演,其余同学在下面做,然后集体纠正得到: …01……0……01……03…
个性设计: 三、共学释疑 师:它们除了都是正比例函数外, 都是大于0的.它们的图象除了是经过原点的直线外,还有什么共同点 生:它们都经过一、三象限. 师:除此之外,随着值的增大,的值是怎样变化的 学生观察后回答:增大. 师:很好!它们还有没有其他的共同之处 学生继续观察,发现另一共同点:它们都是自左向右上升的. 例2 在同一直角坐标系中,画下列函数的图象: 思考:它们有什么共同点? 学生作图后回答. 生甲:它们都是过原点的一条直线. 生乙:它们都经过二、四象限. 生丙: 的值随着的增大而减小. 生丁:它们都是自左向右下降的. 师:同学们回答得很好!我们由这两个例子得到如下结论: 在正比例函数中,当时,随的增大而增大,图象经过一、三象限;当时,随的增大而减小,图象经过二、四象限. 师:那么大家将前面的三个图象结合起来,看的大小对的图象有什么影响 生:越大,图象越接近轴;越小,图象越接近轴. 师:很好,大家观察得很仔细. 个性设计:
课堂 生成 师:它们除了都是正比例函数外, 都是大于0的.它们的图象除了是经过原点的直线外,还有什么共同点 生:它们都经过一、三象限. 师:除此之外,随着值的增大,的值是怎样变化的 学生观察后回答:增大. 师:很好!它们还有没有其他的共同之处 学生继续观察,发现另一共同点:它们都是自左向右上升的. 例2 在同一直角坐标系中,画下列函数的图象: 思考:它们有什么共同点? 学生作图后回答. 生甲:它们都是过原点的一条直线. 生乙:它们都经过二、四象限. 生丙: 的值随着的增大而减小. 生丁:它们都是自左向右下降的. 师:同学们回答得很好!我们由这两个例子得到如下结论: 在正比例函数中,当时,随的增大而增大,图象经过一、三象限;当时,随的增大而减小,图象经过二、四象限. 师:那么大家将前面的三个图象结合起来,看的大小对的图象有什么影响 生:越大,图象越接近轴;越小,图象越接近轴. 师:很好,大家观察得很仔细. 个性设计:
教学 效果 学生掌握一次函数的定义 ,会判断是否是一次函数,加深了对函数的理解。 理解正比例函数的特点,了解一次函数和正比例函数的联系和区别。 通过画图了解函数图像的含义,体会了数形结合思想。
教学反思:
在讲《一次函数》章节时,我深刻体会到了数学教育的魅力与挑战,以及它对学生逻辑思维和问题解决能力的培养所起到的关键作用。以下是我对这一章节教学的一些感悟:
一、理论与实践的结合是关键
一次函数的学习不仅仅是公式和图像的堆砌,更重要的是理解其背后的实际意义。在教学过程中,我尝试将抽象的数学概念与学生的日常生活联系起来,比如通过购物、旅行等实际情境引入一次函数的概念,让学生理解y=kx+b这个公式是如何描述生活中变量之间关系的。这样的教学方式不仅增强了学生的学习兴趣,还帮助他们更好地理解了函数的本质。
二、图像教学的力量
一次函数的图像是理解其性质的重要工具。我利用多媒体课件和实物投影仪,直观地展示了不同斜率k和截距b下函数的图像变化,让学生通过观察、讨论和动手操作,深刻理解了斜率决定函数图像的增减性和方向,截距则决定了函数图像与y轴的交点位置。这种图像化的教学方式极大地提高了学生的空间想象能力和抽象思维能力。
三、小组合作与自主探究
小组合作学习在这次教学中发挥了重要作用。我鼓励学生分组讨论,共同解决问题,这不仅促进了学生之间的交流与合作,还让他们在相互帮助中发现了彼此的优点和不足,从而实现了共同进步。同时,我也鼓励学生在课后进行自主探究,通过观察生活中的一次函数现象,尝试自己建立函数模型,这种学习方式极大地激发了学生的探索精神和创新能力。
四、反思与调整
在教学过程中,我也遇到了不少挑战,比如如何平衡不同水平学生的需求,如何更有效地解释抽象概念等。通过反思和调整教学策略,我逐渐找到了更适合学生的教学方法,比如通过分层教学来满足不同学生的需求,通过引入更多生活实例来解释抽象概念等。这些调整不仅提高了教学效果,也让我更加深刻地理解了“因材施教”的重要性。
五、数学与生活的紧密联系
通过这次教学,我更加深刻地体会到了数学与生活的紧密联系。一次函数不仅是一个数学工具,更是我们理解和描述世界的一种语言。它教会我们如何从数据中提取信息,如何预测未来趋势,如何做出更明智的决策。这种能力的培养对学生未来的学习和生活都将产生深远的影响。
总之,《一次函数》这一章节让我深刻体会到了数学教育的魅力和挑战,也让我更加坚定了以学生为中心、注重实践与理论相结合的教学理念。我相信,在未来的教学中,我会继续探索更多有效的教学方法,为学生的数学学习和全面发展贡献自己的力量。
教 学 设 计 一次函数及其图象和性质是本节的主要内容.教科书采用从特殊到一般的方法,先研究正比例函数的图象与性质然后利用平移知识推得一次函数的图象,仍然以图象直观的方法研究了一次函数的性质(它的截距及增减性).接着,学习用待定系数法确定一次函数的表达式.本节最后介绍了分段函数.这样安排,比较自然,便于教与学.在本章后面,综合与实践中安排了一个用一次函数模拟数据的例子,这不仅说明待定系数法的作用,更重要的是让学生体会到一次函数的一个实实在在的应用. 【学情分析】 学生小学学过正比例关系,知道,数系扩充后,、皆为正数的限制已取消了.在此基础上,学生通过多个函数解析式,引入正比例函数、一次函数形式,并经历画图、观察、比较、猜想、归纳等实践活动,感悟一次函数的图象和性质. 【教学目标】 1.使学生理解一次函数和正比例函数的概念,掌握一次函数及正比例函数的图象与性质;正确地画出一次函数的图象,能从一次函数的图象中获取所需要的信息. 2.能够运用一次函数解决简单的实际问题,并且能够把实际问题中的一次函数关系用表达式或图象表示出来,能够熟练地运用待定系数法求一次函数表达式. 3.通过对一次函数的学习,进一步理解函数的概念,初步掌握学习函数的基本方法,不断发展学生的思维能力和应用数学的能力. 【教学重难点】 教学重点:一次函数及正比例函数的图象与性质 教学难点:一次函数的应用. 【教学准备】 教师准备:制作课件. 学生准备:认真预习教材.
教 学 行 为 一、敏学质疑 教师多媒体出示: 师:观察这些函数,你能发现它们的共同点吗 生:能.它们的自变量的最高次数都是1. 师:很好!不难看出,这些函数都是用自变量的一次式表示的,可以写成的形式.因为它们有这一共同特征,我们把它们归为一类. 教师多媒体出示并口述: 一般地,形如 (、是常数,)的函数,叫做一次函数. 当b=0时,它会是怎样的呢 生:当时,它化简成了. 师:对.我们把有这一特征的函数也归为一类.一般地,形如(、是常数,)的函数,叫做正比例函数. 个性设计: 二、探学辩疑 师:判断下列函数,哪些是一次函数 哪些是正比例函数 (1); (2); (3); (4); (5). 学生讨论后回答,集体纠正. 师:我们现在已经知道了正比例函数的解析式的特点,那么它的图象又有什么特点呢 在前面我们画了、、的图象,它们有什么共同点 生:它们都是一条直线. 师:对.通常我们把正比例函数()的图象叫做直线. 例1 在同一直角坐标系中,画下列函数的图象: 师:请大家在同一直角坐标系中画出上述正比例函数的图象.我们知道两点确定一条直线,所以要画的图象,找出两个点即可.在中,无论取何值, 时都为0,所以正比例函数的图象是一条经过原点的直线.我们再找一个容易计算的的值,比如取,求出相应的的值. 教师找三名学生板演,其余同学在下面做,然后集体纠正得到: …01……0……01……03…
个性设计: 三、共学释疑 师:它们除了都是正比例函数外, 都是大于0的.它们的图象除了是经过原点的直线外,还有什么共同点 生:它们都经过一、三象限. 师:除此之外,随着值的增大,的值是怎样变化的 学生观察后回答:增大. 师:很好!它们还有没有其他的共同之处 学生继续观察,发现另一共同点:它们都是自左向右上升的. 例2 在同一直角坐标系中,画下列函数的图象: 思考:它们有什么共同点? 学生作图后回答. 生甲:它们都是过原点的一条直线. 生乙:它们都经过二、四象限. 生丙: 的值随着的增大而减小. 生丁:它们都是自左向右下降的. 师:同学们回答得很好!我们由这两个例子得到如下结论: 在正比例函数中,当时,随的增大而增大,图象经过一、三象限;当时,随的增大而减小,图象经过二、四象限. 师:那么大家将前面的三个图象结合起来,看的大小对的图象有什么影响 生:越大,图象越接近轴;越小,图象越接近轴. 师:很好,大家观察得很仔细. 个性设计:
课堂 生成 师:它们除了都是正比例函数外, 都是大于0的.它们的图象除了是经过原点的直线外,还有什么共同点 生:它们都经过一、三象限. 师:除此之外,随着值的增大,的值是怎样变化的 学生观察后回答:增大. 师:很好!它们还有没有其他的共同之处 学生继续观察,发现另一共同点:它们都是自左向右上升的. 例2 在同一直角坐标系中,画下列函数的图象: 思考:它们有什么共同点? 学生作图后回答. 生甲:它们都是过原点的一条直线. 生乙:它们都经过二、四象限. 生丙: 的值随着的增大而减小. 生丁:它们都是自左向右下降的. 师:同学们回答得很好!我们由这两个例子得到如下结论: 在正比例函数中,当时,随的增大而增大,图象经过一、三象限;当时,随的增大而减小,图象经过二、四象限. 师:那么大家将前面的三个图象结合起来,看的大小对的图象有什么影响 生:越大,图象越接近轴;越小,图象越接近轴. 师:很好,大家观察得很仔细. 个性设计:
教学 效果 学生掌握一次函数的定义 ,会判断是否是一次函数,加深了对函数的理解。 理解正比例函数的特点,了解一次函数和正比例函数的联系和区别。 通过画图了解函数图像的含义,体会了数形结合思想。
教学反思:
在讲《一次函数》章节时,我深刻体会到了数学教育的魅力与挑战,以及它对学生逻辑思维和问题解决能力的培养所起到的关键作用。以下是我对这一章节教学的一些感悟:
一、理论与实践的结合是关键
一次函数的学习不仅仅是公式和图像的堆砌,更重要的是理解其背后的实际意义。在教学过程中,我尝试将抽象的数学概念与学生的日常生活联系起来,比如通过购物、旅行等实际情境引入一次函数的概念,让学生理解y=kx+b这个公式是如何描述生活中变量之间关系的。这样的教学方式不仅增强了学生的学习兴趣,还帮助他们更好地理解了函数的本质。
二、图像教学的力量
一次函数的图像是理解其性质的重要工具。我利用多媒体课件和实物投影仪,直观地展示了不同斜率k和截距b下函数的图像变化,让学生通过观察、讨论和动手操作,深刻理解了斜率决定函数图像的增减性和方向,截距则决定了函数图像与y轴的交点位置。这种图像化的教学方式极大地提高了学生的空间想象能力和抽象思维能力。
三、小组合作与自主探究
小组合作学习在这次教学中发挥了重要作用。我鼓励学生分组讨论,共同解决问题,这不仅促进了学生之间的交流与合作,还让他们在相互帮助中发现了彼此的优点和不足,从而实现了共同进步。同时,我也鼓励学生在课后进行自主探究,通过观察生活中的一次函数现象,尝试自己建立函数模型,这种学习方式极大地激发了学生的探索精神和创新能力。
四、反思与调整
在教学过程中,我也遇到了不少挑战,比如如何平衡不同水平学生的需求,如何更有效地解释抽象概念等。通过反思和调整教学策略,我逐渐找到了更适合学生的教学方法,比如通过分层教学来满足不同学生的需求,通过引入更多生活实例来解释抽象概念等。这些调整不仅提高了教学效果,也让我更加深刻地理解了“因材施教”的重要性。
五、数学与生活的紧密联系
通过这次教学,我更加深刻地体会到了数学与生活的紧密联系。一次函数不仅是一个数学工具,更是我们理解和描述世界的一种语言。它教会我们如何从数据中提取信息,如何预测未来趋势,如何做出更明智的决策。这种能力的培养对学生未来的学习和生活都将产生深远的影响。
总之,《一次函数》这一章节让我深刻体会到了数学教育的魅力和挑战,也让我更加坚定了以学生为中心、注重实践与理论相结合的教学理念。我相信,在未来的教学中,我会继续探索更多有效的教学方法,为学生的数学学习和全面发展贡献自己的力量。
