2024-2025学年陕西省西安八十五中八年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年陕西省西安八十五中八年级(下)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 695.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 20:12:52 | ||
图片预览




文档简介
2024-2025学年陕西省西安八十五中八年级(下)期末数学试卷
一、选择题(共8小题,每小题3分,计24分。每小题只有一个选项是符合题意的)
1.(3分)剪纸是中国首批国家级非物质文化遗产,在如图所示的四个剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)已知x>y,下列不等式成立的是( )
A.﹣x>﹣y B.x+2<y+2 C.x﹣5<y﹣5 D.
3.(3分)若分式的值为0,则x的值为( )
A.2 B.﹣2 C.±2 D.4
4.(3分)下列从左到右的变形中,属于因式分解的是( )
A.x2﹣12x+36=(x﹣6)2
B.x2﹣4=(x+4)(x﹣4)
C.x(x﹣y)=x2﹣xy
D.x2﹣y2+1=(x+y)(x﹣y)+1
5.(3分)使不等式5x+1<2x+4成立的最大整数解是( )
A.﹣1 B.0
C.1 D.以上都不对
6.(3分)如图,四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠FPE=120°,则∠PFE的度数是( )
A.45° B.40° C.30° D.60°
7.(3分)已知a,b,c为△ABC的三边,满足a2﹣b2+ac﹣bc=0,则△ABC的形状是( )
A.直角三角形
B.等腰直角三角形
C.等腰三角形或直角三角形
D.等腰三角形
8.(3分)如图,在正方形ABCD中,∠DAC的平分线交DC于点E,点P,Q分别是AD,AE上的动点,若DQ+PQ的最小值是2,则正方形ABCD的边长为( )
A.1 B. C.2 D.
二、填空题(共6小题,每小题3分,计18分)
9.(3分)分解因式:x3﹣6x2+9x= .
10.(3分)一个多边形的内角和比四边形内角和的2倍多180°,这个多边形的边数是 .
11.(3分)计算: .
12.(3分)如图,将△ABC绕点B顺时针旋转100°,得到△EBD,若点E恰好在AC的延长线上,则∠CED的度数为 .
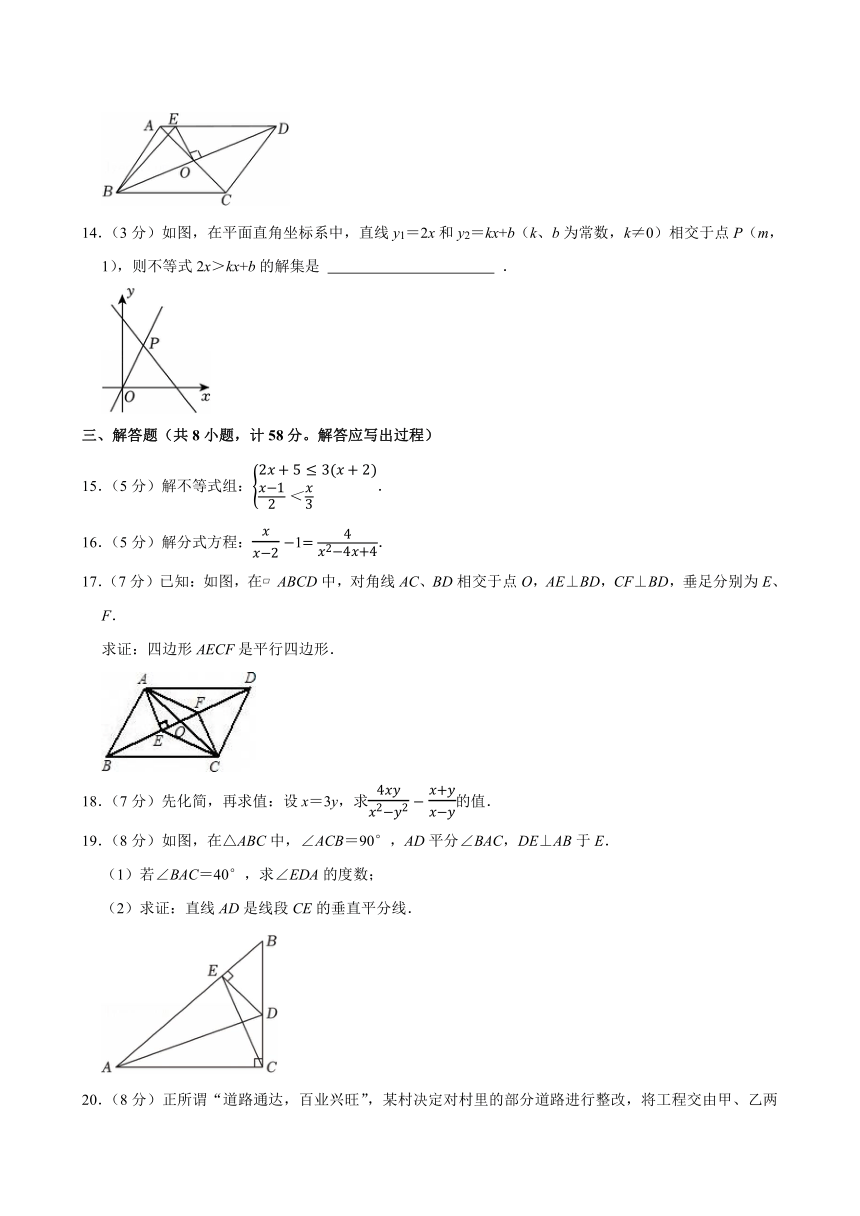
13.(3分)如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若△ABE的周长为15,则 ABCD的周长为 .
14.(3分)如图,在平面直角坐标系中,直线y1=2x和y2=kx+b(k、b为常数,k≠0)相交于点P(m,1),则不等式2x>kx+b的解集是 .
三、解答题(共8小题,计58分。解答应写出过程)
15.(5分)解不等式组:.
16.(5分)解分式方程:1.
17.(7分)已知:如图,在 ABCD中,对角线AC、BD相交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:四边形AECF是平行四边形.
18.(7分)先化简,再求值:设x=3y,求的值.
19.(8分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=40°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
20.(8分)正所谓“道路通达,百业兴旺”,某村决定对村里的部分道路进行整改,将工程交由甲、乙两个工程队来完成.已知甲工程队每天比乙工程队多修0.4km,如果甲工程队修6.4km所用的天数是乙工程队修9.6km所用天数的一半.
(1)求甲,乙两个工程队每天各修路多少km?
(2)现计划再修建长度为24km的道路,由甲、乙两个工程队来完成.若甲队每天所需费用为2.4万元,乙队每天所需费用为1.5万元,求在总费用不超过33.6万元的情况下,至少安排乙工程队施工多少天?
21.(8分)如图,已知直线y1=kx+b经过点A(﹣6,0),B(﹣1,5),直线y2=﹣2x+a与直线AB相交于点M,与x轴交于点D,点M的横坐标为﹣3.
(1)根据图象,直接写出当kx+b<﹣2x+a时,x的取值范围是什么?
(2)求直线AB的表达式和a的值;
(3)若点P在直线AB上,且S△ADP=9,求点P的坐标.
22.(10分)探究,如图1所示,平行四边形ABCD中,AC与BD交于点O,过点O的直线分别交AD,BC于点E,F.
(1)求证:OE=OF;
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将平行四边形ABCD的面积分成二等份?试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图2所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请帮助张大爷把地分开.
2024-2025学年陕西省西安八十五中八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C D A A B C D D
一、选择题(共8小题,每小题3分,计24分。每小题只有一个选项是符合题意的)
1.(3分)剪纸是中国首批国家级非物质文化遗产,在如图所示的四个剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A、既不是轴对称图形,也不是中心对称图形,不符合题意;
B、是轴对称图形,不是中心对称图形,不符合题意;
C、既是轴对称图形又是中心对称图形,符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意;
故选:C.
2.(3分)已知x>y,下列不等式成立的是( )
A.﹣x>﹣y B.x+2<y+2 C.x﹣5<y﹣5 D.
【解答】解:已知x>y,
两边同时乘以﹣1得﹣x<﹣y,则A不符合题意,
两边同时加上2得x+2>y+2,则B不符合题意,
两边同时减去5得x﹣5>y﹣5,则C不符合题意,
两边同时除以3得,则D符合题意,
故选:D.
3.(3分)若分式的值为0,则x的值为( )
A.2 B.﹣2 C.±2 D.4
【解答】解:要使分式由分子x2﹣4=0,解得:x=±2.
而x=2时,分母x+2=2+2=4≠0;
x=﹣2时分母x+2=0,分式没有意义.
所以x=2.故选:A.
4.(3分)下列从左到右的变形中,属于因式分解的是( )
A.x2﹣12x+36=(x﹣6)2
B.x2﹣4=(x+4)(x﹣4)
C.x(x﹣y)=x2﹣xy
D.x2﹣y2+1=(x+y)(x﹣y)+1
【解答】解:x2﹣12x+36=(x﹣6)2符合因式分解的定义,则A符合题意,
x2﹣4=(x+2)(x﹣2),则B不符合题意,
x(x﹣y)=x2﹣xy是乘法运算,则C不符合题意,
x2﹣y2+1=(x+y)(x﹣y)+1中等号右边不是积的形式,则D不符合题意,
故选:A.
5.(3分)使不等式5x+1<2x+4成立的最大整数解是( )
A.﹣1 B.0
C.1 D.以上都不对
【解答】解:5x+1<2x+4,
5x﹣2x<﹣1+4,
3x<3,
∴x<1,
则不等式的最大整数解为0,
故选:B.
6.(3分)如图,四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠FPE=120°,则∠PFE的度数是( )
A.45° B.40° C.30° D.60°
【解答】解:∵E,P分别是AB,BD的中点,
∴EP为△ABD的中位线,
∴EPAD,
同理可得:FPBC,
∵AD=BC,
∴EP=FP,
∵∠FPE=120°,
∴∠PFE=∠PEF(180°﹣120°)=30°,
故选:C.
7.(3分)已知a,b,c为△ABC的三边,满足a2﹣b2+ac﹣bc=0,则△ABC的形状是( )
A.直角三角形
B.等腰直角三角形
C.等腰三角形或直角三角形
D.等腰三角形
【解答】解:因为a,b,c为△ABC的三边,
所以a>0,b>0,c>0,
因为a2﹣b2+ac﹣bc=0,
所以a2﹣b2+ac﹣bc
=(a+b)(a﹣b)+c(a﹣b)
=(a﹣b)(a+b+c)
=0,
因为a>0,b>0,c>0,
所以a+b+c>0,
所以a﹣b=0,
所以a=b,
所以△ABC的形状是等腰三角形.
故选:D.
8.(3分)如图,在正方形ABCD中,∠DAC的平分线交DC于点E,点P,Q分别是AD,AE上的动点,若DQ+PQ的最小值是2,则正方形ABCD的边长为( )
A.1 B. C.2 D.
【解答】解:过D作DF⊥AE于F,延长DF交AC于D′,过D′作D′P′⊥AD于P′,D′P′交AE于Q′.
∵DD′⊥AE于F,
∴∠AFD=∠AFD′=90°,
∵∠DAC的平分线交DC于点E,
∴∠DAE=∠CAE,
∵在△DAF与△D′AF中,
,
∴△DAF≌△D′AF(ASA),
∴D′是D关于AE的对称点,AD=AD′,
∴D′P′即为DQ+PQ的最小值.
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′=2,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=8,
∴AD′=2,AD=AD′=2,
∴正方形ABCD的边长为2,
故选:D.
二、填空题(共6小题,每小题3分,计18分)
9.(3分)分解因式:x3﹣6x2+9x= x(x﹣3)2 .
【解答】解:x3﹣6x2+9x
=x(x2﹣6x+9)
=x(x﹣3)2,
故答案为:x(x﹣3)2.
10.(3分)一个多边形的内角和比四边形内角和的2倍多180°,这个多边形的边数是 7 .
【解答】解:∵四边形内角和为360°,
∴这个多边形内角和为360°×2+180°=900°,
∵多边形内角和为(n﹣2)×180°,
∴(n﹣2)×180°=900°,
∴n=7,
∴这个多边形的边数为:7,
故答案为:7.
11.(3分)计算: .
【解答】解:原式
,
故答案为:.
12.(3分)如图,将△ABC绕点B顺时针旋转100°,得到△EBD,若点E恰好在AC的延长线上,则∠CED的度数为 80° .
【解答】解:由题意得,△ABC≌△EBD,∠ABE=100°,
∴∠A=∠BED,AB=BE,
∴∠A=∠BEC,
∴∠CED=∠BEC+∠BED=80°,
故答案为:80°.
13.(3分)如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若△ABE的周长为15,则 ABCD的周长为 30 .
【解答】解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵△ABE的周长为15,
∴AB+BE+AE=15,
∵OE⊥BD,
∴OE是线段BD的垂直平分线,
∴BE=ED,
∴AB+BE+AE=AB+AD=15,
∴ ABCD的周长=2(AB+AD)=2×15=30,
故答案为:30.
14.(3分)如图,在平面直角坐标系中,直线y1=2x和y2=kx+b(k、b为常数,k≠0)相交于点P(m,1),则不等式2x>kx+b的解集是 x .
【解答】解:将点P(m,1)代入y=2x,
得2m=1,
解得m,
∴P(,1),
根据图象,不等2x>kx+b的解集为x,
故答案为:x.
三、解答题(共8小题,计58分。解答应写出过程)
15.(5分)解不等式组:.
【解答】解:解第一个不等式去括号得2x+5≤3x+6,解得x≥﹣1;
解第二个不等式去分母得3x﹣3<2x,解得x<3;
∴不等式组的解集是﹣1≤x<3.
16.(5分)解分式方程:1.
【解答】解:1,
方程两边乘(x﹣2)2得:x(x﹣2)﹣(x﹣2)2=4,
解得:x=4,
检验:当x=4时,(x﹣2)2≠0.
所以原方程的解为x=4.
17.(7分)已知:如图,在 ABCD中,对角线AC、BD相交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:四边形AECF是平行四边形.
【解答】证明:在平行四边形ABCD中,
∵AE,CF分别为△ABD与△BCD的高,
∴AE=CF,
∵AE⊥BD,CF⊥BD,∴AE∥CF,
∴四边形AECF是平行四边形.
18.(7分)先化简,再求值:设x=3y,求的值.
【解答】解:
,
∵x=3y,
∴原式.
19.(8分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=40°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
【解答】(1)解:∵∠BAC=40°,AD平分∠BAC,
∴∠EAD∠BAC=20°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣20°=70°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
在△AED和△ACD中,
,
∴△AED≌△ACD(AAS),
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,AD平分线段EC,
即直线AD是线段CE的垂直平分线.
20.(8分)正所谓“道路通达,百业兴旺”,某村决定对村里的部分道路进行整改,将工程交由甲、乙两个工程队来完成.已知甲工程队每天比乙工程队多修0.4km,如果甲工程队修6.4km所用的天数是乙工程队修9.6km所用天数的一半.
(1)求甲,乙两个工程队每天各修路多少km?
(2)现计划再修建长度为24km的道路,由甲、乙两个工程队来完成.若甲队每天所需费用为2.4万元,乙队每天所需费用为1.5万元,求在总费用不超过33.6万元的情况下,至少安排乙工程队施工多少天?
【解答】解:(1)设乙工程队每天修路x km,则甲工程队每天修路(x+0.4)km,
根据题意得:,
解得:x=1.2,
经检验,x=1.2是所列方程的解,且符合题意,
∴x+0.4=1.2+0.4=1.6.
答:甲工程队每天修路1.6km,乙工程队每天修路1.2km;
(2)设安排乙工程队施工m天,则安排甲工程队施工天,
根据题意得:2.41.5m≤33.6,
解得:m≥8,
∴m的最小值为8.
答:至少安排乙工程队施工8天.
21.(8分)如图,已知直线y1=kx+b经过点A(﹣6,0),B(﹣1,5),直线y2=﹣2x+a与直线AB相交于点M,与x轴交于点D,点M的横坐标为﹣3.
(1)根据图象,直接写出当kx+b<﹣2x+a时,x的取值范围是什么?
(2)求直线AB的表达式和a的值;
(3)若点P在直线AB上,且S△ADP=9,求点P的坐标.
【解答】解:(1)由图象可知,当kx+b<﹣2x+a时,
x的取值范围为x<﹣3;
(2)由条件可得,
解得,
∴直线AB的表达式为y1=x+6,
把x=﹣3代入y1=x+6,
得y=3,
∴点M的坐标为(﹣3,3),
把(﹣3,3)代入y2=﹣2x+a,
得a=﹣3.
(3)设P(m,m+6),
把y=0代入y2=﹣2x﹣3得,x,
∴D(,0),
∵A(﹣6,0),
∴AD,
∴S△ADPAD |yP|=9,
∴|m+6|=9,
解得m=﹣2或﹣10.
∴P(﹣2,4)或(﹣10,﹣4).
22.(10分)探究,如图1所示,平行四边形ABCD中,AC与BD交于点O,过点O的直线分别交AD,BC于点E,F.
(1)求证:OE=OF;
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将平行四边形ABCD的面积分成二等份?试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图2所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请帮助张大爷把地分开.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,
∴∠EDO=∠FBO,
在△EDO和△FBO中,
,
∴△EDO≌△FBO(ASA),
∴OE=OF;
(2)由(1)知:△EDO≌△FBO,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△EAO和△FCO中,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴AE+BF=CF+DE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AE+BF+AB+EF=CF+DE+CD+EF,
即四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是将平行四边形ABCD的面积分成二等份,理由如下:
∵四边形ABCD是平行四边形,
∴OD=OB,OC=OA,
在△DOC和△BOA中,
,
∴△DOC≌△BOA(SAS),
∴S△DOC=S△BOA,
∵△EDO≌△FBO,△AOE≌△COF,
∴S△EDO=S△FBO,S△AOE=S△COF,
∴S△DOC+S△EDO+S△COF=S△BOA+S△FBO+S△AOE,
即四边形AEFB与四边形DEFC的面积相等,
∴直线EF是将平行四边形ABCD的面积分成二等份,
应用:连接AC、BD交于O,作直线OP交CD、AB于E、F,如图:
由(2)(3)可知,四边形AFED和四边形BFEC的周长和面积均相等,
∴把平行四边形的菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,则图中EF把平行四边形分成的两部分,符合题意.
一、选择题(共8小题,每小题3分,计24分。每小题只有一个选项是符合题意的)
1.(3分)剪纸是中国首批国家级非物质文化遗产,在如图所示的四个剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(3分)已知x>y,下列不等式成立的是( )
A.﹣x>﹣y B.x+2<y+2 C.x﹣5<y﹣5 D.
3.(3分)若分式的值为0,则x的值为( )
A.2 B.﹣2 C.±2 D.4
4.(3分)下列从左到右的变形中,属于因式分解的是( )
A.x2﹣12x+36=(x﹣6)2
B.x2﹣4=(x+4)(x﹣4)
C.x(x﹣y)=x2﹣xy
D.x2﹣y2+1=(x+y)(x﹣y)+1
5.(3分)使不等式5x+1<2x+4成立的最大整数解是( )
A.﹣1 B.0
C.1 D.以上都不对
6.(3分)如图,四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠FPE=120°,则∠PFE的度数是( )
A.45° B.40° C.30° D.60°
7.(3分)已知a,b,c为△ABC的三边,满足a2﹣b2+ac﹣bc=0,则△ABC的形状是( )
A.直角三角形
B.等腰直角三角形
C.等腰三角形或直角三角形
D.等腰三角形
8.(3分)如图,在正方形ABCD中,∠DAC的平分线交DC于点E,点P,Q分别是AD,AE上的动点,若DQ+PQ的最小值是2,则正方形ABCD的边长为( )
A.1 B. C.2 D.
二、填空题(共6小题,每小题3分,计18分)
9.(3分)分解因式:x3﹣6x2+9x= .
10.(3分)一个多边形的内角和比四边形内角和的2倍多180°,这个多边形的边数是 .
11.(3分)计算: .
12.(3分)如图,将△ABC绕点B顺时针旋转100°,得到△EBD,若点E恰好在AC的延长线上,则∠CED的度数为 .
13.(3分)如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若△ABE的周长为15,则 ABCD的周长为 .
14.(3分)如图,在平面直角坐标系中,直线y1=2x和y2=kx+b(k、b为常数,k≠0)相交于点P(m,1),则不等式2x>kx+b的解集是 .
三、解答题(共8小题,计58分。解答应写出过程)
15.(5分)解不等式组:.
16.(5分)解分式方程:1.
17.(7分)已知:如图,在 ABCD中,对角线AC、BD相交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:四边形AECF是平行四边形.
18.(7分)先化简,再求值:设x=3y,求的值.
19.(8分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=40°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
20.(8分)正所谓“道路通达,百业兴旺”,某村决定对村里的部分道路进行整改,将工程交由甲、乙两个工程队来完成.已知甲工程队每天比乙工程队多修0.4km,如果甲工程队修6.4km所用的天数是乙工程队修9.6km所用天数的一半.
(1)求甲,乙两个工程队每天各修路多少km?
(2)现计划再修建长度为24km的道路,由甲、乙两个工程队来完成.若甲队每天所需费用为2.4万元,乙队每天所需费用为1.5万元,求在总费用不超过33.6万元的情况下,至少安排乙工程队施工多少天?
21.(8分)如图,已知直线y1=kx+b经过点A(﹣6,0),B(﹣1,5),直线y2=﹣2x+a与直线AB相交于点M,与x轴交于点D,点M的横坐标为﹣3.
(1)根据图象,直接写出当kx+b<﹣2x+a时,x的取值范围是什么?
(2)求直线AB的表达式和a的值;
(3)若点P在直线AB上,且S△ADP=9,求点P的坐标.
22.(10分)探究,如图1所示,平行四边形ABCD中,AC与BD交于点O,过点O的直线分别交AD,BC于点E,F.
(1)求证:OE=OF;
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将平行四边形ABCD的面积分成二等份?试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图2所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请帮助张大爷把地分开.
2024-2025学年陕西省西安八十五中八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C D A A B C D D
一、选择题(共8小题,每小题3分,计24分。每小题只有一个选项是符合题意的)
1.(3分)剪纸是中国首批国家级非物质文化遗产,在如图所示的四个剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A、既不是轴对称图形,也不是中心对称图形,不符合题意;
B、是轴对称图形,不是中心对称图形,不符合题意;
C、既是轴对称图形又是中心对称图形,符合题意;
D、不是轴对称图形,是中心对称图形,不符合题意;
故选:C.
2.(3分)已知x>y,下列不等式成立的是( )
A.﹣x>﹣y B.x+2<y+2 C.x﹣5<y﹣5 D.
【解答】解:已知x>y,
两边同时乘以﹣1得﹣x<﹣y,则A不符合题意,
两边同时加上2得x+2>y+2,则B不符合题意,
两边同时减去5得x﹣5>y﹣5,则C不符合题意,
两边同时除以3得,则D符合题意,
故选:D.
3.(3分)若分式的值为0,则x的值为( )
A.2 B.﹣2 C.±2 D.4
【解答】解:要使分式由分子x2﹣4=0,解得:x=±2.
而x=2时,分母x+2=2+2=4≠0;
x=﹣2时分母x+2=0,分式没有意义.
所以x=2.故选:A.
4.(3分)下列从左到右的变形中,属于因式分解的是( )
A.x2﹣12x+36=(x﹣6)2
B.x2﹣4=(x+4)(x﹣4)
C.x(x﹣y)=x2﹣xy
D.x2﹣y2+1=(x+y)(x﹣y)+1
【解答】解:x2﹣12x+36=(x﹣6)2符合因式分解的定义,则A符合题意,
x2﹣4=(x+2)(x﹣2),则B不符合题意,
x(x﹣y)=x2﹣xy是乘法运算,则C不符合题意,
x2﹣y2+1=(x+y)(x﹣y)+1中等号右边不是积的形式,则D不符合题意,
故选:A.
5.(3分)使不等式5x+1<2x+4成立的最大整数解是( )
A.﹣1 B.0
C.1 D.以上都不对
【解答】解:5x+1<2x+4,
5x﹣2x<﹣1+4,
3x<3,
∴x<1,
则不等式的最大整数解为0,
故选:B.
6.(3分)如图,四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠FPE=120°,则∠PFE的度数是( )
A.45° B.40° C.30° D.60°
【解答】解:∵E,P分别是AB,BD的中点,
∴EP为△ABD的中位线,
∴EPAD,
同理可得:FPBC,
∵AD=BC,
∴EP=FP,
∵∠FPE=120°,
∴∠PFE=∠PEF(180°﹣120°)=30°,
故选:C.
7.(3分)已知a,b,c为△ABC的三边,满足a2﹣b2+ac﹣bc=0,则△ABC的形状是( )
A.直角三角形
B.等腰直角三角形
C.等腰三角形或直角三角形
D.等腰三角形
【解答】解:因为a,b,c为△ABC的三边,
所以a>0,b>0,c>0,
因为a2﹣b2+ac﹣bc=0,
所以a2﹣b2+ac﹣bc
=(a+b)(a﹣b)+c(a﹣b)
=(a﹣b)(a+b+c)
=0,
因为a>0,b>0,c>0,
所以a+b+c>0,
所以a﹣b=0,
所以a=b,
所以△ABC的形状是等腰三角形.
故选:D.
8.(3分)如图,在正方形ABCD中,∠DAC的平分线交DC于点E,点P,Q分别是AD,AE上的动点,若DQ+PQ的最小值是2,则正方形ABCD的边长为( )
A.1 B. C.2 D.
【解答】解:过D作DF⊥AE于F,延长DF交AC于D′,过D′作D′P′⊥AD于P′,D′P′交AE于Q′.
∵DD′⊥AE于F,
∴∠AFD=∠AFD′=90°,
∵∠DAC的平分线交DC于点E,
∴∠DAE=∠CAE,
∵在△DAF与△D′AF中,
,
∴△DAF≌△D′AF(ASA),
∴D′是D关于AE的对称点,AD=AD′,
∴D′P′即为DQ+PQ的最小值.
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′=2,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=8,
∴AD′=2,AD=AD′=2,
∴正方形ABCD的边长为2,
故选:D.
二、填空题(共6小题,每小题3分,计18分)
9.(3分)分解因式:x3﹣6x2+9x= x(x﹣3)2 .
【解答】解:x3﹣6x2+9x
=x(x2﹣6x+9)
=x(x﹣3)2,
故答案为:x(x﹣3)2.
10.(3分)一个多边形的内角和比四边形内角和的2倍多180°,这个多边形的边数是 7 .
【解答】解:∵四边形内角和为360°,
∴这个多边形内角和为360°×2+180°=900°,
∵多边形内角和为(n﹣2)×180°,
∴(n﹣2)×180°=900°,
∴n=7,
∴这个多边形的边数为:7,
故答案为:7.
11.(3分)计算: .
【解答】解:原式
,
故答案为:.
12.(3分)如图,将△ABC绕点B顺时针旋转100°,得到△EBD,若点E恰好在AC的延长线上,则∠CED的度数为 80° .
【解答】解:由题意得,△ABC≌△EBD,∠ABE=100°,
∴∠A=∠BED,AB=BE,
∴∠A=∠BEC,
∴∠CED=∠BEC+∠BED=80°,
故答案为:80°.
13.(3分)如图, ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若△ABE的周长为15,则 ABCD的周长为 30 .
【解答】解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵△ABE的周长为15,
∴AB+BE+AE=15,
∵OE⊥BD,
∴OE是线段BD的垂直平分线,
∴BE=ED,
∴AB+BE+AE=AB+AD=15,
∴ ABCD的周长=2(AB+AD)=2×15=30,
故答案为:30.
14.(3分)如图,在平面直角坐标系中,直线y1=2x和y2=kx+b(k、b为常数,k≠0)相交于点P(m,1),则不等式2x>kx+b的解集是 x .
【解答】解:将点P(m,1)代入y=2x,
得2m=1,
解得m,
∴P(,1),
根据图象,不等2x>kx+b的解集为x,
故答案为:x.
三、解答题(共8小题,计58分。解答应写出过程)
15.(5分)解不等式组:.
【解答】解:解第一个不等式去括号得2x+5≤3x+6,解得x≥﹣1;
解第二个不等式去分母得3x﹣3<2x,解得x<3;
∴不等式组的解集是﹣1≤x<3.
16.(5分)解分式方程:1.
【解答】解:1,
方程两边乘(x﹣2)2得:x(x﹣2)﹣(x﹣2)2=4,
解得:x=4,
检验:当x=4时,(x﹣2)2≠0.
所以原方程的解为x=4.
17.(7分)已知:如图,在 ABCD中,对角线AC、BD相交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:四边形AECF是平行四边形.
【解答】证明:在平行四边形ABCD中,
∵AE,CF分别为△ABD与△BCD的高,
∴AE=CF,
∵AE⊥BD,CF⊥BD,∴AE∥CF,
∴四边形AECF是平行四边形.
18.(7分)先化简,再求值:设x=3y,求的值.
【解答】解:
,
∵x=3y,
∴原式.
19.(8分)如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=40°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
【解答】(1)解:∵∠BAC=40°,AD平分∠BAC,
∴∠EAD∠BAC=20°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣20°=70°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
在△AED和△ACD中,
,
∴△AED≌△ACD(AAS),
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,AD平分线段EC,
即直线AD是线段CE的垂直平分线.
20.(8分)正所谓“道路通达,百业兴旺”,某村决定对村里的部分道路进行整改,将工程交由甲、乙两个工程队来完成.已知甲工程队每天比乙工程队多修0.4km,如果甲工程队修6.4km所用的天数是乙工程队修9.6km所用天数的一半.
(1)求甲,乙两个工程队每天各修路多少km?
(2)现计划再修建长度为24km的道路,由甲、乙两个工程队来完成.若甲队每天所需费用为2.4万元,乙队每天所需费用为1.5万元,求在总费用不超过33.6万元的情况下,至少安排乙工程队施工多少天?
【解答】解:(1)设乙工程队每天修路x km,则甲工程队每天修路(x+0.4)km,
根据题意得:,
解得:x=1.2,
经检验,x=1.2是所列方程的解,且符合题意,
∴x+0.4=1.2+0.4=1.6.
答:甲工程队每天修路1.6km,乙工程队每天修路1.2km;
(2)设安排乙工程队施工m天,则安排甲工程队施工天,
根据题意得:2.41.5m≤33.6,
解得:m≥8,
∴m的最小值为8.
答:至少安排乙工程队施工8天.
21.(8分)如图,已知直线y1=kx+b经过点A(﹣6,0),B(﹣1,5),直线y2=﹣2x+a与直线AB相交于点M,与x轴交于点D,点M的横坐标为﹣3.
(1)根据图象,直接写出当kx+b<﹣2x+a时,x的取值范围是什么?
(2)求直线AB的表达式和a的值;
(3)若点P在直线AB上,且S△ADP=9,求点P的坐标.
【解答】解:(1)由图象可知,当kx+b<﹣2x+a时,
x的取值范围为x<﹣3;
(2)由条件可得,
解得,
∴直线AB的表达式为y1=x+6,
把x=﹣3代入y1=x+6,
得y=3,
∴点M的坐标为(﹣3,3),
把(﹣3,3)代入y2=﹣2x+a,
得a=﹣3.
(3)设P(m,m+6),
把y=0代入y2=﹣2x﹣3得,x,
∴D(,0),
∵A(﹣6,0),
∴AD,
∴S△ADPAD |yP|=9,
∴|m+6|=9,
解得m=﹣2或﹣10.
∴P(﹣2,4)或(﹣10,﹣4).
22.(10分)探究,如图1所示,平行四边形ABCD中,AC与BD交于点O,过点O的直线分别交AD,BC于点E,F.
(1)求证:OE=OF;
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将平行四边形ABCD的面积分成二等份?试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图2所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请帮助张大爷把地分开.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,
∴∠EDO=∠FBO,
在△EDO和△FBO中,
,
∴△EDO≌△FBO(ASA),
∴OE=OF;
(2)由(1)知:△EDO≌△FBO,
∴DE=BF,
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△EAO和△FCO中,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴AE+BF=CF+DE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AE+BF+AB+EF=CF+DE+CD+EF,
即四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是将平行四边形ABCD的面积分成二等份,理由如下:
∵四边形ABCD是平行四边形,
∴OD=OB,OC=OA,
在△DOC和△BOA中,
,
∴△DOC≌△BOA(SAS),
∴S△DOC=S△BOA,
∵△EDO≌△FBO,△AOE≌△COF,
∴S△EDO=S△FBO,S△AOE=S△COF,
∴S△DOC+S△EDO+S△COF=S△BOA+S△FBO+S△AOE,
即四边形AEFB与四边形DEFC的面积相等,
∴直线EF是将平行四边形ABCD的面积分成二等份,
应用:连接AC、BD交于O,作直线OP交CD、AB于E、F,如图:
由(2)(3)可知,四边形AFED和四边形BFEC的周长和面积均相等,
∴把平行四边形的菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,则图中EF把平行四边形分成的两部分,符合题意.
同课章节目录
