四川省遂宁市2024-2025学年高一下学期7月期末教学水平监测数学试卷(含答案)
文档属性
| 名称 | 四川省遂宁市2024-2025学年高一下学期7月期末教学水平监测数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 521.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 00:00:00 | ||
图片预览



文档简介
遂宁市高中2027届第二学期期末教学水平监测
数 学 试 题
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。总分150分。考试时间120分钟。
第Ⅰ卷(选择题,满分58分)
注意事项:
1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。并检查条形码粘贴是否正确。
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知为虚数单位,复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.某校高一年级有男生160人,女生120人,现需抽调人参与学校“5.4”文艺汇演志愿者工作。若按性别分层,采用比例分配的分层随机抽样。已知男生抽取16人,则
A.27 B.28 C.29 D.30
3.已知两条直线若平面,,则与平面的位置关系是
A. 平面 B.⊥平面或 平面
C.∥平面 D.∥平面或 平面
4.已知两点,点在轴上,若三点共线,则点的坐标为
A. B. C. D.
5.圆锥的轴截面是等腰直角三角形,侧面积是,则圆锥的体积是
A. B. C.64π D.
6.若
A. B. C. D.
7.,则的最大值是
A. B. C. D.
8.函数,则在内零点个数为
A.5 B.6 C.7 D.8
二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.)
9.已知复数(是虚数单位),则下列结论正确的是
A.复数的虚部为 B.
C. D.若是实数,是纯虚数,则
10.如图所示,在四面体中,,,平面平面,则下列结论错误的是
A. B.
C.与平面所成的角为 D.四面体的体积为
11.在中,角的对边分别为,的面积为,且,下列选项正确的是
A.
B.的最大值为
C.若有两解,则取值范围是
D.若 ,O为的外心,则
第Ⅱ卷(非选择题,满分92分)
注意事项:
1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
2.试卷中横线及框内注有“▲”的地方,是需要你在第Ⅱ卷答题卡上作答。
三、填空题(本题共3小题,每小题5分,共15分.)
12.值是 ▲ .
函数,的部分
图象如图所示,则 ▲ .
世界上最不可思议的四面体就是勒洛四面体,它是以正四面
体的四个顶点为球心,以正四面体的棱长为半径的四个球的
相交部分围成的几何体。如图所示,若正四面体的棱
长为,则勒洛四面体能够容纳的最大球的半径为 ▲ .
四、解答题(本题共5小题,共77分,解答应写出文字说明 证明过程或演算步骤。)
15.(13分)在平面直角坐标系中,点为坐标原点,已知点,点,点
(1)求夹角的余弦值
(2)当是以角为直角的三角形时,求的值
▲
16.(15分)已知函数
求函数的单调递增区间
将函数的图象横坐标伸长为原来的2倍,纵坐标不变,再将所得图象向左平移
个单位长度后得到函数的图象。当时,求函数的值域
▲
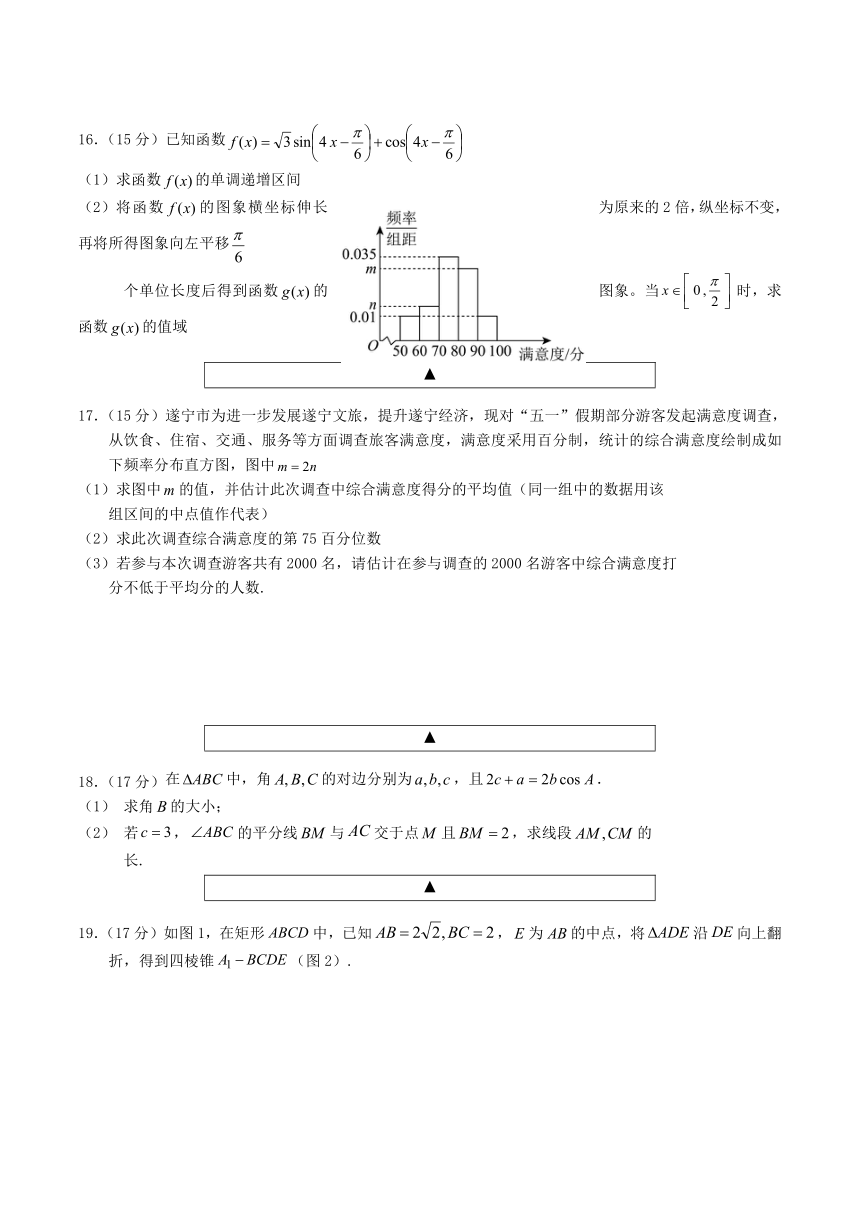
17.(15分)遂宁市为进一步发展遂宁文旅,提升遂宁经济,现对“五一”假期部分游客发起满意度调查,从饮食、住宿、交通、服务等方面调查旅客满意度,满意度采用百分制,统计的综合满意度绘制成如下频率分布直方图,图中
求图中的值,并估计此次调查中综合满意度得分的平均值(同一组中的数据用该
组区间的中点值作代表)
求此次调查综合满意度的第75百分位数
若参与本次调查游客共有2000名,请估计在参与调查的2000名游客中综合满意度打
分不低于平均分的人数.
▲
18.(17分)在中,角的对边分别为,且.
(1) 求角的大小;
(2) 若,的平分线与交于点且,求线段的
长.
▲
19.(17分)如图1,在矩形中,已知,为的中点,将沿向上翻折,得到四棱锥(图2).
(1)若为的中点,求证:;
(2)求证:;
(3)在翻折过程中,当二面角为时;在平面内有一动点满足:直线与底面所成角正弦值为,求动点的轨迹长度.
▲
遂宁市高中2027届第二学期教学水平监测
数学试题参考答案及评分意见
一、单选题(每个5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 A B D D A B C B
二、多选题(每个6分,共18分。全部选对的得6分,部分选对的得部分分,有选错的得0分.)
题号 9 10 11
答案 CD ABD ACD
三 填空题:(每小题5分,共15分.)
12. 13. 1 14.
四、解答题(本题共5小题,共77分,其中第15题13分,第16、17题15分,
第18、19题17分)
15.解:(1), ...................................................................( 2分)
, ...................................................................( 4分)
所以 ...................................................................( 6分)
(2)
因为是以角C为直角的三角形,所以...........................( 9分)
即
,..........................( 12分)
综上所述:.........................................................( 13分)
16.解: (1)
..................( 2分)
................( 4分)
令 ,则
函数的单调递增区间为..........................( 7分)
(2)函数的图象横坐标伸长为原来的倍,纵坐标不变,得...( 9分)
再将图象向左平移个单位长度得 ......( 11分)
, ...............( 14分)
综上所述:函数的值域为 ..............................( 15分)
17、解 (1)由频率分布直方图可得,,
又解得 . ............ ( 2分)
平均分为 (5分)
(2)由频率分布直方图可得,前3组频率之和为0.6,第四组频率为0.3 ..... ( 6分)
故第75百分位数在 则. .( 10分)
由(1)知平均分为
故不低于平均分的频率为 ............( 14分)
打分不低于平均分的人数为 ...( 15分)
18.解:(1) 由正弦定理
可得....................................(2分)
所以
所以.............................................................(5分)
因为,所以 ,即..............(7分)
因为 所以.........................................(8分)
(2)在中,由面积分割可得:
即
所以.............................................................(11分)
由余弦定理
所以,...............................................(13分)
即 ①
由角平分线的性质有 ②...................................................(15分)
由①②可得,.............................................................(17分)
19.证明:(1)取的中点,连接,因为分别为的中点,,.........................1分
因为四边形为矩形,所以,
又因为为的中点,所以;所以
所以四边形为平行四边形。..........................3分
;
.........................4分
(2)
在图(1)中,连接,所以
又因为;同理:
........................6分;
由翻折性质得:
.........................9分
(3)解:过作垂足为;
由(2)知:,
所以;
过作垂足为,连接
.
.........................12分
由题意,知:
在
.......................15分
,
,且
所以动点的轨迹为以为圆心,为半径的圆;
所以动点R的轨迹长度为....................17分
数 学 试 题
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。总分150分。考试时间120分钟。
第Ⅰ卷(选择题,满分58分)
注意事项:
1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。并检查条形码粘贴是否正确。
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知为虚数单位,复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.某校高一年级有男生160人,女生120人,现需抽调人参与学校“5.4”文艺汇演志愿者工作。若按性别分层,采用比例分配的分层随机抽样。已知男生抽取16人,则
A.27 B.28 C.29 D.30
3.已知两条直线若平面,,则与平面的位置关系是
A. 平面 B.⊥平面或 平面
C.∥平面 D.∥平面或 平面
4.已知两点,点在轴上,若三点共线,则点的坐标为
A. B. C. D.
5.圆锥的轴截面是等腰直角三角形,侧面积是,则圆锥的体积是
A. B. C.64π D.
6.若
A. B. C. D.
7.,则的最大值是
A. B. C. D.
8.函数,则在内零点个数为
A.5 B.6 C.7 D.8
二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.)
9.已知复数(是虚数单位),则下列结论正确的是
A.复数的虚部为 B.
C. D.若是实数,是纯虚数,则
10.如图所示,在四面体中,,,平面平面,则下列结论错误的是
A. B.
C.与平面所成的角为 D.四面体的体积为
11.在中,角的对边分别为,的面积为,且,下列选项正确的是
A.
B.的最大值为
C.若有两解,则取值范围是
D.若 ,O为的外心,则
第Ⅱ卷(非选择题,满分92分)
注意事项:
1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
2.试卷中横线及框内注有“▲”的地方,是需要你在第Ⅱ卷答题卡上作答。
三、填空题(本题共3小题,每小题5分,共15分.)
12.值是 ▲ .
函数,的部分
图象如图所示,则 ▲ .
世界上最不可思议的四面体就是勒洛四面体,它是以正四面
体的四个顶点为球心,以正四面体的棱长为半径的四个球的
相交部分围成的几何体。如图所示,若正四面体的棱
长为,则勒洛四面体能够容纳的最大球的半径为 ▲ .
四、解答题(本题共5小题,共77分,解答应写出文字说明 证明过程或演算步骤。)
15.(13分)在平面直角坐标系中,点为坐标原点,已知点,点,点
(1)求夹角的余弦值
(2)当是以角为直角的三角形时,求的值
▲
16.(15分)已知函数
求函数的单调递增区间
将函数的图象横坐标伸长为原来的2倍,纵坐标不变,再将所得图象向左平移
个单位长度后得到函数的图象。当时,求函数的值域
▲
17.(15分)遂宁市为进一步发展遂宁文旅,提升遂宁经济,现对“五一”假期部分游客发起满意度调查,从饮食、住宿、交通、服务等方面调查旅客满意度,满意度采用百分制,统计的综合满意度绘制成如下频率分布直方图,图中
求图中的值,并估计此次调查中综合满意度得分的平均值(同一组中的数据用该
组区间的中点值作代表)
求此次调查综合满意度的第75百分位数
若参与本次调查游客共有2000名,请估计在参与调查的2000名游客中综合满意度打
分不低于平均分的人数.
▲
18.(17分)在中,角的对边分别为,且.
(1) 求角的大小;
(2) 若,的平分线与交于点且,求线段的
长.
▲
19.(17分)如图1,在矩形中,已知,为的中点,将沿向上翻折,得到四棱锥(图2).
(1)若为的中点,求证:;
(2)求证:;
(3)在翻折过程中,当二面角为时;在平面内有一动点满足:直线与底面所成角正弦值为,求动点的轨迹长度.
▲
遂宁市高中2027届第二学期教学水平监测
数学试题参考答案及评分意见
一、单选题(每个5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 A B D D A B C B
二、多选题(每个6分,共18分。全部选对的得6分,部分选对的得部分分,有选错的得0分.)
题号 9 10 11
答案 CD ABD ACD
三 填空题:(每小题5分,共15分.)
12. 13. 1 14.
四、解答题(本题共5小题,共77分,其中第15题13分,第16、17题15分,
第18、19题17分)
15.解:(1), ...................................................................( 2分)
, ...................................................................( 4分)
所以 ...................................................................( 6分)
(2)
因为是以角C为直角的三角形,所以...........................( 9分)
即
,..........................( 12分)
综上所述:.........................................................( 13分)
16.解: (1)
..................( 2分)
................( 4分)
令 ,则
函数的单调递增区间为..........................( 7分)
(2)函数的图象横坐标伸长为原来的倍,纵坐标不变,得...( 9分)
再将图象向左平移个单位长度得 ......( 11分)
, ...............( 14分)
综上所述:函数的值域为 ..............................( 15分)
17、解 (1)由频率分布直方图可得,,
又解得 . ............ ( 2分)
平均分为 (5分)
(2)由频率分布直方图可得,前3组频率之和为0.6,第四组频率为0.3 ..... ( 6分)
故第75百分位数在 则. .( 10分)
由(1)知平均分为
故不低于平均分的频率为 ............( 14分)
打分不低于平均分的人数为 ...( 15分)
18.解:(1) 由正弦定理
可得....................................(2分)
所以
所以.............................................................(5分)
因为,所以 ,即..............(7分)
因为 所以.........................................(8分)
(2)在中,由面积分割可得:
即
所以.............................................................(11分)
由余弦定理
所以,...............................................(13分)
即 ①
由角平分线的性质有 ②...................................................(15分)
由①②可得,.............................................................(17分)
19.证明:(1)取的中点,连接,因为分别为的中点,,.........................1分
因为四边形为矩形,所以,
又因为为的中点,所以;所以
所以四边形为平行四边形。..........................3分
;
.........................4分
(2)
在图(1)中,连接,所以
又因为;同理:
........................6分;
由翻折性质得:
.........................9分
(3)解:过作垂足为;
由(2)知:,
所以;
过作垂足为,连接
.
.........................12分
由题意,知:
在
.......................15分
,
,且
所以动点的轨迹为以为圆心,为半径的圆;
所以动点R的轨迹长度为....................17分
同课章节目录
