山东省淄博市2024-2025学年高二下学期期末教学质量检测数学试卷(图片版,含答案)
文档属性
| 名称 | 山东省淄博市2024-2025学年高二下学期期末教学质量检测数学试卷(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 17:18:27 | ||
图片预览




文档简介
参照秘密级管理★启用前
2024一2025学年度第二学期高二教学质量检测
数学
注意事项:
1、答卷前,考生务必将自已的姓名、考生号等填写在答题卡和试卷指定位置上,
2.回答选择题时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写
在答题卡上,写在本试卷上无效,
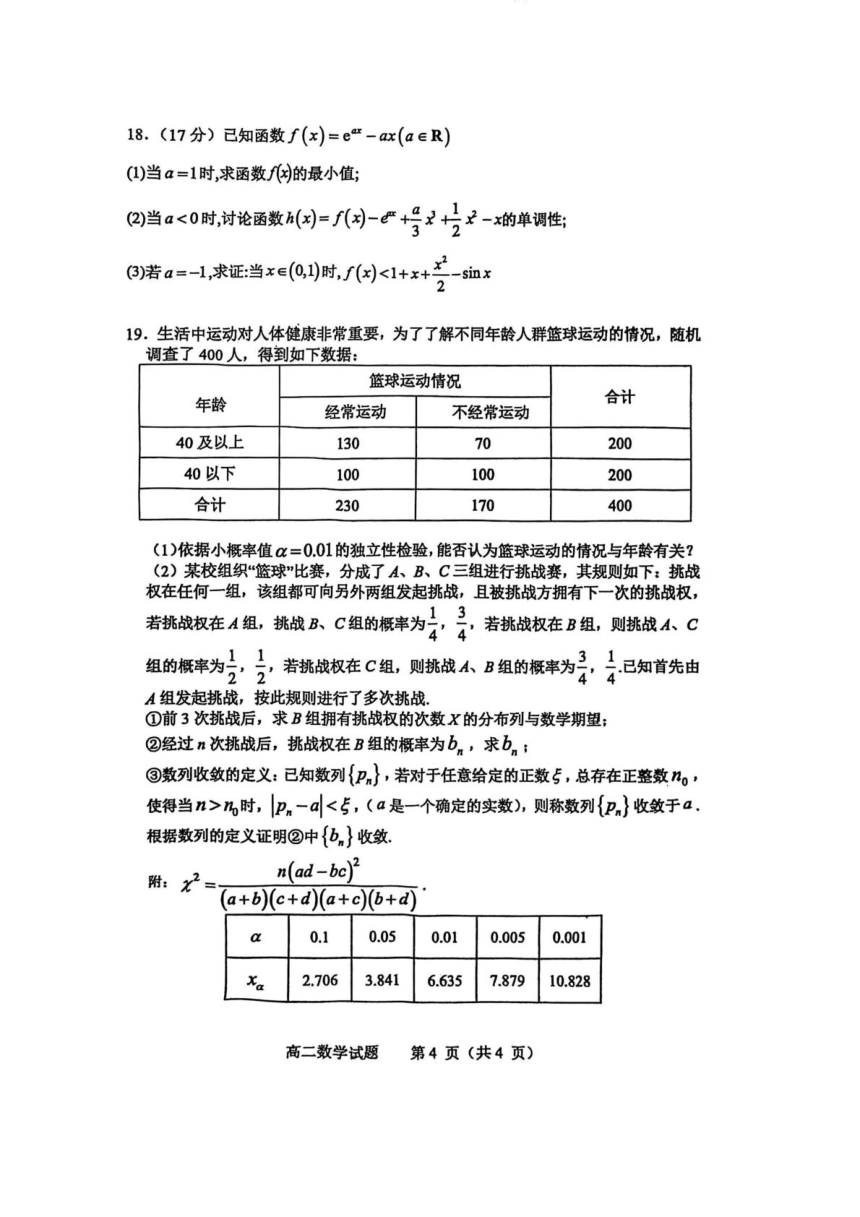
3.考试结束后,将本试卷和答题卡一并交回.
单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项
中,只有一项是符合题目要求的,
1.已知数列{an}是等差数列,42=-2,44=4,则40=()
A.22
B.24
C.16
D.18
2.已知随机变量X服从正态分布N(3,7),P(X>2)=0.8,则P(X≥4)=()
吹
A.0.7
B.0.3
C.0.8
D.0.2
3.已知数列{an}是等比数列,a2,a是方程x2-40x+25=0的两个根,则4,=()
A.5
B.-5
C.5或5
D
4.有三台车床加工同一型号的零件,第1台加工的次品率为%,第2,3台加工的次
品率均为8%,加工出来的零件混放在一起,已知第1,2,3台车床加工的零件数
分别占总数的25%,30%,45%,任取一个零件,则它是次品的概率()
A.0.078
B.0.077
C.0.076
D.0.075
5.若函数f问)2-x+是增函数,则的取值范围是《)
2
A.(-o,1)
B,(-o,1]
C.(-9,2]
D.(-∞,2)
6.从装有3个白球、4个红球的箱子中无放回地随机取两次,每次取一个球,A表示
事件“两次取出的球颜色相同”,B表示事件“两次取出的球中至少有1个是红球”,
则P(BA)=()
B.
8
C.
6-7
7.数列(a,}满足4=-1,且出=+2
nG+D(EN).
则42025=()
A.2022
B.2023
C.2024
D.2025
高二数学试题
第1页(共4页)
8.已知f(x)为定义在R上的可导函数,f(x)为其导函数,且f(x)其中e是自然对数的底,则()
A.f(2024)B.ef(2024)C.ef(2024)=f(2025)
D.ef(2024>f(2025
二.多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项
中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0
分.
9.以下结论正确的是()
A.在线性回归分析中,样本相关系数”的值越大,变量间的线性相关性越强
B.经验回归直线)=x+a一定经过点(民,)
C.一组数据(1,3),(2,8),(3,10),(4,14),(5,15)的经验回归方程为=3x+à,则当x=2
时,残差为1
D.以模型y=“(k>0)去拟合一组数据时,为了利用一元线性回归模型估计参
数k,c,设z=my,将其变换后得到线性方程z=0.4x+3,则k,c的值分别是e3和
0.4
10.已知函数f(x)=(3x-10)=a+4(x-2)+a2(x-2)}2+…+40(x-2)°,则()
A.a+4+a2+…+a0=710
B.a+a+a+…t46=7+l
2
C.42=-40×39
D.f(13)的个位数字是9
11.牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法一牛顿法.具
体步骤如下:设r是函数y=f(x)的一个零点,任意选取x作为r的初始近似值,
在横坐标为x的点处作曲线∫(x)的切线,直线马与x轴交点的横坐标为,;用
代替x重复上面过程得到x;一直进行下去,得到x,,,x,当xn一x-足够
小时,我们可以把xn的值作为函数f(x)零点的近似值.已知函数f(x)=x+3x-2,
=1,则下列说法正确的是()
A.切线l的方程为6x-y-4=0
高二数学试题
第2页(共4页)
2024一2025学年度第二学期高二教学质量检测
数学
注意事项:
1、答卷前,考生务必将自已的姓名、考生号等填写在答题卡和试卷指定位置上,
2.回答选择题时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写
在答题卡上,写在本试卷上无效,
3.考试结束后,将本试卷和答题卡一并交回.
单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项
中,只有一项是符合题目要求的,
1.已知数列{an}是等差数列,42=-2,44=4,则40=()
A.22
B.24
C.16
D.18
2.已知随机变量X服从正态分布N(3,7),P(X>2)=0.8,则P(X≥4)=()
吹
A.0.7
B.0.3
C.0.8
D.0.2
3.已知数列{an}是等比数列,a2,a是方程x2-40x+25=0的两个根,则4,=()
A.5
B.-5
C.5或5
D
4.有三台车床加工同一型号的零件,第1台加工的次品率为%,第2,3台加工的次
品率均为8%,加工出来的零件混放在一起,已知第1,2,3台车床加工的零件数
分别占总数的25%,30%,45%,任取一个零件,则它是次品的概率()
A.0.078
B.0.077
C.0.076
D.0.075
5.若函数f问)2-x+是增函数,则的取值范围是《)
2
A.(-o,1)
B,(-o,1]
C.(-9,2]
D.(-∞,2)
6.从装有3个白球、4个红球的箱子中无放回地随机取两次,每次取一个球,A表示
事件“两次取出的球颜色相同”,B表示事件“两次取出的球中至少有1个是红球”,
则P(BA)=()
B.
8
C.
6-7
7.数列(a,}满足4=-1,且出=+2
nG+D(EN).
则42025=()
A.2022
B.2023
C.2024
D.2025
高二数学试题
第1页(共4页)
8.已知f(x)为定义在R上的可导函数,f(x)为其导函数,且f(x)
A.f(2024)
D.ef(2024>f(2025
二.多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项
中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0
分.
9.以下结论正确的是()
A.在线性回归分析中,样本相关系数”的值越大,变量间的线性相关性越强
B.经验回归直线)=x+a一定经过点(民,)
C.一组数据(1,3),(2,8),(3,10),(4,14),(5,15)的经验回归方程为=3x+à,则当x=2
时,残差为1
D.以模型y=“(k>0)去拟合一组数据时,为了利用一元线性回归模型估计参
数k,c,设z=my,将其变换后得到线性方程z=0.4x+3,则k,c的值分别是e3和
0.4
10.已知函数f(x)=(3x-10)=a+4(x-2)+a2(x-2)}2+…+40(x-2)°,则()
A.a+4+a2+…+a0=710
B.a+a+a+…t46=7+l
2
C.42=-40×39
D.f(13)的个位数字是9
11.牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法一牛顿法.具
体步骤如下:设r是函数y=f(x)的一个零点,任意选取x作为r的初始近似值,
在横坐标为x的点处作曲线∫(x)的切线,直线马与x轴交点的横坐标为,;用
代替x重复上面过程得到x;一直进行下去,得到x,,,x,当xn一x-足够
小时,我们可以把xn的值作为函数f(x)零点的近似值.已知函数f(x)=x+3x-2,
=1,则下列说法正确的是()
A.切线l的方程为6x-y-4=0
高二数学试题
第2页(共4页)
同课章节目录
