2024-2025学年四川省绵阳市涪城区七年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年四川省绵阳市涪城区七年级(下)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 21:31:24 | ||
图片预览




文档简介
2024-2025学年四川省绵阳市涪城区七年级(下)期末数学试卷
一.选择题(每小题3分,共36分)
1.(3分)的相反数是( )
A.5 B.0 C. D.
2.(3分)下列调查中,适合用普查方式的是( )
A.检测某城市空气质量
B.检测神舟十三号载人飞船的零部件质量情况
C.检测一批节能灯的使用寿命
D.检测某批次汽车的抗撞能力
3.(3分)已知a,b,c,d是实数,且a﹣b>c﹣d,下列说法一定正确的是( )
A.若b=d,则a>c B.若a=c,则b>d
C.若b<d,则a>c D.若a>c,则b>d
4.(3分)关于x的不等式(a﹣3)x>a﹣3的解集是x>1,则a的取值范围是( )
A.a>3 B.a<3 C.a>1 D.a<1
5.(3分)如图,小手盖住的点的坐标可能为( )
A.(﹣1,﹣2) B.(﹣2,3) C.(2,0) D.(2,﹣3)
6.(3分)下列命题是假命题的是( )
A.“对顶角相等”的逆命题是假命题
B.在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c
C.两条平行线被第三条直线所截,内错角相等
D.同旁内角互补两直线平行
7.(3分)下列各式中,正确的是( )
A.4 B.± C.±± D.±4
8.(3分)把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
A.26° B.24° C.22° D.20°
9.(3分)圆圆读一本故事书,第一天读了全书的,第二天读了剩下的,这时还有36页没读,则她第二天读的页数为( )
A.18 B.16 C.36 D.12
10.(3分)课后延时服务已经落地,为了进一步对课后延时服务进行规范,某校计划在延时服务时间内开展各种社团活动.小明对全校学生进行抽样调查,收集整理拟参加社团活动类型(A.读书交流,B.体育锻炼,C.戏剧说唱,D.手工陶艺)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400
B.类型D所对应的扇形的圆心角为36
C.类型C所占的百分比为30%
D.类型B的人数为120人
11.(3分)某电梯乘载的质量超过300千克时会响起警示音,已知小华、小欧的体重分别为45千克、70千克.小华进入电梯,警示音没响,小欧在小华之后进入电梯,警示音响起.设电梯在两人进入前已乘载的质量为x千克,则x满足( )
A.185<x≤255 B.185≤x<255 C.230<x≤255 D.230≤x<255
12.(3分)如图,线段AB∥CD,AE∥CF,∠D﹣∠C=α,EP⊥AB于点P,EM平分∠AEB交AB于点M,则∠PEM的度数是( )
A. B. C.α D.2α
二.填空题(每小题3分,共18分)
13.(3分)如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC的度数是138°,第二次的拐角∠BCD的度数是 .
14.(3分)点(﹣5,3)到x轴上的距离是 .
15.(3分)某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛.在最近的10次选拔赛中,他们的成绩(单位:cm)折线统计图如图所示:
历届比赛成绩表明,成绩达到5.96m就很可能夺冠.若为了稳妥夺冠,则应选择参赛的运动员是 (填“甲”或“乙”).
16.(3分)已知关于x、y的二元一次方程组的解满足x﹣y>2,则m的最大整数值为m= .
17.(3分)如图,在由小正方形组成的网格图中,有a,b两户家用电路接入电表,a户电路接点与电表接入点之间所用电线长度为5m,则b户电路接点与电表接入点之间所用电线长度为 m.
18.(3分)若关于x的不等式组恰有3个整数解,则m的取值范围是 .
三.解答题(共46分)
19.计算:﹣12025﹣|1|+2cos30°+()﹣2.
20.解方程组:.
21.在平面直角坐标系中,△ABC经过平移得到三角形△A′B′C′,位置如图所示:
(1)分别写出点A、A'的坐标:A ,A' ;
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求△ABC的面积.
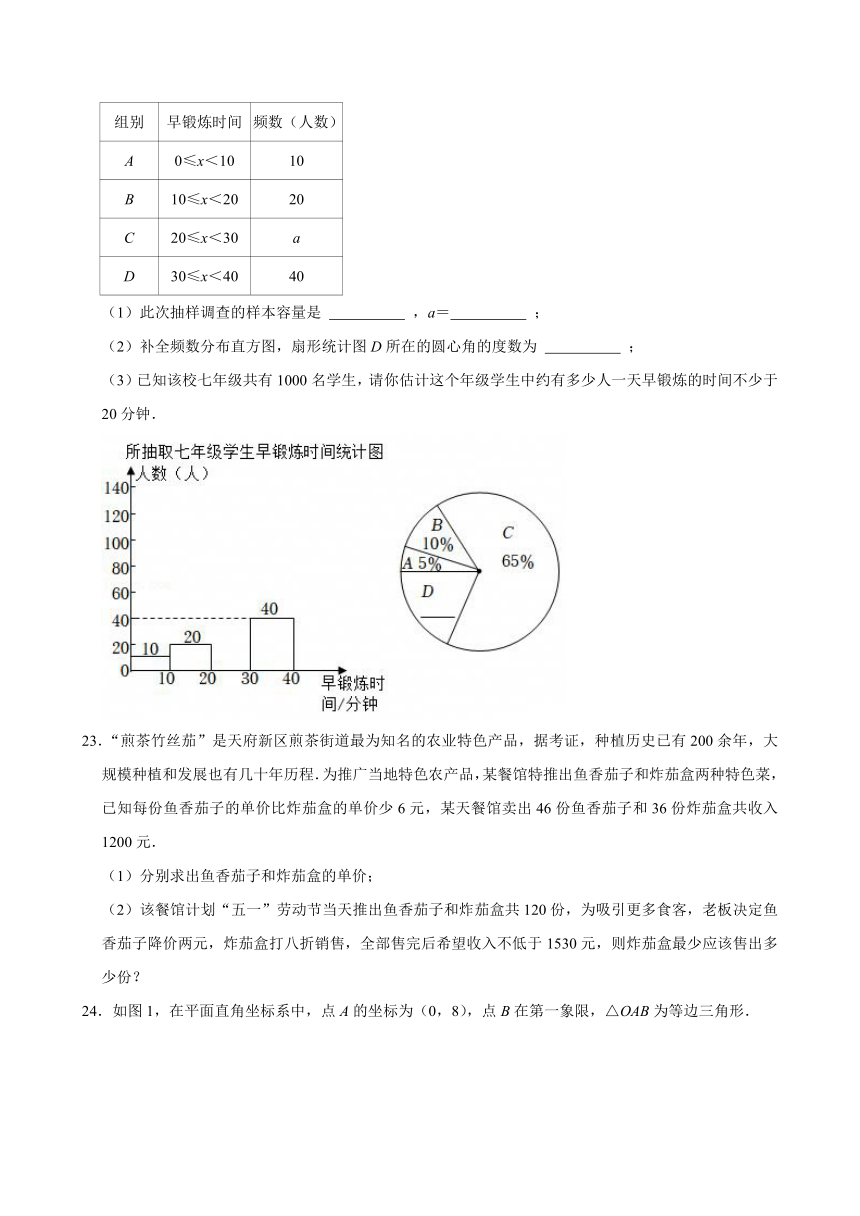
22.养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,教务处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A,B,C,D四组,如表所示.同时将调查结果绘制成下面两幅不完整的统计图.
请根据以上的信息,解答下列问题:
组别 早锻炼时间 频数(人数)
A 0≤x<10 10
B 10≤x<20 20
C 20≤x<30 a
D 30≤x<40 40
(1)此次抽样调查的样本容量是 ,a= ;
(2)补全频数分布直方图,扇形统计图D所在的圆心角的度数为 ;
(3)已知该校七年级共有1000名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.
23.“煎茶竹丝茄”是天府新区煎茶街道最为知名的农业特色产品,据考证,种植历史已有200余年,大规模种植和发展也有几十年历程.为推广当地特色农产品,某餐馆特推出鱼香茄子和炸茄盒两种特色菜,已知每份鱼香茄子的单价比炸茄盒的单价少6元,某天餐馆卖出46份鱼香茄子和36份炸茄盒共收入1200元.
(1)分别求出鱼香茄子和炸茄盒的单价;
(2)该餐馆计划“五一”劳动节当天推出鱼香茄子和炸茄盒共120份,为吸引更多食客,老板决定鱼香茄子降价两元,炸茄盒打八折销售,全部售完后希望收入不低于1530元,则炸茄盒最少应该售出多少份?
24.如图1,在平面直角坐标系中,点A的坐标为(0,8),点B在第一象限,△OAB为等边三角形.
(1)直接写出点B的纵坐标 ;
(2)如图2,OC⊥AB于点C,点C关于x轴的对称点为点D,则点D的纵坐标为 ;
(3)OC⊥AB于点C,点C关于x轴的对称点为点D,连接AD交OB于E,求OE的长.
2024-2025学年四川省绵阳市涪城区七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共12小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D B A A D B C B A C A
题号 12
答案 A
一.选择题(每小题3分,共36分)
1.(3分)的相反数是( )
A.5 B.0 C. D.
【解答】解:的相反数是:.
故选:D.
2.(3分)下列调查中,适合用普查方式的是( )
A.检测某城市空气质量
B.检测神舟十三号载人飞船的零部件质量情况
C.检测一批节能灯的使用寿命
D.检测某批次汽车的抗撞能力
【解答】解:A.检测某城市空气质量,适合抽样调查,故不符合题意;
B.检测神舟十三号载人飞船的零部件质量情况,适合普查,故符合题意;
C.检测一批节能灯的使用寿命,适合抽样调查,故不符合题意;
D.检测某批次汽车的抗撞能力,适合抽样调查,不符合题意.
故选:B.
3.(3分)已知a,b,c,d是实数,且a﹣b>c﹣d,下列说法一定正确的是( )
A.若b=d,则a>c B.若a=c,则b>d
C.若b<d,则a>c D.若a>c,则b>d
【解答】解:A、若b=d,a﹣b>c﹣d,则a>c,故此选项符合题意;
B、若a=c,a﹣b>c﹣d,则b<d,故此选项不符合题意;
C、若b<d,a﹣b>c﹣d,则a>c不一定成立,如a=1,c=3,b=2,d=5,故此选项不符合题意;
D、若a>c,a﹣b>c﹣d,则b>d不一定成立,有可能b=d,故此选项不符合题意;
故选:A.
4.(3分)关于x的不等式(a﹣3)x>a﹣3的解集是x>1,则a的取值范围是( )
A.a>3 B.a<3 C.a>1 D.a<1
【解答】解:∵关于x的不等式(a﹣3)x>a﹣3的解集是x>1,
∴a﹣3>0,
解得a>3.
故选:A.
5.(3分)如图,小手盖住的点的坐标可能为( )
A.(﹣1,﹣2) B.(﹣2,3) C.(2,0) D.(2,﹣3)
【解答】解:A.(﹣1,﹣2)在第三象限,故本选项不符合题意;
B.(﹣2,3)在第二象限,故本选项不符合题意;
C.(2,0)在x轴上,故本选项不符合题意;
D.(2,﹣3)在第四象限,故本选项符合题意.
故选:D.
6.(3分)下列命题是假命题的是( )
A.“对顶角相等”的逆命题是假命题
B.在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c
C.两条平行线被第三条直线所截,内错角相等
D.同旁内角互补两直线平行
【解答】解:“对顶角相等”的逆命题是“相等的角是对顶角“,逆命题为假命题,故A为真命题,不符合题意;
在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a⊥c,故B是假命题,符合题意;
两条平行线被第三条直线所截,内错角相等,故C是真命题,不符合题意;
同旁内角互补,两直线平行,故D是真命题,不符合题意;
故选:B.
7.(3分)下列各式中,正确的是( )
A.4 B.± C.±± D.±4
【解答】解:A、,本选项错误,
B、,本选项错误,
C、±±,本选项正确,
D、4,本选项错误,
故选:C.
8.(3分)把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
A.26° B.24° C.22° D.20°
【解答】解:如图,
∵直角三角板位于两条平行线间且∠1=54°,
∴∠3=126°,
又∵直角三角板含30°角,
∴180°﹣∠2﹣∠3=30°,
∴∠2=24°,
故选:B.
9.(3分)圆圆读一本故事书,第一天读了全书的,第二天读了剩下的,这时还有36页没读,则她第二天读的页数为( )
A.18 B.16 C.36 D.12
【解答】解:设这本故事书有x页,由题意得:
xx(xx)=36,
∴xxx=36,
∴x=36,
∴x=81,
∴(xx)(8181)=18.
故选:A.
10.(3分)课后延时服务已经落地,为了进一步对课后延时服务进行规范,某校计划在延时服务时间内开展各种社团活动.小明对全校学生进行抽样调查,收集整理拟参加社团活动类型(A.读书交流,B.体育锻炼,C.戏剧说唱,D.手工陶艺)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400
B.类型D所对应的扇形的圆心角为36
C.类型C所占的百分比为30%
D.类型B的人数为120人
【解答】解:样本容量为:100÷25%=400人,故选项A不合题意;
类型D所对应的扇形的圆心角为360°×10%=36°,故选项B不合题意;
类型C所占的百分比为:,故选项C符合题意;
类型B的人数为:400×(1﹣25%﹣10%﹣35%)=120(人),故选项D不合题意.
故选:C.
11.(3分)某电梯乘载的质量超过300千克时会响起警示音,已知小华、小欧的体重分别为45千克、70千克.小华进入电梯,警示音没响,小欧在小华之后进入电梯,警示音响起.设电梯在两人进入前已乘载的质量为x千克,则x满足( )
A.185<x≤255 B.185≤x<255 C.230<x≤255 D.230≤x<255
【解答】解:由题意得:,
解得:185<x≤255,
故选:A.
12.(3分)如图,线段AB∥CD,AE∥CF,∠D﹣∠C=α,EP⊥AB于点P,EM平分∠AEB交AB于点M,则∠PEM的度数是( )
A. B. C.α D.2α
【解答】解:∵AB∥CD,AE∥CF,
∴∠AEF=∠CFE,∠B=∠D(两直线平行,内错角相等),
∵∠CFE=∠D+∠C,∠D﹣∠C=α,
∴∠AEF=∠CFE=2∠C+α,∠D=∠B=∠C+α,
∴∠AEB=180°﹣2∠C﹣α,
∵EM平分∠AEB,
∴,
∵EP⊥AB,
∴∠EPB=90°,
∴∠PEB=90°﹣∠B=90°﹣∠C﹣α,
∴,
综上所述,只有选项A正确,符合题意,
故选:A.
二.填空题(每小题3分,共18分)
13.(3分)如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC的度数是138°,第二次的拐角∠BCD的度数是 138° .
【解答】解:AB∥CD,
∴∠BCD=∠ABC=138°.
故答案为:138°.
14.(3分)点(﹣5,3)到x轴上的距离是 3 .
【解答】解:点(﹣5,3)到x轴上的距离是|3|=3.
故答案为:3.
15.(3分)某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛.在最近的10次选拔赛中,他们的成绩(单位:cm)折线统计图如图所示:
历届比赛成绩表明,成绩达到5.96m就很可能夺冠.若为了稳妥夺冠,则应选择参赛的运动员是 甲 (填“甲”或“乙”).
【解答】解:∵甲成绩由小到大排列为:585,596,597,598,600,601,604,610,612,613,
∴甲成绩的中位数为:(600+601)÷2=600.5(cm),
甲成绩的平均数为:(585+596+597+598+600=601+604+610+612+613)÷10=601.6(分);
∵乙成绩由小到大排列为:574,580,585,590,593,598,613,618,618,624,
∴乙成绩的中位数为:(593+598)÷2=595.5(cm),
乙成绩的平均数为:(574+580+585+590+593+598+613+618+618+624)÷10=599.3(cm),
∵甲成绩的平均数高于乙平均数,甲成绩的中位数高于乙中位数,从折线统计图可以看出甲的成绩波动较小,且甲10次成绩中有9次达到夺冠的成绩,乙只有5次达到夺冠的成绩,
∴应选择参赛的运动员是:甲.
故答案为:甲.
16.(3分)已知关于x、y的二元一次方程组的解满足x﹣y>2,则m的最大整数值为m= ﹣2 .
【解答】解:,
由②﹣①得:x﹣y=1﹣m,
∵x﹣y>2,
∴1﹣m>2,
∴m<﹣1,
m的最大整数值为﹣2.
故答案为:﹣2.
17.(3分)如图,在由小正方形组成的网格图中,有a,b两户家用电路接入电表,a户电路接点与电表接入点之间所用电线长度为5m,则b户电路接点与电表接入点之间所用电线长度为 5 m.
【解答】解:由平移可知,
a,b两户的电线竖直方向和水平方向的长度相同,
所以b户电路接点与电表接入点之间的电线长度为5m.
故答案为:5.
18.(3分)若关于x的不等式组恰有3个整数解,则m的取值范围是 4<m≤5 .
【解答】解:.
解①得,x<m.
解②得,x≥2.
∴不等式组的解集为2≤x<m.
∵不等式组有3个整数解.
∴这3个整数解为:2,3,4.
∴m的取值范围为:4<m≤5.
故答案为:4<m≤5.
三.解答题(共46分)
19.计算:﹣12025﹣|1|+2cos30°+()﹣2.
【解答】解:原式=﹣1﹣(1)+24
=﹣114
=4.
20.解方程组:.
【解答】解:整理得,
①×2得,10x﹣4y=6③,
③﹣②得7x=7,
解得x=1,
将x=1代入①得5×1﹣2y=3,
解得y=1,
所以方程组的解为.
21.在平面直角坐标系中,△ABC经过平移得到三角形△A′B′C′,位置如图所示:
(1)分别写出点A、A'的坐标:A (1,0) ,A' (﹣4,4) ;
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为 (m﹣5,n+4) ;
(3)求△ABC的面积.
【解答】解:(1)由图知A(1,0),A'(﹣4,4);
(2)A(1,0)对应点的对应点A′(﹣4,4)得A向左平移5个单位,向上平移4个单位得到A′,
故△ABC内M(m,n)平移后对应点M'的坐标为(m﹣5,n+4);
(3)△ABC的面积为:4×44×23×21×4=7.
22.养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,教务处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A,B,C,D四组,如表所示.同时将调查结果绘制成下面两幅不完整的统计图.
请根据以上的信息,解答下列问题:
组别 早锻炼时间 频数(人数)
A 0≤x<10 10
B 10≤x<20 20
C 20≤x<30 a
D 30≤x<40 40
(1)此次抽样调查的样本容量是 200 ,a= 130 ;
(2)补全频数分布直方图,扇形统计图D所在的圆心角的度数为 72° ;
(3)已知该校七年级共有1000名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.
【解答】解:(1)10÷5%=200(人),a=200﹣10﹣20﹣40=130,
故答案为:200,130;
(2)补全频数分布直方图如下:
扇形D所对应的圆心角度数为:360°72°,
故答案为:72°;
(3)1000850(人),
答:该校七年级1000名学生中约有850人一天早锻炼的时间不少于20分钟.
23.“煎茶竹丝茄”是天府新区煎茶街道最为知名的农业特色产品,据考证,种植历史已有200余年,大规模种植和发展也有几十年历程.为推广当地特色农产品,某餐馆特推出鱼香茄子和炸茄盒两种特色菜,已知每份鱼香茄子的单价比炸茄盒的单价少6元,某天餐馆卖出46份鱼香茄子和36份炸茄盒共收入1200元.
(1)分别求出鱼香茄子和炸茄盒的单价;
(2)该餐馆计划“五一”劳动节当天推出鱼香茄子和炸茄盒共120份,为吸引更多食客,老板决定鱼香茄子降价两元,炸茄盒打八折销售,全部售完后希望收入不低于1530元,则炸茄盒最少应该售出多少份?
【解答】解:(1)设鱼香茄子的单价为x元,炸茄盒的单价为y元,
由题意得:,
解得:,
答:鱼香茄子的单价为12元,炸茄盒的单价为18元;
(2)设炸茄盒应该售出m份,则鱼香茄子应该售出(120﹣m)份,
由题意得:(12﹣2)(120﹣m)+18×0.8m≥1530,
解得:m≥75,
答:炸茄盒最少应该售出75份.
24.如图1,在平面直角坐标系中,点A的坐标为(0,8),点B在第一象限,△OAB为等边三角形.
(1)直接写出点B的纵坐标 (4,4) ;
(2)如图2,OC⊥AB于点C,点C关于x轴的对称点为点D,则点D的纵坐标为 ﹣6 ;
(3)OC⊥AB于点C,点C关于x轴的对称点为点D,连接AD交OB于E,求OE的长.
【解答】解:(1)如图1,过点B作BH⊥AO于H,
∵点A的坐标为(0,8),
∴OA=8,
∵△OAB为等边三角形,BH⊥AO,
∴AO=BO=AB=8,AH=OH=4,
∴BH4,
∴点B(4,4),
故答案为:(4,4);
(2)过点B作BH⊥AO于H,过点C作CG⊥AO于G,连接CH,连接CD交BO于N,
∵OC⊥AB,△OAB是等边三角形,
∴AC=BC,
∵BH⊥AO,
∴CH=AC=BC=4,
又∵CG⊥AH,
∴AG=GH=2,
∴OG=6,
∴点C的纵坐标为6,
∵点C关于x轴的对称点为点D,
∴点D的纵坐标﹣6;
故答案为:﹣6;
(3)∵CD⊥x轴,
∴CD=12,CD∥AO,
∴∠D=∠OAE,∠BCN=∠BAO=60°,∠BNC=∠AOB=60°,
∴△CNB是等边三角形,
∴CN=BC=4=BN=ON,
∴ND=8=AO,
又∵∠AEO=∠DEN,
∴△AEO≌△DEN(AAS),
∴OE=ENON=2.
一.选择题(每小题3分,共36分)
1.(3分)的相反数是( )
A.5 B.0 C. D.
2.(3分)下列调查中,适合用普查方式的是( )
A.检测某城市空气质量
B.检测神舟十三号载人飞船的零部件质量情况
C.检测一批节能灯的使用寿命
D.检测某批次汽车的抗撞能力
3.(3分)已知a,b,c,d是实数,且a﹣b>c﹣d,下列说法一定正确的是( )
A.若b=d,则a>c B.若a=c,则b>d
C.若b<d,则a>c D.若a>c,则b>d
4.(3分)关于x的不等式(a﹣3)x>a﹣3的解集是x>1,则a的取值范围是( )
A.a>3 B.a<3 C.a>1 D.a<1
5.(3分)如图,小手盖住的点的坐标可能为( )
A.(﹣1,﹣2) B.(﹣2,3) C.(2,0) D.(2,﹣3)
6.(3分)下列命题是假命题的是( )
A.“对顶角相等”的逆命题是假命题
B.在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c
C.两条平行线被第三条直线所截,内错角相等
D.同旁内角互补两直线平行
7.(3分)下列各式中,正确的是( )
A.4 B.± C.±± D.±4
8.(3分)把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
A.26° B.24° C.22° D.20°
9.(3分)圆圆读一本故事书,第一天读了全书的,第二天读了剩下的,这时还有36页没读,则她第二天读的页数为( )
A.18 B.16 C.36 D.12
10.(3分)课后延时服务已经落地,为了进一步对课后延时服务进行规范,某校计划在延时服务时间内开展各种社团活动.小明对全校学生进行抽样调查,收集整理拟参加社团活动类型(A.读书交流,B.体育锻炼,C.戏剧说唱,D.手工陶艺)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400
B.类型D所对应的扇形的圆心角为36
C.类型C所占的百分比为30%
D.类型B的人数为120人
11.(3分)某电梯乘载的质量超过300千克时会响起警示音,已知小华、小欧的体重分别为45千克、70千克.小华进入电梯,警示音没响,小欧在小华之后进入电梯,警示音响起.设电梯在两人进入前已乘载的质量为x千克,则x满足( )
A.185<x≤255 B.185≤x<255 C.230<x≤255 D.230≤x<255
12.(3分)如图,线段AB∥CD,AE∥CF,∠D﹣∠C=α,EP⊥AB于点P,EM平分∠AEB交AB于点M,则∠PEM的度数是( )
A. B. C.α D.2α
二.填空题(每小题3分,共18分)
13.(3分)如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC的度数是138°,第二次的拐角∠BCD的度数是 .
14.(3分)点(﹣5,3)到x轴上的距离是 .
15.(3分)某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛.在最近的10次选拔赛中,他们的成绩(单位:cm)折线统计图如图所示:
历届比赛成绩表明,成绩达到5.96m就很可能夺冠.若为了稳妥夺冠,则应选择参赛的运动员是 (填“甲”或“乙”).
16.(3分)已知关于x、y的二元一次方程组的解满足x﹣y>2,则m的最大整数值为m= .
17.(3分)如图,在由小正方形组成的网格图中,有a,b两户家用电路接入电表,a户电路接点与电表接入点之间所用电线长度为5m,则b户电路接点与电表接入点之间所用电线长度为 m.
18.(3分)若关于x的不等式组恰有3个整数解,则m的取值范围是 .
三.解答题(共46分)
19.计算:﹣12025﹣|1|+2cos30°+()﹣2.
20.解方程组:.
21.在平面直角坐标系中,△ABC经过平移得到三角形△A′B′C′,位置如图所示:
(1)分别写出点A、A'的坐标:A ,A' ;
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求△ABC的面积.
22.养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,教务处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A,B,C,D四组,如表所示.同时将调查结果绘制成下面两幅不完整的统计图.
请根据以上的信息,解答下列问题:
组别 早锻炼时间 频数(人数)
A 0≤x<10 10
B 10≤x<20 20
C 20≤x<30 a
D 30≤x<40 40
(1)此次抽样调查的样本容量是 ,a= ;
(2)补全频数分布直方图,扇形统计图D所在的圆心角的度数为 ;
(3)已知该校七年级共有1000名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.
23.“煎茶竹丝茄”是天府新区煎茶街道最为知名的农业特色产品,据考证,种植历史已有200余年,大规模种植和发展也有几十年历程.为推广当地特色农产品,某餐馆特推出鱼香茄子和炸茄盒两种特色菜,已知每份鱼香茄子的单价比炸茄盒的单价少6元,某天餐馆卖出46份鱼香茄子和36份炸茄盒共收入1200元.
(1)分别求出鱼香茄子和炸茄盒的单价;
(2)该餐馆计划“五一”劳动节当天推出鱼香茄子和炸茄盒共120份,为吸引更多食客,老板决定鱼香茄子降价两元,炸茄盒打八折销售,全部售完后希望收入不低于1530元,则炸茄盒最少应该售出多少份?
24.如图1,在平面直角坐标系中,点A的坐标为(0,8),点B在第一象限,△OAB为等边三角形.
(1)直接写出点B的纵坐标 ;
(2)如图2,OC⊥AB于点C,点C关于x轴的对称点为点D,则点D的纵坐标为 ;
(3)OC⊥AB于点C,点C关于x轴的对称点为点D,连接AD交OB于E,求OE的长.
2024-2025学年四川省绵阳市涪城区七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共12小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D B A A D B C B A C A
题号 12
答案 A
一.选择题(每小题3分,共36分)
1.(3分)的相反数是( )
A.5 B.0 C. D.
【解答】解:的相反数是:.
故选:D.
2.(3分)下列调查中,适合用普查方式的是( )
A.检测某城市空气质量
B.检测神舟十三号载人飞船的零部件质量情况
C.检测一批节能灯的使用寿命
D.检测某批次汽车的抗撞能力
【解答】解:A.检测某城市空气质量,适合抽样调查,故不符合题意;
B.检测神舟十三号载人飞船的零部件质量情况,适合普查,故符合题意;
C.检测一批节能灯的使用寿命,适合抽样调查,故不符合题意;
D.检测某批次汽车的抗撞能力,适合抽样调查,不符合题意.
故选:B.
3.(3分)已知a,b,c,d是实数,且a﹣b>c﹣d,下列说法一定正确的是( )
A.若b=d,则a>c B.若a=c,则b>d
C.若b<d,则a>c D.若a>c,则b>d
【解答】解:A、若b=d,a﹣b>c﹣d,则a>c,故此选项符合题意;
B、若a=c,a﹣b>c﹣d,则b<d,故此选项不符合题意;
C、若b<d,a﹣b>c﹣d,则a>c不一定成立,如a=1,c=3,b=2,d=5,故此选项不符合题意;
D、若a>c,a﹣b>c﹣d,则b>d不一定成立,有可能b=d,故此选项不符合题意;
故选:A.
4.(3分)关于x的不等式(a﹣3)x>a﹣3的解集是x>1,则a的取值范围是( )
A.a>3 B.a<3 C.a>1 D.a<1
【解答】解:∵关于x的不等式(a﹣3)x>a﹣3的解集是x>1,
∴a﹣3>0,
解得a>3.
故选:A.
5.(3分)如图,小手盖住的点的坐标可能为( )
A.(﹣1,﹣2) B.(﹣2,3) C.(2,0) D.(2,﹣3)
【解答】解:A.(﹣1,﹣2)在第三象限,故本选项不符合题意;
B.(﹣2,3)在第二象限,故本选项不符合题意;
C.(2,0)在x轴上,故本选项不符合题意;
D.(2,﹣3)在第四象限,故本选项符合题意.
故选:D.
6.(3分)下列命题是假命题的是( )
A.“对顶角相等”的逆命题是假命题
B.在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c
C.两条平行线被第三条直线所截,内错角相等
D.同旁内角互补两直线平行
【解答】解:“对顶角相等”的逆命题是“相等的角是对顶角“,逆命题为假命题,故A为真命题,不符合题意;
在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a⊥c,故B是假命题,符合题意;
两条平行线被第三条直线所截,内错角相等,故C是真命题,不符合题意;
同旁内角互补,两直线平行,故D是真命题,不符合题意;
故选:B.
7.(3分)下列各式中,正确的是( )
A.4 B.± C.±± D.±4
【解答】解:A、,本选项错误,
B、,本选项错误,
C、±±,本选项正确,
D、4,本选项错误,
故选:C.
8.(3分)把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
A.26° B.24° C.22° D.20°
【解答】解:如图,
∵直角三角板位于两条平行线间且∠1=54°,
∴∠3=126°,
又∵直角三角板含30°角,
∴180°﹣∠2﹣∠3=30°,
∴∠2=24°,
故选:B.
9.(3分)圆圆读一本故事书,第一天读了全书的,第二天读了剩下的,这时还有36页没读,则她第二天读的页数为( )
A.18 B.16 C.36 D.12
【解答】解:设这本故事书有x页,由题意得:
xx(xx)=36,
∴xxx=36,
∴x=36,
∴x=81,
∴(xx)(8181)=18.
故选:A.
10.(3分)课后延时服务已经落地,为了进一步对课后延时服务进行规范,某校计划在延时服务时间内开展各种社团活动.小明对全校学生进行抽样调查,收集整理拟参加社团活动类型(A.读书交流,B.体育锻炼,C.戏剧说唱,D.手工陶艺)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400
B.类型D所对应的扇形的圆心角为36
C.类型C所占的百分比为30%
D.类型B的人数为120人
【解答】解:样本容量为:100÷25%=400人,故选项A不合题意;
类型D所对应的扇形的圆心角为360°×10%=36°,故选项B不合题意;
类型C所占的百分比为:,故选项C符合题意;
类型B的人数为:400×(1﹣25%﹣10%﹣35%)=120(人),故选项D不合题意.
故选:C.
11.(3分)某电梯乘载的质量超过300千克时会响起警示音,已知小华、小欧的体重分别为45千克、70千克.小华进入电梯,警示音没响,小欧在小华之后进入电梯,警示音响起.设电梯在两人进入前已乘载的质量为x千克,则x满足( )
A.185<x≤255 B.185≤x<255 C.230<x≤255 D.230≤x<255
【解答】解:由题意得:,
解得:185<x≤255,
故选:A.
12.(3分)如图,线段AB∥CD,AE∥CF,∠D﹣∠C=α,EP⊥AB于点P,EM平分∠AEB交AB于点M,则∠PEM的度数是( )
A. B. C.α D.2α
【解答】解:∵AB∥CD,AE∥CF,
∴∠AEF=∠CFE,∠B=∠D(两直线平行,内错角相等),
∵∠CFE=∠D+∠C,∠D﹣∠C=α,
∴∠AEF=∠CFE=2∠C+α,∠D=∠B=∠C+α,
∴∠AEB=180°﹣2∠C﹣α,
∵EM平分∠AEB,
∴,
∵EP⊥AB,
∴∠EPB=90°,
∴∠PEB=90°﹣∠B=90°﹣∠C﹣α,
∴,
综上所述,只有选项A正确,符合题意,
故选:A.
二.填空题(每小题3分,共18分)
13.(3分)如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC的度数是138°,第二次的拐角∠BCD的度数是 138° .
【解答】解:AB∥CD,
∴∠BCD=∠ABC=138°.
故答案为:138°.
14.(3分)点(﹣5,3)到x轴上的距离是 3 .
【解答】解:点(﹣5,3)到x轴上的距离是|3|=3.
故答案为:3.
15.(3分)某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛.在最近的10次选拔赛中,他们的成绩(单位:cm)折线统计图如图所示:
历届比赛成绩表明,成绩达到5.96m就很可能夺冠.若为了稳妥夺冠,则应选择参赛的运动员是 甲 (填“甲”或“乙”).
【解答】解:∵甲成绩由小到大排列为:585,596,597,598,600,601,604,610,612,613,
∴甲成绩的中位数为:(600+601)÷2=600.5(cm),
甲成绩的平均数为:(585+596+597+598+600=601+604+610+612+613)÷10=601.6(分);
∵乙成绩由小到大排列为:574,580,585,590,593,598,613,618,618,624,
∴乙成绩的中位数为:(593+598)÷2=595.5(cm),
乙成绩的平均数为:(574+580+585+590+593+598+613+618+618+624)÷10=599.3(cm),
∵甲成绩的平均数高于乙平均数,甲成绩的中位数高于乙中位数,从折线统计图可以看出甲的成绩波动较小,且甲10次成绩中有9次达到夺冠的成绩,乙只有5次达到夺冠的成绩,
∴应选择参赛的运动员是:甲.
故答案为:甲.
16.(3分)已知关于x、y的二元一次方程组的解满足x﹣y>2,则m的最大整数值为m= ﹣2 .
【解答】解:,
由②﹣①得:x﹣y=1﹣m,
∵x﹣y>2,
∴1﹣m>2,
∴m<﹣1,
m的最大整数值为﹣2.
故答案为:﹣2.
17.(3分)如图,在由小正方形组成的网格图中,有a,b两户家用电路接入电表,a户电路接点与电表接入点之间所用电线长度为5m,则b户电路接点与电表接入点之间所用电线长度为 5 m.
【解答】解:由平移可知,
a,b两户的电线竖直方向和水平方向的长度相同,
所以b户电路接点与电表接入点之间的电线长度为5m.
故答案为:5.
18.(3分)若关于x的不等式组恰有3个整数解,则m的取值范围是 4<m≤5 .
【解答】解:.
解①得,x<m.
解②得,x≥2.
∴不等式组的解集为2≤x<m.
∵不等式组有3个整数解.
∴这3个整数解为:2,3,4.
∴m的取值范围为:4<m≤5.
故答案为:4<m≤5.
三.解答题(共46分)
19.计算:﹣12025﹣|1|+2cos30°+()﹣2.
【解答】解:原式=﹣1﹣(1)+24
=﹣114
=4.
20.解方程组:.
【解答】解:整理得,
①×2得,10x﹣4y=6③,
③﹣②得7x=7,
解得x=1,
将x=1代入①得5×1﹣2y=3,
解得y=1,
所以方程组的解为.
21.在平面直角坐标系中,△ABC经过平移得到三角形△A′B′C′,位置如图所示:
(1)分别写出点A、A'的坐标:A (1,0) ,A' (﹣4,4) ;
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为 (m﹣5,n+4) ;
(3)求△ABC的面积.
【解答】解:(1)由图知A(1,0),A'(﹣4,4);
(2)A(1,0)对应点的对应点A′(﹣4,4)得A向左平移5个单位,向上平移4个单位得到A′,
故△ABC内M(m,n)平移后对应点M'的坐标为(m﹣5,n+4);
(3)△ABC的面积为:4×44×23×21×4=7.
22.养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,教务处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A,B,C,D四组,如表所示.同时将调查结果绘制成下面两幅不完整的统计图.
请根据以上的信息,解答下列问题:
组别 早锻炼时间 频数(人数)
A 0≤x<10 10
B 10≤x<20 20
C 20≤x<30 a
D 30≤x<40 40
(1)此次抽样调查的样本容量是 200 ,a= 130 ;
(2)补全频数分布直方图,扇形统计图D所在的圆心角的度数为 72° ;
(3)已知该校七年级共有1000名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.
【解答】解:(1)10÷5%=200(人),a=200﹣10﹣20﹣40=130,
故答案为:200,130;
(2)补全频数分布直方图如下:
扇形D所对应的圆心角度数为:360°72°,
故答案为:72°;
(3)1000850(人),
答:该校七年级1000名学生中约有850人一天早锻炼的时间不少于20分钟.
23.“煎茶竹丝茄”是天府新区煎茶街道最为知名的农业特色产品,据考证,种植历史已有200余年,大规模种植和发展也有几十年历程.为推广当地特色农产品,某餐馆特推出鱼香茄子和炸茄盒两种特色菜,已知每份鱼香茄子的单价比炸茄盒的单价少6元,某天餐馆卖出46份鱼香茄子和36份炸茄盒共收入1200元.
(1)分别求出鱼香茄子和炸茄盒的单价;
(2)该餐馆计划“五一”劳动节当天推出鱼香茄子和炸茄盒共120份,为吸引更多食客,老板决定鱼香茄子降价两元,炸茄盒打八折销售,全部售完后希望收入不低于1530元,则炸茄盒最少应该售出多少份?
【解答】解:(1)设鱼香茄子的单价为x元,炸茄盒的单价为y元,
由题意得:,
解得:,
答:鱼香茄子的单价为12元,炸茄盒的单价为18元;
(2)设炸茄盒应该售出m份,则鱼香茄子应该售出(120﹣m)份,
由题意得:(12﹣2)(120﹣m)+18×0.8m≥1530,
解得:m≥75,
答:炸茄盒最少应该售出75份.
24.如图1,在平面直角坐标系中,点A的坐标为(0,8),点B在第一象限,△OAB为等边三角形.
(1)直接写出点B的纵坐标 (4,4) ;
(2)如图2,OC⊥AB于点C,点C关于x轴的对称点为点D,则点D的纵坐标为 ﹣6 ;
(3)OC⊥AB于点C,点C关于x轴的对称点为点D,连接AD交OB于E,求OE的长.
【解答】解:(1)如图1,过点B作BH⊥AO于H,
∵点A的坐标为(0,8),
∴OA=8,
∵△OAB为等边三角形,BH⊥AO,
∴AO=BO=AB=8,AH=OH=4,
∴BH4,
∴点B(4,4),
故答案为:(4,4);
(2)过点B作BH⊥AO于H,过点C作CG⊥AO于G,连接CH,连接CD交BO于N,
∵OC⊥AB,△OAB是等边三角形,
∴AC=BC,
∵BH⊥AO,
∴CH=AC=BC=4,
又∵CG⊥AH,
∴AG=GH=2,
∴OG=6,
∴点C的纵坐标为6,
∵点C关于x轴的对称点为点D,
∴点D的纵坐标﹣6;
故答案为:﹣6;
(3)∵CD⊥x轴,
∴CD=12,CD∥AO,
∴∠D=∠OAE,∠BCN=∠BAO=60°,∠BNC=∠AOB=60°,
∴△CNB是等边三角形,
∴CN=BC=4=BN=ON,
∴ND=8=AO,
又∵∠AEO=∠DEN,
∴△AEO≌△DEN(AAS),
∴OE=ENON=2.
同课章节目录
