14.2三角板---转角遇到全等教学设计 沪科版(2024)数学八年级上册
文档属性
| 名称 | 14.2三角板---转角遇到全等教学设计 沪科版(2024)数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 237.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 07:25:01 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 三角板---转角遇到全等
教科书 书 名:沪科版教材 出版社: 上海科技出版社 出版日期:2025年5月
教学目标
1.三角形全等的判定; 2、分类讨论、探究解法共性规律,形成技能; 3.在解决问题的过程当中,培养学生观察,分析能力,熟练进行分类,并找出各类情形中共性规律,形成解题技能。 4.学生培养乐于动手、敢于辨析、善于思考、勇于回答的学习精神。
教学重难点
教学重点: 1、三角形全等的判定 2、分类讨论、探究解法共性规律
教学难点: 分类讨论、探究解法共性规律,形成技能。
教学过程
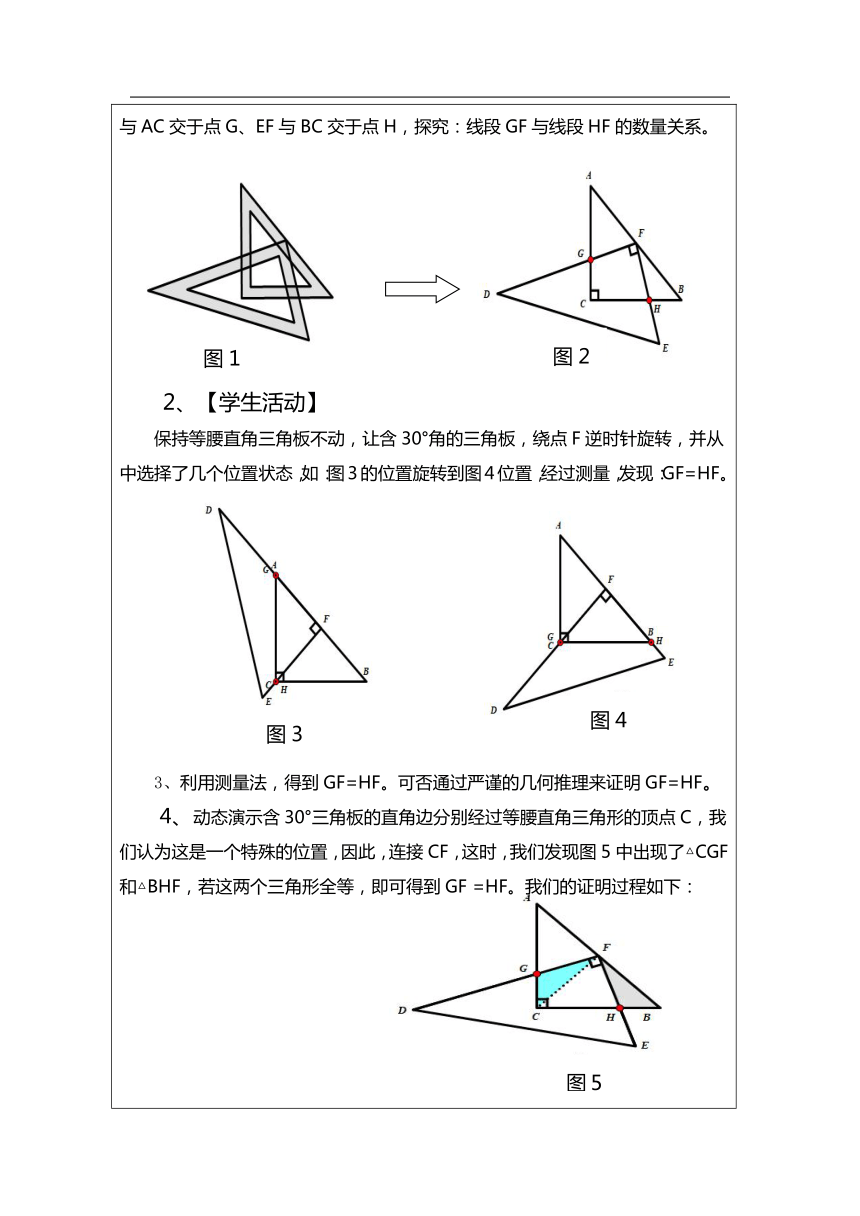
基本情况 学生三角板是学生熟悉的学习用品,也是探究某些数学问题的好用具。 在数学沪科版七年级下册时,学生可以利用三角板,通过对三角板的旋转,确定边平行时,对应角度的大小,并学会对边平行的情况进行分类讨论,学会分析,形成分类讨论的意识,掌握分类的方法。在八年级上册,几何知识库中又多了全等这一概念,同学们也可以在三角板旋转的过程中,分类寻找全等的三角形,并对三角形的全等做出严谨的推理证明,对比各种情形下三角形全等的判定理由,找出其中的规律,形成解题技能。 在解决问题的过程中,应用三角形全等的判定方法、等量代换等数学知识,这些可以增强学生几何推理能力,更能在具体的情境问题中,培养学生分类意识讨论,感受各类别之间的联系和规律,增强学生由实验猜想到推理论证的活动经验,用数学的眼光看待周围的事物,用积极的态度去思考问题,探究规律,形成技能。 二、教学与活动过程 (一)准备工作 1、一副三角板 ,利用这对三角板探究全等。 2、已掌握判定三角形全等方法有: 边角边(SAS)、角边角(ASA)、角角边(AAS)、边边边(SSS) 直角三角形还有一种特殊的判定方法:斜边直角边(HL) 3、【设计意图】 回顾有关的知识点,为本节课做好准备工作。 提出问题 1、【教师活动】 如图1,将含30°的直角三角形的直角顶点放在等腰直角三角斜边的中点处,其两条直角边分别与等腰直角三角形的两条直角边相交。抽象出如图2所示的几何图形,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,F是AB的中点 ,DF与AC交于点G、EF与BC交于点H,探究:线段GF与线段HF的数量关系。 【学生活动】 保持等腰直角三角板不动,让含30°角的三角板,绕点F逆时针旋转,并从中选择了几个位置状态,如:图3的位置旋转到图4位置,经过测量,发现:GF=HF。 利用测量法,得到GF=HF。可否通过严谨的几何推理来证明GF=HF。 4、动态演示含30°三角板的直角边分别经过等腰直角三角形的顶点C,我们认为这是一个特殊的位置,因此,连接CF,这时,我们发现图5中出现了△CGF和△BHF,若这两个三角形全等,即可得到GF =HF。我们的证明过程如下: 证明:连接CF ∵∠1+∠2=90°,∠2+∠3=90° ∴∠1=∠3(同角的余角相等) ∵在等腰Rt△ABC中,AC=BC,F是AB的中点 ∴在△CGF和△BHF中:∠1=∠3,CF=BF,∠GCF=∠FBH=45° ∴△CGF≌△BHF(ASA) ∴GF=HF 【继续探究】 如果将△DEF绕F点旋转出图6、图7,图8的位置,G点成为边AC、DF所在直线的交点,H点成为边BC、EF所在直线的交点,还会有GF=HF吗? 图6 图 7 图8 【设计意图】学会分析动态的几何问题,掌握图形的运动状态,并能画出对应的几何图形,培养学生抽象思维能力;从测量法的直观感知到严谨的几何推理,培养学生运用“猜想-验证”的思维方式解答问题。 深入探究 【学生活动】 将△DEF绕点F逆时针旋转一周,找出了三种不同的位置状态,如图6、7、8。可以发现了一个有趣的现象:都可以通过证明△CGF和△BHF全等,来说明GF=HF,而△CGF和△BHF全等,都可以用ASA来证明,都是∠GFC=∠HFB,CF=BF,∠GCF=∠FBH,只是在不同的情况下,角度的大小有所变化: 图6 图 7 图8 在图6中, ∠GFC和∠HFB位置变化了,但是, ∵∠CFH-∠GFC=90°,∠CFH-∠HFB=90°∴∠GFC=∠HFB(等量代换) ∠GCF和∠FBH变大了,但是,∠GCF=∠FBH=135° 在图7中:∠GFC和∠HFB变大了,但是, ∵∠GFC-∠CFH=90°,∠HFB-∠CFH=90°∴∠GFC=∠HFB(等量代换) ∠GCF和∠FBH位置变了,但是,∠GCF=∠FBH=45° 在图8中,所有等量关系证明和图6的一样。 这真是非常有趣的证明过程,只要沿着第一种情况的证明思路,其中所涉及的角的名称没变,角的位置虽略有改变,但按名称中的字母顺序,还是很容易锁定的,角度数变化也只限于变成原来角的补角或者原来两角和关系变成两角差关系。这题中所涉及的线段,长度和位置都没有变化,这真是太神奇了!我们这组给这种有规律的证明方法起个名字,不妨叫做“顺藤摸瓜追踪法”。 【设计意图】培养学生进行分类讨论的意识和能力,并在解答各分类情景的过程中,发现解答方法之间的关联,总结解决问题的规律,形成解答技能。
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 三角板---转角遇到全等
教科书 书 名:沪科版教材 出版社: 上海科技出版社 出版日期:2025年5月
教学目标
1.三角形全等的判定; 2、分类讨论、探究解法共性规律,形成技能; 3.在解决问题的过程当中,培养学生观察,分析能力,熟练进行分类,并找出各类情形中共性规律,形成解题技能。 4.学生培养乐于动手、敢于辨析、善于思考、勇于回答的学习精神。
教学重难点
教学重点: 1、三角形全等的判定 2、分类讨论、探究解法共性规律
教学难点: 分类讨论、探究解法共性规律,形成技能。
教学过程
基本情况 学生三角板是学生熟悉的学习用品,也是探究某些数学问题的好用具。 在数学沪科版七年级下册时,学生可以利用三角板,通过对三角板的旋转,确定边平行时,对应角度的大小,并学会对边平行的情况进行分类讨论,学会分析,形成分类讨论的意识,掌握分类的方法。在八年级上册,几何知识库中又多了全等这一概念,同学们也可以在三角板旋转的过程中,分类寻找全等的三角形,并对三角形的全等做出严谨的推理证明,对比各种情形下三角形全等的判定理由,找出其中的规律,形成解题技能。 在解决问题的过程中,应用三角形全等的判定方法、等量代换等数学知识,这些可以增强学生几何推理能力,更能在具体的情境问题中,培养学生分类意识讨论,感受各类别之间的联系和规律,增强学生由实验猜想到推理论证的活动经验,用数学的眼光看待周围的事物,用积极的态度去思考问题,探究规律,形成技能。 二、教学与活动过程 (一)准备工作 1、一副三角板 ,利用这对三角板探究全等。 2、已掌握判定三角形全等方法有: 边角边(SAS)、角边角(ASA)、角角边(AAS)、边边边(SSS) 直角三角形还有一种特殊的判定方法:斜边直角边(HL) 3、【设计意图】 回顾有关的知识点,为本节课做好准备工作。 提出问题 1、【教师活动】 如图1,将含30°的直角三角形的直角顶点放在等腰直角三角斜边的中点处,其两条直角边分别与等腰直角三角形的两条直角边相交。抽象出如图2所示的几何图形,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,F是AB的中点 ,DF与AC交于点G、EF与BC交于点H,探究:线段GF与线段HF的数量关系。 【学生活动】 保持等腰直角三角板不动,让含30°角的三角板,绕点F逆时针旋转,并从中选择了几个位置状态,如:图3的位置旋转到图4位置,经过测量,发现:GF=HF。 利用测量法,得到GF=HF。可否通过严谨的几何推理来证明GF=HF。 4、动态演示含30°三角板的直角边分别经过等腰直角三角形的顶点C,我们认为这是一个特殊的位置,因此,连接CF,这时,我们发现图5中出现了△CGF和△BHF,若这两个三角形全等,即可得到GF =HF。我们的证明过程如下: 证明:连接CF ∵∠1+∠2=90°,∠2+∠3=90° ∴∠1=∠3(同角的余角相等) ∵在等腰Rt△ABC中,AC=BC,F是AB的中点 ∴在△CGF和△BHF中:∠1=∠3,CF=BF,∠GCF=∠FBH=45° ∴△CGF≌△BHF(ASA) ∴GF=HF 【继续探究】 如果将△DEF绕F点旋转出图6、图7,图8的位置,G点成为边AC、DF所在直线的交点,H点成为边BC、EF所在直线的交点,还会有GF=HF吗? 图6 图 7 图8 【设计意图】学会分析动态的几何问题,掌握图形的运动状态,并能画出对应的几何图形,培养学生抽象思维能力;从测量法的直观感知到严谨的几何推理,培养学生运用“猜想-验证”的思维方式解答问题。 深入探究 【学生活动】 将△DEF绕点F逆时针旋转一周,找出了三种不同的位置状态,如图6、7、8。可以发现了一个有趣的现象:都可以通过证明△CGF和△BHF全等,来说明GF=HF,而△CGF和△BHF全等,都可以用ASA来证明,都是∠GFC=∠HFB,CF=BF,∠GCF=∠FBH,只是在不同的情况下,角度的大小有所变化: 图6 图 7 图8 在图6中, ∠GFC和∠HFB位置变化了,但是, ∵∠CFH-∠GFC=90°,∠CFH-∠HFB=90°∴∠GFC=∠HFB(等量代换) ∠GCF和∠FBH变大了,但是,∠GCF=∠FBH=135° 在图7中:∠GFC和∠HFB变大了,但是, ∵∠GFC-∠CFH=90°,∠HFB-∠CFH=90°∴∠GFC=∠HFB(等量代换) ∠GCF和∠FBH位置变了,但是,∠GCF=∠FBH=45° 在图8中,所有等量关系证明和图6的一样。 这真是非常有趣的证明过程,只要沿着第一种情况的证明思路,其中所涉及的角的名称没变,角的位置虽略有改变,但按名称中的字母顺序,还是很容易锁定的,角度数变化也只限于变成原来角的补角或者原来两角和关系变成两角差关系。这题中所涉及的线段,长度和位置都没有变化,这真是太神奇了!我们这组给这种有规律的证明方法起个名字,不妨叫做“顺藤摸瓜追踪法”。 【设计意图】培养学生进行分类讨论的意识和能力,并在解答各分类情景的过程中,发现解答方法之间的关联,总结解决问题的规律,形成解答技能。
