10.2平行线的判定 教学设计 沪科版(2024)数学七年级下册
文档属性
| 名称 | 10.2平行线的判定 教学设计 沪科版(2024)数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 205.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 00:00:00 | ||
图片预览

文档简介
10.2 平行线的判定
第2课时 同位角、内错角和同旁内角
学习目标:
1.了解同位角、内错角和同旁内角的概念.
2.会识别由“三线八角”构成的同位角、内错角和同旁内角.
3.经历观察、操作、想象、推理、交流等活动,进一步发展空间想象、推理能力和有条理的表达能力.
4.在积极参与探索、交流的数学活动中,体验数学与实际生活的密切联系,激发学生的求知欲,感受与他人合作的重要性.
教学重难点:
能够运用“三线八角”解决实际问题.
教学过程:
一、复习回顾
过点B画直线a的平行线,说一说你是怎样画的?能画几条直线?
B.
a
①“一重合”:三角板的一边与已知直线重合;
②“二靠紧”:把直尺靠紧三角板的另一边;
③“三移动”:沿直尺移动三角板,使三角板与直线重合的边过已知点;
④“四画线”:沿三角板过已知点的边画直线。
结论:有且只有一条。
二、探究新知
探究1:画平行线时,在三角尺移动的过程中,直尺起着“基准线”的作用.“基准线”与三角尺上边夹角始终不变.
研究同一平面内两条直线是否平行,同样也需要一条“基准线”
探究2:如图,两条直线被第三条直线(相当于“基准线”)所截。
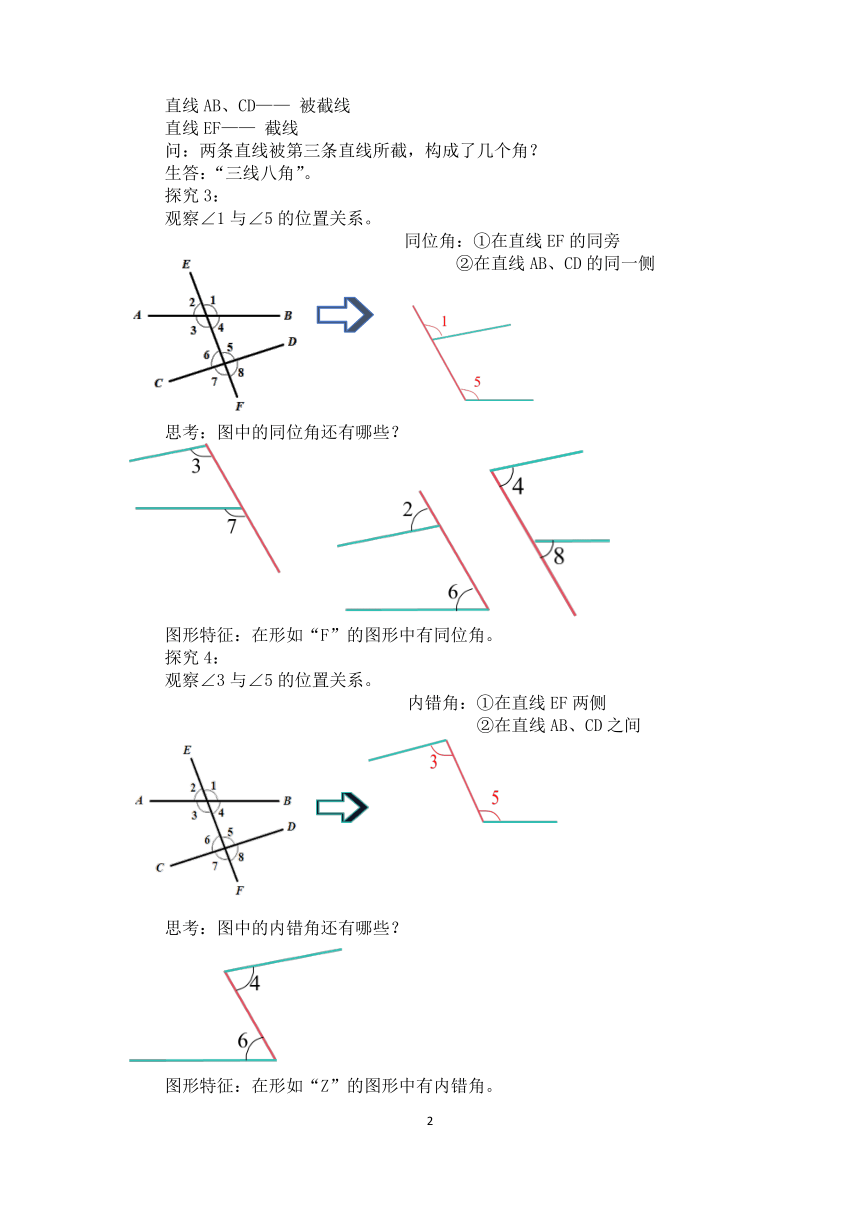
两条直线AB、CD被第三条直线EF所截.
直线AB、CD—— 被截线
直线EF—— 截线
问:两条直线被第三条直线所截,构成了几个角?
生答:“三线八角”。
探究3:
观察∠1与∠5的位置关系。
同位角:①在直线EF的同旁
②在直线AB、CD的同一侧
思考:图中的同位角还有哪些?
图形特征:在形如“F”的图形中有同位角。
探究4:
观察∠3与∠5的位置关系。
内错角:①在直线EF两侧
②在直线AB、CD之间
思考:图中的内错角还有哪些?
图形特征:在形如“Z”的图形中有内错角。
探究5:
观察∠4与∠5的位置关系。
同旁内角: ①在直线EF同旁
②在直线AB、CD之间
思考:图中的同旁内角还有哪些?
图形特征:在形如“U”的图形中有同旁内角。
归纳:
同位角、内错角和同旁内角的结构特征。
截线 被截线 结构特征
同位角 同旁 同侧 F
内错角 两侧 之间 Z
同旁内角 同旁 之间 U
三、应用新知:
例1 根据图形填空:
(1)若直线ED,BF被直线AB所截,则∠1和______是同位角;
(2)若直线ED,BF被直线AF所截,则∠3和_____是内错角;
(3)∠1和∠3是直线AB,AF 被直线____所截构成的内错角;
(4)∠2和∠5是直线 AB,_____被直线 BF 所截构成的________角.
分析:(1)(2)根据同位角和内错角的特征,得出答案即可。
答案:∠2,∠4
分析:(3)(4)根据内错角和同旁内角的特征,得出答案即可。
答案:ED,AF,同旁内。
例2 如图,直线DE,BC被直线AB所截.∠1与∠2,∠1与∠3,∠1与∠4各是什么角?
解:∠1与∠2是内错角,
∠1与∠3是同旁内角,
∠1与∠4是同位角。
四、课堂练习
1. 如图,直线AB,CD被直线CE所截,与∠1成内错角的是______;
与∠1成同旁内角的是______;直线AB,CD被直线DE所截,与∠2成内错角的是______;与∠2成同旁内角的是______.
答案:∠3,∠BEC,∠5,∠AED.
2.如图,∠1与∠D,∠1与∠B,∠3与∠4,∠B与∠BCD,∠2与∠4分别是哪两条直线被哪一条直线所截得到的?它们中的每一对角分别叫做什么角?
解:∠1与∠D是直线AB与CD被直线AD所截得到的内错角;
∠1与∠B是直线AD与BC被直线AB所截得到的同位角;
∠3与∠4是直线AB与CD被直线AC所截得到的内错角;
∠B与∠BCD是直线AB与CD被直线BC所截得到的同旁内角;
∠2与∠4是直线AD与CD被直线AC所截得到的同旁内角.
五、归纳总结
六、板书
10.2平行线的判定(第2课时)
三线八角
同位角、内错角和同旁内角
截线 被截线 结构特征
同位角 同旁 同侧 F
内错角 两侧 之间 Z
同旁内角 同旁 之间 U
5
第2课时 同位角、内错角和同旁内角
学习目标:
1.了解同位角、内错角和同旁内角的概念.
2.会识别由“三线八角”构成的同位角、内错角和同旁内角.
3.经历观察、操作、想象、推理、交流等活动,进一步发展空间想象、推理能力和有条理的表达能力.
4.在积极参与探索、交流的数学活动中,体验数学与实际生活的密切联系,激发学生的求知欲,感受与他人合作的重要性.
教学重难点:
能够运用“三线八角”解决实际问题.
教学过程:
一、复习回顾
过点B画直线a的平行线,说一说你是怎样画的?能画几条直线?
B.
a
①“一重合”:三角板的一边与已知直线重合;
②“二靠紧”:把直尺靠紧三角板的另一边;
③“三移动”:沿直尺移动三角板,使三角板与直线重合的边过已知点;
④“四画线”:沿三角板过已知点的边画直线。
结论:有且只有一条。
二、探究新知
探究1:画平行线时,在三角尺移动的过程中,直尺起着“基准线”的作用.“基准线”与三角尺上边夹角始终不变.
研究同一平面内两条直线是否平行,同样也需要一条“基准线”
探究2:如图,两条直线被第三条直线(相当于“基准线”)所截。
两条直线AB、CD被第三条直线EF所截.
直线AB、CD—— 被截线
直线EF—— 截线
问:两条直线被第三条直线所截,构成了几个角?
生答:“三线八角”。
探究3:
观察∠1与∠5的位置关系。
同位角:①在直线EF的同旁
②在直线AB、CD的同一侧
思考:图中的同位角还有哪些?
图形特征:在形如“F”的图形中有同位角。
探究4:
观察∠3与∠5的位置关系。
内错角:①在直线EF两侧
②在直线AB、CD之间
思考:图中的内错角还有哪些?
图形特征:在形如“Z”的图形中有内错角。
探究5:
观察∠4与∠5的位置关系。
同旁内角: ①在直线EF同旁
②在直线AB、CD之间
思考:图中的同旁内角还有哪些?
图形特征:在形如“U”的图形中有同旁内角。
归纳:
同位角、内错角和同旁内角的结构特征。
截线 被截线 结构特征
同位角 同旁 同侧 F
内错角 两侧 之间 Z
同旁内角 同旁 之间 U
三、应用新知:
例1 根据图形填空:
(1)若直线ED,BF被直线AB所截,则∠1和______是同位角;
(2)若直线ED,BF被直线AF所截,则∠3和_____是内错角;
(3)∠1和∠3是直线AB,AF 被直线____所截构成的内错角;
(4)∠2和∠5是直线 AB,_____被直线 BF 所截构成的________角.
分析:(1)(2)根据同位角和内错角的特征,得出答案即可。
答案:∠2,∠4
分析:(3)(4)根据内错角和同旁内角的特征,得出答案即可。
答案:ED,AF,同旁内。
例2 如图,直线DE,BC被直线AB所截.∠1与∠2,∠1与∠3,∠1与∠4各是什么角?
解:∠1与∠2是内错角,
∠1与∠3是同旁内角,
∠1与∠4是同位角。
四、课堂练习
1. 如图,直线AB,CD被直线CE所截,与∠1成内错角的是______;
与∠1成同旁内角的是______;直线AB,CD被直线DE所截,与∠2成内错角的是______;与∠2成同旁内角的是______.
答案:∠3,∠BEC,∠5,∠AED.
2.如图,∠1与∠D,∠1与∠B,∠3与∠4,∠B与∠BCD,∠2与∠4分别是哪两条直线被哪一条直线所截得到的?它们中的每一对角分别叫做什么角?
解:∠1与∠D是直线AB与CD被直线AD所截得到的内错角;
∠1与∠B是直线AD与BC被直线AB所截得到的同位角;
∠3与∠4是直线AB与CD被直线AC所截得到的内错角;
∠B与∠BCD是直线AB与CD被直线BC所截得到的同旁内角;
∠2与∠4是直线AD与CD被直线AC所截得到的同旁内角.
五、归纳总结
六、板书
10.2平行线的判定(第2课时)
三线八角
同位角、内错角和同旁内角
截线 被截线 结构特征
同位角 同旁 同侧 F
内错角 两侧 之间 Z
同旁内角 同旁 之间 U
5
