1-3 动量守恒定律在碰撞中的应用 课件
文档属性
| 名称 | 1-3 动量守恒定律在碰撞中的应用 课件 | 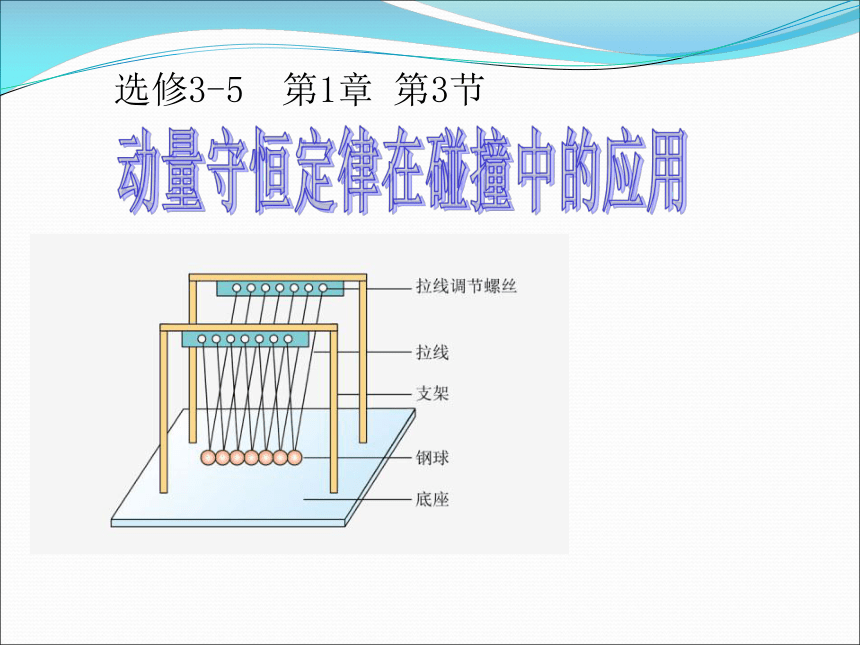 | |
| 格式 | zip | ||
| 文件大小 | 292.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 广东版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-07-09 10:44:57 | ||
图片预览






文档简介
课件14张PPT。动量守恒定律在碰撞中的应用 选修3-5 第1章 第3节 知识要点复习:
1. 碰撞的种类________、_________ 、_________
2.动量守恒定律:____________________________
__________________________________
3.动量守恒定律成立的条件
⑴系统 或者所受外力之和为零;
⑵系统受外力,但外力 内力,可以忽略;
⑶系统在 所受的合外力为零,则该方向
上动量守恒。
4.动量守恒定律的表达形式
(1) 即p1+p2=p1′+p2′,
(2) ,即Δp1= -Δp2 系统受到的合外力为零, 则系统的总动量保持不变。
不受合外力远小于某一直线上弹性碰撞,非弹性碰撞,完全非弹性碰撞 例1:在列车编组站里,一辆载重质m1=3.0×104kg的货车在平直的轨道上以v1=2m/s的速度运动,碰上另一辆载重后质量为m2=4.5×104 Kg的静止的货车,他们碰撞后结合在一起继续运动,求运动的速度。分析:
(1)研究对象是什么?
(2)该系统受到的力有哪些,动量是否守恒?
(3)系统的初、末动量如何表示?一. 动量守恒定律在完全非弹性碰撞中的应用解;以碰撞前货车的运动方向为正,则有=2m/s.设两车碰撞后的速度为,两车的碰撞前的初总动量 p=m1v1,碰后的总动量p=(m1+m2)v′. 由动量守恒定律p=p′可得:
m1v1=(m1+m2)v′
V′>0表示两车碰撞后的速度方向与初速度方向一致
总结归纳应用动量守恒定律解决问题的基本思路和一般方法:
A.分析初、末态的总动量
B.列出方程求解
C.确定正方向
D.判断是否守恒
E.确定研究对象(系统)
请按正确的步骤排序:_______________ EDCAB变式训练1:
抛出的手雷在最高点时水平速度为20m/s,这时忽然炸成两块,其中大块质量300g仍按原方向飞行,其速度测得为100m/s,另一小块质量为200g,求它在水平方向的速度的大小和方向。v1 解:以爆炸前的速度vo为正方向,由动量守恒定律得:
mv0=m1v1+m2v2
V2=(mv0-m1v1)/m2
将数据带入得:
v2=(0.5×20-0.3×100)/0.2m/s
=-100m/s
即速度方向与正方向相反,大小为 100m/s
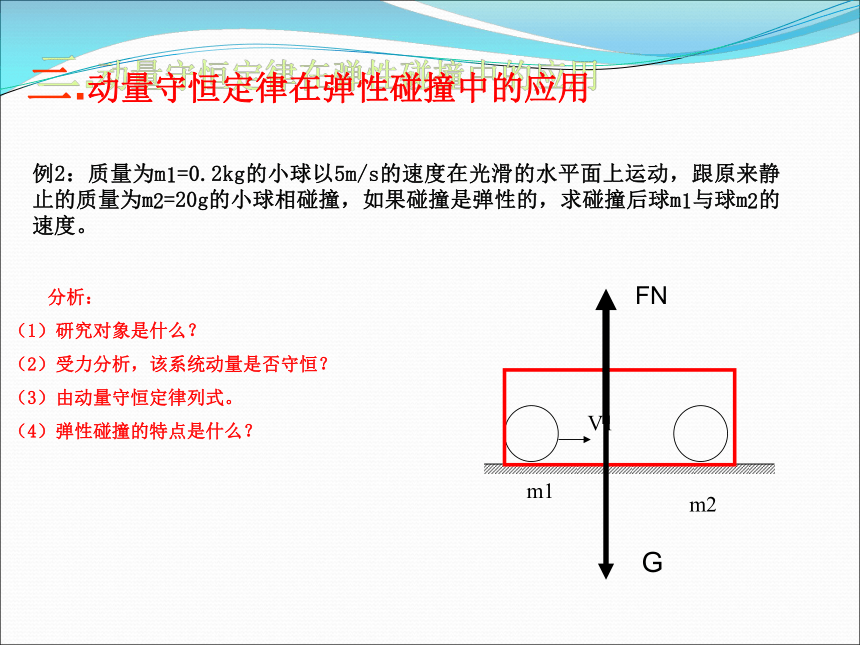
V2?例2:质量为m1=0.2kg的小球以5m/s的速度在光滑的水平面上运动,跟原来静止的质量为m2=20g的小球相碰撞,如果碰撞是弹性的,求碰撞后球m1与球m2的速度。二.动量守恒定律在弹性碰撞中的应用 分析:
(1)研究对象是什么?
(2)受力分析,该系统动量是否守恒?
(3)由动量守恒定律列式。
(4)弹性碰撞的特点是什么?
设碰撞前m1速度为v1 ,碰撞后m1速度变为v1 ′m2的速度为 v2 ′ 。以v1的方向为正,则:动量守恒:机械能守恒:由(1)(2)式可以解出:碰撞过程中单个小球的合力是否变化?
能否用牛顿运动定律求解?
动量守恒定律优点:(1)动量守恒定律只需考虑过程的初,末状态,
不必涉及过程 的细节.
(2)能用于计算物体在变力下的运动情况.应用范围广.变式训练2:
两个完全相同的小钢球在光滑的水平面上分别以3m/s和5m/s的速率相向运动,求它们发生弹性正碰后的速度v1′和v2′。
解:
以v1的方向为正,碰撞前两球的速度分别为v1= 3m/s v2=-5m/s ,碰撞后速度变为v1 ′、v2 ′则
动量守恒:
机械能守恒得
联立上式解得:
两球m1,m2对心碰撞,碰撞前速度分别为v10 、v20,求碰撞后速度。
动量守恒:机械能守恒:由(1)(2)式
可以解出2 特例:质量相等的两物体发生弹性正碰小结1.利用动量守恒的解题步骤:
(1).确定研究对象(系统) (2).判断是否守恒 (3).确定正方向 (4).分析初、末态的总动量 (5)..列出方程求解 2.动量守恒定律的优点:
(1)可用于物体在变力作用下的运动情况
(2)只需考虑初、末状态,不需考虑细节
(3)应用范围更广泛3. 碰撞中动量守恒与系统的能量(动能)守恒的运用。作业:
课本12页第1题,第4题
1. 碰撞的种类________、_________ 、_________
2.动量守恒定律:____________________________
__________________________________
3.动量守恒定律成立的条件
⑴系统 或者所受外力之和为零;
⑵系统受外力,但外力 内力,可以忽略;
⑶系统在 所受的合外力为零,则该方向
上动量守恒。
4.动量守恒定律的表达形式
(1) 即p1+p2=p1′+p2′,
(2) ,即Δp1= -Δp2 系统受到的合外力为零, 则系统的总动量保持不变。
不受合外力远小于某一直线上弹性碰撞,非弹性碰撞,完全非弹性碰撞 例1:在列车编组站里,一辆载重质m1=3.0×104kg的货车在平直的轨道上以v1=2m/s的速度运动,碰上另一辆载重后质量为m2=4.5×104 Kg的静止的货车,他们碰撞后结合在一起继续运动,求运动的速度。分析:
(1)研究对象是什么?
(2)该系统受到的力有哪些,动量是否守恒?
(3)系统的初、末动量如何表示?一. 动量守恒定律在完全非弹性碰撞中的应用解;以碰撞前货车的运动方向为正,则有=2m/s.设两车碰撞后的速度为,两车的碰撞前的初总动量 p=m1v1,碰后的总动量p=(m1+m2)v′. 由动量守恒定律p=p′可得:
m1v1=(m1+m2)v′
V′>0表示两车碰撞后的速度方向与初速度方向一致
总结归纳应用动量守恒定律解决问题的基本思路和一般方法:
A.分析初、末态的总动量
B.列出方程求解
C.确定正方向
D.判断是否守恒
E.确定研究对象(系统)
请按正确的步骤排序:_______________ EDCAB变式训练1:
抛出的手雷在最高点时水平速度为20m/s,这时忽然炸成两块,其中大块质量300g仍按原方向飞行,其速度测得为100m/s,另一小块质量为200g,求它在水平方向的速度的大小和方向。v1 解:以爆炸前的速度vo为正方向,由动量守恒定律得:
mv0=m1v1+m2v2
V2=(mv0-m1v1)/m2
将数据带入得:
v2=(0.5×20-0.3×100)/0.2m/s
=-100m/s
即速度方向与正方向相反,大小为 100m/s
V2?例2:质量为m1=0.2kg的小球以5m/s的速度在光滑的水平面上运动,跟原来静止的质量为m2=20g的小球相碰撞,如果碰撞是弹性的,求碰撞后球m1与球m2的速度。二.动量守恒定律在弹性碰撞中的应用 分析:
(1)研究对象是什么?
(2)受力分析,该系统动量是否守恒?
(3)由动量守恒定律列式。
(4)弹性碰撞的特点是什么?
设碰撞前m1速度为v1 ,碰撞后m1速度变为v1 ′m2的速度为 v2 ′ 。以v1的方向为正,则:动量守恒:机械能守恒:由(1)(2)式可以解出:碰撞过程中单个小球的合力是否变化?
能否用牛顿运动定律求解?
动量守恒定律优点:(1)动量守恒定律只需考虑过程的初,末状态,
不必涉及过程 的细节.
(2)能用于计算物体在变力下的运动情况.应用范围广.变式训练2:
两个完全相同的小钢球在光滑的水平面上分别以3m/s和5m/s的速率相向运动,求它们发生弹性正碰后的速度v1′和v2′。
解:
以v1的方向为正,碰撞前两球的速度分别为v1= 3m/s v2=-5m/s ,碰撞后速度变为v1 ′、v2 ′则
动量守恒:
机械能守恒得
联立上式解得:
两球m1,m2对心碰撞,碰撞前速度分别为v10 、v20,求碰撞后速度。
动量守恒:机械能守恒:由(1)(2)式
可以解出2 特例:质量相等的两物体发生弹性正碰小结1.利用动量守恒的解题步骤:
(1).确定研究对象(系统) (2).判断是否守恒 (3).确定正方向 (4).分析初、末态的总动量 (5)..列出方程求解 2.动量守恒定律的优点:
(1)可用于物体在变力作用下的运动情况
(2)只需考虑初、末状态,不需考虑细节
(3)应用范围更广泛3. 碰撞中动量守恒与系统的能量(动能)守恒的运用。作业:
课本12页第1题,第4题
同课章节目录
