专题11 浮力(一)(含答案+解析)-【中考真题汇编】2025年中考物理真题分类汇编(全国通用)
文档属性
| 名称 | 专题11 浮力(一)(含答案+解析)-【中考真题汇编】2025年中考物理真题分类汇编(全国通用) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-12 10:38:14 | ||
图片预览




文档简介
专题11 浮力(一)
一、选择题
1.(2025·武威) 小栋了解到伽利略温度计的测温原理后,想自己动手设计一个粗略测温的装置,他的设计思路如下:在密闭的玻璃容器中装上一种密度会随温度升高而减小的特殊液体,液体中有5个体积相等、密度不同且标有温度示数的小球,小球不吸收液体且热胀冷缩可以忽略不计,当有小球悬浮时,悬浮小球上标有的温度值就是当前环境的温度。如图所示,是这个测温装置的示意图。其中小球3上所标温度值为25℃,相邻标号的小球上所标的温度值间隔为2℃,则下列说法正确的是( )
A.27℃时,小球2处于漂浮状态
B.小球2在27℃时所受的浮力小于25℃时所受的浮力
C.若有3个小球漂浮,2个小球沉底,则环境温度在23℃至25℃之间
D.若要增大该装置能测得的最高温度,可增加一个与小球5体积相等但质量更大的小球
2.(2025·凉山) 《天工开物》中记录了我国古代劳动者煮海水制盐的方法,对用于制盐的海水密度有严格要求。关于海水等级的测评,《熬波图咏》中谈到,可以用莲子制备成四颗不同标准的“浮子”来测定海水等级。测定时,浮起的“浮子”数量越多,待测海水的等级越高(一等海水密度最大等级最高、二、三、四、五等依次次之)。若将以上四颗“浮子”放入盛有待测海水的竹管内,“浮子”的沉浮情况如图所示,下列选项正确的是( )
A.竹管内待测的海水为一等海水
B.①号“浮子”的重力比其它三颗“浮子”大
C.①号“浮子”的密度比其它三颗“浮子”大
D.若竹管内改盛四等海水,①号“浮子”所受浮力不变
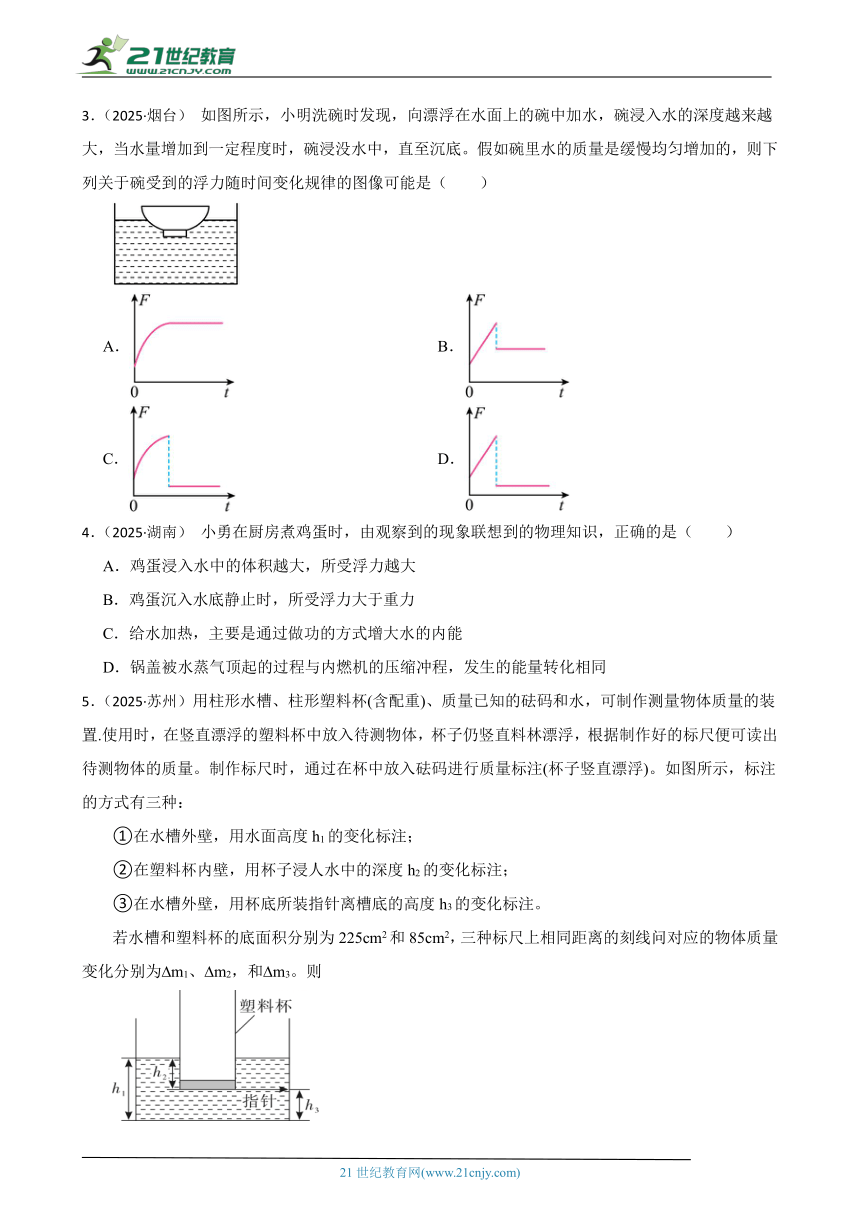
3.(2025·烟台) 如图所示,小明洗碗时发现,向漂浮在水面上的碗中加水,碗浸入水的深度越来越大,当水量增加到一定程度时,碗浸没水中,直至沉底。假如碗里水的质量是缓慢均匀增加的,则下列关于碗受到的浮力随时间变化规律的图像可能是( )
A. B.
C. D.
4.(2025·湖南) 小勇在厨房煮鸡蛋时,由观察到的现象联想到的物理知识,正确的是( )
A.鸡蛋浸入水中的体积越大,所受浮力越大
B.鸡蛋沉入水底静止时,所受浮力大于重力
C.给水加热,主要是通过做功的方式增大水的内能
D.锅盖被水蒸气顶起的过程与内燃机的压缩冲程,发生的能量转化相同
5.(2025·苏州)用柱形水槽、柱形塑料杯(含配重)、质量已知的砝码和水,可制作测量物体质量的装置.使用时,在竖直漂浮的塑料杯中放入待测物体,杯子仍竖直料林漂浮,根据制作好的标尺便可读出待测物体的质量。制作标尺时,通过在杯中放入砝码进行质量标注(杯子竖直漂浮)。如图所示,标注的方式有三种:
①在水槽外壁,用水面高度h1的变化标注;
②在塑料杯内壁,用杯子浸人水中的深度h2的变化标注;
③在水槽外壁,用杯底所装指针离槽底的高度h3的变化标注。
若水槽和塑料杯的底面积分别为225cm2和85cm2,三种标尺上相同距离的刻线问对应的物体质量变化分别为 m1、 m2,和 m3。则
A. m1> m2> m3 B. m2> m1=m3
C. m1> m3= m2 D. m3> m1> m3
6.(2025·眉山) 水平桌面上的甲、乙两个相同圆柱形容器,内装不同液体。将两个相同小球分别放入甲、乙两容器中,小球静止时如图所示。若两容器底部所受液体压强相等,则下列判断正确的是( )
A.两容器中液体密度相等
B.两容器所装液体的质量相等
C.甲容器对桌面的压强小于乙容器对桌面的压强
D.甲容器中小球所受浮力大于乙容器中小球所受浮力
7.(2025·遂宁) 2024年12月,我国春节申遗成功。欢度春节期间,人们有“放鞭炮”“舞龙狮”“逛庙会”“吃汤圆”等习俗。关于春节习俗中的物理现象,下列描述错误的是( )
A.鞭炮爆炸与内燃机做功冲程的能量转化方式相同
B.舞龙狮时力改变了物体的运动状态
C.庙会上各种小吃香气四溢是一种扩散现象
D.汤圆漂浮在水面上时受到的浮力大于重力
8.(2025·北京市)某小组设计了水箱自动控制进水装置,如图所示。水箱内的圆柱形金属控制棒用不可伸长的细线悬挂在力传感器下面,并始终浸在水中,通过它对力传感器拉力的大小触发开关,控制水泵自动进水。用水时,水箱内水位降低,当到达最低水位时,力传感器所受拉力等于F1,触发开关,水泵开始持续向水箱注水;当水位到达最高水位时,力传感器所受拉力等于F2,再次触发开关,水泵停止向水箱注水。若进水过程中同时用水,相同时间内进水量大于出水量。已知控制棒质量为m,水的密度为ρ水。下列说法正确的是( )
A.控制棒受到的浮力最大时,排开水的体积为
B.控制棒受到的浮力的变化量最大为mg-F2
C.力传感器受到的拉力大小在F1与F2之间时,说明水箱正在进水
D.缩短悬挂控制棒的细线,可使水箱中的最高和最低水位均升高
9.(2025·山东) 小华在相同气球内装上不同配重做了两个“小鱼”。“小鱼”甲的质量大于“小鱼”乙的质量。注射器可以通过连接“小鱼”的软管对“小鱼”进行抽气和充气,从而改变“小鱼”的体积。初始时,两“小鱼”在水中处于静止状态,如图所示。忽略空气重力及软管对“小鱼”的作用力。“小鱼”所受浮力分别用F甲、F乙表示。下列说法正确的是( )
A.对甲充气,甲上浮,再次静止时F甲小于F乙
B.对甲抽气,甲下沉,再次静止时F甲一定小于F乙
C.对乙充气,乙再次静止时所受浮力比初始时的浮力小
D.对乙抽气,乙再次静止时所受浮力可能等于初始时的浮力
10.(2025·陕西)研学活动中,小明捡到一块石头。他用电子秤和玻璃杯测量其密度,测量过程如图所示。下列判断不正确的是(不计绳子的质量和体积,水的密度为1g/cm3,g取10N/kg) ( )
A.根据本次实验数据,可得出石头密度最准确的测量值为3.125g/cm3
B.从水中取出石头时,带出了1g的水
C.从水中取出石头时,带出的水不会影响密度的测量值
D.石头沉在水底时,杯底对石头的支持力为0.24N
二、填空题
11.(2025·凉山) 2025年5月10日,代号“鲲龙”的水陆两栖飞机AG600,批产首架机总装下线。这是我国自主研制的全球最大的水陆两栖特种用途飞机。“鲲龙”飞行时机翼上方受到空气的压力 下方受到空气的压力(选填“大于”“小于”或“等于”)。如图甲所示,匀速飞行的“鲲龙”在投水灭火时,其动能会 (选填“变大”“变小”或“不变”)。“鲲龙”执行海上救援任务时,可一次性救援50名遇险人员。在海上救援时,“鲲龙”静止在水面,如图乙所示,若此时遇险人员被救上“鲲龙”,它受到的浮力 (选填“变大”“变小”或“不变”)。
12.(2025·遂宁) 2024年12月,我国自主研制建造的076型两栖攻击舰首舰——“中国人民解放军海军四川舰”正式下水,该舰满载排水量(排开水的质量)4万余吨。若以满载排水量4万吨来计算,该舰满载时所受浮力大小为 N。不考虑燃料质量变化,该舰由海水密度较小的近海驶向海水密度较大的远海区域时,排开海水的体积将 (选填“变大”、“变小”或“不变”)。(g取10N/kg)
13.(2025·黑龙江) 小宁同学把一个质量为50g的木块放在水中,木块漂浮时有的体积露出水面,则这个木块受到的浮力是 N,它的密度是 g/cm3。
14.(2025·齐齐哈尔) 某材料不吸收液体,在酒精或盐水中均不溶解,且不与酒精或盐水发生化学反应,用该材料制成重的实心球。若将球投入足够多的酒精中,当球静止时,受到的浮力大小是 ;若将球投入足够多的盐水中,当球静止时,受到的浮力大小是 N。(已知,,)
15.(2025·陕西)小明想测量一个长方体物块的密度,他用细线提着物块缓慢放入盛有水的杯中,如图-1所示,压力传感器的示数随物块浸入深度的变化关系如图-2所示。整个过程中物块受到浮力的变化情况是 ,已知物块的质量为2.4,则物块的密度为 。剪断细线、当物块静止后压力传感器的示数为 N。(水的密度为,g取10)
三、实验探究题
16.(2025·扬州)小明发现冰块在不同饮料中熔化快慢不同,决定探究影响冰块熔化快慢的因素.
(1)相同的0℃的冰块在某液体中熔化得快,说明相同时间内,冰块在该液体中吸收的热量 (选填“多”或“少”).
(2)若将两个相同的0℃的冰块分别放入水和浓盐水中,所受浮力分别为F 、F盐水,与液体接触面积分别为S水、S盐水,则 F水 F盐水,S水 S块水.
(3)为探究冰块熔化快慢与接触面积的关系,下列两个方案,应选用方案 .
方案一:如图1、2,取两个相同的0℃的冰块,一块直接放入水中,另一块竖切成4 小块放入相同的水中,记录冰块完全熔化的时间分别为t1、t2.
方案二:如图3.4,在装满相同温度的水和浓盐水的玻璃杯中,分别放入相同的0℃的冰块,盖上杯盖使冰块保持浸没,记录冰块完全熔化的时间分别为t3、t4.
(4)①采用方案一进行实验,发现 ,得出的结论是 .
②采用方案二进行实验,发现 ,得出的结论是 .
(5)在用方案二进行实验前,小明根据“向积雪的公路上撒盐,盐能尽快地融雪”,预测冰块在浓盐水中熔化得更快.他的推理是否正确 ,请说明理由: .
17.(2025·江西)亲爱的同学,请你运用所学的物理知识解答下列问题。
(1)如图甲所示,某同学遵照“红灯停,绿灯行,斑马线上安全行”的交通安全知识行走在上学路上,步长约0.6m,直行通过马路共走了32步,并用秒表先后记录了开始和结束时的时间(如图乙和丙所示)。则马路的宽度约为 m,该同学通过马路的时间为 s,速度约为 m/s。
(2)如图所示,重力为1.5N的物体静止在水中。弹簧测力计的示数为 N,物体所受浮力的大小为 N
(3)某同学在“探究水在沸腾前后温度变化的特点”实验中,放置温度计时(如图所示),其操作错误是将温度计的玻璃泡接触了 :纠正错误后继续实验,得出水沸腾时的特点:水持续吸热,温度保持 .
18.(2025·新疆) 小华在实验室里测量土豆的密度,实验操作如下:
(1)用 (选填“天平”或“测力计”)测出洗净的土豆样品的质量为220g;
(2)用细线系住土豆样品,缓慢放入装有400mL水的量筒内,土豆排开的水的体积越大,土豆受到的浮力越 (选填“大”或“小”);土豆最终在量筒内静止时如图所示,则土豆样品的密度为 g/cm3;
(3)小华通过查阅资料知道,土豆密度越大,淀粉含量越高,土豆品质越好。可以采取如下方法来评定土豆的品质:先用弹簧测力计测量出土豆样品的重力G;然后把土豆样品浸没在水中(未接触容器底)静止时,读出测力计的示数F,则的值越 (选填“大”或“小”),土豆品质越好。
19.(2025·泸州)实践出真知。“九章”社团的同学们利用所学知识进行跨学科实践——自制密度计。
(1)他们用铁钉插入粗细均匀、横截面积为0.2cm2的吸管并密封,制作了第一代密度计。使用铁钉的目的是使吸管重心降低、在液体中竖直 ,测试时将其放入密度为 1.0g/cm3的清水中,测得它的吃水深度为10.5cm;取出再放入盐水中,测得它的吃水深度为10.0cm, 则盐水的密度为 g/cm3,发现两次吃水深度相差很小,同学们猜想可能是吸管横截面积太小的缘故:
(2)于是, 他们用横截面积较大、粗细均匀的柱形瓶做了第二代密度计,测试时发现它在清水和上述盐水中的吃水深度差与第一代密度计几乎一样,老师提出:根据密度计在两种液体中受到液体对它的力相等,可推出这种粗细均匀的密度计在清水和盐水中的吃水深度的比值关系是别: 用、表示);
(3)同学们围绕怎样增大吃水深度差这一问题,结合前两次的制作经验,将设计思路和数据输入某AI软件,设计了如图所示的第三代密度计,若第三代密度计在清水中的吃水深度仍为10.5cm, 则它在上述盐水中吃水深度为 cm. 若它在某种液体中的吃水深度为 15.0cm, 则这种液体的密度为 g/cm3.(以上结果保留两位小数)
20.(2025·齐齐哈尔) 小明在得出浸在液体中的物体受到的浮力大小跟物体本身因素无关的结论后,进一步探究“浮力的大小跟哪些因素有关”;
表一
实验次序 液体种类 物体下表面浸入水中的深度/cm 弹簧测力计的示数/N
1 水 0 2.7
2 2 2.2
3 4 1.7
4 6 1.7
… … …
(1)如图甲所示,小明将装有适量水的烧杯放在盘中,用手把空的饮料罐沿竖直方向逐渐按入水中。此过程中,手感受到饮料罐受到的浮力逐渐增大。小明通过分析现象提出猜想,浮力大小可能跟物体浸入液体的深度或物体浸在液体中的 有关。通过其他生活经验,小明还猜想浮力的大小可能跟液体密度有关;
(2)小明用图乙的实验装置进行实验。将盛有适量水的容器放置在桌面上,正确使用弹簧测力计,将一个长方体铝块(高为)用细线悬挂在弹簧测力计下。使铝块沿竖直方向逐渐下降,缓慢浸入水中。实验过程中,保持弹簧测力计的轴线与铝块的竖直轴线在同一直线上。获取触底前的多组实验数据并记录在表一中;
①分析实验数据可知,铝块受到的重力是 N,第2组实验中铝块受到的浮力是 N;
②分析第1、3、4三组实验数据可知,浮力大小跟物体浸入液体的深度 (选填“有关”或“无关”);
③分析第1、2、3三组实验数据可得出初步结论: ;
(3)小明根据实验的初步结论,设计了用图丙所示装置测量某液体密度的方案:
①将3个空的相同厚底薄壁圆柱形玻璃容器(高为)放入足够深的水槽中,待稳定后,容器A、B、C都保持竖直静止,测得容器A、B、C浸入水中的深度均为;
②向容器B、C中分别缓慢装入 (选填“质量”或“体积”)相等的某液体和水。待稳定后,容器A、B、C保持竖直静止,且未触底。测量容器B、C浸入水中的深度,将容器A、B、C浸入水中的深度记录在表二中;
③分析表二中的数据,通过计算可知,液体的密度 。
表二
容器 A B C
容器浸入水中的深度/cm 6 12 11
21.(2025·长沙) 如图是探究浮力的大小是否跟物体浸没的深度有关的实验过程。
(1)实验时,应先将弹簧测力计在 方向调零;
(2)乙图中物体所受浮力为 N;
(3)请你分析实验数据,判断物体所受浮力的大小是否跟物体浸没的深度有关,并说明理由。
22.(2025·吉林) 学校科技小组进行了“测量小石块密度”的实验。
(1)用天平测小石块的质量,当天平平衡时,右盘中的砝码和标尺上游码的位置如图甲所示,小石块的质量为 g,用量筒和水测得小石块的体积为20cm3,则小石块的密度为 kg/m3。
(2)利用浮力知识,科技小组的同学又用另一种方法测出了小石块的密度。步骤一:如图乙所示,将长方体物块放入柱形盛水容器中,物块漂浮,测出物块浸入水中的长度。
步骤二:如图丙所示,将小石块放在物块上,测得物块浸入水中的长度与图乙相比增加了h1,此时物块受到的浮力与图乙相比
步骤三:如图丁所示,将小石块用细线(细线体积和质量均忽略不计)系在物块下,测得物块浸入水中的长度与图乙相比增加了h2,图丁中水对容器底部的压强 图丙中水对容器底部的压强(填“大于”、“等于”或“小于”)。
根据以上信息可得,小石块密度的表达式为ρ石= (用ρ水、h1、h2表示)。
23.(2025·北京市)某同学利用一个圆柱形容器、一个梨、记号笔、刻度尺和适量的水测量酱油的密度,测量过程如图所示,图中h1、h2、h3、h4分别是梨放入水、酱油前后液面到容器底的距离。已知水的密度为ρ水,则待测酱油的密度ρ酱油= 。(用已知量和测量量表示)
四、计算题
24.(2025·凉山) 如图甲所示,在上、下截面均为圆形的锥形瓶内,装有一定量的水。已知锥形瓶上部分是横截面积为的圆筒,且粗细均匀,底面积为。现将质量为32g,边长为2cm的正方体合金块放入锥形瓶内,水未溢出,如图乙。求:
(1)合金块的重力大小;
(2)合金块放入锥形瓶内稳定后所受浮力大小;
(3)如图乙,稳定后,合金块对锥形瓶底的压强;
(4)合金块放入锥形瓶前后,水对锥形瓶底的压力变化量。
25.(2025·广安)某同学看了我国航空母舰发展简介后对力学产生了浓厚的兴趣。他用底面积为的长方体容器(厚度不计)装一定量的水,将一个重为4N,边长为10cm的正方体A放入容器中处于漂浮状态。如图所示,此时水的深度为18cm。(,g取10N/kg)求:
(1)容器底部受到水的压强;
(2)A漂浮时浸入水中的深度;
(3)若将与A形状体积完全相同的物体B平放在A的正上方,A、B一起向下运动,当静止时一起处于悬浮状态。求A、B一起开始运动到B刚好浸没时,B的重力做的功。(容器足够高,水不溢出,A、B不吸水)
26.(2025·新疆) 如图甲所示,A、B两个薄壁圆柱形容器下半部用细管(体积不计)水平连通后放在水平地面上,将18kg水经A容器缓慢的注入整个装置的过程中,水对A容器底部的压强p与注入的水的质量m的关系如图乙所示。将一个内部有许多小气泡的冰球投入到A容器中(水未溢出),水面刚稳定时冰球露出水面的体积,此时B容器中水的深度增加了。已知冰的密度为,求:
(1)质量为18kg的水的重力;
(2)当往整个装置中注入水的质量为5kg时,水对B容器底部的压强;
(3)冰球放入A容器中水面刚稳定时,冰球内部气泡的总体积V气。
27.(2025·河北)小明利用双休日清理家中的鱼缸。长方体空鱼缸的重力G为64N,小明将鱼缸和假山石清洗干净,放到水平桌面上,鱼缸与桌面接触面积 S为0.16cm2, 向鱼缸中注入 h为0.2m深的水,然后将假山石(不吸水)浸没在水中,如图所示。已知假山石的体积 V石为,水的密度 , g取10N/ kg。
求:
(1)空鱼缸对水平桌面的压强。
(2)放入假山石前,水对鱼缸底的压强。
(3)浸没在水中的假山石受到的浮力。
28.(2025·乐山) 如图所示,某同学用一个上端开口的圆柱形厚底空塑料瓶和装有水的圆柱形水槽制作了一个浮力秤,用于测量质量。空塑料瓶质量为120g,塑料瓶底面积为,水槽底面积为,瓶身能够浸入水中的最大长度为18cm,使用过程中水不溢出,塑料瓶始终漂浮且瓶身保持竖直。已知水的密度为,g取10N/kg,不考虑塑料瓶侧壁的厚度。求:
(1)空载时塑料瓶受到的浮力;
(2)浮力秤的最大称量值;
(3)浮力秤空载时和最大称量时水槽内水面的高度差。
29.(2025·泸州)科创小组的同学设计了如图甲所示的力学综合实验装置,力传感器A上确固定在水平杆上,下端通过竖直轻杆与正方体E相连,水平升降台上放有溢水杯c和力传感器B,小桶D放在力感器B上,溢水杯C中的水面刚好与溢水口齐平,水平升降台匀速上升,当t=0时,正方体E刚好接触水面,之后排开的水全部流入小桶D中,力传感器B的示数FB随时间t变化的关系如图乙所示。已知g=10N/kg.ρ水=1.0x103kg/m3.
(1)当力传感器B的示数FB=5N时, 求正方体E受到的浮力:
(2)求升降台匀速上升的速度:
(3)当t=10s时,力传感器A的示数FA=2N,求正方体E的密度。
30.(2025·宜宾) 某锻造厂利用卷扬机将一圆柱形工件(污垢的质量和体积忽略不计)吊入柱形清洗池中清洗,如图所示。已知工件的质量为90kg,高度为50cm,清洗池底面积为2000,深度为80cm;未放入工件时,清洗液的深度为60cm,密度,。求:
(1)工件的重力;
(2)工件一半浸入清洗液时,清洗液对工件底部的压强;
(3)工件完全浸入清洗液,平衡时绳对工件的拉力为700N,工件的底面积是多少;
(4)若工件以1.5cm/s的速度浸入清洗液,则工件从接触液面到刚好完全浸入所用的时间为多少,写出此过程清洗液对清洗池底部的压强随时间变化的关系式。
31.(2025·广西) 某同学探究不同密度的物块在液体中的特点,如图所示,现有质地均匀,不吸水的正方体物块A和B,其质量分别为和、边长分别为和,以及内部边长为的正方体玻璃容器。已知水的密度。取。求:
(1)将物块A放置于玻璃容器底部中央,物块A对容器底部的压强;
(2)往容器内缓慢注水,物块A不上浮,当水深为时,水对容器底部的压强和注入水的体积;
(3)接着把物块B放在物块A的正上方。再将质量为的水缓慢注入容器。在此过程中,水对物块B所做的功。
32.(2025·德阳) 如图甲所示,“国之重器”起重船起吊重物时,需通过抽水机将一侧水舱里的水抽向另一侧水舱来保持起重船平衡。如图乙所示,小兰设计了一种采用力传感器感知抽水量的长方体水舱模型,水舱中装有的水,其底面积。A是固定在顶端的力传感器,能够显示A对B的压力或拉力的大小;B是质量和体积均可忽略的细直硬杆,不考虑B的形变,B的上端与力传感器A连接,下端与物体C连接;物体C是质量、底面积的圆柱体。用抽水机将水抽出的过程中,力传感器示数的大小随抽出水的体积变化的图像如图丙所示。当物体C的下端刚好露出水面,此时已抽出水的体积。已知。求:
(1)物体C的重力;
(2)物体C完全浸没时排开水的体积;
(3)当力传感器示数为时,水对水舱模型底部的压强。
33.(2025·眉山) “雪龙”号是我国最大的极地考察船,排水量约,吃水深度可达,动力系统中,主机功率。取,,求:
(1)“雪龙”号满载时受到的浮力;
(2)水面下5m深处船壁受到海水的压强;
(3)如图所示,执行科考任务的“雪龙”号在海面破冰前行,假如船以的速度做匀速直线运动,主机能提供多大的动力。
34.(2025·遂宁) 小聪为学校的鱼池设计自动补水装置,实现鱼池中水位处在1.4m到1.6m之间,适宜鱼儿生长。他设计的装置如图甲,L为一根上端固定的轻质弹簧(可视为导线),弹簧拉力大小与伸长量的关系如图乙。塑料圆柱形密闭浮筒A的底面积,高0.2m,质量0.3kg。电源电压恒为6V,,为一根足够长的电阻丝,其阻值与接入电路中的长度成正比,滑片P可随浮筒A竖直上下移动。电压传感器(对电路无影响,未画出)监测两端的电压,当两端电压达到4V,传感器控制注水阀门打开;当两端电压低于2V时,传感器控制注水阀门关闭。通过调试:当水位降到最低1.4m时,浮筒A底部刚好接触水面,滑片P位于的某一位置,注水阀门打开:当水位上升到最高1.6m时,注水阀门关闭。(,g取10N/kg)求:
(1)浮筒A的重力;
(2)水位最低1.4m时的阻值;
(3)到达最高水位1.6m时,浮筒A底部受到水的压强,以及接入电路中的总长度;
(4)小聪还想在电路中串联一个电流表,将其改装为一个水位计,请帮他找出水位高度在1.4m到1.6m时,电路中电流I(单位:A)与水位高度H(单位:m)的函数关系式。
35.(2025·威海) 如图甲所示,某航海器由钢板焊接的两个空心三棱柱组成。侧面为ABCDE;在△ABC中,AB=8m,AC=BC,;在中,底边DE的高为0.9m;两个三棱柱棱的长度均为10m,下方三棱柱体积为6m3,航海器总重(,g取10N/kg,三棱柱体积=三角形面积×棱的长度)
(1)当航海器漂浮在水面上,求排开水的体积。
(2)航海器误入浅水区搁浅,下方三棱柱一部分陷入泥沙,如图乙所示。
为将航海器浮起来,采取了以下措施:卸掉重2×105N的设备,等待涨潮之后清理下面的泥沙。搁浅位置24小时内,航海器底部到水面的距离H随时间变化情况如图丙所示。假设航海器整体始终保持水平,请通过计算判断航海器是否能浮起来?
36.(2025·深圳)如图是深圳号在海上航行,田田同学乘坐了这艘船出海游玩。田田发现这艘船最大吃水高度是9米,最大排水量是70000吨,船上一汽车用钢打造,钢的体积0.1立方米。(已知:钢的密度是 海水密度
求
(1)钢的质量,
(2)求轮船所受的浮力,
(3)船底面积是 ,求轮船底部受到的压力。
37.(2025·黑龙江) 如图,这是一款国产水陆两栖汽车航行技术测试的现场。这辆汽车在水中的最大速度约为8.3km/h。良好的密封技术和防锈处理,使车体的吃水深度达到1.05m,满载时排开水的质量达到4×103kg。求:
(1)如果汽车用7.2km/h速度在水中航行30min,它航行的距离;
(2)当汽车在水中航行时,若车的底部距水面0.8m,车底受到水的压强;
(3)汽车在水中满载航行时受到的浮力。
38.(2025·广东)题图所示是我国自主设计建造的“极地”号破冰调查船,某次任务中,该船的总质量为4.12x106kg.已知g=10N/kg,ρ海水=1.03×103kg/m3,q燃油=4.3×107J/kg.求该船:
(1)受到的总重力:
(2)静止时排开海水的体积:
(3)发动机完全燃烧100kg燃油放出的热量.
39.(2025·绥化) 如图所示,水平桌面上有一个圆柱形薄壁容器。容器内竖立一个圆柱形杯子(材料质地均匀),高为0.09m,底面积为。现只向容器内注水,当容器内水的深度为0.06m时,杯子对容器底部的压力刚好为零;接下来同时向容器内和杯中注水,当杯口与容器内的水面相平时,杯中水的体积是杯子容积的一半,且杯子对容器底部的压力也刚好为零。(整个过程中,杯底与容器底部始终接触但不紧密)求:
(1)只向容器内注水,当水的深度为0.06m时,水对容器底部的压强;
(2)空杯子的质量;
(3)该杯子材料的密度;
(4)继续向杯子中注水,直至注满,此时杯子对容器底部的压强是多少?
五、综合题
40.(2025·云南) 2024年11月17日,我国建造的全球最先进的大洋钻探船“梦想”号正式入列,如图甲所示。它具备11000米超深水钻探能力,有望实现“打穿地壳,进入地球深部”的科学梦想。钻探船上高耸的井架控制钻杆作业,使钻头深入海底钻取岩心。
(1)“梦想”号钻探船上建有高耸的井架,出海执行任务时,要从大桥下通过。只要 (选填“空载”或“满载”)时能通过大桥,就能始终确保安全通行。
(2)求在水深5000m处海水对钻头的压强。取)
(3)科创小组估测井架质量为,井架与甲板接触面积为,求井架对甲板的压强。
(4)为了研究“梦想”号钻探船从桥下安全通行的高度问题,科创小组用两块相同的等腰梯形板材和三块长边均为的矩形板材,制作了如图乙所示的“启航”号实验船,板材不吸水且厚度不计。船底短边,船身高度,,船头竖立有旗杆。将船放入平静的湖水中进行实验,当装载货物时,吃水深度为。若桥离水面的高度,要实验船始终能安全通过此桥,求旗杆的最大高度。(货物高度始终低于旗杆顶部,)
41.(2025·贵州) 某次学校物理社团活动主题是“制作浮力秤”。经思考,小明决定用薄壁硬质饮料瓶、水槽、水、细线及几个质量不同的重物进行制作。他设想,让饮料瓶漂浮于水面,在瓶身上标记出相应的质量刻度线,把待测物体放入瓶中,待水面静止时,根据水面所在刻度线的位置,便可读出待测物体质量。小明进行如下制作:
【任务一】制作秤体
小明切掉饮料瓶底部,用细线将瓶盖与其中一个重物连接,旋紧瓶盖,将瓶体开口向上倒置于水槽中,待其静止后,若瓶体呈竖直状态,且与重物整体漂浮,则秤体制作完成,如图甲所示。此时瓶体便可作为秤盘盛放待测物体。
(1)此时秤体所受浮力大小 其重力大小。
(2)【任务二】标注刻度
小明认为当秤体漂浮,且水面位于瓶体的圆柱状部分时才便于标记刻度。他发现图甲中秤体在水中的位置尚未满足标记刻度的条件。
为满足条件,小明用准备的器材进行调整,请你给他提出调整建议 。
调整完成后,小明先将饮料瓶身与水面齐平处标记为0cm,此处即为质量标度的零刻度线;将饮料瓶取出,再将刻度尺对应的长度刻度值标记在瓶身上;测量出饮料瓶圆柱状部分的横截面积为50cm2,再放入水中,如图乙所示。
(3)接下来,只需将瓶身上所标注的长度刻度值转换为相应的质量标度,便可完成浮力秤的制作。请你计算瓶身上刻度1cm处所对应的质量标度为多少克?()
小明按照此方法计算并标注了浮力秤各刻度值对应的质量标度。
(4)【任务三】拓展分析
小羽参照小明的方法,用一个横截面为圆形,切口处圆的面积也为50cm2,但上下粗细不同的饮料瓶来制作浮力秤。她正确标记了零刻度线的位置,用刻度尺紧贴瓶身,在瓶身上标注了均匀的刻度,如图丙所示;接着她依照小明浮力秤的刻度值,在相同的刻度处标注了相同的质量标度(图中未画出)。
请判断小羽制作的浮力秤所称出的物体质量比真实值偏大还是偏小?说明理由。
42.(2025·天津市)在跨学科实践活动中,同学们制作了如图所示的“浮力秤”,用来称量物体的质量。圆柱形薄壁外筒足够高且内装足量的水,带有秤盘的圆柱形浮体竖直漂浮在水中,浮体浸入水中的深度为 。已知浮体横截面积为S0,外筒横截面积为3S0,水的密度为ρ0。
(1)浮体和秤盘的总质量为 ;
(2)秤盘中未放物体,在水面位于浮体的位置标为“0”刻度线;秤盘中放质量为m1的砝码,在水面位于浮体的位置标为“m1”刻度线。请推导出这两条刻度线间的距离△h的表达式 ;
(3)为了测算该“浮力秤”的最大测量值,先把带有秤盘的浮体直立在外筒底部(图),再向外筒内缓慢注水,外筒底部受到水的压强与注入水质量的关系如图所示。当外筒底部受到水的压强至少为p1时,此“浮力秤”能够达到最大测量值,该最大测量值为 。
答案解析部分
1.C
AB、图中,悬浮时,物体的密度等于液体的密度,小球3此时悬浮,对应的温度为25℃,小球2漂浮,当温度继续升高为27℃时,液体密度减小,小球2将下沉,直至悬浮,小球2漂浮和悬浮时,受到的浮力等于小球2的重力,浮力不变,AB错误;
C、图中,小球4、5沉底,小球3悬浮,此时的温度在23℃~25℃间,C正确;
D、若增大所测量的最高温度,则液体密度更小,悬浮的小球的密度更小,需要增加体积相同,比小球1的密度更小的球,D错误。
故选C。
悬浮和漂浮时,物体受到的浮力等于物体的重力;悬浮物体的密度等于液体的密度;液体在温度升高时,密度减小;温度升高时,液体密度减小,悬浮的物体密度减小。
2.C
ABC、根据浮沉条件知,1号沉底,其密度大于液体的密度,而2、3、4漂浮,密度都小于液体的密度,根据漂浮时浮力等于重力,F浮=ρ水gV排=G=ρgV;
漂浮时如果物体的浸入的体积占总体积的比例越大,物体的密度就越接近液体的密度,即密度越大,ρ2>ρ3>ρ4;密度关系ρ1>ρ2>ρ3>ρ4;
根据G=mg=ρVg,已知密度关系,但不知道体积关系,故无法比较重力大小,
图中2号接近悬浮,密度在1、2之间,所以该海水为二等海水;故AB错误,C正确;
D、图中1号沉底,改盛四等海水,液体的密度更小,因而还是沉底,故排开液体的体积不变,但液体密度变小,根据阿基米德原理知,浮力减小,故D错误。
故答案为:C。
由图乙可知4个浮子在海水中的浮沉情况,根据浮沉分析其密度与液体密度关系解答;根据G=mg=ρVg比较重力,根据浮子的浮沉确定密度等级;根据阿基米德原理分析①号“浮子”所受浮力。
3.D
向漂浮在水面上的碗中加水,碗浸入水的深度越来越大,排开液体的体积增大,由F浮=ρ水gV排可得,所受浮力变大,
碗浸没水中,排开水的体积变小,由F浮=ρ水gV排可得,所受浮力变小,由于 碗里水的质量是缓慢均匀增加的,应该是线性关系,所以浮力先增大,后减小,最后不变,故只有D图符合题意。
故选D。
分析出排开液体的体积的变化,根据阿基米德原理判断出沉底前的浮力变化;碗沉底后排开水的体积不变,根据阿基米德原理判断出受到浮力的变化。
4.A
A.根据阿基米德原理F浮=ρ液gV排,液体密度液不变,鸡蛋浸入水中的体积排越大,所受浮力越大,故A正确;
B.鸡蛋沉入水底静止时,处于平衡状态,但此时浮力小于重力,所以鸡蛋才会下沉到水底,故B错误;
C.给水加热,主要是通过热传递的方式增大水的内能,而不是做功,故C错误;
D.锅盖被水蒸气顶起的过程是内能转化为机械能,与内燃机的做功冲程能量转化相同;而内燃机的压缩冲程是机械能转化为内能,二者能量转化不同,故D错误。
故选A。
A.根据阿基米德原理F浮=ρ液gV排分析判断;
B.根据浮沉条件分析判断;
C.改变物体内能的方式有两种:做功和热传递,热传递过程是能量的转移过程,做功过程是能量的转化过程。
D.内燃机的做功冲程能量转化是将内能转化为机械能,内燃机的压缩冲程是机械能转化为内能。
5.C
三种标尺上相同距离的刻线间对应的物体质量变化分别为Δm1、Δm2和Δm3。
假设相同距离的刻线间的距离为Δh;
在水槽外壁,标注刻度,△V排=S容Δh=225cm2×Δh;
根据阿基米德原理和浮力等于重力,ΔG=Δmg=ΔF浮=ρ水gΔV排;
物体的质量变化等于排开水的质量变化,
则△m1=ρ水△V排=ρ水×225cm2×Δh;
②在塑料杯内壁,用杯子浸入水中的深度变化标注;△V排2=S杯Δh=85cm2×Δh;
则△m2=ρ水△V排2=ρ水×85cm2×Δh;
③在水槽外壁,用杯底所装指针离槽底的高度h3的变化标注,当塑料杯下行Δh时,液面会升高,且体积变化相等,即S杯Δh=(S容-S杯)L;
;
;
则△m3=ρ水△V排3=ρ水×136.6Δh;
则△m1>△m3>△m2。
故选C。
要比较质量,需要分析重力,根据浮力秤是漂浮,浮力等于重力,因而质量的变化等于重力的变化,也等于浮力的变化,假设刻度的距离,根据所给的底面积计算排开液体的变化,根据阿基米德原理比较液体的重力与质量。
6.B
A、两球相同,甲中漂浮,所以球的密度小于甲中液体密度,乙中悬浮,所以球的密度等于乙液体的密度,所以甲的密度大于乙,故A错误;
B、压强相同,根据F=Ps可知,液体对容器底部的压力相同,压力等于液体的重力,所以液体质量相同,故B正确;
C、甲乙液体的质量相同,小球质量相同,所以总质量相同,对地面的受力面积相同,根据F=Ps可知,压强相同,故C错误;
D、甲乙漂浮和悬浮,重力等于浮力,重力相同,所以浮力相同,故D错误。
综上选B。
1、浮力的本质为上下表面产生的压力差,计算公式为F浮=ρ液gV排,所以物体所受浮力和物体所处的深度无关,与排开水的体积有关,当排开水的体积越小时,浮力越小,排开水的体积越大时,浮力越大
2、阿基米德原理:物体排开水的重力等于物体所受浮力;
3、物体沉浮条件:物体悬浮时的浮力等于重力(排开水的体积等于物体体积),物体的密度等于液体的密度,物体漂浮表明浮力等于重力(排开水的体积小于物体体积),物体的密度小于液体的密度,物体下沉时重力大于浮力(排开水的体积等于物体体积),物体的密度大于液体的密度;
4、压强的计算:公式为P=ρgh,压强和液体的密度、浸没深度有关,且密度越大,压强越大,深度越大,压强越大, 在同种液体的同一深度,液体向各个方向的压强 相同。
7.D
A.鞭炮爆炸内能转化为机械能,与内燃机做功冲程(内能转化为机械能)的能量转化方式相同,故A正确不合题意;
B.力可改变物体的形状,也可改变物体的运动状态,舞龙狮时力改变了物体的运动状态,故B正确不合题意;
C.庙会上各种小吃香气四溢是一种扩散现象,说明分子永不停息地做无规则运动,故C正确不合题意;
D.汤圆漂浮在水面上时受到的浮力等于重力,故D错误符合题意。
故选D。
A.内燃机做功冲程也将内能转化为机械能;
B.力可改变物体的形状,也可改变物体的运动状态;
C.扩散现象说明分子永不停息地做无规则运动;
D.根据物体的漂浮条件分析。
8.D
A.由题意,控制棒受到了重力、浮力和拉力的作用。当水位达到最高水位时,此时力传感器所受的拉力为F2,方向向下,根据力的作用是相互的,控制棒受到的拉力F2',大小等于F2,方向向上。此时控制棒排开水的体积为最大,浮力最大。控制棒的重力、浮力和拉力三个力的关系是:F浮+F2'=G=mg,可知F浮=mg-F2'=mg-F2,由F浮=ρ液gV排得:控制棒此时排开水的体积,故A错误。
B.当水位到达最低水位时,力传感器受到的拉力等于F1,方向向下,根据力的作用是相互的,控制棒受到的拉力F1',大小等于F1,方向向上。此时控制棒排开水的体积为最小,浮力最小。控制棒的重力、浮力和拉力三个力的关系是:F浮min+F1=G=mg,得F浮min=mg-F1,
由以上分析知:最高水位时浮力最大,F浮max=mg-F2,
则浮力的最大变化量ΔF浮max=(mg-F2)-(mg-F1)=F1-F2,故B错误;
C.由题意,最低水位时传感器的拉力为F1,此时控制棒对传感器的拉力最大,水泵启动进水。最高水位时传感器的拉力为F2,此时控制棒对传感器的拉力最小,水泵停止向水箱注水。故注水过程中,拉力逐渐从F1减小到F2。若进水过程中同时用水,相同时间内进水量大于出水量,所以此时水位是上升的,拉力是从F1减小到F2。若水泵停止注水(拉力已达到F2),开始用水,水位下降,则拉力从F2逐渐增大,直到水泵启动(此时拉力为F1)则不管是进水还是出水,拉力确实处于F1和F2之间,故C错误;
D.缩短悬挂控制棒的细线,因F1和F2触发的条件不变,控制棒的重力不变,由F浮=G-F知:则控制棒受到的浮力不变。
根据F浮=ρ液gV排得:,
若初始时细线的长度为L,控制棒的长度为h,水箱底到力传感器的距离为H。控制棒浸入水中的体积为V排,
设浸入深度为d,控制棒的横截面积为S棒,
则V排=S棒d,则,
因mg、F1、ρ水、S棒均不变,所以d不变;
则水位高度y=H-L-h+d,
缩短细线长度L,水位高度y变大,故D正确。
故选D。
物体受到了重力、浮力和拉力的作用,根据平衡力的知识分析这三个力的关系,再结合阿基米德原理进行分析。
9.D
A.图中甲悬浮,浮力等于重力,对甲充气,甲上浮变为漂浮,浮力还等于重力,甲的重力大于乙的重力,乙漂浮,浮力等于重力,再次静止时F甲大于F乙,故A错误;
B.对甲抽气,甲下沉,浮力小于自身重力,若抽出气体后,甲排开水的体积仍大于乙,由阿基米德原理可得,F甲还可以大于F乙,故B错误;
C.对乙充气,本来漂浮的,充气后仍漂浮,两次都是浮力等于重力,故乙再次静止时所受浮力与初始时的浮力相等,故C错误;
D.对乙抽气,如果仍漂浮或恰好悬浮,浮力还等于重力,乙再次静止时所受浮力可能等于初始时的浮力,故D正确。
故选D。
AB.根据漂浮和悬浮时浮力都等于重力分析;
CD.根据浮沉体积结合重力大小关系分析。
10.D
A、据图可知石头的质量为75g,添加水的质量为357g-(408g-75g)=24g,根据密度公式计算添加水的体积为,所以石头的体积为24cm3,根据密度公式计算石头的密度为,故A正确。
B、水和石头的总质量为408g,所以水的质量为408g-75g=333g,有步骤3可知,此时称的示数为332g,所以带出水的质量为333g-332g=1g,故B正确;
C、不计算带出水的质量,最终是将水加到标记处,计算是加水的差值,所以不会导致最终测量结果发生偏差,故C错误;
D、石头的重力G=mg=75×10-2N,石头的体积为24cm3,受到的浮力,所以支持力F=75N-24N=51N,故D错误。
1、浮力的本质为上下表面产生的压力差,计算公式为F浮=ρ液gV排,所以物体所受浮力和物体所处的深度无关,与排开水的体积有关,当排开水的体积越小时,浮力越小,排开水的体积越大时,浮力越大
2、利用水测量待测物体的密度:要保证水的体积和物体的体积相同,根据密度公式计算待测物体的密度。
11.小于;变小;变大
因为机翼上方的空气流速大,压强较小;机翼下方的空气流速小,压强大,这一压强差使飞机获得竖直向上的升力;由于机翼上方的压强小于下方压强,则机翼上方的压力小于飞机下方的压力。匀速飞行的“鲲龙”在投水灭火时,质量变小,速度不变,故动能变小。飞机漂浮在水面上,当遇险人员被救上“鲲龙”后,总重力变大,由物体的漂浮条件可知,飞机所受浮力的变大。
机翼的升力:机翼的上方是弧形,空气流过上方时流速大,压强小;机翼下方是平面,空气的流速小,压强大,这一压强差使飞机获得竖直向上的升力。动能的大小与质量和速度有关;飞机漂浮在水面上,当遇险人员被救上“鲲龙”后,总重力变大,由物体的漂浮条件可知飞机所受浮力的变化。
12.;变小
(1)根据阿基米德原理,浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开液体所受的重力,则该舰满载时所受浮力F浮=G排=m排g=4×107kg×10N/kg=4×108N。
(2)因为该舰在海水中始终处于漂浮状态,所以它受到的浮力始终等于自身重力。当舰由海水密度较小的近海驶向海水密度较大的远海区域时,浮力不变,根据F浮=ρ液gV排可知,ρ液增大,g不变,F浮不变,所以排开海水的体积V排将变小。
(1)由阿基米德原理可知,浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开液体所受的重力。
(2)根据F浮=ρ液gV排分析排开海水的体积变化即可。
13.0.5;0.6
因为木块漂浮在水面,受力平衡,则木块受到的浮力等于木块的重力:
F浮=G木=m木g=50×10-3kg×10N/kg=0.5N,
根据阿基米德原理可知,木块排开水的体积为:
;
木块的体积为:
;
木块的密度为:
。
故答案为:0.5;0.6。
(1)木块漂浮时,受到的浮力等于木块的重力,根据F浮=G=mg求出木块受到的浮力;
(2)根据阿基米德原理可求出木块排开水的体积和木块的体积,根据密度公式求出木块的密度。
14.0.8;1
实心球的质量,
实心球的体积,
若将实心球投入足够多的酒精中,实心球的密度大于酒精密度,故静止时,物体在酒精中沉底,
故此时所受浮力为:F浮'=ρ酒精gV=0.8×103kg/m3×10N/kg×1.0×10-4m3=0.8N;
实心球的密度小于盐水的密度,故在水中静止时,处于漂浮状态,则浮力等于重力,
故静止时物体受到的浮力为:F浮=G=1N。
知道物体的重力和密度,求得物体的质量和体积;
根据物体密度与酒精密度的关系判断出物体在酒精中的浮沉情况,根据阿基米德原理公式算出物体在酒精中的浮力;
将物体的密度和盐水的密度比较,根据物体的浮沉条件确定物体在盐水中的状态和受到的浮力。
15.先变大后不变;;58
据图可知,压力传感器的实数先变大后变小,物体对水的压力和水对物体的浮力属于相互作用力,所以浮力的变化为先变大后不变,据图可知,物体收到的浮力F=54N-34N=20N,物体的体积,密度为,剪短绳子后,采用整体发分析,水、物体、杯子的总重力m=34N+24N=58N,即压力传感器示数为58N。
1、浮力的本质为上下表面产生的压力差,计算公式为F浮=ρ液gV排,所以物体所受浮力和物体所处的深度无关,与排开水的体积有关,当排开水的体积越小时,浮力越小,排开水的体积越大时,浮力越大
2、根据密度公式计算m=ρv分析可知,体积相同是质量和密度成正比。
16.(1)多
(2)=;>
(3)方案一
(4)冰块熔化的快慢和接触面积有关;冰块熔化的快慢和液体密度有关
(5)不正确;向雪地撒盐,降低了雪的熔点,而冰在盐水中熔化,需要吸热,盐水的温度不一定比冰的熔点高,盐水中的冰不一定熔化快
探究影响冰块熔化快慢的因素时,
(1)冰熔化时,需要吸热,相同的冰放在不同液体中,熔化快慢不同,可知,在相同时间内,冰块熔化越快,则吸热越多;
(2)由于冰块相同,则重力相同,当冰在水中和盐水中漂浮时,根据二力平衡,受到的浮力等于冰的重力,则受到的浮力:F水=F盐水,根据F浮=ρ液gV排,盐水的密度比水的密度大,则排开盐水的体积比排开水的体积小,冰与盐水的接触面积比冰与水的接触面积小,则S水>S盐水;
(3)探究熔化快慢和接触面积的关系时,根据控制变量法,只改变接触面积,方案二中,冰块和液体的接触面积不同,但液体也不同,变量不唯一,方案一只改变了冰和水的接触面积,更合理;
(4)①利用方案一进行实验,当t2②方案二中,液体密度不同,熔化时间不同,可知,冰块的熔化快慢可能和液体密度有关;
(5)在雪地撒盐融雪,降低了雪的熔点,而冰在盐水中熔化,需要吸热,盐水的温度不一定比冰的熔点高,盐水中的冰不一定熔化快,可知预测冰块在浓盐水中熔化得更快是不正确的。
(1)固体熔化时,需要吸热,熔化越快,则吸收热量越多;
(2)相同的冰块重力相等,冰块漂浮时,受到的浮力等于重力,则在不同液体中漂浮,浮力相等;根据F浮=ρ液gV排,液体密度密度越大, 排开液体的体积越小,和液体的接触面积越小;
(3)探究冰熔化快慢和接触面积的关系,保持其他条件相同,只改变和液体的接触面积;
(4)在相同环境中,冰和液体的接触面积越大,熔化越快;在不同液体中,熔化快慢不同;
(5)雪地撒盐,可以降低雪的熔点,使雪更容易熔化,盐水的温度不一定高于冰的温度,盐水中的冰不一定熔化快。
17.(1)19.2;16;1.2
(2)1.0;0.5
(3)烧杯底部;不变
(1)根据步长约0.6m,通过马路共32步,计算路程为:s=0.6m×32=19.2m;根据图乙和丙,通过马路的时间为:t=16s,计算通过马路的速度约为:。
(2)图中,物体静止在水中,弹簧测力计的分度值为0.2N,根据指针位置, 拉力为1.0N,结合物体的重力,计算物体所受浮力的大小为:F浮=G-F拉=1.5N-1.0N=0.5N;
(3)探究水沸腾时温度变化规律时,图中,温度计的玻璃泡接触了烧杯底,是错误的:正确实验时,可得:水在沸腾时,持续吸热,温度保持不变。
(1)根据步行的步幅长度和步数,计算路程,结合秒表的指针位置,测量时间,根据,计算速度;
(2)根据测力计指针位置,测量拉力大小,利用物体的重力和浸没时的拉力差,计算浮力;
(3)使用温度将测量温度时,温度计的液泡不能碰到容器底或容器壁;液体沸腾时,吸收热量,温度保持不变。
18.(1)天平
(2)大;1.1
(3)小
(1)天平是测量物体质量的工具。
(2)根据可知,排水体积越大则浮力越大,土豆和水的总体积为600cm3,水的体积为400cm3,所以土豆的体积为200cm3,密度为。
(3)弹簧测力计示数F=G-F浮,土豆的密度越大,则G=ρ物gv排,所以物体的重力越大,,物体浸没在水中,浮力不变,,分析可知,密度越大, 则的值越 小。
1、天平的使用步骤:调零:天平置于水平台上,将游码归零,调节平衡螺母使得指针指向刻度中央,称重:是用镊子夹取砝码,测量时为左物右码,不断调整砝码和游码重量,使得天平重新平衡;测量为左物右码,量筒的使用:确定分度值,视线平行对准液面最低处,进行读数。
2、浮力:浮力产生的原因为上下表面存在压强差,根据阿基米德远离可知浮力的大小等于排开水的重力,浮力的公式F浮=ρ液gV排,应用:通过改变自身重力改变浮力,轮船以及潜水艇。
19.(1)漂浮;1.05
(2)
(3)5.5;0.96
(1)他们用铁钉插入粗细均匀、横截面积为0.2cm2的吸管并密封,制作了第一代密度计。使用铁钉的目的是使密度计重心降低、在液体中竖直漂浮。
测试时将其放入密度为1.0g/cm3的清水中,测得它的吃水深度为10.5cm;取出再放入盐水中,测得它的吃水深度为10.0cm,根据漂浮的特点浮力等于重力,可知两次受到的浮力相同,
由阿基米德原理有:ρ水gl1S=ρ盐gl2S;
即ρ水l1=ρ盐l2;
则盐水的密度为。
(2)因密度计漂浮,密度计在两种液体中受到液体对它的浮力相等,
由阿基米德原理有ρ水gh水S'=ρ盐gh盐S';
可推出这种粗细均匀的密度计在清水和盐水中的吃水深度的比值关系是;
(3)图中密度计下面的圆柱体的体积为V=S1h1=4.0cm2×5.0cm=20cm3=20×10-6m3=2×10-5m3;
故在水中排开水的体积为V水=2×10-5m3+(10.5-5.0)×0.2×10-6m3=2.11×10-5m3------①
设它在上述盐水中吃水深度为l,类似得出在盐水中排开液体的体积为
V盐=2×10-5m3+(l-5.0)×0.2×10-6m3------②
因密度计在两种液体中漂浮,故受到液体对它的 浮力都等于重力,故浮力相等,
由阿基米德原理有ρ水gV水=ρ盐gV盐------③
因 ------④
由①②③④得出:l=5.5cm;
若它在某种液体中的吃水深度为15.0cm,则排开这种液体的体积为
V液=2×10-5m3+(15.0-5.0)×0.2×10-6m3=2.2×10-5m3------⑤
根据阿基米德原理有ρ水gV水=ρ液gV液------⑥
由①⑤得:ρ液=0.96g/cm3
(1)密度计是根据漂浮的特点工作的;根据漂浮的特点浮力等于重力,可知两次受到的浮力相同,由阿基米德原理得出盐水的密度;
(2)因密度计漂浮,由漂浮的特点回答,由阿基米德原理可推出这种粗细均匀的密度计在清水和盐水中的吃水深度的比值关系;
(3)得出第三休密度计下面的圆柱体的体积,从而得出其在水中排开水的体积;设它在上述盐水中吃水深度为l,类似得出在盐水中排开液体的体积;因密度计在两种液体中受到的浮力相等,由阿基米德原理得出它在上述盐水中吃水深度;若它在某种液体中的吃水深度为15.0cm,得出排开这种液体的体积,根据阿基米德原理得出ρ液。
20.(1)体积
(2)2.7;0.5;无关;液体密度一定时,浮力的大小与物体浸在液体中的体积成正比
(3)体积;
(1)根据图中浸入的深度在改变,同时浸入的体积也改变,故浮力大小可能跟物体浸入液体的深度或物体浸在液体中的体积有关。
(2)①根据没有浸入液体时,弹簧测力计的示数等于重力为2.7N;
根据称重法计算浮力知,第2组实验中铝块受到的浮力F浮=G-F=2.7N-2.2N=0.5N;
②分析第1、3、4三组实验数据可知,浸入的深度改变,而拉力不变,说明浮力不变,故浮力大小跟物体浸入液体的深度无关;
③分析第1、2、3三组实验数据可得出初步结论:浸入的体积改变,拉力改变,浮力改变,深度变为2倍,浸入体积变为2倍,浮力分别是F浮=G-F=2.7N-2.2N=0.5N;
F'浮=G-F'=2.7N-1.7N=1N;
浮力变为了2倍,说明是正比关系,故说明液体密度一定时,浮力的大小与物体浸在液体中的体积成正比;
(3)利用浮力测液体密度时,根据浮力等于重力,相当于间接测量了液体的质量,因而控制体积相等;
根据浮沉条件知,增大浮力等于增大的液体的重力,G=F浮;
ρ水gV=1.0×103kg/m3×10N/kg×S×(0.11m-0.06m);
ρ液gV=1.0×103kg/m3×10N/kg×S×(0.12m-0.06m);
解得:ρ液=1.2ρ水=1.2×103kg/m3。
(1)根据图中浸入的体积不同分析;
(2)根据没有浸入液体时,弹簧测力计的示数等于重力,结合称重法计算浮力;
根据控制变量法分析数据得出结论;
(3)利用浮力测液体密度时,根据浮力等于重力,相当于间接测量了液体的质量,故需要控制体积不变;结合左侧数据分析。
21.(1)竖直
(2)0.4
(3)无关,由图丙和图丁可知,物体浸没在不同深度时,弹簧测力计示数不变,由称重法可知浮力不变,说明物体所受浮力的大小跟物体浸没的深度无关
(1)实验前,弹簧测力计要现在竖直方向调零,原因是弹簧测力计要测量重力,重力的方向竖直向下。
(2)根据称重法计算可知,乙图中的浮力F=1.4N-1.0N=0.4N;
(3)由乙丙丁分析可知随着浸没深度逐渐增加,其余因素不变化,弹簧测力计示数不变,所以浮力大小跟深度无关。
1、弹簧测力计:使用前弹簧测力计竖直调零,分度值为0.2N,重力方向竖直向下,据图读数,对钩码的拉力与弹簧测力计的弹簧轴线一致;
2、称重法测量物体浮力:先测出物体的重力,然后将物体浸入水中,弹簧测力计的示数就会减小,减小的示数就是物体受到的浮力;
3、浮力:浮力产生的原因为上下表面存在压强差,根据阿基米德远离可知浮力的大小等于排开水的重力,浮力的公式F浮=ρ液gV排,应用:通过改变自身重力改变浮力,轮船以及潜水艇。
22.(1)54;2.7×103
(2)变大;等于;
(1)据图可知,石头的质量为50g+4g=54g;密度为
(2)物块浸入水中的体积变大,根据浮力公式F=ρgv可知,浮力变大;据图可知,丁丙两图,物块的状态为漂浮,所以浮力等于重力,所以派开水的体积相同,容器的底面积相同,所以上升的高度相同,根据P=ρgh计算可知,丁的压强等于丙;圆柱的底面积为S,物体漂浮,所以重力等于浮力,石头的质量m=;由图丁可知,石头的体积,所以V石=S(h1-h2);所以密度为。
1、测量物体密度试验:原理为ρ=m/v,使用的仪器为天平和量筒;
天平的使用步骤:1、调零:天平置于水平台上,将游码归零,调节平衡螺母使得指针指向刻度中央,
称重:是用镊子夹取砝码,测量时为左物右码,不断调整砝码和游码重量,使得天平重新平衡;测量为左物右码;量筒的使用:确定分度值,视线平行对准液面最低处,进行读数。
2、阿基米德原理:物体排开水的重力等于物体所受浮力;
3、物体沉浮条件:物体悬浮时的浮力等于重力(排开水的体积等于物体体积),物体的密度等于液体的密度,物体漂浮表明浮力等于重力(排开水的体积小于物体体积),物体的密度小于液体的密度,物体下沉时重力大于浮力(排开水的体积等于物体体积),物体的密度大于液体的密度。
23.
假设容器的底面积为S,由图甲、乙可知,梨在水中受到的浮力:F浮=ρ水gV排=ρ水gS(h2-h1),
由图乙可知,梨漂浮在水面,根据物体的浮沉条件可知,梨的重力G=F浮=ρ水gS(h2-h1),
假设酱油的密度为ρ酱油,由图丙、丁可知,梨在酱油中受到的浮力:F'浮=ρ水gV'排=ρ酱油gS(h4-h3),
由图丁可知,梨漂浮在酱油中,根据物体的浮沉条件可知,F'浮=G,
即ρ酱油gS(h4-h3)=ρ水gS(h2-h1),
解得:酱油的密度:。
根据甲、乙两图,利用阿基米德原理求出梨在水中受到的浮力,根据物体的浮沉条件可知梨的重力;
由图丙、丁表示出梨在酱油中受到的浮力,根据物体的浮沉条件可知梨在水中和酱油中受到的浮力相等,据此解出酱油的密度。
24.(1)解: 合金块的重力为
(2)解: 合金块放入锥形瓶内浸没。排开水的体积与金属块的体积相等为
合金块放入锥形瓶内稳定后所受浮力为
(3)解: 图乙中合金块对锥形瓶底的压力为
合金块对锥形瓶底的压强为
(4)解: 合金块放入锥形瓶前后,液面上升的高度为
水对锥形瓶底的压强变化为
水对锥形瓶底的压力变化量为
(1)已知正方体合金块的质量,根据G=mg求合金块的重力;
(2)已知正方体合金块的边长,根据V=L3求合金块的体积,合金浸没在水中,排开水的体积等于它的体积,根据F浮=ρ液gV排求合金块放入锥形瓶内稳定后所受浮力大小;
(3)根据力的平衡条件求瓶底对合金块的支持力,根据力的相互性可知合金块对瓶底的压力,根据求合金块对锥形瓶底的压强;
(4)合金块放入锥形瓶后,根据V=Sh求水面高度的变化量,根据p=P液gh求水对瓶底的压强变化 量,根据求水对锥形瓶底的压力变化量。
25.(1)解: 容器底部受到的压强
(2)解: A处于漂浮状态,A受到的浮力
由得A排开水的体积
A漂浮时浸入水中的深度
(3)解: A、B悬浮时,受到总浮力
B受到的重力
B开始运动时,A上表面与B下表面重合,距容器底距离
A、B刚好浸没时,液面上升的高度
B刚好浸没时,下表面距容器底的距离
B开始运动到刚好浸没时运动的距离
B的重力做功
(1)根据p=ρ液gh求容器底部受到水的压强;
(2)根据物体的漂浮条件求出A漂浮时受到的浮力,根据F浮=ρ液gV排求出此时A排开水的体积,根据V=Sh求出此时A浸入水中的深度;
(3)当AB悬浮时,将二者的体积相加得到排开水的总体积,然后根据阿基米德原理计算此时它们受到的浮力,接下来减去A的重力计算出B的重力。
B开始运动时,A上表面与B下表面重合, 计算出距离容器底部的距离和液面上升的高度。再计算出B刚好浸没时下表面到容器底部的距离,进而计算出B从开始运动到刚好浸没通过的距离,最后根据W=Gh计算B的重力做功即可。
26.(1)解: 质量为18kg的水的重力
(2)解: 由图像乙可知,当A容器中注水4kg时,水对A容器底的压强为1×103Pa,此时A容器中水的深度
此时A容器中水的体积
A容器的底面积
由图像乙可知,当注入水的质量为4~6kg时,水对A容器底部的压强不变,说明A容器此时水面到达细管位置,水流入B容器,当B容器水面到达细管位置时,注入B容器中水的质量
当B容器中注入水的质量为2kg时,即
此时B容器中水的深度与A容器中水的深度相同,则B容器的底面积为A容器底面积的一半,即
当往整个装置中注入水的质量为5kg时,注入B容器中水的质量
此时B容器中水的体积
此时B容器中水的深度
水对B容器底部的压强
(3)解: 冰球放入A容器后水面刚稳定时B容器中水的深度增加了0.03m,则A容器中水的深度增加了0.03m,则冰球浸入水中的体积
冰球处于漂浮状态,则所受浮力等于重力,则冰球的重力
冰球的质量
冰球的总体积
冰的体积
冰球内部气泡的总体积
(1)根据重力公式G=mg计算18kg水的重力;
(2)当注水4kg,此时水对A的容器为103Pa,根据P=ρgh计算A容器的深度h;根据密度公式计算水的体积,A容器底面积,据图可知当注入水的质量为4~6kg时,水对A容器底部的压强不变,说明A容器此时水面到达细管位置,注入B容器中水的质量,当B容器中注入水的质量为2kg时,即,且B容器中水的深度与A容器中水的深度相同,所以,当往整个装置中注入水的质量为5kg时,注入B容器中水的质量,根据密度公式计算B容器中水的体积,B容器中水的深度,根据压强公式计算水对B容器底部的压强。
(3) 冰球放入A容器后水面刚稳定时B容器中水的深度增加了0.03m,所以A容器中水的深度增加了0.03m,则冰球浸入水中的体积,此时冰球处于漂浮状态,则冰球的重力,根据重力公式计算冰球质量,冰球的总体积,结合密度公式计算冰的体积,所以冰球内部气泡的总体积。
27.(1)解:
(2)解:
(3)解:
(1) 长方体空鱼缸的重力G为64N , 鱼缸与桌面接触面积S为0.16cm2, 根据F=Ps计算 空鱼缸对水平桌面的压强。
(2) 鱼缸中注入h为0.2m深的水 ,根据P=ρgh计算 放入假山石前,水对鱼缸底的压强。
(3) 假山石的体积V石为,水的密度,根据浮力公式计算计算 浸没在水中的假山石受到的浮力 。
28.(1)解: 空塑料瓶的重力为
由于漂浮,空载时塑料瓶受到的浮力为。
(2)解: 当塑料瓶满载时,浸入水中深度最大,此时塑料瓶排开水的体积为;
此时塑料瓶受到的浮力为
此时所载物体的重力为;
浮力称的最大称量值为。
(3)解: 浮力秤空载时和最大称量时塑料瓶浸入水中的体积变化量为
水槽内水面高度差为。
(1)空载时塑料瓶受到的浮力等于塑料瓶的重力,使用公式F浮=G计算;
(2)先根据求出瓶身最大排水体积,然后根据阿基米德原理F浮=ρ水gV排求出最大浮力,然后根据平衡力的知识计算所载物体的重力,再根据计算出最大称量质量;
(3)先求出浮力秤空载时和最大称量时塑料瓶浸入水中的体积变化量,再用体积变化量除以水槽底面积即可得到结果。
29.(1)解: 根据阿基米德原理,浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开液体所受的重力,即
由图乙可知,小桶的重力
当时,排开水的重力
所以正方体E受到的浮力
(2)解: 由图乙可知,正方体E从刚接触水面到刚好完全浸没所用的时间
正方体E完全浸没时排开水的重力
根据,可得正方体E的体积
所以正方体E的边长
升降台匀速上升的速度
(3)解: 当 时,正方体 E 已经完全浸没在水中,此时力传感器 A 的示数 。由前面计算可知
如果正方体 E 的密度大于水:根据称重法可得正方体 E 的重力
正方体 E 的质量
正方体 E 的密度
如果正方体 E 的密度小于水:根据称重法可得正方体 E 的重力
正方体 E 的质量
正方体 E 的密度
故正方体 E 的密度为 或
(1)由图乙可知,小桶的重力,根据平衡力的知识计算排开水的重力,根据阿基米德原理可求得正方体E受到的浮力;
(2)由图乙可知,正方体E从刚接触水面到刚好完全浸没所用的时间和正方体E完全浸没时排开水的重力,由F浮=ρ液gV排可求得正方体排开水的体积,即为正方体的体积,然后可求得正方体E的边长,由速度公式可求得升降台匀速上升的速度;
(3)当t=10s时,正方体E已经完全浸没在水中,此时力传感器A的示数FA=2N,
分两种情况讨论:如果正方体E的密度大于水,根据称重法可得正方体E的重力G=F浮总+FA,然后可求正方体E的质量,由密度公式可求正方体E的密度:
如果正方体E的密度小于水,根据称重法可得正方体E的重力:G'=F浮总-FA,同理可求得正方体E的密度。
30.(1)解: 由题意可知工件的质量为90kg,则工件的重力为:
答:工件的质量为900N。
(2)解: 工件一半浸入清洗液时,进入深度为为:
则底部受到压强为:
答:清洗液对工件底部的压强为2000Pa。
(3)解: 工件完全浸入清洗液,工件受到的浮力为:
则工件的体积:
工件的底面积为:
答:工件的底面积为0.05m2。
(4)解: 刚好浸没时
液面上升的高度为:
工件下降的高度为:
工件从接触液面到刚好完全浸入所用的时间为 :
设池底部压强为p,经过时间为t,则有
则
代入数据解得
池底部压强为,
答:若工件以1.5cm/s的速度浸入清洗液,则工件从接触液面到刚好完全浸入所用的时间为25s,清洗液对清洗池底部的压强随时间变化的关系式是p=4800+40t,0≤t≤25。
(1)已知工件的质量,根据G=mg求工件的重力;
(2)由工件的高度可知工件一半浸入清洗液时,工件底部的深度,根据P=ρgh求出工件底部受到的压强;
(3)已知工件的重力和绳对工件的拉力,根据求出工件受到的浮力;工件完全浸入清洗液,根据求出工件的体积;已知工件的高度,根据求出工件的底面积;
(4)根据V=Sh得到工件刚好浸没,液面上升的高度,工件下降的高度为浸入的深度和液面上升的高度之差,根据速度变形公式得到时间;
设池底压强为p,经过的时间为t,根据V=Sh得到排开液体的体积的关系,得到升高的高度和时间的关系,根据液体压强的公式得到池底压强的关系。
31.(1)解:将物块A放置于玻璃容器底部中央,物块A对容器底部的压力为
则物块A对容器底部的压强
(2)解:当水深为时,水对容器底部的压强
注入水的体积为
(3)解:质量为的水体积为
A的体积为
容器的容积为
B的密度为
则B漂浮时受到的浮力为
则B漂浮时排开水的体积为
B漂浮时浸入水中的深度为
因为
所以最终B漂浮;因为
所以水没有溢出,则最终水深为
则B上升的高度为
则水对物块B所做的功
(1)A的质量为1kg,根据重力公式计算其重力G=mg,结合压强公式计算物块A对容器底部的压强。
(2)根据P=ρgh计算水深为时,水对容器底部的压强;
(3)根据密度公式计算质量为的水体积,B的密度;A的体积为,容器的容积为,分析可知B的密度小于水的密度,所以B漂浮,受到浮力等于重力,即;
则B漂浮时排开水的体积为,B漂浮时浸入水中的深度为,据此分析B最终的浮沉状态。以及水最终是否溢出和最终水深,所以B上升的高度为,根据计算水对物块B所做的功。
32.(1)解: 物体C的重力
(2)解: 当物体C完全浸没时,由图可知杆对物体C的压力为
对C受力分析,C受到重力、浮力和压力,则
则物体C完全浸没时排开水的体积
(3)解: 当物体C的下端刚好露出水面时,水舱模型内剩余水的体积
C的下端距离水舱模型底部的距离
当力传感器示数为时
①若杆对物体C的压力为
对C受力分析,C受到重力、浮力和压力,则
物体C排开水的体积
物体C浸在水中的深度
此时水的深度为
则水对水舱模型底部的压强
②若杆对物体C的拉力为
对C受力分析,C受到重力、浮力和拉力,则
解得
物体C排开水的体积
物体C浸在水中的深度
此时水的深度为
则水对水舱模型底部的压强
所以当力传感器示数为2N时,水对水舱模型底部的压强为或。
(1) 物体C是质量,根据G=mg计算其重力;
(2)当物体C完全浸没时,杆对物体C的压力为,对其进行受力分析可知;结合浮力公式计算C完全浸没时排开水的体积;
(3) 当物体C的下端刚好露出水面时,水舱模型内剩余水的体积为;所以C的下端距离水舱模型底部的距离,当力传感器示数为时,分2种情况进行考虑:
①若杆对物体C的压力为,对C受力分析,则;物体C排开水的体积;物体C浸在水中的深度;此时水的深度为;根据压强公式计算水对水舱模型底部的压强。
②若杆对物体C的拉力为,对C受力分析,;物体C排开水的体积;物体C浸在水中的深度,此时水的深度为;根据压强公式P=ρgh计算水对水舱模型底部的压强。
33.(1)解: 由阿基米德原理可知,“雪龙”号满载时受到的浮力
(2)解: 水面下5m深处船壁受到海水的压强
(3)解: “雪龙”号做匀速直线运动的速度为
由和得
则“雪龙”号主机提供的动力
(1)考察船漂浮,所以重力等于浮力,即;
(2)根据压强公式P=ρgh计算 水面下5m深处船壁受到海水的压强 ;
(3)“雪龙”号做匀速直线运动的速度为v;由和得,所以“雪龙”号主机提供的动力。
34.(1)解: 浮筒A的质量0.3kg,g取10N/kg,浮筒A的重力
(2)解: 当水位最低1.4m时,两端电压达到4V,因为与串联,电源电压恒为6V,
所以两端电压;
电路电流为;
则。
(3)解: 当到达最高水位1.6m时,设浮筒A上升距离为h,根据图乙可知此时弹簧拉力为
当浮筒A受到的浮力为
则有
即
解得:
浮筒A底部受到水的压强
当水位上升到最高1.6m时,两端电压达到2V,因为与串联,电源电压恒为6V,所以两端电压
电路电流为
则
即滑片上升0.15m,阻值增加了
因为电阻丝阻值与接入电路中的长度成正比,则接入电路中的总长度为
(4)解: 由(3)可知,水位高度H 时有
解得:
当水位高度为H 时,电路总电阻为
电路中电流其中()
(1)根据G=mg求出浮筒A的重力;
(2)由图甲可知两电阻串联;由题意可知当水位降到最低1.4m时R1两端电压为4V,根据串联电路的电压特点和欧姆定律求出此时R2的阻值;
(3)由题意可知当水位升高到1.6m时R1两端电压为2V,根据串联电路的电压特点和欧姆定律求出此时R2的阻值,进而求出水位由1.4m升高到1.6m时,R2接入电路的电阻变化量;
根据图乙表示出弹簧拉力大小与伸长量Δx的关系,根据力的平衡条件表示出水位达到1.6m时A的重力与A受到的浮力和拉力之间的关系,结合F浮=ρ液gV排和V=Sh求出此时弹簧伸长量的变化值,进而求出此时浮筒A底部到水面的深度,根据p=ρgh求出浮筒A底部受到水的压强;根据水位从1.4m升高到1.6m时R2接入电路的电阻变化量和电阻丝长度的变化量求出R2阻值与接入电路中的长度关系,进一步求出此时R2接入电路中的总长度;
(4)根据力的平衡条件表示出水位为H时A的重力与A受到的浮力和拉力之间的关系,结合F浮=ρ液gV排和V=Sh表示出此时弹簧的伸长量,进而表示出R2接入电路的电阻,根据串联电路的电阻特点和欧姆定律表示出水位高度在1.4m到1.6m时,电路中电流I与水位高度H的函数关系式。
35.(1)解: 航海器漂浮在水面上,根据浮沉条件可知浮力与重力大小相等,即
排开水的体积为
(2)解: 卸掉重2×105N的设备,航海器剩下的重力为
由图丙可知航海器底部到水面的最大距离为,此时排开水的体积最大;上方三棱柱浸在水中的深度为
即CG=3m,如上图所示,作AB边上的高CD,△ABC中,AB=8m,AC=BC,△ABC为等腰三角形,等腰三角形底边上的高为底边的中线,则AD=BD=4m,则△CDB为等腰三角形,则CD=4m,△ABC与△ECF相似,根据三角形相似有,即
则,上方三棱柱排开水的体积为
代入数据得,清掉泥沙,下方三棱柱排开水的体积为,航海器所受最大浮力为
浮力小于重力,所以搁浅位置24小时内,航海器不能浮起来。
(1) 航海器漂浮在水面上,此时重力等于浮力,根据浮力公式计算排开水的体积;
(2)卸掉重2×105N的设备,据此计算航海器剩下的重力为,知航海器底部到水面的最大距离为,据此计算上方三棱柱浸在水中的深度h,据图分析结合相似三角形可知
,据此求解,上方三棱柱排开水的体积为,求解排开水的体积V,清掉泥沙,下方三棱柱排开水的体积为,根据浮力公式P=ρgV排航海器所受最大浮力,分析和重力的大小关系,分析是否能漂浮。
36.(1)钢的质量:
答: 钢的质量为790kg;
(2)根据阿基米德原理可得,轮船满载时所受的浮力:
答: 轮船满载时所受的浮力为
(3)解:轮船底部受到的海水压强:
根据 可得,轮船底部受到的压力:
答: 轮船底部受到的压力为
(1)根据m=ρv计算钢的质量;
(2)船只漂浮,所以重力等于浮力,即轮船满载时所受的浮力: ;
(3)根据P=ρgh计算轮船底部受到的海水压强,根据 计算轮船底部受到的压力。
37.(1)解: 航行的距离:
答:如果汽车用7.2km/h速度在水中航行30min,它航行的距离为3.6×103m;
(2)解: 车底受到水的压强:
答:当汽车在水中航行时,若车的底部距水面0.8m,车底受到水的压强为8×103Pa;
(3)解: 汽车在水中满载航行时受到的浮力:
答: 汽车在水中满载航行时受到的浮力为4×104N。
(1)根据s=vt计算汽车航行的距离;
(2)利用P=ρgh计算车底受到水的压强;
(3根据阿基米德原理F浮=G排=m排g计算受到的浮力。
38.(1)解: 该船受到的总重力:
答:该船受到的总重力为4.12×107N;
(2)解: 船只漂浮,静止时,受到浮力为:
则排开海水的体积:
答:静止时排开海水的体积为4×103m3;
(3)解: 发动机完全燃烧100kg燃油放出的热量:
答:发动机完全燃烧100kg燃油放出的热量为4.3×109J。
(1)已知船的总质量,根据G=mg求该船受到的总重力;
(2)船静止时,漂浮在海面上,根据二力平衡条件F浮=G可知船所受的浮力大小,根据阿基米德原理F浮=ρ液gV排求出该船静止时排开海水的体积;
(3)已知燃油的质量,根据Q放=mq计算发动机完全燃烧100kg燃油放出的热量。
39.(1)解: 当容器内水的深度为,容器底所受压强
(2)解: 当容器内水的深度时,杯子排开水的体积
根据阿基米德原理,杯子此时所受的浮力
此时杯子对容器底部的压力刚好为零,即
杯子的质量
(3)解: 由题意可知:杯中水的重力等于增加的浮力,即,由此可得
代入数据
解得,杯子中水的体积
当杯口与容器内的水面相平时,杯子排开水的体积
组成杯子的材料的体积
杯子材料的密度
(4)解: 杯子注满水后,杯子的总重力
杯子对容器底的压力
注满水时杯子对容器底部的压强
解法二:
继续向杯子中注水直至注满,此时杯子浸没于水中,即,注满水时杯子对容器底部的压强
(1)已知深度,根据压强p=ρ液gh计算;
(2)根据漂浮的条件结合阿基米德原理计算杯子的质量;
(3)根据两次都是压力为0,结合增大的水的重力等于浮力,结合阿基米德原理计算杯子的体积,根据密度公式计算;
(4)根据注满水计算总重力,结合压力等于重力减去浮力,根据压强公式计算。
40.(1)空载
(2)解: 在水深5000m处海水对钻头的压强
(3)解: 井架对甲板的压力。
井架对甲板的压强
(4)解: 当装载货物时,根据阿基米德原理,货物重力
则货物排开液体
,当船吃水深度为时,船浸在水中船头梯形的面积
船浸入水中的体积
船空载时排开水的体积
空载时,船浸在水中船头的梯形的面积
空载时,船浸在水中的梯形的面积
解得,只要船在空载时能通过大桥,就能始终确保安全通行,旗杆的最大高度
(1)题目中提到“梦想”号钻探船上有高耸的井架,出海执行任务时需要通过大桥。为了确保安全通行,我们需要考虑船只在最不利情况下的高度。船空载时,船的整体重力小,排开液体体积小,吃水深度浅,船露出水面高;满载时,整体重力大,排开液体体积大,吃水深度深,船露出水面低;所以只要空载时能通过大桥,就能始终确保安全通行
(1)为了确保安全通行,我们需要考虑船只在最不利情况下的高度;
(2)根据p=ρgh求出深度为5000m处海水的压强;
(3)根据G=mg算出井架的重力,井架对甲板的压力等于自身的重力,根据压强公式计算井架对甲板的压强;
(4)先计算装载货物时排开液体的体积,根据θ=45°算出船浸入水中的体积,进而算出空载体积和高度,旗杆的最大高度等于桥离水面的高度减去空载的高度。
41.(1)等于
(2)增加重物质量
(3)浮力秤的刻度转换基于阿基米德原理
增加质量m时,需额外排开水的体积
由平衡条件可知
化简得。
(4)小羽的饮料瓶上下粗细不同非圆柱形,但刻度均匀标注。实际浸入深度与排开水的体积不成线性关系,若瓶身向上渐扩,相同刻度下实际排开水的体积大于计算的圆柱形瓶的体积,真实值大于测量值,故制作的浮力秤所称出的物体质量比真实值偏小。
(1)瓶体呈竖直状态,且与重物整体漂浮,根据物体漂浮的条件可知,此时秤体所受浮力大小等于其重力大小;
(2)图甲中秤体在水中的位置尚未满足标记刻度的条件,说明称体排开水的体积较小,说明称体所受的浮力较小,由于称体与重物整体漂浮,根据F浮=ρgV排=G总可知,可以增加重物的质量,即增大物体的重力来增大称体所受的浮力,使称体排开水的体积增大,达到标记刻度的条件,故调整建议为:增加重物质量。
(3)浮力秤的刻度转换基于阿基米德原理
增加质量m时,需额外排开水的体积
由平衡条件可知
化简得
(4)小羽的饮料瓶上下粗细不同非圆柱形,但刻度均匀标注。实际浸入深度与排开水的体积不成线性关系,若瓶身向上渐扩,相同刻度下实际排开水的体积大于计算的圆柱形瓶的体积,真实值大于测量值,故制作的浮力秤所称出的物体质量比真实值偏小。
(1)物体处于漂浮状态,根据浮沉条件可知,浮力等于重力;
(2)图甲中重物的质量小,秤体浸入水中过浅,可以增加重物的质量使秤体浸入深度增加;
(3)根据阿基米德原理和漂浮条件计算瓶身上刻度1cm处所对应的质量标度;
(4)根据实际排开水的体积和计算式中排开水的差异判断。
42.(1)
(2)
(3)
(1)如图,带有秤盘的圆柱形浮体竖直漂浮在水中,浮体浸入水中的深度为h0,
则浮体和秤盘的总重力为G0=F浮0=ρ0gV排0=ρ0gS0h0;
则浮体和秤盘的总质量为;
(2)浮力秤始终漂浮,浮力等于重力,则ΔF浮=ΔG;
则有ΔG=m1g=ρ0gS0Δh,
解得:;
(3)从浮力秤恰好漂浮到外筒底部受到水的压强为p1时,
加入的水的重力为ΔG水=ΔF=ΔpS=(p1-ρ0gh0)×3S0;
则称量的物体质量最大时,浮力秤深度变化量为
;
结合(2)中解析式则有;
解得:最大测量值。
(1)根据漂浮时浮力等于重力,结合阿基米德原理计算;
(2)根据漂浮时,增大的浮力等于增大的重力,结合阿基米德原理列方程计算;
(3)根据压强和底面积计算压力,根据质量最大时,结合浮沉条件与阿基米德原理计算浮力秤深度的变化,结合深度与质量的关系计算。
21世纪教育网(www.21cnjy.com)
一、选择题
1.(2025·武威) 小栋了解到伽利略温度计的测温原理后,想自己动手设计一个粗略测温的装置,他的设计思路如下:在密闭的玻璃容器中装上一种密度会随温度升高而减小的特殊液体,液体中有5个体积相等、密度不同且标有温度示数的小球,小球不吸收液体且热胀冷缩可以忽略不计,当有小球悬浮时,悬浮小球上标有的温度值就是当前环境的温度。如图所示,是这个测温装置的示意图。其中小球3上所标温度值为25℃,相邻标号的小球上所标的温度值间隔为2℃,则下列说法正确的是( )
A.27℃时,小球2处于漂浮状态
B.小球2在27℃时所受的浮力小于25℃时所受的浮力
C.若有3个小球漂浮,2个小球沉底,则环境温度在23℃至25℃之间
D.若要增大该装置能测得的最高温度,可增加一个与小球5体积相等但质量更大的小球
2.(2025·凉山) 《天工开物》中记录了我国古代劳动者煮海水制盐的方法,对用于制盐的海水密度有严格要求。关于海水等级的测评,《熬波图咏》中谈到,可以用莲子制备成四颗不同标准的“浮子”来测定海水等级。测定时,浮起的“浮子”数量越多,待测海水的等级越高(一等海水密度最大等级最高、二、三、四、五等依次次之)。若将以上四颗“浮子”放入盛有待测海水的竹管内,“浮子”的沉浮情况如图所示,下列选项正确的是( )
A.竹管内待测的海水为一等海水
B.①号“浮子”的重力比其它三颗“浮子”大
C.①号“浮子”的密度比其它三颗“浮子”大
D.若竹管内改盛四等海水,①号“浮子”所受浮力不变
3.(2025·烟台) 如图所示,小明洗碗时发现,向漂浮在水面上的碗中加水,碗浸入水的深度越来越大,当水量增加到一定程度时,碗浸没水中,直至沉底。假如碗里水的质量是缓慢均匀增加的,则下列关于碗受到的浮力随时间变化规律的图像可能是( )
A. B.
C. D.
4.(2025·湖南) 小勇在厨房煮鸡蛋时,由观察到的现象联想到的物理知识,正确的是( )
A.鸡蛋浸入水中的体积越大,所受浮力越大
B.鸡蛋沉入水底静止时,所受浮力大于重力
C.给水加热,主要是通过做功的方式增大水的内能
D.锅盖被水蒸气顶起的过程与内燃机的压缩冲程,发生的能量转化相同
5.(2025·苏州)用柱形水槽、柱形塑料杯(含配重)、质量已知的砝码和水,可制作测量物体质量的装置.使用时,在竖直漂浮的塑料杯中放入待测物体,杯子仍竖直料林漂浮,根据制作好的标尺便可读出待测物体的质量。制作标尺时,通过在杯中放入砝码进行质量标注(杯子竖直漂浮)。如图所示,标注的方式有三种:
①在水槽外壁,用水面高度h1的变化标注;
②在塑料杯内壁,用杯子浸人水中的深度h2的变化标注;
③在水槽外壁,用杯底所装指针离槽底的高度h3的变化标注。
若水槽和塑料杯的底面积分别为225cm2和85cm2,三种标尺上相同距离的刻线问对应的物体质量变化分别为 m1、 m2,和 m3。则
A. m1> m2> m3 B. m2> m1=m3
C. m1> m3= m2 D. m3> m1> m3
6.(2025·眉山) 水平桌面上的甲、乙两个相同圆柱形容器,内装不同液体。将两个相同小球分别放入甲、乙两容器中,小球静止时如图所示。若两容器底部所受液体压强相等,则下列判断正确的是( )
A.两容器中液体密度相等
B.两容器所装液体的质量相等
C.甲容器对桌面的压强小于乙容器对桌面的压强
D.甲容器中小球所受浮力大于乙容器中小球所受浮力
7.(2025·遂宁) 2024年12月,我国春节申遗成功。欢度春节期间,人们有“放鞭炮”“舞龙狮”“逛庙会”“吃汤圆”等习俗。关于春节习俗中的物理现象,下列描述错误的是( )
A.鞭炮爆炸与内燃机做功冲程的能量转化方式相同
B.舞龙狮时力改变了物体的运动状态
C.庙会上各种小吃香气四溢是一种扩散现象
D.汤圆漂浮在水面上时受到的浮力大于重力
8.(2025·北京市)某小组设计了水箱自动控制进水装置,如图所示。水箱内的圆柱形金属控制棒用不可伸长的细线悬挂在力传感器下面,并始终浸在水中,通过它对力传感器拉力的大小触发开关,控制水泵自动进水。用水时,水箱内水位降低,当到达最低水位时,力传感器所受拉力等于F1,触发开关,水泵开始持续向水箱注水;当水位到达最高水位时,力传感器所受拉力等于F2,再次触发开关,水泵停止向水箱注水。若进水过程中同时用水,相同时间内进水量大于出水量。已知控制棒质量为m,水的密度为ρ水。下列说法正确的是( )
A.控制棒受到的浮力最大时,排开水的体积为
B.控制棒受到的浮力的变化量最大为mg-F2
C.力传感器受到的拉力大小在F1与F2之间时,说明水箱正在进水
D.缩短悬挂控制棒的细线,可使水箱中的最高和最低水位均升高
9.(2025·山东) 小华在相同气球内装上不同配重做了两个“小鱼”。“小鱼”甲的质量大于“小鱼”乙的质量。注射器可以通过连接“小鱼”的软管对“小鱼”进行抽气和充气,从而改变“小鱼”的体积。初始时,两“小鱼”在水中处于静止状态,如图所示。忽略空气重力及软管对“小鱼”的作用力。“小鱼”所受浮力分别用F甲、F乙表示。下列说法正确的是( )
A.对甲充气,甲上浮,再次静止时F甲小于F乙
B.对甲抽气,甲下沉,再次静止时F甲一定小于F乙
C.对乙充气,乙再次静止时所受浮力比初始时的浮力小
D.对乙抽气,乙再次静止时所受浮力可能等于初始时的浮力
10.(2025·陕西)研学活动中,小明捡到一块石头。他用电子秤和玻璃杯测量其密度,测量过程如图所示。下列判断不正确的是(不计绳子的质量和体积,水的密度为1g/cm3,g取10N/kg) ( )
A.根据本次实验数据,可得出石头密度最准确的测量值为3.125g/cm3
B.从水中取出石头时,带出了1g的水
C.从水中取出石头时,带出的水不会影响密度的测量值
D.石头沉在水底时,杯底对石头的支持力为0.24N
二、填空题
11.(2025·凉山) 2025年5月10日,代号“鲲龙”的水陆两栖飞机AG600,批产首架机总装下线。这是我国自主研制的全球最大的水陆两栖特种用途飞机。“鲲龙”飞行时机翼上方受到空气的压力 下方受到空气的压力(选填“大于”“小于”或“等于”)。如图甲所示,匀速飞行的“鲲龙”在投水灭火时,其动能会 (选填“变大”“变小”或“不变”)。“鲲龙”执行海上救援任务时,可一次性救援50名遇险人员。在海上救援时,“鲲龙”静止在水面,如图乙所示,若此时遇险人员被救上“鲲龙”,它受到的浮力 (选填“变大”“变小”或“不变”)。
12.(2025·遂宁) 2024年12月,我国自主研制建造的076型两栖攻击舰首舰——“中国人民解放军海军四川舰”正式下水,该舰满载排水量(排开水的质量)4万余吨。若以满载排水量4万吨来计算,该舰满载时所受浮力大小为 N。不考虑燃料质量变化,该舰由海水密度较小的近海驶向海水密度较大的远海区域时,排开海水的体积将 (选填“变大”、“变小”或“不变”)。(g取10N/kg)
13.(2025·黑龙江) 小宁同学把一个质量为50g的木块放在水中,木块漂浮时有的体积露出水面,则这个木块受到的浮力是 N,它的密度是 g/cm3。
14.(2025·齐齐哈尔) 某材料不吸收液体,在酒精或盐水中均不溶解,且不与酒精或盐水发生化学反应,用该材料制成重的实心球。若将球投入足够多的酒精中,当球静止时,受到的浮力大小是 ;若将球投入足够多的盐水中,当球静止时,受到的浮力大小是 N。(已知,,)
15.(2025·陕西)小明想测量一个长方体物块的密度,他用细线提着物块缓慢放入盛有水的杯中,如图-1所示,压力传感器的示数随物块浸入深度的变化关系如图-2所示。整个过程中物块受到浮力的变化情况是 ,已知物块的质量为2.4,则物块的密度为 。剪断细线、当物块静止后压力传感器的示数为 N。(水的密度为,g取10)
三、实验探究题
16.(2025·扬州)小明发现冰块在不同饮料中熔化快慢不同,决定探究影响冰块熔化快慢的因素.
(1)相同的0℃的冰块在某液体中熔化得快,说明相同时间内,冰块在该液体中吸收的热量 (选填“多”或“少”).
(2)若将两个相同的0℃的冰块分别放入水和浓盐水中,所受浮力分别为F 、F盐水,与液体接触面积分别为S水、S盐水,则 F水 F盐水,S水 S块水.
(3)为探究冰块熔化快慢与接触面积的关系,下列两个方案,应选用方案 .
方案一:如图1、2,取两个相同的0℃的冰块,一块直接放入水中,另一块竖切成4 小块放入相同的水中,记录冰块完全熔化的时间分别为t1、t2.
方案二:如图3.4,在装满相同温度的水和浓盐水的玻璃杯中,分别放入相同的0℃的冰块,盖上杯盖使冰块保持浸没,记录冰块完全熔化的时间分别为t3、t4.
(4)①采用方案一进行实验,发现 ,得出的结论是 .
②采用方案二进行实验,发现 ,得出的结论是 .
(5)在用方案二进行实验前,小明根据“向积雪的公路上撒盐,盐能尽快地融雪”,预测冰块在浓盐水中熔化得更快.他的推理是否正确 ,请说明理由: .
17.(2025·江西)亲爱的同学,请你运用所学的物理知识解答下列问题。
(1)如图甲所示,某同学遵照“红灯停,绿灯行,斑马线上安全行”的交通安全知识行走在上学路上,步长约0.6m,直行通过马路共走了32步,并用秒表先后记录了开始和结束时的时间(如图乙和丙所示)。则马路的宽度约为 m,该同学通过马路的时间为 s,速度约为 m/s。
(2)如图所示,重力为1.5N的物体静止在水中。弹簧测力计的示数为 N,物体所受浮力的大小为 N
(3)某同学在“探究水在沸腾前后温度变化的特点”实验中,放置温度计时(如图所示),其操作错误是将温度计的玻璃泡接触了 :纠正错误后继续实验,得出水沸腾时的特点:水持续吸热,温度保持 .
18.(2025·新疆) 小华在实验室里测量土豆的密度,实验操作如下:
(1)用 (选填“天平”或“测力计”)测出洗净的土豆样品的质量为220g;
(2)用细线系住土豆样品,缓慢放入装有400mL水的量筒内,土豆排开的水的体积越大,土豆受到的浮力越 (选填“大”或“小”);土豆最终在量筒内静止时如图所示,则土豆样品的密度为 g/cm3;
(3)小华通过查阅资料知道,土豆密度越大,淀粉含量越高,土豆品质越好。可以采取如下方法来评定土豆的品质:先用弹簧测力计测量出土豆样品的重力G;然后把土豆样品浸没在水中(未接触容器底)静止时,读出测力计的示数F,则的值越 (选填“大”或“小”),土豆品质越好。
19.(2025·泸州)实践出真知。“九章”社团的同学们利用所学知识进行跨学科实践——自制密度计。
(1)他们用铁钉插入粗细均匀、横截面积为0.2cm2的吸管并密封,制作了第一代密度计。使用铁钉的目的是使吸管重心降低、在液体中竖直 ,测试时将其放入密度为 1.0g/cm3的清水中,测得它的吃水深度为10.5cm;取出再放入盐水中,测得它的吃水深度为10.0cm, 则盐水的密度为 g/cm3,发现两次吃水深度相差很小,同学们猜想可能是吸管横截面积太小的缘故:
(2)于是, 他们用横截面积较大、粗细均匀的柱形瓶做了第二代密度计,测试时发现它在清水和上述盐水中的吃水深度差与第一代密度计几乎一样,老师提出:根据密度计在两种液体中受到液体对它的力相等,可推出这种粗细均匀的密度计在清水和盐水中的吃水深度的比值关系是别: 用、表示);
(3)同学们围绕怎样增大吃水深度差这一问题,结合前两次的制作经验,将设计思路和数据输入某AI软件,设计了如图所示的第三代密度计,若第三代密度计在清水中的吃水深度仍为10.5cm, 则它在上述盐水中吃水深度为 cm. 若它在某种液体中的吃水深度为 15.0cm, 则这种液体的密度为 g/cm3.(以上结果保留两位小数)
20.(2025·齐齐哈尔) 小明在得出浸在液体中的物体受到的浮力大小跟物体本身因素无关的结论后,进一步探究“浮力的大小跟哪些因素有关”;
表一
实验次序 液体种类 物体下表面浸入水中的深度/cm 弹簧测力计的示数/N
1 水 0 2.7
2 2 2.2
3 4 1.7
4 6 1.7
… … …
(1)如图甲所示,小明将装有适量水的烧杯放在盘中,用手把空的饮料罐沿竖直方向逐渐按入水中。此过程中,手感受到饮料罐受到的浮力逐渐增大。小明通过分析现象提出猜想,浮力大小可能跟物体浸入液体的深度或物体浸在液体中的 有关。通过其他生活经验,小明还猜想浮力的大小可能跟液体密度有关;
(2)小明用图乙的实验装置进行实验。将盛有适量水的容器放置在桌面上,正确使用弹簧测力计,将一个长方体铝块(高为)用细线悬挂在弹簧测力计下。使铝块沿竖直方向逐渐下降,缓慢浸入水中。实验过程中,保持弹簧测力计的轴线与铝块的竖直轴线在同一直线上。获取触底前的多组实验数据并记录在表一中;
①分析实验数据可知,铝块受到的重力是 N,第2组实验中铝块受到的浮力是 N;
②分析第1、3、4三组实验数据可知,浮力大小跟物体浸入液体的深度 (选填“有关”或“无关”);
③分析第1、2、3三组实验数据可得出初步结论: ;
(3)小明根据实验的初步结论,设计了用图丙所示装置测量某液体密度的方案:
①将3个空的相同厚底薄壁圆柱形玻璃容器(高为)放入足够深的水槽中,待稳定后,容器A、B、C都保持竖直静止,测得容器A、B、C浸入水中的深度均为;
②向容器B、C中分别缓慢装入 (选填“质量”或“体积”)相等的某液体和水。待稳定后,容器A、B、C保持竖直静止,且未触底。测量容器B、C浸入水中的深度,将容器A、B、C浸入水中的深度记录在表二中;
③分析表二中的数据,通过计算可知,液体的密度 。
表二
容器 A B C
容器浸入水中的深度/cm 6 12 11
21.(2025·长沙) 如图是探究浮力的大小是否跟物体浸没的深度有关的实验过程。
(1)实验时,应先将弹簧测力计在 方向调零;
(2)乙图中物体所受浮力为 N;
(3)请你分析实验数据,判断物体所受浮力的大小是否跟物体浸没的深度有关,并说明理由。
22.(2025·吉林) 学校科技小组进行了“测量小石块密度”的实验。
(1)用天平测小石块的质量,当天平平衡时,右盘中的砝码和标尺上游码的位置如图甲所示,小石块的质量为 g,用量筒和水测得小石块的体积为20cm3,则小石块的密度为 kg/m3。
(2)利用浮力知识,科技小组的同学又用另一种方法测出了小石块的密度。步骤一:如图乙所示,将长方体物块放入柱形盛水容器中,物块漂浮,测出物块浸入水中的长度。
步骤二:如图丙所示,将小石块放在物块上,测得物块浸入水中的长度与图乙相比增加了h1,此时物块受到的浮力与图乙相比
步骤三:如图丁所示,将小石块用细线(细线体积和质量均忽略不计)系在物块下,测得物块浸入水中的长度与图乙相比增加了h2,图丁中水对容器底部的压强 图丙中水对容器底部的压强(填“大于”、“等于”或“小于”)。
根据以上信息可得,小石块密度的表达式为ρ石= (用ρ水、h1、h2表示)。
23.(2025·北京市)某同学利用一个圆柱形容器、一个梨、记号笔、刻度尺和适量的水测量酱油的密度,测量过程如图所示,图中h1、h2、h3、h4分别是梨放入水、酱油前后液面到容器底的距离。已知水的密度为ρ水,则待测酱油的密度ρ酱油= 。(用已知量和测量量表示)
四、计算题
24.(2025·凉山) 如图甲所示,在上、下截面均为圆形的锥形瓶内,装有一定量的水。已知锥形瓶上部分是横截面积为的圆筒,且粗细均匀,底面积为。现将质量为32g,边长为2cm的正方体合金块放入锥形瓶内,水未溢出,如图乙。求:
(1)合金块的重力大小;
(2)合金块放入锥形瓶内稳定后所受浮力大小;
(3)如图乙,稳定后,合金块对锥形瓶底的压强;
(4)合金块放入锥形瓶前后,水对锥形瓶底的压力变化量。
25.(2025·广安)某同学看了我国航空母舰发展简介后对力学产生了浓厚的兴趣。他用底面积为的长方体容器(厚度不计)装一定量的水,将一个重为4N,边长为10cm的正方体A放入容器中处于漂浮状态。如图所示,此时水的深度为18cm。(,g取10N/kg)求:
(1)容器底部受到水的压强;
(2)A漂浮时浸入水中的深度;
(3)若将与A形状体积完全相同的物体B平放在A的正上方,A、B一起向下运动,当静止时一起处于悬浮状态。求A、B一起开始运动到B刚好浸没时,B的重力做的功。(容器足够高,水不溢出,A、B不吸水)
26.(2025·新疆) 如图甲所示,A、B两个薄壁圆柱形容器下半部用细管(体积不计)水平连通后放在水平地面上,将18kg水经A容器缓慢的注入整个装置的过程中,水对A容器底部的压强p与注入的水的质量m的关系如图乙所示。将一个内部有许多小气泡的冰球投入到A容器中(水未溢出),水面刚稳定时冰球露出水面的体积,此时B容器中水的深度增加了。已知冰的密度为,求:
(1)质量为18kg的水的重力;
(2)当往整个装置中注入水的质量为5kg时,水对B容器底部的压强;
(3)冰球放入A容器中水面刚稳定时,冰球内部气泡的总体积V气。
27.(2025·河北)小明利用双休日清理家中的鱼缸。长方体空鱼缸的重力G为64N,小明将鱼缸和假山石清洗干净,放到水平桌面上,鱼缸与桌面接触面积 S为0.16cm2, 向鱼缸中注入 h为0.2m深的水,然后将假山石(不吸水)浸没在水中,如图所示。已知假山石的体积 V石为,水的密度 , g取10N/ kg。
求:
(1)空鱼缸对水平桌面的压强。
(2)放入假山石前,水对鱼缸底的压强。
(3)浸没在水中的假山石受到的浮力。
28.(2025·乐山) 如图所示,某同学用一个上端开口的圆柱形厚底空塑料瓶和装有水的圆柱形水槽制作了一个浮力秤,用于测量质量。空塑料瓶质量为120g,塑料瓶底面积为,水槽底面积为,瓶身能够浸入水中的最大长度为18cm,使用过程中水不溢出,塑料瓶始终漂浮且瓶身保持竖直。已知水的密度为,g取10N/kg,不考虑塑料瓶侧壁的厚度。求:
(1)空载时塑料瓶受到的浮力;
(2)浮力秤的最大称量值;
(3)浮力秤空载时和最大称量时水槽内水面的高度差。
29.(2025·泸州)科创小组的同学设计了如图甲所示的力学综合实验装置,力传感器A上确固定在水平杆上,下端通过竖直轻杆与正方体E相连,水平升降台上放有溢水杯c和力传感器B,小桶D放在力感器B上,溢水杯C中的水面刚好与溢水口齐平,水平升降台匀速上升,当t=0时,正方体E刚好接触水面,之后排开的水全部流入小桶D中,力传感器B的示数FB随时间t变化的关系如图乙所示。已知g=10N/kg.ρ水=1.0x103kg/m3.
(1)当力传感器B的示数FB=5N时, 求正方体E受到的浮力:
(2)求升降台匀速上升的速度:
(3)当t=10s时,力传感器A的示数FA=2N,求正方体E的密度。
30.(2025·宜宾) 某锻造厂利用卷扬机将一圆柱形工件(污垢的质量和体积忽略不计)吊入柱形清洗池中清洗,如图所示。已知工件的质量为90kg,高度为50cm,清洗池底面积为2000,深度为80cm;未放入工件时,清洗液的深度为60cm,密度,。求:
(1)工件的重力;
(2)工件一半浸入清洗液时,清洗液对工件底部的压强;
(3)工件完全浸入清洗液,平衡时绳对工件的拉力为700N,工件的底面积是多少;
(4)若工件以1.5cm/s的速度浸入清洗液,则工件从接触液面到刚好完全浸入所用的时间为多少,写出此过程清洗液对清洗池底部的压强随时间变化的关系式。
31.(2025·广西) 某同学探究不同密度的物块在液体中的特点,如图所示,现有质地均匀,不吸水的正方体物块A和B,其质量分别为和、边长分别为和,以及内部边长为的正方体玻璃容器。已知水的密度。取。求:
(1)将物块A放置于玻璃容器底部中央,物块A对容器底部的压强;
(2)往容器内缓慢注水,物块A不上浮,当水深为时,水对容器底部的压强和注入水的体积;
(3)接着把物块B放在物块A的正上方。再将质量为的水缓慢注入容器。在此过程中,水对物块B所做的功。
32.(2025·德阳) 如图甲所示,“国之重器”起重船起吊重物时,需通过抽水机将一侧水舱里的水抽向另一侧水舱来保持起重船平衡。如图乙所示,小兰设计了一种采用力传感器感知抽水量的长方体水舱模型,水舱中装有的水,其底面积。A是固定在顶端的力传感器,能够显示A对B的压力或拉力的大小;B是质量和体积均可忽略的细直硬杆,不考虑B的形变,B的上端与力传感器A连接,下端与物体C连接;物体C是质量、底面积的圆柱体。用抽水机将水抽出的过程中,力传感器示数的大小随抽出水的体积变化的图像如图丙所示。当物体C的下端刚好露出水面,此时已抽出水的体积。已知。求:
(1)物体C的重力;
(2)物体C完全浸没时排开水的体积;
(3)当力传感器示数为时,水对水舱模型底部的压强。
33.(2025·眉山) “雪龙”号是我国最大的极地考察船,排水量约,吃水深度可达,动力系统中,主机功率。取,,求:
(1)“雪龙”号满载时受到的浮力;
(2)水面下5m深处船壁受到海水的压强;
(3)如图所示,执行科考任务的“雪龙”号在海面破冰前行,假如船以的速度做匀速直线运动,主机能提供多大的动力。
34.(2025·遂宁) 小聪为学校的鱼池设计自动补水装置,实现鱼池中水位处在1.4m到1.6m之间,适宜鱼儿生长。他设计的装置如图甲,L为一根上端固定的轻质弹簧(可视为导线),弹簧拉力大小与伸长量的关系如图乙。塑料圆柱形密闭浮筒A的底面积,高0.2m,质量0.3kg。电源电压恒为6V,,为一根足够长的电阻丝,其阻值与接入电路中的长度成正比,滑片P可随浮筒A竖直上下移动。电压传感器(对电路无影响,未画出)监测两端的电压,当两端电压达到4V,传感器控制注水阀门打开;当两端电压低于2V时,传感器控制注水阀门关闭。通过调试:当水位降到最低1.4m时,浮筒A底部刚好接触水面,滑片P位于的某一位置,注水阀门打开:当水位上升到最高1.6m时,注水阀门关闭。(,g取10N/kg)求:
(1)浮筒A的重力;
(2)水位最低1.4m时的阻值;
(3)到达最高水位1.6m时,浮筒A底部受到水的压强,以及接入电路中的总长度;
(4)小聪还想在电路中串联一个电流表,将其改装为一个水位计,请帮他找出水位高度在1.4m到1.6m时,电路中电流I(单位:A)与水位高度H(单位:m)的函数关系式。
35.(2025·威海) 如图甲所示,某航海器由钢板焊接的两个空心三棱柱组成。侧面为ABCDE;在△ABC中,AB=8m,AC=BC,;在中,底边DE的高为0.9m;两个三棱柱棱的长度均为10m,下方三棱柱体积为6m3,航海器总重(,g取10N/kg,三棱柱体积=三角形面积×棱的长度)
(1)当航海器漂浮在水面上,求排开水的体积。
(2)航海器误入浅水区搁浅,下方三棱柱一部分陷入泥沙,如图乙所示。
为将航海器浮起来,采取了以下措施:卸掉重2×105N的设备,等待涨潮之后清理下面的泥沙。搁浅位置24小时内,航海器底部到水面的距离H随时间变化情况如图丙所示。假设航海器整体始终保持水平,请通过计算判断航海器是否能浮起来?
36.(2025·深圳)如图是深圳号在海上航行,田田同学乘坐了这艘船出海游玩。田田发现这艘船最大吃水高度是9米,最大排水量是70000吨,船上一汽车用钢打造,钢的体积0.1立方米。(已知:钢的密度是 海水密度
求
(1)钢的质量,
(2)求轮船所受的浮力,
(3)船底面积是 ,求轮船底部受到的压力。
37.(2025·黑龙江) 如图,这是一款国产水陆两栖汽车航行技术测试的现场。这辆汽车在水中的最大速度约为8.3km/h。良好的密封技术和防锈处理,使车体的吃水深度达到1.05m,满载时排开水的质量达到4×103kg。求:
(1)如果汽车用7.2km/h速度在水中航行30min,它航行的距离;
(2)当汽车在水中航行时,若车的底部距水面0.8m,车底受到水的压强;
(3)汽车在水中满载航行时受到的浮力。
38.(2025·广东)题图所示是我国自主设计建造的“极地”号破冰调查船,某次任务中,该船的总质量为4.12x106kg.已知g=10N/kg,ρ海水=1.03×103kg/m3,q燃油=4.3×107J/kg.求该船:
(1)受到的总重力:
(2)静止时排开海水的体积:
(3)发动机完全燃烧100kg燃油放出的热量.
39.(2025·绥化) 如图所示,水平桌面上有一个圆柱形薄壁容器。容器内竖立一个圆柱形杯子(材料质地均匀),高为0.09m,底面积为。现只向容器内注水,当容器内水的深度为0.06m时,杯子对容器底部的压力刚好为零;接下来同时向容器内和杯中注水,当杯口与容器内的水面相平时,杯中水的体积是杯子容积的一半,且杯子对容器底部的压力也刚好为零。(整个过程中,杯底与容器底部始终接触但不紧密)求:
(1)只向容器内注水,当水的深度为0.06m时,水对容器底部的压强;
(2)空杯子的质量;
(3)该杯子材料的密度;
(4)继续向杯子中注水,直至注满,此时杯子对容器底部的压强是多少?
五、综合题
40.(2025·云南) 2024年11月17日,我国建造的全球最先进的大洋钻探船“梦想”号正式入列,如图甲所示。它具备11000米超深水钻探能力,有望实现“打穿地壳,进入地球深部”的科学梦想。钻探船上高耸的井架控制钻杆作业,使钻头深入海底钻取岩心。
(1)“梦想”号钻探船上建有高耸的井架,出海执行任务时,要从大桥下通过。只要 (选填“空载”或“满载”)时能通过大桥,就能始终确保安全通行。
(2)求在水深5000m处海水对钻头的压强。取)
(3)科创小组估测井架质量为,井架与甲板接触面积为,求井架对甲板的压强。
(4)为了研究“梦想”号钻探船从桥下安全通行的高度问题,科创小组用两块相同的等腰梯形板材和三块长边均为的矩形板材,制作了如图乙所示的“启航”号实验船,板材不吸水且厚度不计。船底短边,船身高度,,船头竖立有旗杆。将船放入平静的湖水中进行实验,当装载货物时,吃水深度为。若桥离水面的高度,要实验船始终能安全通过此桥,求旗杆的最大高度。(货物高度始终低于旗杆顶部,)
41.(2025·贵州) 某次学校物理社团活动主题是“制作浮力秤”。经思考,小明决定用薄壁硬质饮料瓶、水槽、水、细线及几个质量不同的重物进行制作。他设想,让饮料瓶漂浮于水面,在瓶身上标记出相应的质量刻度线,把待测物体放入瓶中,待水面静止时,根据水面所在刻度线的位置,便可读出待测物体质量。小明进行如下制作:
【任务一】制作秤体
小明切掉饮料瓶底部,用细线将瓶盖与其中一个重物连接,旋紧瓶盖,将瓶体开口向上倒置于水槽中,待其静止后,若瓶体呈竖直状态,且与重物整体漂浮,则秤体制作完成,如图甲所示。此时瓶体便可作为秤盘盛放待测物体。
(1)此时秤体所受浮力大小 其重力大小。
(2)【任务二】标注刻度
小明认为当秤体漂浮,且水面位于瓶体的圆柱状部分时才便于标记刻度。他发现图甲中秤体在水中的位置尚未满足标记刻度的条件。
为满足条件,小明用准备的器材进行调整,请你给他提出调整建议 。
调整完成后,小明先将饮料瓶身与水面齐平处标记为0cm,此处即为质量标度的零刻度线;将饮料瓶取出,再将刻度尺对应的长度刻度值标记在瓶身上;测量出饮料瓶圆柱状部分的横截面积为50cm2,再放入水中,如图乙所示。
(3)接下来,只需将瓶身上所标注的长度刻度值转换为相应的质量标度,便可完成浮力秤的制作。请你计算瓶身上刻度1cm处所对应的质量标度为多少克?()
小明按照此方法计算并标注了浮力秤各刻度值对应的质量标度。
(4)【任务三】拓展分析
小羽参照小明的方法,用一个横截面为圆形,切口处圆的面积也为50cm2,但上下粗细不同的饮料瓶来制作浮力秤。她正确标记了零刻度线的位置,用刻度尺紧贴瓶身,在瓶身上标注了均匀的刻度,如图丙所示;接着她依照小明浮力秤的刻度值,在相同的刻度处标注了相同的质量标度(图中未画出)。
请判断小羽制作的浮力秤所称出的物体质量比真实值偏大还是偏小?说明理由。
42.(2025·天津市)在跨学科实践活动中,同学们制作了如图所示的“浮力秤”,用来称量物体的质量。圆柱形薄壁外筒足够高且内装足量的水,带有秤盘的圆柱形浮体竖直漂浮在水中,浮体浸入水中的深度为 。已知浮体横截面积为S0,外筒横截面积为3S0,水的密度为ρ0。
(1)浮体和秤盘的总质量为 ;
(2)秤盘中未放物体,在水面位于浮体的位置标为“0”刻度线;秤盘中放质量为m1的砝码,在水面位于浮体的位置标为“m1”刻度线。请推导出这两条刻度线间的距离△h的表达式 ;
(3)为了测算该“浮力秤”的最大测量值,先把带有秤盘的浮体直立在外筒底部(图),再向外筒内缓慢注水,外筒底部受到水的压强与注入水质量的关系如图所示。当外筒底部受到水的压强至少为p1时,此“浮力秤”能够达到最大测量值,该最大测量值为 。
答案解析部分
1.C
AB、图中,悬浮时,物体的密度等于液体的密度,小球3此时悬浮,对应的温度为25℃,小球2漂浮,当温度继续升高为27℃时,液体密度减小,小球2将下沉,直至悬浮,小球2漂浮和悬浮时,受到的浮力等于小球2的重力,浮力不变,AB错误;
C、图中,小球4、5沉底,小球3悬浮,此时的温度在23℃~25℃间,C正确;
D、若增大所测量的最高温度,则液体密度更小,悬浮的小球的密度更小,需要增加体积相同,比小球1的密度更小的球,D错误。
故选C。
悬浮和漂浮时,物体受到的浮力等于物体的重力;悬浮物体的密度等于液体的密度;液体在温度升高时,密度减小;温度升高时,液体密度减小,悬浮的物体密度减小。
2.C
ABC、根据浮沉条件知,1号沉底,其密度大于液体的密度,而2、3、4漂浮,密度都小于液体的密度,根据漂浮时浮力等于重力,F浮=ρ水gV排=G=ρgV;
漂浮时如果物体的浸入的体积占总体积的比例越大,物体的密度就越接近液体的密度,即密度越大,ρ2>ρ3>ρ4;密度关系ρ1>ρ2>ρ3>ρ4;
根据G=mg=ρVg,已知密度关系,但不知道体积关系,故无法比较重力大小,
图中2号接近悬浮,密度在1、2之间,所以该海水为二等海水;故AB错误,C正确;
D、图中1号沉底,改盛四等海水,液体的密度更小,因而还是沉底,故排开液体的体积不变,但液体密度变小,根据阿基米德原理知,浮力减小,故D错误。
故答案为:C。
由图乙可知4个浮子在海水中的浮沉情况,根据浮沉分析其密度与液体密度关系解答;根据G=mg=ρVg比较重力,根据浮子的浮沉确定密度等级;根据阿基米德原理分析①号“浮子”所受浮力。
3.D
向漂浮在水面上的碗中加水,碗浸入水的深度越来越大,排开液体的体积增大,由F浮=ρ水gV排可得,所受浮力变大,
碗浸没水中,排开水的体积变小,由F浮=ρ水gV排可得,所受浮力变小,由于 碗里水的质量是缓慢均匀增加的,应该是线性关系,所以浮力先增大,后减小,最后不变,故只有D图符合题意。
故选D。
分析出排开液体的体积的变化,根据阿基米德原理判断出沉底前的浮力变化;碗沉底后排开水的体积不变,根据阿基米德原理判断出受到浮力的变化。
4.A
A.根据阿基米德原理F浮=ρ液gV排,液体密度液不变,鸡蛋浸入水中的体积排越大,所受浮力越大,故A正确;
B.鸡蛋沉入水底静止时,处于平衡状态,但此时浮力小于重力,所以鸡蛋才会下沉到水底,故B错误;
C.给水加热,主要是通过热传递的方式增大水的内能,而不是做功,故C错误;
D.锅盖被水蒸气顶起的过程是内能转化为机械能,与内燃机的做功冲程能量转化相同;而内燃机的压缩冲程是机械能转化为内能,二者能量转化不同,故D错误。
故选A。
A.根据阿基米德原理F浮=ρ液gV排分析判断;
B.根据浮沉条件分析判断;
C.改变物体内能的方式有两种:做功和热传递,热传递过程是能量的转移过程,做功过程是能量的转化过程。
D.内燃机的做功冲程能量转化是将内能转化为机械能,内燃机的压缩冲程是机械能转化为内能。
5.C
三种标尺上相同距离的刻线间对应的物体质量变化分别为Δm1、Δm2和Δm3。
假设相同距离的刻线间的距离为Δh;
在水槽外壁,标注刻度,△V排=S容Δh=225cm2×Δh;
根据阿基米德原理和浮力等于重力,ΔG=Δmg=ΔF浮=ρ水gΔV排;
物体的质量变化等于排开水的质量变化,
则△m1=ρ水△V排=ρ水×225cm2×Δh;
②在塑料杯内壁,用杯子浸入水中的深度变化标注;△V排2=S杯Δh=85cm2×Δh;
则△m2=ρ水△V排2=ρ水×85cm2×Δh;
③在水槽外壁,用杯底所装指针离槽底的高度h3的变化标注,当塑料杯下行Δh时,液面会升高,且体积变化相等,即S杯Δh=(S容-S杯)L;
;
;
则△m3=ρ水△V排3=ρ水×136.6Δh;
则△m1>△m3>△m2。
故选C。
要比较质量,需要分析重力,根据浮力秤是漂浮,浮力等于重力,因而质量的变化等于重力的变化,也等于浮力的变化,假设刻度的距离,根据所给的底面积计算排开液体的变化,根据阿基米德原理比较液体的重力与质量。
6.B
A、两球相同,甲中漂浮,所以球的密度小于甲中液体密度,乙中悬浮,所以球的密度等于乙液体的密度,所以甲的密度大于乙,故A错误;
B、压强相同,根据F=Ps可知,液体对容器底部的压力相同,压力等于液体的重力,所以液体质量相同,故B正确;
C、甲乙液体的质量相同,小球质量相同,所以总质量相同,对地面的受力面积相同,根据F=Ps可知,压强相同,故C错误;
D、甲乙漂浮和悬浮,重力等于浮力,重力相同,所以浮力相同,故D错误。
综上选B。
1、浮力的本质为上下表面产生的压力差,计算公式为F浮=ρ液gV排,所以物体所受浮力和物体所处的深度无关,与排开水的体积有关,当排开水的体积越小时,浮力越小,排开水的体积越大时,浮力越大
2、阿基米德原理:物体排开水的重力等于物体所受浮力;
3、物体沉浮条件:物体悬浮时的浮力等于重力(排开水的体积等于物体体积),物体的密度等于液体的密度,物体漂浮表明浮力等于重力(排开水的体积小于物体体积),物体的密度小于液体的密度,物体下沉时重力大于浮力(排开水的体积等于物体体积),物体的密度大于液体的密度;
4、压强的计算:公式为P=ρgh,压强和液体的密度、浸没深度有关,且密度越大,压强越大,深度越大,压强越大, 在同种液体的同一深度,液体向各个方向的压强 相同。
7.D
A.鞭炮爆炸内能转化为机械能,与内燃机做功冲程(内能转化为机械能)的能量转化方式相同,故A正确不合题意;
B.力可改变物体的形状,也可改变物体的运动状态,舞龙狮时力改变了物体的运动状态,故B正确不合题意;
C.庙会上各种小吃香气四溢是一种扩散现象,说明分子永不停息地做无规则运动,故C正确不合题意;
D.汤圆漂浮在水面上时受到的浮力等于重力,故D错误符合题意。
故选D。
A.内燃机做功冲程也将内能转化为机械能;
B.力可改变物体的形状,也可改变物体的运动状态;
C.扩散现象说明分子永不停息地做无规则运动;
D.根据物体的漂浮条件分析。
8.D
A.由题意,控制棒受到了重力、浮力和拉力的作用。当水位达到最高水位时,此时力传感器所受的拉力为F2,方向向下,根据力的作用是相互的,控制棒受到的拉力F2',大小等于F2,方向向上。此时控制棒排开水的体积为最大,浮力最大。控制棒的重力、浮力和拉力三个力的关系是:F浮+F2'=G=mg,可知F浮=mg-F2'=mg-F2,由F浮=ρ液gV排得:控制棒此时排开水的体积,故A错误。
B.当水位到达最低水位时,力传感器受到的拉力等于F1,方向向下,根据力的作用是相互的,控制棒受到的拉力F1',大小等于F1,方向向上。此时控制棒排开水的体积为最小,浮力最小。控制棒的重力、浮力和拉力三个力的关系是:F浮min+F1=G=mg,得F浮min=mg-F1,
由以上分析知:最高水位时浮力最大,F浮max=mg-F2,
则浮力的最大变化量ΔF浮max=(mg-F2)-(mg-F1)=F1-F2,故B错误;
C.由题意,最低水位时传感器的拉力为F1,此时控制棒对传感器的拉力最大,水泵启动进水。最高水位时传感器的拉力为F2,此时控制棒对传感器的拉力最小,水泵停止向水箱注水。故注水过程中,拉力逐渐从F1减小到F2。若进水过程中同时用水,相同时间内进水量大于出水量,所以此时水位是上升的,拉力是从F1减小到F2。若水泵停止注水(拉力已达到F2),开始用水,水位下降,则拉力从F2逐渐增大,直到水泵启动(此时拉力为F1)则不管是进水还是出水,拉力确实处于F1和F2之间,故C错误;
D.缩短悬挂控制棒的细线,因F1和F2触发的条件不变,控制棒的重力不变,由F浮=G-F知:则控制棒受到的浮力不变。
根据F浮=ρ液gV排得:,
若初始时细线的长度为L,控制棒的长度为h,水箱底到力传感器的距离为H。控制棒浸入水中的体积为V排,
设浸入深度为d,控制棒的横截面积为S棒,
则V排=S棒d,则,
因mg、F1、ρ水、S棒均不变,所以d不变;
则水位高度y=H-L-h+d,
缩短细线长度L,水位高度y变大,故D正确。
故选D。
物体受到了重力、浮力和拉力的作用,根据平衡力的知识分析这三个力的关系,再结合阿基米德原理进行分析。
9.D
A.图中甲悬浮,浮力等于重力,对甲充气,甲上浮变为漂浮,浮力还等于重力,甲的重力大于乙的重力,乙漂浮,浮力等于重力,再次静止时F甲大于F乙,故A错误;
B.对甲抽气,甲下沉,浮力小于自身重力,若抽出气体后,甲排开水的体积仍大于乙,由阿基米德原理可得,F甲还可以大于F乙,故B错误;
C.对乙充气,本来漂浮的,充气后仍漂浮,两次都是浮力等于重力,故乙再次静止时所受浮力与初始时的浮力相等,故C错误;
D.对乙抽气,如果仍漂浮或恰好悬浮,浮力还等于重力,乙再次静止时所受浮力可能等于初始时的浮力,故D正确。
故选D。
AB.根据漂浮和悬浮时浮力都等于重力分析;
CD.根据浮沉体积结合重力大小关系分析。
10.D
A、据图可知石头的质量为75g,添加水的质量为357g-(408g-75g)=24g,根据密度公式计算添加水的体积为,所以石头的体积为24cm3,根据密度公式计算石头的密度为,故A正确。
B、水和石头的总质量为408g,所以水的质量为408g-75g=333g,有步骤3可知,此时称的示数为332g,所以带出水的质量为333g-332g=1g,故B正确;
C、不计算带出水的质量,最终是将水加到标记处,计算是加水的差值,所以不会导致最终测量结果发生偏差,故C错误;
D、石头的重力G=mg=75×10-2N,石头的体积为24cm3,受到的浮力,所以支持力F=75N-24N=51N,故D错误。
1、浮力的本质为上下表面产生的压力差,计算公式为F浮=ρ液gV排,所以物体所受浮力和物体所处的深度无关,与排开水的体积有关,当排开水的体积越小时,浮力越小,排开水的体积越大时,浮力越大
2、利用水测量待测物体的密度:要保证水的体积和物体的体积相同,根据密度公式计算待测物体的密度。
11.小于;变小;变大
因为机翼上方的空气流速大,压强较小;机翼下方的空气流速小,压强大,这一压强差使飞机获得竖直向上的升力;由于机翼上方的压强小于下方压强,则机翼上方的压力小于飞机下方的压力。匀速飞行的“鲲龙”在投水灭火时,质量变小,速度不变,故动能变小。飞机漂浮在水面上,当遇险人员被救上“鲲龙”后,总重力变大,由物体的漂浮条件可知,飞机所受浮力的变大。
机翼的升力:机翼的上方是弧形,空气流过上方时流速大,压强小;机翼下方是平面,空气的流速小,压强大,这一压强差使飞机获得竖直向上的升力。动能的大小与质量和速度有关;飞机漂浮在水面上,当遇险人员被救上“鲲龙”后,总重力变大,由物体的漂浮条件可知飞机所受浮力的变化。
12.;变小
(1)根据阿基米德原理,浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开液体所受的重力,则该舰满载时所受浮力F浮=G排=m排g=4×107kg×10N/kg=4×108N。
(2)因为该舰在海水中始终处于漂浮状态,所以它受到的浮力始终等于自身重力。当舰由海水密度较小的近海驶向海水密度较大的远海区域时,浮力不变,根据F浮=ρ液gV排可知,ρ液增大,g不变,F浮不变,所以排开海水的体积V排将变小。
(1)由阿基米德原理可知,浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开液体所受的重力。
(2)根据F浮=ρ液gV排分析排开海水的体积变化即可。
13.0.5;0.6
因为木块漂浮在水面,受力平衡,则木块受到的浮力等于木块的重力:
F浮=G木=m木g=50×10-3kg×10N/kg=0.5N,
根据阿基米德原理可知,木块排开水的体积为:
;
木块的体积为:
;
木块的密度为:
。
故答案为:0.5;0.6。
(1)木块漂浮时,受到的浮力等于木块的重力,根据F浮=G=mg求出木块受到的浮力;
(2)根据阿基米德原理可求出木块排开水的体积和木块的体积,根据密度公式求出木块的密度。
14.0.8;1
实心球的质量,
实心球的体积,
若将实心球投入足够多的酒精中,实心球的密度大于酒精密度,故静止时,物体在酒精中沉底,
故此时所受浮力为:F浮'=ρ酒精gV=0.8×103kg/m3×10N/kg×1.0×10-4m3=0.8N;
实心球的密度小于盐水的密度,故在水中静止时,处于漂浮状态,则浮力等于重力,
故静止时物体受到的浮力为:F浮=G=1N。
知道物体的重力和密度,求得物体的质量和体积;
根据物体密度与酒精密度的关系判断出物体在酒精中的浮沉情况,根据阿基米德原理公式算出物体在酒精中的浮力;
将物体的密度和盐水的密度比较,根据物体的浮沉条件确定物体在盐水中的状态和受到的浮力。
15.先变大后不变;;58
据图可知,压力传感器的实数先变大后变小,物体对水的压力和水对物体的浮力属于相互作用力,所以浮力的变化为先变大后不变,据图可知,物体收到的浮力F=54N-34N=20N,物体的体积,密度为,剪短绳子后,采用整体发分析,水、物体、杯子的总重力m=34N+24N=58N,即压力传感器示数为58N。
1、浮力的本质为上下表面产生的压力差,计算公式为F浮=ρ液gV排,所以物体所受浮力和物体所处的深度无关,与排开水的体积有关,当排开水的体积越小时,浮力越小,排开水的体积越大时,浮力越大
2、根据密度公式计算m=ρv分析可知,体积相同是质量和密度成正比。
16.(1)多
(2)=;>
(3)方案一
(4)冰块熔化的快慢和接触面积有关;冰块熔化的快慢和液体密度有关
(5)不正确;向雪地撒盐,降低了雪的熔点,而冰在盐水中熔化,需要吸热,盐水的温度不一定比冰的熔点高,盐水中的冰不一定熔化快
探究影响冰块熔化快慢的因素时,
(1)冰熔化时,需要吸热,相同的冰放在不同液体中,熔化快慢不同,可知,在相同时间内,冰块熔化越快,则吸热越多;
(2)由于冰块相同,则重力相同,当冰在水中和盐水中漂浮时,根据二力平衡,受到的浮力等于冰的重力,则受到的浮力:F水=F盐水,根据F浮=ρ液gV排,盐水的密度比水的密度大,则排开盐水的体积比排开水的体积小,冰与盐水的接触面积比冰与水的接触面积小,则S水>S盐水;
(3)探究熔化快慢和接触面积的关系时,根据控制变量法,只改变接触面积,方案二中,冰块和液体的接触面积不同,但液体也不同,变量不唯一,方案一只改变了冰和水的接触面积,更合理;
(4)①利用方案一进行实验,当t2
(5)在雪地撒盐融雪,降低了雪的熔点,而冰在盐水中熔化,需要吸热,盐水的温度不一定比冰的熔点高,盐水中的冰不一定熔化快,可知预测冰块在浓盐水中熔化得更快是不正确的。
(1)固体熔化时,需要吸热,熔化越快,则吸收热量越多;
(2)相同的冰块重力相等,冰块漂浮时,受到的浮力等于重力,则在不同液体中漂浮,浮力相等;根据F浮=ρ液gV排,液体密度密度越大, 排开液体的体积越小,和液体的接触面积越小;
(3)探究冰熔化快慢和接触面积的关系,保持其他条件相同,只改变和液体的接触面积;
(4)在相同环境中,冰和液体的接触面积越大,熔化越快;在不同液体中,熔化快慢不同;
(5)雪地撒盐,可以降低雪的熔点,使雪更容易熔化,盐水的温度不一定高于冰的温度,盐水中的冰不一定熔化快。
17.(1)19.2;16;1.2
(2)1.0;0.5
(3)烧杯底部;不变
(1)根据步长约0.6m,通过马路共32步,计算路程为:s=0.6m×32=19.2m;根据图乙和丙,通过马路的时间为:t=16s,计算通过马路的速度约为:。
(2)图中,物体静止在水中,弹簧测力计的分度值为0.2N,根据指针位置, 拉力为1.0N,结合物体的重力,计算物体所受浮力的大小为:F浮=G-F拉=1.5N-1.0N=0.5N;
(3)探究水沸腾时温度变化规律时,图中,温度计的玻璃泡接触了烧杯底,是错误的:正确实验时,可得:水在沸腾时,持续吸热,温度保持不变。
(1)根据步行的步幅长度和步数,计算路程,结合秒表的指针位置,测量时间,根据,计算速度;
(2)根据测力计指针位置,测量拉力大小,利用物体的重力和浸没时的拉力差,计算浮力;
(3)使用温度将测量温度时,温度计的液泡不能碰到容器底或容器壁;液体沸腾时,吸收热量,温度保持不变。
18.(1)天平
(2)大;1.1
(3)小
(1)天平是测量物体质量的工具。
(2)根据可知,排水体积越大则浮力越大,土豆和水的总体积为600cm3,水的体积为400cm3,所以土豆的体积为200cm3,密度为。
(3)弹簧测力计示数F=G-F浮,土豆的密度越大,则G=ρ物gv排,所以物体的重力越大,,物体浸没在水中,浮力不变,,分析可知,密度越大, 则的值越 小。
1、天平的使用步骤:调零:天平置于水平台上,将游码归零,调节平衡螺母使得指针指向刻度中央,称重:是用镊子夹取砝码,测量时为左物右码,不断调整砝码和游码重量,使得天平重新平衡;测量为左物右码,量筒的使用:确定分度值,视线平行对准液面最低处,进行读数。
2、浮力:浮力产生的原因为上下表面存在压强差,根据阿基米德远离可知浮力的大小等于排开水的重力,浮力的公式F浮=ρ液gV排,应用:通过改变自身重力改变浮力,轮船以及潜水艇。
19.(1)漂浮;1.05
(2)
(3)5.5;0.96
(1)他们用铁钉插入粗细均匀、横截面积为0.2cm2的吸管并密封,制作了第一代密度计。使用铁钉的目的是使密度计重心降低、在液体中竖直漂浮。
测试时将其放入密度为1.0g/cm3的清水中,测得它的吃水深度为10.5cm;取出再放入盐水中,测得它的吃水深度为10.0cm,根据漂浮的特点浮力等于重力,可知两次受到的浮力相同,
由阿基米德原理有:ρ水gl1S=ρ盐gl2S;
即ρ水l1=ρ盐l2;
则盐水的密度为。
(2)因密度计漂浮,密度计在两种液体中受到液体对它的浮力相等,
由阿基米德原理有ρ水gh水S'=ρ盐gh盐S';
可推出这种粗细均匀的密度计在清水和盐水中的吃水深度的比值关系是;
(3)图中密度计下面的圆柱体的体积为V=S1h1=4.0cm2×5.0cm=20cm3=20×10-6m3=2×10-5m3;
故在水中排开水的体积为V水=2×10-5m3+(10.5-5.0)×0.2×10-6m3=2.11×10-5m3------①
设它在上述盐水中吃水深度为l,类似得出在盐水中排开液体的体积为
V盐=2×10-5m3+(l-5.0)×0.2×10-6m3------②
因密度计在两种液体中漂浮,故受到液体对它的 浮力都等于重力,故浮力相等,
由阿基米德原理有ρ水gV水=ρ盐gV盐------③
因 ------④
由①②③④得出:l=5.5cm;
若它在某种液体中的吃水深度为15.0cm,则排开这种液体的体积为
V液=2×10-5m3+(15.0-5.0)×0.2×10-6m3=2.2×10-5m3------⑤
根据阿基米德原理有ρ水gV水=ρ液gV液------⑥
由①⑤得:ρ液=0.96g/cm3
(1)密度计是根据漂浮的特点工作的;根据漂浮的特点浮力等于重力,可知两次受到的浮力相同,由阿基米德原理得出盐水的密度;
(2)因密度计漂浮,由漂浮的特点回答,由阿基米德原理可推出这种粗细均匀的密度计在清水和盐水中的吃水深度的比值关系;
(3)得出第三休密度计下面的圆柱体的体积,从而得出其在水中排开水的体积;设它在上述盐水中吃水深度为l,类似得出在盐水中排开液体的体积;因密度计在两种液体中受到的浮力相等,由阿基米德原理得出它在上述盐水中吃水深度;若它在某种液体中的吃水深度为15.0cm,得出排开这种液体的体积,根据阿基米德原理得出ρ液。
20.(1)体积
(2)2.7;0.5;无关;液体密度一定时,浮力的大小与物体浸在液体中的体积成正比
(3)体积;
(1)根据图中浸入的深度在改变,同时浸入的体积也改变,故浮力大小可能跟物体浸入液体的深度或物体浸在液体中的体积有关。
(2)①根据没有浸入液体时,弹簧测力计的示数等于重力为2.7N;
根据称重法计算浮力知,第2组实验中铝块受到的浮力F浮=G-F=2.7N-2.2N=0.5N;
②分析第1、3、4三组实验数据可知,浸入的深度改变,而拉力不变,说明浮力不变,故浮力大小跟物体浸入液体的深度无关;
③分析第1、2、3三组实验数据可得出初步结论:浸入的体积改变,拉力改变,浮力改变,深度变为2倍,浸入体积变为2倍,浮力分别是F浮=G-F=2.7N-2.2N=0.5N;
F'浮=G-F'=2.7N-1.7N=1N;
浮力变为了2倍,说明是正比关系,故说明液体密度一定时,浮力的大小与物体浸在液体中的体积成正比;
(3)利用浮力测液体密度时,根据浮力等于重力,相当于间接测量了液体的质量,因而控制体积相等;
根据浮沉条件知,增大浮力等于增大的液体的重力,G=F浮;
ρ水gV=1.0×103kg/m3×10N/kg×S×(0.11m-0.06m);
ρ液gV=1.0×103kg/m3×10N/kg×S×(0.12m-0.06m);
解得:ρ液=1.2ρ水=1.2×103kg/m3。
(1)根据图中浸入的体积不同分析;
(2)根据没有浸入液体时,弹簧测力计的示数等于重力,结合称重法计算浮力;
根据控制变量法分析数据得出结论;
(3)利用浮力测液体密度时,根据浮力等于重力,相当于间接测量了液体的质量,故需要控制体积不变;结合左侧数据分析。
21.(1)竖直
(2)0.4
(3)无关,由图丙和图丁可知,物体浸没在不同深度时,弹簧测力计示数不变,由称重法可知浮力不变,说明物体所受浮力的大小跟物体浸没的深度无关
(1)实验前,弹簧测力计要现在竖直方向调零,原因是弹簧测力计要测量重力,重力的方向竖直向下。
(2)根据称重法计算可知,乙图中的浮力F=1.4N-1.0N=0.4N;
(3)由乙丙丁分析可知随着浸没深度逐渐增加,其余因素不变化,弹簧测力计示数不变,所以浮力大小跟深度无关。
1、弹簧测力计:使用前弹簧测力计竖直调零,分度值为0.2N,重力方向竖直向下,据图读数,对钩码的拉力与弹簧测力计的弹簧轴线一致;
2、称重法测量物体浮力:先测出物体的重力,然后将物体浸入水中,弹簧测力计的示数就会减小,减小的示数就是物体受到的浮力;
3、浮力:浮力产生的原因为上下表面存在压强差,根据阿基米德远离可知浮力的大小等于排开水的重力,浮力的公式F浮=ρ液gV排,应用:通过改变自身重力改变浮力,轮船以及潜水艇。
22.(1)54;2.7×103
(2)变大;等于;
(1)据图可知,石头的质量为50g+4g=54g;密度为
(2)物块浸入水中的体积变大,根据浮力公式F=ρgv可知,浮力变大;据图可知,丁丙两图,物块的状态为漂浮,所以浮力等于重力,所以派开水的体积相同,容器的底面积相同,所以上升的高度相同,根据P=ρgh计算可知,丁的压强等于丙;圆柱的底面积为S,物体漂浮,所以重力等于浮力,石头的质量m=;由图丁可知,石头的体积,所以V石=S(h1-h2);所以密度为。
1、测量物体密度试验:原理为ρ=m/v,使用的仪器为天平和量筒;
天平的使用步骤:1、调零:天平置于水平台上,将游码归零,调节平衡螺母使得指针指向刻度中央,
称重:是用镊子夹取砝码,测量时为左物右码,不断调整砝码和游码重量,使得天平重新平衡;测量为左物右码;量筒的使用:确定分度值,视线平行对准液面最低处,进行读数。
2、阿基米德原理:物体排开水的重力等于物体所受浮力;
3、物体沉浮条件:物体悬浮时的浮力等于重力(排开水的体积等于物体体积),物体的密度等于液体的密度,物体漂浮表明浮力等于重力(排开水的体积小于物体体积),物体的密度小于液体的密度,物体下沉时重力大于浮力(排开水的体积等于物体体积),物体的密度大于液体的密度。
23.
假设容器的底面积为S,由图甲、乙可知,梨在水中受到的浮力:F浮=ρ水gV排=ρ水gS(h2-h1),
由图乙可知,梨漂浮在水面,根据物体的浮沉条件可知,梨的重力G=F浮=ρ水gS(h2-h1),
假设酱油的密度为ρ酱油,由图丙、丁可知,梨在酱油中受到的浮力:F'浮=ρ水gV'排=ρ酱油gS(h4-h3),
由图丁可知,梨漂浮在酱油中,根据物体的浮沉条件可知,F'浮=G,
即ρ酱油gS(h4-h3)=ρ水gS(h2-h1),
解得:酱油的密度:。
根据甲、乙两图,利用阿基米德原理求出梨在水中受到的浮力,根据物体的浮沉条件可知梨的重力;
由图丙、丁表示出梨在酱油中受到的浮力,根据物体的浮沉条件可知梨在水中和酱油中受到的浮力相等,据此解出酱油的密度。
24.(1)解: 合金块的重力为
(2)解: 合金块放入锥形瓶内浸没。排开水的体积与金属块的体积相等为
合金块放入锥形瓶内稳定后所受浮力为
(3)解: 图乙中合金块对锥形瓶底的压力为
合金块对锥形瓶底的压强为
(4)解: 合金块放入锥形瓶前后,液面上升的高度为
水对锥形瓶底的压强变化为
水对锥形瓶底的压力变化量为
(1)已知正方体合金块的质量,根据G=mg求合金块的重力;
(2)已知正方体合金块的边长,根据V=L3求合金块的体积,合金浸没在水中,排开水的体积等于它的体积,根据F浮=ρ液gV排求合金块放入锥形瓶内稳定后所受浮力大小;
(3)根据力的平衡条件求瓶底对合金块的支持力,根据力的相互性可知合金块对瓶底的压力,根据求合金块对锥形瓶底的压强;
(4)合金块放入锥形瓶后,根据V=Sh求水面高度的变化量,根据p=P液gh求水对瓶底的压强变化 量,根据求水对锥形瓶底的压力变化量。
25.(1)解: 容器底部受到的压强
(2)解: A处于漂浮状态,A受到的浮力
由得A排开水的体积
A漂浮时浸入水中的深度
(3)解: A、B悬浮时,受到总浮力
B受到的重力
B开始运动时,A上表面与B下表面重合,距容器底距离
A、B刚好浸没时,液面上升的高度
B刚好浸没时,下表面距容器底的距离
B开始运动到刚好浸没时运动的距离
B的重力做功
(1)根据p=ρ液gh求容器底部受到水的压强;
(2)根据物体的漂浮条件求出A漂浮时受到的浮力,根据F浮=ρ液gV排求出此时A排开水的体积,根据V=Sh求出此时A浸入水中的深度;
(3)当AB悬浮时,将二者的体积相加得到排开水的总体积,然后根据阿基米德原理计算此时它们受到的浮力,接下来减去A的重力计算出B的重力。
B开始运动时,A上表面与B下表面重合, 计算出距离容器底部的距离和液面上升的高度。再计算出B刚好浸没时下表面到容器底部的距离,进而计算出B从开始运动到刚好浸没通过的距离,最后根据W=Gh计算B的重力做功即可。
26.(1)解: 质量为18kg的水的重力
(2)解: 由图像乙可知,当A容器中注水4kg时,水对A容器底的压强为1×103Pa,此时A容器中水的深度
此时A容器中水的体积
A容器的底面积
由图像乙可知,当注入水的质量为4~6kg时,水对A容器底部的压强不变,说明A容器此时水面到达细管位置,水流入B容器,当B容器水面到达细管位置时,注入B容器中水的质量
当B容器中注入水的质量为2kg时,即
此时B容器中水的深度与A容器中水的深度相同,则B容器的底面积为A容器底面积的一半,即
当往整个装置中注入水的质量为5kg时,注入B容器中水的质量
此时B容器中水的体积
此时B容器中水的深度
水对B容器底部的压强
(3)解: 冰球放入A容器后水面刚稳定时B容器中水的深度增加了0.03m,则A容器中水的深度增加了0.03m,则冰球浸入水中的体积
冰球处于漂浮状态,则所受浮力等于重力,则冰球的重力
冰球的质量
冰球的总体积
冰的体积
冰球内部气泡的总体积
(1)根据重力公式G=mg计算18kg水的重力;
(2)当注水4kg,此时水对A的容器为103Pa,根据P=ρgh计算A容器的深度h;根据密度公式计算水的体积,A容器底面积,据图可知当注入水的质量为4~6kg时,水对A容器底部的压强不变,说明A容器此时水面到达细管位置,注入B容器中水的质量,当B容器中注入水的质量为2kg时,即,且B容器中水的深度与A容器中水的深度相同,所以,当往整个装置中注入水的质量为5kg时,注入B容器中水的质量,根据密度公式计算B容器中水的体积,B容器中水的深度,根据压强公式计算水对B容器底部的压强。
(3) 冰球放入A容器后水面刚稳定时B容器中水的深度增加了0.03m,所以A容器中水的深度增加了0.03m,则冰球浸入水中的体积,此时冰球处于漂浮状态,则冰球的重力,根据重力公式计算冰球质量,冰球的总体积,结合密度公式计算冰的体积,所以冰球内部气泡的总体积。
27.(1)解:
(2)解:
(3)解:
(1) 长方体空鱼缸的重力G为64N , 鱼缸与桌面接触面积S为0.16cm2, 根据F=Ps计算 空鱼缸对水平桌面的压强。
(2) 鱼缸中注入h为0.2m深的水 ,根据P=ρgh计算 放入假山石前,水对鱼缸底的压强。
(3) 假山石的体积V石为,水的密度,根据浮力公式计算计算 浸没在水中的假山石受到的浮力 。
28.(1)解: 空塑料瓶的重力为
由于漂浮,空载时塑料瓶受到的浮力为。
(2)解: 当塑料瓶满载时,浸入水中深度最大,此时塑料瓶排开水的体积为;
此时塑料瓶受到的浮力为
此时所载物体的重力为;
浮力称的最大称量值为。
(3)解: 浮力秤空载时和最大称量时塑料瓶浸入水中的体积变化量为
水槽内水面高度差为。
(1)空载时塑料瓶受到的浮力等于塑料瓶的重力,使用公式F浮=G计算;
(2)先根据求出瓶身最大排水体积,然后根据阿基米德原理F浮=ρ水gV排求出最大浮力,然后根据平衡力的知识计算所载物体的重力,再根据计算出最大称量质量;
(3)先求出浮力秤空载时和最大称量时塑料瓶浸入水中的体积变化量,再用体积变化量除以水槽底面积即可得到结果。
29.(1)解: 根据阿基米德原理,浸在液体中的物体受到向上的浮力,浮力的大小等于物体排开液体所受的重力,即
由图乙可知,小桶的重力
当时,排开水的重力
所以正方体E受到的浮力
(2)解: 由图乙可知,正方体E从刚接触水面到刚好完全浸没所用的时间
正方体E完全浸没时排开水的重力
根据,可得正方体E的体积
所以正方体E的边长
升降台匀速上升的速度
(3)解: 当 时,正方体 E 已经完全浸没在水中,此时力传感器 A 的示数 。由前面计算可知
如果正方体 E 的密度大于水:根据称重法可得正方体 E 的重力
正方体 E 的质量
正方体 E 的密度
如果正方体 E 的密度小于水:根据称重法可得正方体 E 的重力
正方体 E 的质量
正方体 E 的密度
故正方体 E 的密度为 或
(1)由图乙可知,小桶的重力,根据平衡力的知识计算排开水的重力,根据阿基米德原理可求得正方体E受到的浮力;
(2)由图乙可知,正方体E从刚接触水面到刚好完全浸没所用的时间和正方体E完全浸没时排开水的重力,由F浮=ρ液gV排可求得正方体排开水的体积,即为正方体的体积,然后可求得正方体E的边长,由速度公式可求得升降台匀速上升的速度;
(3)当t=10s时,正方体E已经完全浸没在水中,此时力传感器A的示数FA=2N,
分两种情况讨论:如果正方体E的密度大于水,根据称重法可得正方体E的重力G=F浮总+FA,然后可求正方体E的质量,由密度公式可求正方体E的密度:
如果正方体E的密度小于水,根据称重法可得正方体E的重力:G'=F浮总-FA,同理可求得正方体E的密度。
30.(1)解: 由题意可知工件的质量为90kg,则工件的重力为:
答:工件的质量为900N。
(2)解: 工件一半浸入清洗液时,进入深度为为:
则底部受到压强为:
答:清洗液对工件底部的压强为2000Pa。
(3)解: 工件完全浸入清洗液,工件受到的浮力为:
则工件的体积:
工件的底面积为:
答:工件的底面积为0.05m2。
(4)解: 刚好浸没时
液面上升的高度为:
工件下降的高度为:
工件从接触液面到刚好完全浸入所用的时间为 :
设池底部压强为p,经过时间为t,则有
则
代入数据解得
池底部压强为,
答:若工件以1.5cm/s的速度浸入清洗液,则工件从接触液面到刚好完全浸入所用的时间为25s,清洗液对清洗池底部的压强随时间变化的关系式是p=4800+40t,0≤t≤25。
(1)已知工件的质量,根据G=mg求工件的重力;
(2)由工件的高度可知工件一半浸入清洗液时,工件底部的深度,根据P=ρgh求出工件底部受到的压强;
(3)已知工件的重力和绳对工件的拉力,根据求出工件受到的浮力;工件完全浸入清洗液,根据求出工件的体积;已知工件的高度,根据求出工件的底面积;
(4)根据V=Sh得到工件刚好浸没,液面上升的高度,工件下降的高度为浸入的深度和液面上升的高度之差,根据速度变形公式得到时间;
设池底压强为p,经过的时间为t,根据V=Sh得到排开液体的体积的关系,得到升高的高度和时间的关系,根据液体压强的公式得到池底压强的关系。
31.(1)解:将物块A放置于玻璃容器底部中央,物块A对容器底部的压力为
则物块A对容器底部的压强
(2)解:当水深为时,水对容器底部的压强
注入水的体积为
(3)解:质量为的水体积为
A的体积为
容器的容积为
B的密度为
则B漂浮时受到的浮力为
则B漂浮时排开水的体积为
B漂浮时浸入水中的深度为
因为
所以最终B漂浮;因为
所以水没有溢出,则最终水深为
则B上升的高度为
则水对物块B所做的功
(1)A的质量为1kg,根据重力公式计算其重力G=mg,结合压强公式计算物块A对容器底部的压强。
(2)根据P=ρgh计算水深为时,水对容器底部的压强;
(3)根据密度公式计算质量为的水体积,B的密度;A的体积为,容器的容积为,分析可知B的密度小于水的密度,所以B漂浮,受到浮力等于重力,即;
则B漂浮时排开水的体积为,B漂浮时浸入水中的深度为,据此分析B最终的浮沉状态。以及水最终是否溢出和最终水深,所以B上升的高度为,根据计算水对物块B所做的功。
32.(1)解: 物体C的重力
(2)解: 当物体C完全浸没时,由图可知杆对物体C的压力为
对C受力分析,C受到重力、浮力和压力,则
则物体C完全浸没时排开水的体积
(3)解: 当物体C的下端刚好露出水面时,水舱模型内剩余水的体积
C的下端距离水舱模型底部的距离
当力传感器示数为时
①若杆对物体C的压力为
对C受力分析,C受到重力、浮力和压力,则
物体C排开水的体积
物体C浸在水中的深度
此时水的深度为
则水对水舱模型底部的压强
②若杆对物体C的拉力为
对C受力分析,C受到重力、浮力和拉力,则
解得
物体C排开水的体积
物体C浸在水中的深度
此时水的深度为
则水对水舱模型底部的压强
所以当力传感器示数为2N时,水对水舱模型底部的压强为或。
(1) 物体C是质量,根据G=mg计算其重力;
(2)当物体C完全浸没时,杆对物体C的压力为,对其进行受力分析可知;结合浮力公式计算C完全浸没时排开水的体积;
(3) 当物体C的下端刚好露出水面时,水舱模型内剩余水的体积为;所以C的下端距离水舱模型底部的距离,当力传感器示数为时,分2种情况进行考虑:
①若杆对物体C的压力为,对C受力分析,则;物体C排开水的体积;物体C浸在水中的深度;此时水的深度为;根据压强公式计算水对水舱模型底部的压强。
②若杆对物体C的拉力为,对C受力分析,;物体C排开水的体积;物体C浸在水中的深度,此时水的深度为;根据压强公式P=ρgh计算水对水舱模型底部的压强。
33.(1)解: 由阿基米德原理可知,“雪龙”号满载时受到的浮力
(2)解: 水面下5m深处船壁受到海水的压强
(3)解: “雪龙”号做匀速直线运动的速度为
由和得
则“雪龙”号主机提供的动力
(1)考察船漂浮,所以重力等于浮力,即;
(2)根据压强公式P=ρgh计算 水面下5m深处船壁受到海水的压强 ;
(3)“雪龙”号做匀速直线运动的速度为v;由和得,所以“雪龙”号主机提供的动力。
34.(1)解: 浮筒A的质量0.3kg,g取10N/kg,浮筒A的重力
(2)解: 当水位最低1.4m时,两端电压达到4V,因为与串联,电源电压恒为6V,
所以两端电压;
电路电流为;
则。
(3)解: 当到达最高水位1.6m时,设浮筒A上升距离为h,根据图乙可知此时弹簧拉力为
当浮筒A受到的浮力为
则有
即
解得:
浮筒A底部受到水的压强
当水位上升到最高1.6m时,两端电压达到2V,因为与串联,电源电压恒为6V,所以两端电压
电路电流为
则
即滑片上升0.15m,阻值增加了
因为电阻丝阻值与接入电路中的长度成正比,则接入电路中的总长度为
(4)解: 由(3)可知,水位高度H 时有
解得:
当水位高度为H 时,电路总电阻为
电路中电流其中()
(1)根据G=mg求出浮筒A的重力;
(2)由图甲可知两电阻串联;由题意可知当水位降到最低1.4m时R1两端电压为4V,根据串联电路的电压特点和欧姆定律求出此时R2的阻值;
(3)由题意可知当水位升高到1.6m时R1两端电压为2V,根据串联电路的电压特点和欧姆定律求出此时R2的阻值,进而求出水位由1.4m升高到1.6m时,R2接入电路的电阻变化量;
根据图乙表示出弹簧拉力大小与伸长量Δx的关系,根据力的平衡条件表示出水位达到1.6m时A的重力与A受到的浮力和拉力之间的关系,结合F浮=ρ液gV排和V=Sh求出此时弹簧伸长量的变化值,进而求出此时浮筒A底部到水面的深度,根据p=ρgh求出浮筒A底部受到水的压强;根据水位从1.4m升高到1.6m时R2接入电路的电阻变化量和电阻丝长度的变化量求出R2阻值与接入电路中的长度关系,进一步求出此时R2接入电路中的总长度;
(4)根据力的平衡条件表示出水位为H时A的重力与A受到的浮力和拉力之间的关系,结合F浮=ρ液gV排和V=Sh表示出此时弹簧的伸长量,进而表示出R2接入电路的电阻,根据串联电路的电阻特点和欧姆定律表示出水位高度在1.4m到1.6m时,电路中电流I与水位高度H的函数关系式。
35.(1)解: 航海器漂浮在水面上,根据浮沉条件可知浮力与重力大小相等,即
排开水的体积为
(2)解: 卸掉重2×105N的设备,航海器剩下的重力为
由图丙可知航海器底部到水面的最大距离为,此时排开水的体积最大;上方三棱柱浸在水中的深度为
即CG=3m,如上图所示,作AB边上的高CD,△ABC中,AB=8m,AC=BC,△ABC为等腰三角形,等腰三角形底边上的高为底边的中线,则AD=BD=4m,则△CDB为等腰三角形,则CD=4m,△ABC与△ECF相似,根据三角形相似有,即
则,上方三棱柱排开水的体积为
代入数据得,清掉泥沙,下方三棱柱排开水的体积为,航海器所受最大浮力为
浮力小于重力,所以搁浅位置24小时内,航海器不能浮起来。
(1) 航海器漂浮在水面上,此时重力等于浮力,根据浮力公式计算排开水的体积;
(2)卸掉重2×105N的设备,据此计算航海器剩下的重力为,知航海器底部到水面的最大距离为,据此计算上方三棱柱浸在水中的深度h,据图分析结合相似三角形可知
,据此求解,上方三棱柱排开水的体积为,求解排开水的体积V,清掉泥沙,下方三棱柱排开水的体积为,根据浮力公式P=ρgV排航海器所受最大浮力,分析和重力的大小关系,分析是否能漂浮。
36.(1)钢的质量:
答: 钢的质量为790kg;
(2)根据阿基米德原理可得,轮船满载时所受的浮力:
答: 轮船满载时所受的浮力为
(3)解:轮船底部受到的海水压强:
根据 可得,轮船底部受到的压力:
答: 轮船底部受到的压力为
(1)根据m=ρv计算钢的质量;
(2)船只漂浮,所以重力等于浮力,即轮船满载时所受的浮力: ;
(3)根据P=ρgh计算轮船底部受到的海水压强,根据 计算轮船底部受到的压力。
37.(1)解: 航行的距离:
答:如果汽车用7.2km/h速度在水中航行30min,它航行的距离为3.6×103m;
(2)解: 车底受到水的压强:
答:当汽车在水中航行时,若车的底部距水面0.8m,车底受到水的压强为8×103Pa;
(3)解: 汽车在水中满载航行时受到的浮力:
答: 汽车在水中满载航行时受到的浮力为4×104N。
(1)根据s=vt计算汽车航行的距离;
(2)利用P=ρgh计算车底受到水的压强;
(3根据阿基米德原理F浮=G排=m排g计算受到的浮力。
38.(1)解: 该船受到的总重力:
答:该船受到的总重力为4.12×107N;
(2)解: 船只漂浮,静止时,受到浮力为:
则排开海水的体积:
答:静止时排开海水的体积为4×103m3;
(3)解: 发动机完全燃烧100kg燃油放出的热量:
答:发动机完全燃烧100kg燃油放出的热量为4.3×109J。
(1)已知船的总质量,根据G=mg求该船受到的总重力;
(2)船静止时,漂浮在海面上,根据二力平衡条件F浮=G可知船所受的浮力大小,根据阿基米德原理F浮=ρ液gV排求出该船静止时排开海水的体积;
(3)已知燃油的质量,根据Q放=mq计算发动机完全燃烧100kg燃油放出的热量。
39.(1)解: 当容器内水的深度为,容器底所受压强
(2)解: 当容器内水的深度时,杯子排开水的体积
根据阿基米德原理,杯子此时所受的浮力
此时杯子对容器底部的压力刚好为零,即
杯子的质量
(3)解: 由题意可知:杯中水的重力等于增加的浮力,即,由此可得
代入数据
解得,杯子中水的体积
当杯口与容器内的水面相平时,杯子排开水的体积
组成杯子的材料的体积
杯子材料的密度
(4)解: 杯子注满水后,杯子的总重力
杯子对容器底的压力
注满水时杯子对容器底部的压强
解法二:
继续向杯子中注水直至注满,此时杯子浸没于水中,即,注满水时杯子对容器底部的压强
(1)已知深度,根据压强p=ρ液gh计算;
(2)根据漂浮的条件结合阿基米德原理计算杯子的质量;
(3)根据两次都是压力为0,结合增大的水的重力等于浮力,结合阿基米德原理计算杯子的体积,根据密度公式计算;
(4)根据注满水计算总重力,结合压力等于重力减去浮力,根据压强公式计算。
40.(1)空载
(2)解: 在水深5000m处海水对钻头的压强
(3)解: 井架对甲板的压力。
井架对甲板的压强
(4)解: 当装载货物时,根据阿基米德原理,货物重力
则货物排开液体
,当船吃水深度为时,船浸在水中船头梯形的面积
船浸入水中的体积
船空载时排开水的体积
空载时,船浸在水中船头的梯形的面积
空载时,船浸在水中的梯形的面积
解得,只要船在空载时能通过大桥,就能始终确保安全通行,旗杆的最大高度
(1)题目中提到“梦想”号钻探船上有高耸的井架,出海执行任务时需要通过大桥。为了确保安全通行,我们需要考虑船只在最不利情况下的高度。船空载时,船的整体重力小,排开液体体积小,吃水深度浅,船露出水面高;满载时,整体重力大,排开液体体积大,吃水深度深,船露出水面低;所以只要空载时能通过大桥,就能始终确保安全通行
(1)为了确保安全通行,我们需要考虑船只在最不利情况下的高度;
(2)根据p=ρgh求出深度为5000m处海水的压强;
(3)根据G=mg算出井架的重力,井架对甲板的压力等于自身的重力,根据压强公式计算井架对甲板的压强;
(4)先计算装载货物时排开液体的体积,根据θ=45°算出船浸入水中的体积,进而算出空载体积和高度,旗杆的最大高度等于桥离水面的高度减去空载的高度。
41.(1)等于
(2)增加重物质量
(3)浮力秤的刻度转换基于阿基米德原理
增加质量m时,需额外排开水的体积
由平衡条件可知
化简得。
(4)小羽的饮料瓶上下粗细不同非圆柱形,但刻度均匀标注。实际浸入深度与排开水的体积不成线性关系,若瓶身向上渐扩,相同刻度下实际排开水的体积大于计算的圆柱形瓶的体积,真实值大于测量值,故制作的浮力秤所称出的物体质量比真实值偏小。
(1)瓶体呈竖直状态,且与重物整体漂浮,根据物体漂浮的条件可知,此时秤体所受浮力大小等于其重力大小;
(2)图甲中秤体在水中的位置尚未满足标记刻度的条件,说明称体排开水的体积较小,说明称体所受的浮力较小,由于称体与重物整体漂浮,根据F浮=ρgV排=G总可知,可以增加重物的质量,即增大物体的重力来增大称体所受的浮力,使称体排开水的体积增大,达到标记刻度的条件,故调整建议为:增加重物质量。
(3)浮力秤的刻度转换基于阿基米德原理
增加质量m时,需额外排开水的体积
由平衡条件可知
化简得
(4)小羽的饮料瓶上下粗细不同非圆柱形,但刻度均匀标注。实际浸入深度与排开水的体积不成线性关系,若瓶身向上渐扩,相同刻度下实际排开水的体积大于计算的圆柱形瓶的体积,真实值大于测量值,故制作的浮力秤所称出的物体质量比真实值偏小。
(1)物体处于漂浮状态,根据浮沉条件可知,浮力等于重力;
(2)图甲中重物的质量小,秤体浸入水中过浅,可以增加重物的质量使秤体浸入深度增加;
(3)根据阿基米德原理和漂浮条件计算瓶身上刻度1cm处所对应的质量标度;
(4)根据实际排开水的体积和计算式中排开水的差异判断。
42.(1)
(2)
(3)
(1)如图,带有秤盘的圆柱形浮体竖直漂浮在水中,浮体浸入水中的深度为h0,
则浮体和秤盘的总重力为G0=F浮0=ρ0gV排0=ρ0gS0h0;
则浮体和秤盘的总质量为;
(2)浮力秤始终漂浮,浮力等于重力,则ΔF浮=ΔG;
则有ΔG=m1g=ρ0gS0Δh,
解得:;
(3)从浮力秤恰好漂浮到外筒底部受到水的压强为p1时,
加入的水的重力为ΔG水=ΔF=ΔpS=(p1-ρ0gh0)×3S0;
则称量的物体质量最大时,浮力秤深度变化量为
;
结合(2)中解析式则有;
解得:最大测量值。
(1)根据漂浮时浮力等于重力,结合阿基米德原理计算;
(2)根据漂浮时,增大的浮力等于增大的重力,结合阿基米德原理列方程计算;
(3)根据压强和底面积计算压力,根据质量最大时,结合浮沉条件与阿基米德原理计算浮力秤深度的变化,结合深度与质量的关系计算。
21世纪教育网(www.21cnjy.com)
同课章节目录
