2026年中考数学复习课件 专题三 函数--第13讲 构建一次函数和反比例函数模型解决实际问题 (共50张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题三 函数--第13讲 构建一次函数和反比例函数模型解决实际问题 (共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 07:40:27 | ||
图片预览










文档简介
(共50张PPT)
复习讲义
第一篇 考点精讲
专题三 函数
第13讲 构建一次函数和反比例函数模型解决实际问题
聚焦核心
1.利用一次函数和反比例函数解决实际问题,关键是将实际问题转
化为数学问题,根据题目中变量之间的关系建立一次函数和反比例函数
模型,充分运用一次函数和反比例函数的图象和性质解题.注意要根据
实际问题的意义确定自变量的取值范围.
2.建立一次函数和反比例函数模型解决实际问题的一般步骤:
(1)审题,根据题意列出(求出)函数解析式(一般利用待定系
数法求函数解析式);
(2)根据已知条件和实际问题的意义确定自变量的取值范围;
(3)结合函数的图象和性质解题;
(4)结合实际问题的意义,检验自变量取值范围的合理性.
第13讲 构建一次函数和反比例函数模型解决实际问题
案例分析
考点一 构建一次函数模型解决实际问题
名师指导
1.当题目中给出了实际问题中两个变量满足的图象是直线(线段、射线),或两个变量满足的关系式形如
2.实际问题中一次函数的最大(小)值:对于一次函数
,当时,有最小值 ,最大值
;当时,有最大值,最小值 .
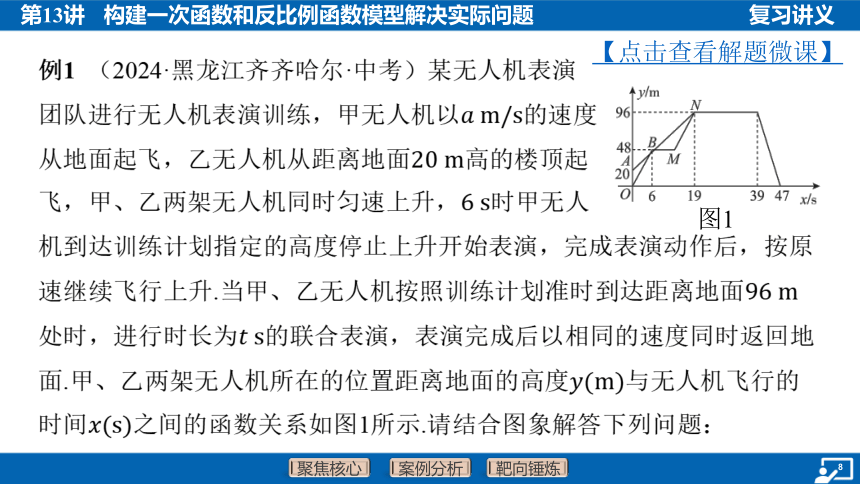
图1
例1 (2024·黑龙江齐齐哈尔·中考)某无人机表演
团队进行无人机表演训练,甲无人机以 的速度
从地面起飞,乙无人机从距离地面 高的楼顶起
飞,甲、乙两架无人机同时匀速上升, 时甲无人
机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原
速继续飞行上升.当甲、乙无人机按照训练计划准时到达距离地面
处时,进行时长为 的联合表演,表演完成后以相同的速度同时返回地
面.甲、乙两架无人机所在的位置距离地面的高度 与无人机飞行的
时间 之间的函数关系如图1所示.请结合图象解答下列问题:
【点击查看解题微课】
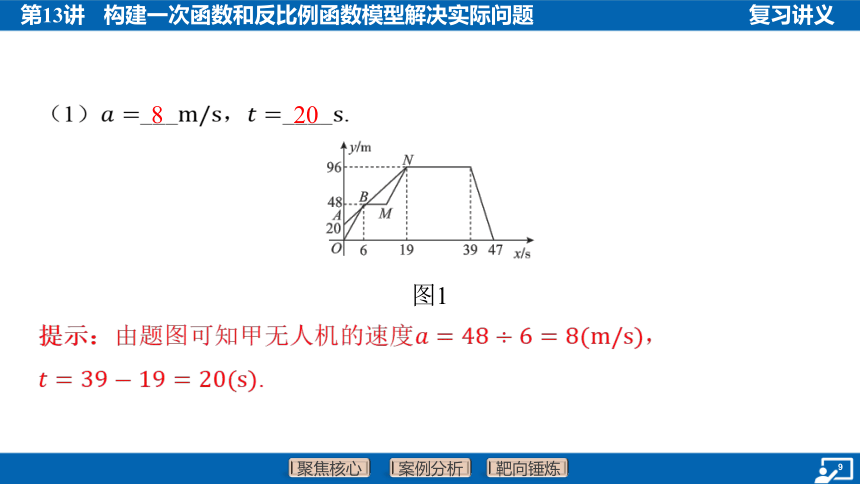
(1)___,____ .
8
20
图1
提示:由题图可知甲无人机的速度 ,
.
图1
(2)求线段 所在直线对应的函数解析式.
解:因为甲无人机的速度为 ,甲无人机匀速从0到所用时间为 ,所以甲无人机单独表演所用时间为.
从而得点 的横坐标为.
所以.
设线段 所在直线对应的函数解析式为 ,将
,代入,得 解得
所以线段 所在直线对应的函数解析式为 .
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为 ?
(直接写出答案即可)
图1
提示:由图象可知,,易得线段
所在直线对应的函数解析式为,线段 所在
直线对应的函数解析式为,线段 所
在直线对应的函数解析式为 .设两架无人机表
演训练到时,它们距离地面的高度差为 .结合图象可知,当
时,,解得或 (舍去).当
时,,解得或 (舍去). 当
时,,解得.
图1
【答案】两架无人机表演训练到或或 时,它们距离地面的高度差为 .
图1
思路点拨(1)根据图象得到关于高度和时间的信息,
从而可求得和 的值.
(2)已知点的坐标和点 的纵坐标,则需结合题
意和图象分析,求出点 的横坐标,即可运用待定
系数法求出线段 所在直线对应的函数解析式.
(3)先求出各时间段甲、乙两架无人机所在的位置距离地面的高度
关于无人机飞行的时间的函数解析式,再由高度差为 列方
程求解.注意,需根据时间段分类讨论.
考点专练
1.跨学科题(2025·山西朔州·模拟)如图2,在测量液体密度的实验中,
小明根据测得的液体和烧杯的总质量与液体的体积 ,绘制
了如图3所示的函数图象(图中为一条线段),则当 时,
_____ .
212
图2
图3
2.(2024·山东济南·中考节选)近年来,光伏建筑一体化广受关注.某社
区拟修建A,B两种光伏车棚.已知修建一个A种光伏车棚需投资3万元,
修建一个B种光伏车棚需投资2万元.修建A,B两种光伏车棚共20个,要
求修建的A种光伏车棚的数量不少于修建的B种光伏车棚数量的2倍,问
修建多少个A种光伏车棚时,投资总额最少?最少投资总额为多少万元?
解:设修建A种光伏车棚个,则修建B种光伏车棚 个.
根据题意,得.
解得.
设修建A,B两种光伏车棚共投资 万元,则,即.由,得随 的增大而增大.
又,且为正整数,所以当时, 取得最小值,最小值为 .
答:修建14个A种光伏车棚时,投资总额最少,最少投资总额为54万元.
考点二 构建反比例函数模型解决实际问题
名师指导
1.在运用反比例函数解决实际问题时,要先确定问题中的哪两个变
量成反比例关系,根据题设中的描述建立反比例函数模型,再运用反比
例函数的性质解决实际问题,如求解特定值、最大值或最小值等.要注
意自变量的取值必须符合实际意义.
2.在实际问题中,当两个变量的乘积为一个定值时,这两个变量成
反比例关系,即可设出形如的解析式,再根据待定系数法求出 的
值.与物理学有关的反比例函数模型,通常有以下几种: ,
,,,, ,等等.
例2 跨学科题(2025·河南·模拟改编)小明在课余时间找了几副度数不
同的近视眼镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光
斑最小.此时他测量了镜片到光斑的距离,得到的数据如下表:
… 400 625 800 …
… 0.25 0.16 0.125 0.10 …
图4
为了进一步研究镜片度数 与镜片到光斑的
距离 之间的关系,小明借助计算机绘制了表示
变量间关系的图象(如图4).
图4
(1)求与之间的函数解析式及 的值.
解:由题图得,镜片度数与镜片到光斑的距离 之间成反比例函数关系,设,将(0.25,400) 代入,得.
故.
将 代入,得 .
图4
(2)小亮的近视眼镜是500度,用小亮的眼镜做实
验,请写出镜片到光斑的距离,并进行解释说明.
(保留两位小数)
解:镜片到光斑的距离为 .
理由如下:当时,,解得 .
故镜片到光斑的距离为 .
图4
(3)根据图表中的信息,说明随着逐渐变大,
的变化趋势是什么.(直接写出结论)
解:根据图表中的信息,发现随着 逐渐变大, 的变化趋势是逐渐变小.
图4
(4)如果是一副平光镜(近视度数为0),那么会
不会有光斑存在?(直接写出结论,不需要解释).
提示:由反比例函数的图象和性质可知,当 趋近
于无穷大时, 趋近于0,但不会等于0,所以当
时,光斑不会存在.
【答案】光斑不会存在.
思路点拨 由图象可知镜片度数与镜片到光斑的距离 之间成反比例函
数关系,利用待定系数法求出反比例函数的解析式,再根据反比例函数
的性质解答问题.
图4
考点专练
3.跨学科题 【阅读与思考】
下面是小明同学的一篇数学日记,请仔细阅读并完成相应的任务.
在数学活动课上,我们数学兴趣小组的同学参加了一次“探索压力
一定时,压强与受力面积 之间的函数关系的数学活动”.
图5
第一步,如图5,将一长方体 放置于一水平玻璃桌
面上,按不同的方式摆放,计算并记录受力面积
与桌面所受压强 .
第二步,数据整理,记录的数据如下:
图5
第一组 第二组 第三组 第四组 第五组 第六组
0.1 0.15 0.2 0.25 0.3 0.4
600 400 300 25 200 150
第三步,数据分析,以的数值为横坐标, 的数值为纵坐标建立平
面直角坐标系,在该坐标系中描出以表中数对为坐标的各点,并用光滑
的曲线顺次连接这些点.
图5
在数据分析过程中,我发现一组数据可能有错误,重新进行实验,
证明了我的猜想正确,并对数据进行了修改,实验结束后,大家有很多
收获,每人都撰写了数学日记.
【任务】
图5
(1)你认为表中第____组数据是错误的;并直接
写出关于 的函数解析式:_______.
四
提示:设,将代入,得 .所以
.将第二、三、五、六组数据代入,均满足此
式子.故关于的函数解析式为 .
第一组 第二组 第三组 第四组 第五组 第六组
0.1 0.15 0.2 0.25 0.3 0.4
600 400 300 25 200 150
(2)在图6的平面直角坐标系中,画出此函数的图象.
图6
解:画出函数图象如图13.
图13
图5
(3)结合图象,如果要求压强不超过 ,那
么长方体的受力面积至少为____ .
0.6
图6
第13讲 构建一次函数和反比例函数模型解决实际问题
靶向锤炼
靶向练
1.(2024·河北·中考)节能环保已成为人们的共识.淇淇家计划购买
电,若平均每天用电,则能使用 天.下列说法错误的
是( ).
C
A.若,则 B.若,则
C.若减小,则也减小 D.若减小一半,则 增大一倍
图1
2.(2024·贵州·中考)五一国际劳动节期间,小星一
家驾车前往黄果树景点旅游,在行驶过程中,汽车
离黄果树景点的路程与所用时间 之间的函
数关系如图1所示,下列说法正确的是( ).
D
A.小星家离黄果树景点的路程为
B.小星从家出发内的平均速度为
C.小星从家出发离景点的路程为
D.小星从家到黄果树景点共用了
图2
3.(2024·湖北武汉·模拟)在一次体育课上进行跳绳测试,小明跳绳的平均成绩为每分钟100个,小强跳绳的平均成绩为每分钟150个,小明先跳150个,然后小强跳,图2是小明、小强跳绳的个数 关于小强的跳绳时间 的函数图象,这两个函数图象的交点 的纵坐标是_______.
提示:根据题意可得,小明跳绳的个数与 的函数解析式为,小强跳绳的个数与 的函数解析式为.解 得
450
4.(2024·山东青岛·中考)为培养学生的创新意识,提高学生的动手能
力,某校计划购买一批航空、航海模型.已知商场某品牌航空模型的单
价比航海模型的单价多35元,用2 000元购买航空模型的数量是用1 800
元购买航海模型数量的 .
(1)求航空和航海模型的单价.
解:设航空模型的单价为元,则航海模型的单价为 元.
根据题意,得.解得.
经检验, 是原分式方程的解,且符合题意.
则 .
答:航空模型的单价为125元,航海模型的单价为90元.
(2)学校采购时恰逢该商场六一儿童节促销:购买航空模型打八折.已
知购买航空、航海模型共120个,且航空模型数量不少于航海模型数量
的 ,请问分别购买多少个航空和航海模型,学校花费最少?
解:设购买航空模型个,购买航空和航海模型的总费用为 元,则购买航海模型 个.
根据题意,得.
由,可知 随 增大而增大.
因为,所以.
故当时, 有最小值,最小值为,则 .
答:当购买航空模型40个,购买航海模型80个时,学校花费最少.
攻坚练
5.(2025·河南漯河·模拟)综合与实践
【提出问题】
如何称量一个空矿泉水瓶的质量?
图3
【知识背景】
图3是一架自制天平,支点 固
定不变,左侧托盘固定在点 处,
右侧托盘(点)可以在横梁 段
滑动(点不与点,重合).已知, ,
左侧托盘中砝码的质量为 .根据杠杆原理,平衡时,左盘砝码质量
右盘物体质量 (不计托盘与横梁质量).
【分析问题】
图3
(1)设右侧托盘中放置物体的质量
为,的长为,求 关于
的函数解析式,并求出自变量的取
值范围.
解:因为左盘砝码的质量为,,所以 ,即.
因为,, 所以.
由点 可以在横梁段滑动,得,即 .
【解决问题】
图3
(2)由于一个空的矿泉水瓶太轻无
法称量,称量时进行如下操作:左
侧托盘放置 的砝码,右侧托盘
(点)由点向点 滑动,向空瓶
中加入的水后,发现点移动到的长为 时天平平衡.求这个
空矿泉水瓶的质量.
解:设空矿泉水瓶的质量为 .
根据题意,得1 .
.
答:这个空矿泉水瓶的质量为 .
图3
拔尖练
6.(2025·江西赣州·模拟)图4为某新款茶吧机,开机加热时每分钟上升
,加热到时停止加热,水温开始下降,此时水温 与通
电时间成反比例关系.当水温降至 时,饮水机再自动加热.
若水温在时接通电源,水温与通电时间 之间的关系如图5所示,
则下列说法中错误的是( ).
图4
图5
A.水温从加热到,需要
B.水温下降过程中,与的函数解析式是
C.上午10点接通电源,可以保证当天10:30能喝到不低于 的水
D.在一个加热与降温的周期内水温不低于的时间为
图4
图5
提示:水温从加热到,所需时间为 ,故选项
A说法正确.设水温下降过程中,与的函数解析式为,将
代入,得.解得.所以水温下降过程中,与 的函数解析
式是.故选项B说法正确.令,则.所以 .所以
从开机加热到水温降至需要,即一个循环为 .设加热
过程中水温与通电时间的函数解析式为 ,将
代入,得.解得.所以当 时,
.上午10点到10:30共,,所以当
时,,即此时的水温为 .故选项C说法正确.在
加热过程中,水温为时,,解得 .在水温下降
过程中,水温为时,,解得.因为 ,所以
一个加热与降温的周期内水温不低于的时间为 .故选项D说法
错误.
图4
图5
【答案】D
7.(2025·浙江衢州·中考改编)
视力表中蕴含着很多数学知识,如:每个“ ”形图都是正方形结构,
同一行的“ ”是全等图形且对应着同一个视力值,不同的检测距离需要
不同的视力表.
图6
【素材1】 国际通用的视力表以 为检测距离,任选视力表中7个视力值 ,测得对应行的“ ”形图的边长 ,在平面直角坐标系中描点如图6所示.
【探究1】
图6
(1)检测距离为时,归纳与 的关系式,并求视力值1.2所对应行的“ ”形图的边长.
解:由图象中点的坐标规律可得与 成反比例关系,设,将 代入,得0.
解得.所以 .
将其余各点一一代入验证,都符合此关系式.
将代入,得 .
所以视力值1.2所对应行的“ ” 形图的边长为 .
图7
【素材2】 图7为视网膜成像示
意图,在检测视力时,眼睛能看清最
小“ ”形图所成的角叫作分辨视角.
视力值与分辨视角 (分)的对应关系近似满足 .
【探究2】
图7
(2)当 时,属于正常视力,
请根据函数的性质写出对应的分辨视
角 的取值范围.
解:由可知,在自变量 的取值范围内,随 的增大而减小.
所以当时,.又,所以 .
复习讲义
第一篇 考点精讲
专题三 函数
第13讲 构建一次函数和反比例函数模型解决实际问题
聚焦核心
1.利用一次函数和反比例函数解决实际问题,关键是将实际问题转
化为数学问题,根据题目中变量之间的关系建立一次函数和反比例函数
模型,充分运用一次函数和反比例函数的图象和性质解题.注意要根据
实际问题的意义确定自变量的取值范围.
2.建立一次函数和反比例函数模型解决实际问题的一般步骤:
(1)审题,根据题意列出(求出)函数解析式(一般利用待定系
数法求函数解析式);
(2)根据已知条件和实际问题的意义确定自变量的取值范围;
(3)结合函数的图象和性质解题;
(4)结合实际问题的意义,检验自变量取值范围的合理性.
第13讲 构建一次函数和反比例函数模型解决实际问题
案例分析
考点一 构建一次函数模型解决实际问题
名师指导
1.当题目中给出了实际问题中两个变量满足的图象是直线(线段、射线),或两个变量满足的关系式形如
2.实际问题中一次函数的最大(小)值:对于一次函数
,当时,有最小值 ,最大值
;当时,有最大值,最小值 .
图1
例1 (2024·黑龙江齐齐哈尔·中考)某无人机表演
团队进行无人机表演训练,甲无人机以 的速度
从地面起飞,乙无人机从距离地面 高的楼顶起
飞,甲、乙两架无人机同时匀速上升, 时甲无人
机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原
速继续飞行上升.当甲、乙无人机按照训练计划准时到达距离地面
处时,进行时长为 的联合表演,表演完成后以相同的速度同时返回地
面.甲、乙两架无人机所在的位置距离地面的高度 与无人机飞行的
时间 之间的函数关系如图1所示.请结合图象解答下列问题:
【点击查看解题微课】
(1)___,____ .
8
20
图1
提示:由题图可知甲无人机的速度 ,
.
图1
(2)求线段 所在直线对应的函数解析式.
解:因为甲无人机的速度为 ,甲无人机匀速从0到所用时间为 ,所以甲无人机单独表演所用时间为.
从而得点 的横坐标为.
所以.
设线段 所在直线对应的函数解析式为 ,将
,代入,得 解得
所以线段 所在直线对应的函数解析式为 .
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为 ?
(直接写出答案即可)
图1
提示:由图象可知,,易得线段
所在直线对应的函数解析式为,线段 所在
直线对应的函数解析式为,线段 所
在直线对应的函数解析式为 .设两架无人机表
演训练到时,它们距离地面的高度差为 .结合图象可知,当
时,,解得或 (舍去).当
时,,解得或 (舍去). 当
时,,解得.
图1
【答案】两架无人机表演训练到或或 时,它们距离地面的高度差为 .
图1
思路点拨(1)根据图象得到关于高度和时间的信息,
从而可求得和 的值.
(2)已知点的坐标和点 的纵坐标,则需结合题
意和图象分析,求出点 的横坐标,即可运用待定
系数法求出线段 所在直线对应的函数解析式.
(3)先求出各时间段甲、乙两架无人机所在的位置距离地面的高度
关于无人机飞行的时间的函数解析式,再由高度差为 列方
程求解.注意,需根据时间段分类讨论.
考点专练
1.跨学科题(2025·山西朔州·模拟)如图2,在测量液体密度的实验中,
小明根据测得的液体和烧杯的总质量与液体的体积 ,绘制
了如图3所示的函数图象(图中为一条线段),则当 时,
_____ .
212
图2
图3
2.(2024·山东济南·中考节选)近年来,光伏建筑一体化广受关注.某社
区拟修建A,B两种光伏车棚.已知修建一个A种光伏车棚需投资3万元,
修建一个B种光伏车棚需投资2万元.修建A,B两种光伏车棚共20个,要
求修建的A种光伏车棚的数量不少于修建的B种光伏车棚数量的2倍,问
修建多少个A种光伏车棚时,投资总额最少?最少投资总额为多少万元?
解:设修建A种光伏车棚个,则修建B种光伏车棚 个.
根据题意,得.
解得.
设修建A,B两种光伏车棚共投资 万元,则,即.由,得随 的增大而增大.
又,且为正整数,所以当时, 取得最小值,最小值为 .
答:修建14个A种光伏车棚时,投资总额最少,最少投资总额为54万元.
考点二 构建反比例函数模型解决实际问题
名师指导
1.在运用反比例函数解决实际问题时,要先确定问题中的哪两个变
量成反比例关系,根据题设中的描述建立反比例函数模型,再运用反比
例函数的性质解决实际问题,如求解特定值、最大值或最小值等.要注
意自变量的取值必须符合实际意义.
2.在实际问题中,当两个变量的乘积为一个定值时,这两个变量成
反比例关系,即可设出形如的解析式,再根据待定系数法求出 的
值.与物理学有关的反比例函数模型,通常有以下几种: ,
,,,, ,等等.
例2 跨学科题(2025·河南·模拟改编)小明在课余时间找了几副度数不
同的近视眼镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光
斑最小.此时他测量了镜片到光斑的距离,得到的数据如下表:
… 400 625 800 …
… 0.25 0.16 0.125 0.10 …
图4
为了进一步研究镜片度数 与镜片到光斑的
距离 之间的关系,小明借助计算机绘制了表示
变量间关系的图象(如图4).
图4
(1)求与之间的函数解析式及 的值.
解:由题图得,镜片度数与镜片到光斑的距离 之间成反比例函数关系,设,将(0.25,400) 代入,得.
故.
将 代入,得 .
图4
(2)小亮的近视眼镜是500度,用小亮的眼镜做实
验,请写出镜片到光斑的距离,并进行解释说明.
(保留两位小数)
解:镜片到光斑的距离为 .
理由如下:当时,,解得 .
故镜片到光斑的距离为 .
图4
(3)根据图表中的信息,说明随着逐渐变大,
的变化趋势是什么.(直接写出结论)
解:根据图表中的信息,发现随着 逐渐变大, 的变化趋势是逐渐变小.
图4
(4)如果是一副平光镜(近视度数为0),那么会
不会有光斑存在?(直接写出结论,不需要解释).
提示:由反比例函数的图象和性质可知,当 趋近
于无穷大时, 趋近于0,但不会等于0,所以当
时,光斑不会存在.
【答案】光斑不会存在.
思路点拨 由图象可知镜片度数与镜片到光斑的距离 之间成反比例函
数关系,利用待定系数法求出反比例函数的解析式,再根据反比例函数
的性质解答问题.
图4
考点专练
3.跨学科题 【阅读与思考】
下面是小明同学的一篇数学日记,请仔细阅读并完成相应的任务.
在数学活动课上,我们数学兴趣小组的同学参加了一次“探索压力
一定时,压强与受力面积 之间的函数关系的数学活动”.
图5
第一步,如图5,将一长方体 放置于一水平玻璃桌
面上,按不同的方式摆放,计算并记录受力面积
与桌面所受压强 .
第二步,数据整理,记录的数据如下:
图5
第一组 第二组 第三组 第四组 第五组 第六组
0.1 0.15 0.2 0.25 0.3 0.4
600 400 300 25 200 150
第三步,数据分析,以的数值为横坐标, 的数值为纵坐标建立平
面直角坐标系,在该坐标系中描出以表中数对为坐标的各点,并用光滑
的曲线顺次连接这些点.
图5
在数据分析过程中,我发现一组数据可能有错误,重新进行实验,
证明了我的猜想正确,并对数据进行了修改,实验结束后,大家有很多
收获,每人都撰写了数学日记.
【任务】
图5
(1)你认为表中第____组数据是错误的;并直接
写出关于 的函数解析式:_______.
四
提示:设,将代入,得 .所以
.将第二、三、五、六组数据代入,均满足此
式子.故关于的函数解析式为 .
第一组 第二组 第三组 第四组 第五组 第六组
0.1 0.15 0.2 0.25 0.3 0.4
600 400 300 25 200 150
(2)在图6的平面直角坐标系中,画出此函数的图象.
图6
解:画出函数图象如图13.
图13
图5
(3)结合图象,如果要求压强不超过 ,那
么长方体的受力面积至少为____ .
0.6
图6
第13讲 构建一次函数和反比例函数模型解决实际问题
靶向锤炼
靶向练
1.(2024·河北·中考)节能环保已成为人们的共识.淇淇家计划购买
电,若平均每天用电,则能使用 天.下列说法错误的
是( ).
C
A.若,则 B.若,则
C.若减小,则也减小 D.若减小一半,则 增大一倍
图1
2.(2024·贵州·中考)五一国际劳动节期间,小星一
家驾车前往黄果树景点旅游,在行驶过程中,汽车
离黄果树景点的路程与所用时间 之间的函
数关系如图1所示,下列说法正确的是( ).
D
A.小星家离黄果树景点的路程为
B.小星从家出发内的平均速度为
C.小星从家出发离景点的路程为
D.小星从家到黄果树景点共用了
图2
3.(2024·湖北武汉·模拟)在一次体育课上进行跳绳测试,小明跳绳的平均成绩为每分钟100个,小强跳绳的平均成绩为每分钟150个,小明先跳150个,然后小强跳,图2是小明、小强跳绳的个数 关于小强的跳绳时间 的函数图象,这两个函数图象的交点 的纵坐标是_______.
提示:根据题意可得,小明跳绳的个数与 的函数解析式为,小强跳绳的个数与 的函数解析式为.解 得
450
4.(2024·山东青岛·中考)为培养学生的创新意识,提高学生的动手能
力,某校计划购买一批航空、航海模型.已知商场某品牌航空模型的单
价比航海模型的单价多35元,用2 000元购买航空模型的数量是用1 800
元购买航海模型数量的 .
(1)求航空和航海模型的单价.
解:设航空模型的单价为元,则航海模型的单价为 元.
根据题意,得.解得.
经检验, 是原分式方程的解,且符合题意.
则 .
答:航空模型的单价为125元,航海模型的单价为90元.
(2)学校采购时恰逢该商场六一儿童节促销:购买航空模型打八折.已
知购买航空、航海模型共120个,且航空模型数量不少于航海模型数量
的 ,请问分别购买多少个航空和航海模型,学校花费最少?
解:设购买航空模型个,购买航空和航海模型的总费用为 元,则购买航海模型 个.
根据题意,得.
由,可知 随 增大而增大.
因为,所以.
故当时, 有最小值,最小值为,则 .
答:当购买航空模型40个,购买航海模型80个时,学校花费最少.
攻坚练
5.(2025·河南漯河·模拟)综合与实践
【提出问题】
如何称量一个空矿泉水瓶的质量?
图3
【知识背景】
图3是一架自制天平,支点 固
定不变,左侧托盘固定在点 处,
右侧托盘(点)可以在横梁 段
滑动(点不与点,重合).已知, ,
左侧托盘中砝码的质量为 .根据杠杆原理,平衡时,左盘砝码质量
右盘物体质量 (不计托盘与横梁质量).
【分析问题】
图3
(1)设右侧托盘中放置物体的质量
为,的长为,求 关于
的函数解析式,并求出自变量的取
值范围.
解:因为左盘砝码的质量为,,所以 ,即.
因为,, 所以.
由点 可以在横梁段滑动,得,即 .
【解决问题】
图3
(2)由于一个空的矿泉水瓶太轻无
法称量,称量时进行如下操作:左
侧托盘放置 的砝码,右侧托盘
(点)由点向点 滑动,向空瓶
中加入的水后,发现点移动到的长为 时天平平衡.求这个
空矿泉水瓶的质量.
解:设空矿泉水瓶的质量为 .
根据题意,得1 .
.
答:这个空矿泉水瓶的质量为 .
图3
拔尖练
6.(2025·江西赣州·模拟)图4为某新款茶吧机,开机加热时每分钟上升
,加热到时停止加热,水温开始下降,此时水温 与通
电时间成反比例关系.当水温降至 时,饮水机再自动加热.
若水温在时接通电源,水温与通电时间 之间的关系如图5所示,
则下列说法中错误的是( ).
图4
图5
A.水温从加热到,需要
B.水温下降过程中,与的函数解析式是
C.上午10点接通电源,可以保证当天10:30能喝到不低于 的水
D.在一个加热与降温的周期内水温不低于的时间为
图4
图5
提示:水温从加热到,所需时间为 ,故选项
A说法正确.设水温下降过程中,与的函数解析式为,将
代入,得.解得.所以水温下降过程中,与 的函数解析
式是.故选项B说法正确.令,则.所以 .所以
从开机加热到水温降至需要,即一个循环为 .设加热
过程中水温与通电时间的函数解析式为 ,将
代入,得.解得.所以当 时,
.上午10点到10:30共,,所以当
时,,即此时的水温为 .故选项C说法正确.在
加热过程中,水温为时,,解得 .在水温下降
过程中,水温为时,,解得.因为 ,所以
一个加热与降温的周期内水温不低于的时间为 .故选项D说法
错误.
图4
图5
【答案】D
7.(2025·浙江衢州·中考改编)
视力表中蕴含着很多数学知识,如:每个“ ”形图都是正方形结构,
同一行的“ ”是全等图形且对应着同一个视力值,不同的检测距离需要
不同的视力表.
图6
【素材1】 国际通用的视力表以 为检测距离,任选视力表中7个视力值 ,测得对应行的“ ”形图的边长 ,在平面直角坐标系中描点如图6所示.
【探究1】
图6
(1)检测距离为时,归纳与 的关系式,并求视力值1.2所对应行的“ ”形图的边长.
解:由图象中点的坐标规律可得与 成反比例关系,设,将 代入,得0.
解得.所以 .
将其余各点一一代入验证,都符合此关系式.
将代入,得 .
所以视力值1.2所对应行的“ ” 形图的边长为 .
图7
【素材2】 图7为视网膜成像示
意图,在检测视力时,眼睛能看清最
小“ ”形图所成的角叫作分辨视角.
视力值与分辨视角 (分)的对应关系近似满足 .
【探究2】
图7
(2)当 时,属于正常视力,
请根据函数的性质写出对应的分辨视
角 的取值范围.
解:由可知,在自变量 的取值范围内,随 的增大而减小.
所以当时,.又,所以 .
同课章节目录
