3.3垂径定理 教学设计 北师大版(2024)数学九年级下册
文档属性
| 名称 | 3.3垂径定理 教学设计 北师大版(2024)数学九年级下册 | 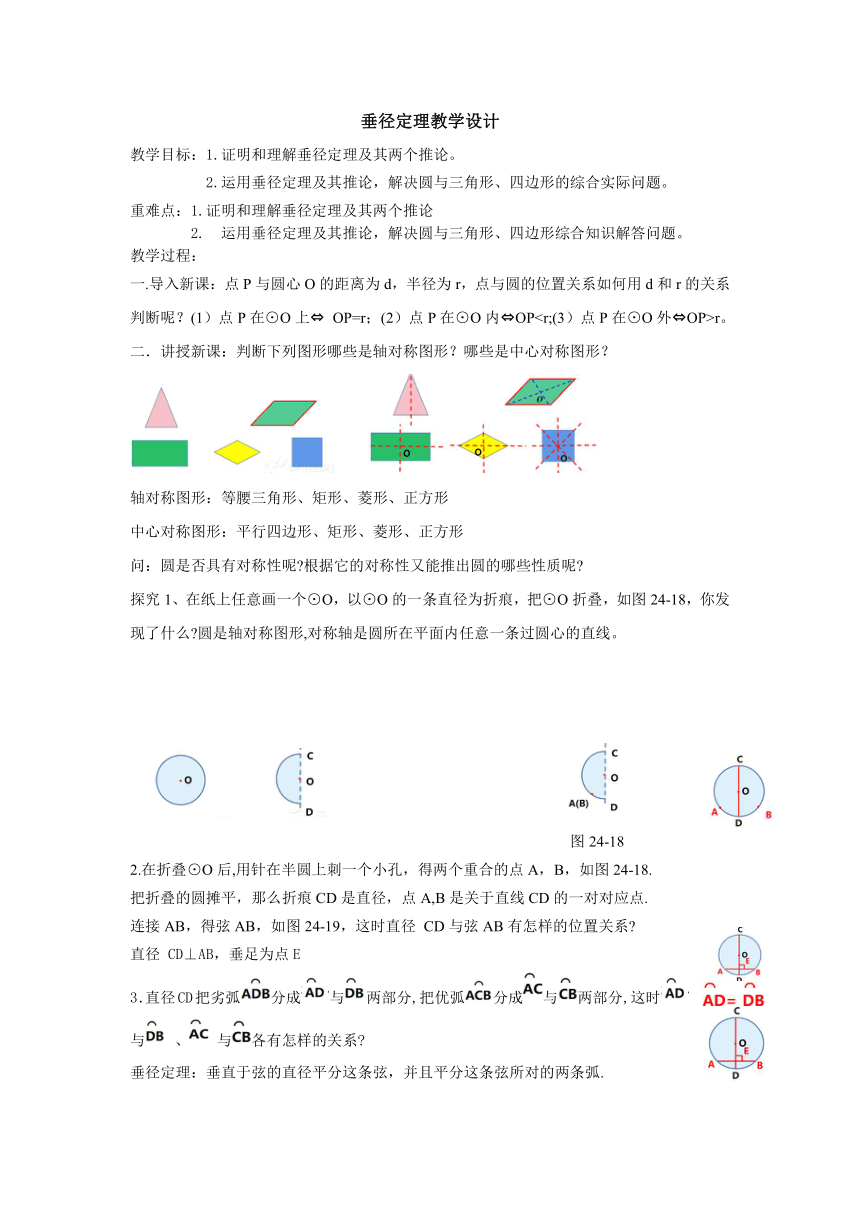 | |
| 格式 | docx | ||
| 文件大小 | 398.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 07:46:15 | ||
图片预览

文档简介
垂径定理教学设计
教学目标:1.证明和理解垂径定理及其两个推论。
2.运用垂径定理及其推论,解决圆与三角形、四边形的综合实际问题。
重难点:1.证明和理解垂径定理及其两个推论
运用垂径定理及其推论,解决圆与三角形、四边形综合知识解答问题。
教学过程:
一.导入新课:点P与圆心O的距离为d,半径为r,点与圆的位置关系如何用d和r的关系判断呢?(1)点P在⊙O上 OP=r;(2)点P在⊙O内 OPr。
二.讲授新课:判断下列图形哪些是轴对称图形?哪些是中心对称图形?
轴对称图形:等腰三角形、矩形、菱形、正方形
中心对称图形:平行四边形、矩形、菱形、正方形
问:圆是否具有对称性呢 根据它的对称性又能推出圆的哪些性质呢
探究1、在纸上任意画一个⊙O,以⊙O的一条直径为折痕,把⊙O折叠,如图24-18,你发现了什么 圆是轴对称图形,对称轴是圆所在平面内任意一条过圆心的直线。
图24-18
2.在折叠⊙O后,用针在半圆上刺一个小孔,得两个重合的点A,B,如图24-18.
把折叠的圆摊平,那么折痕CD是直径,点A,B是关于直线CD的一对对应点.
连接AB,得弦AB,如图24-19,这时直径 CD与弦AB有怎样的位置关系
直径 CD⊥AB,垂足为点E
3.直径CD把劣弧分成与两部分,把优弧分成与两部分,这时与 、 与各有怎样的关系
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
已知:如图24-20,在⊙O中,CD是直径,AB是弦,并且CD⊥AB,垂足为E.
求证: AE= EB,
定理 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其它三个结论。
三:知识应用:判断下列命题是否正确:
1、平分一条直径的弦必垂直于这条直径( × )
2、平分一条弧的直线垂直于这条弧所对的弦( × )
3、弦的垂线必经过这条弦所在圆的圆心( × )
4、在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心( √ )
例2、如图24-21,⊙O的半径为5cm,弦AB为6cm,求圆心O到弦AB的距离。
例3 赵州桥(图24-22)建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆孤形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m, 求赵州桥桥拱所在圆的半径(精确到0.1m)
四:课堂练习:1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则OE=( )
A. 8cm B. 5cm C. 3cm D. 2cm
2.京西某游乐园的摩天轮采用了国内首创的横梁结构,是市民周末休闲的好去处.如图,如果该摩天轮主视图的直径为88米,最高点A距地面100米,匀速运行一圈所需的时间是18分钟.但受周边建筑物影响,如果乘客与地面距离不低于34米时为最佳观景期,那么在摩天轮运行的一圈中最佳观景的时长为_____分钟。
3.筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)
五.课堂小结:垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其它三个结论
六.布置作业:
同步练习
七.板书设计:
课题:24.2.2 垂径定理
1.垂径定理及其推论
2.例2
例3
教学目标:1.证明和理解垂径定理及其两个推论。
2.运用垂径定理及其推论,解决圆与三角形、四边形的综合实际问题。
重难点:1.证明和理解垂径定理及其两个推论
运用垂径定理及其推论,解决圆与三角形、四边形综合知识解答问题。
教学过程:
一.导入新课:点P与圆心O的距离为d,半径为r,点与圆的位置关系如何用d和r的关系判断呢?(1)点P在⊙O上 OP=r;(2)点P在⊙O内 OP
二.讲授新课:判断下列图形哪些是轴对称图形?哪些是中心对称图形?
轴对称图形:等腰三角形、矩形、菱形、正方形
中心对称图形:平行四边形、矩形、菱形、正方形
问:圆是否具有对称性呢 根据它的对称性又能推出圆的哪些性质呢
探究1、在纸上任意画一个⊙O,以⊙O的一条直径为折痕,把⊙O折叠,如图24-18,你发现了什么 圆是轴对称图形,对称轴是圆所在平面内任意一条过圆心的直线。
图24-18
2.在折叠⊙O后,用针在半圆上刺一个小孔,得两个重合的点A,B,如图24-18.
把折叠的圆摊平,那么折痕CD是直径,点A,B是关于直线CD的一对对应点.
连接AB,得弦AB,如图24-19,这时直径 CD与弦AB有怎样的位置关系
直径 CD⊥AB,垂足为点E
3.直径CD把劣弧分成与两部分,把优弧分成与两部分,这时与 、 与各有怎样的关系
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
已知:如图24-20,在⊙O中,CD是直径,AB是弦,并且CD⊥AB,垂足为E.
求证: AE= EB,
定理 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其它三个结论。
三:知识应用:判断下列命题是否正确:
1、平分一条直径的弦必垂直于这条直径( × )
2、平分一条弧的直线垂直于这条弧所对的弦( × )
3、弦的垂线必经过这条弦所在圆的圆心( × )
4、在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心( √ )
例2、如图24-21,⊙O的半径为5cm,弦AB为6cm,求圆心O到弦AB的距离。
例3 赵州桥(图24-22)建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆孤形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m, 求赵州桥桥拱所在圆的半径(精确到0.1m)
四:课堂练习:1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则OE=( )
A. 8cm B. 5cm C. 3cm D. 2cm
2.京西某游乐园的摩天轮采用了国内首创的横梁结构,是市民周末休闲的好去处.如图,如果该摩天轮主视图的直径为88米,最高点A距地面100米,匀速运行一圈所需的时间是18分钟.但受周边建筑物影响,如果乘客与地面距离不低于34米时为最佳观景期,那么在摩天轮运行的一圈中最佳观景的时长为_____分钟。
3.筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)
五.课堂小结:垂径定理及其的推论:
(1) 过圆心 (2)垂直于弦 (3) 平分弦
(4)平分弦所对的劣弧 (5)平分弦所对的优弧
以上五个中只要符合两个条件,就能得到其它三个结论
六.布置作业:
同步练习
七.板书设计:
课题:24.2.2 垂径定理
1.垂径定理及其推论
2.例2
例3
