第一章《勾股定理》复习题---利用勾股定理解决折叠问题(含解析)八年级数学上册北师大版
文档属性
| 名称 | 第一章《勾股定理》复习题---利用勾股定理解决折叠问题(含解析)八年级数学上册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 11:48:26 | ||
图片预览



文档简介
第一章《勾股定理》复习题---利用勾股定理解决折叠问题
【题型1 长方形中折痕过对角线模型】
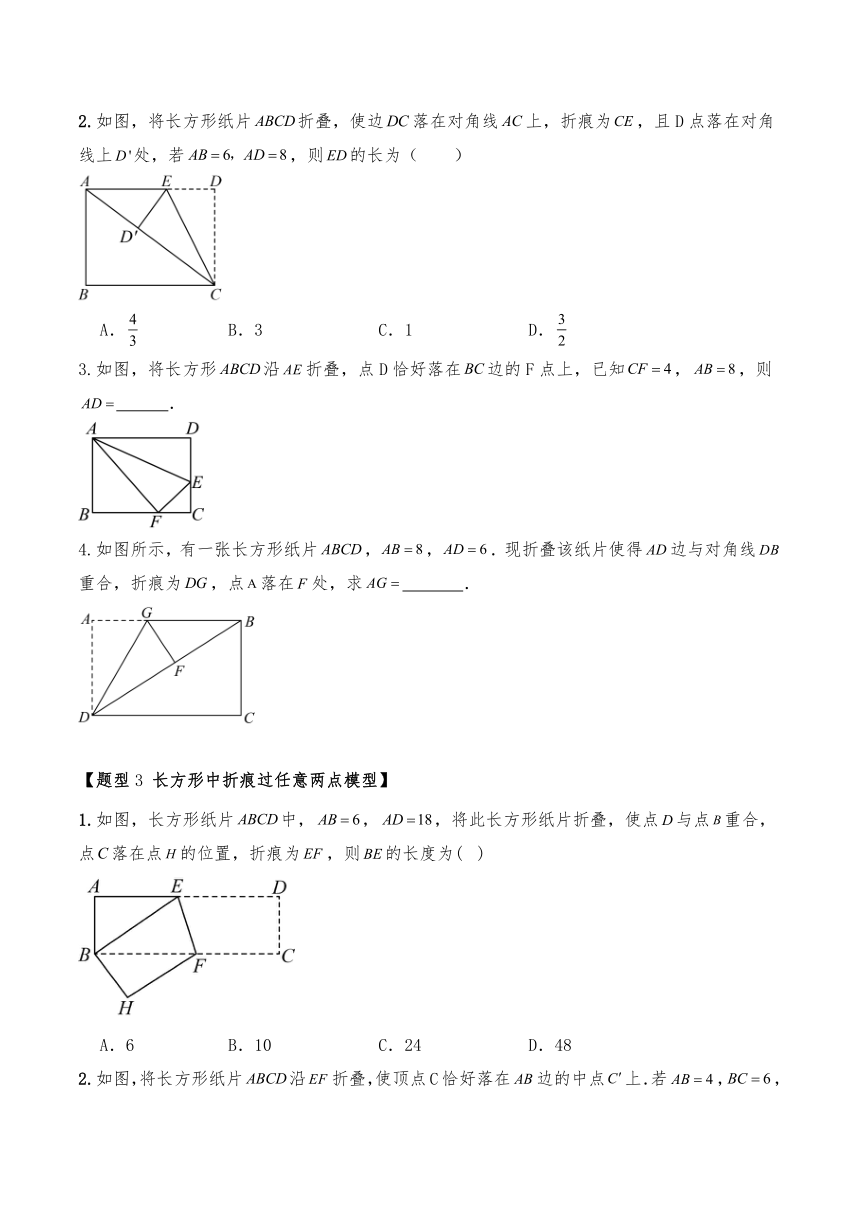
1.如图所示,把一张长方形纸片沿对角线折叠,若,求的长.
2.如图,在长方形ABCD中,,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于F,,则( )
A. B.3 C. D.6
3.如图,在长方形纸片中,,. 把长方形纸片沿直线折叠,点落在点处,交于点,则的长为( )
A. B. C. D.
4.如图,长方形ABCD中,,,如果将该长方形沿对角线BD折叠,使点C落在点F处,那么图中阴影部分的面积是______.
【题型2 长方形中折痕过一顶点模型】
1.如图,长方形纸片中,已知,折叠纸片使边与对角线重合,点B落在点F处,折痕为,且.
(1)求的长;
(2)求的长.
2.如图,将长方形纸片折叠,使边落在对角线上,折痕为,且D点落在对角线上处,若,则的长为( )
A. B.3 C.1 D.
3.如图,将长方形沿折叠,点D恰好落在边的F点上,已知,,则 .
4.如图所示,有一张长方形纸片,,.现折叠该纸片使得边与对角线重合,折痕为,点落在处,求 .
【题型3 长方形中折痕过任意两点模型】
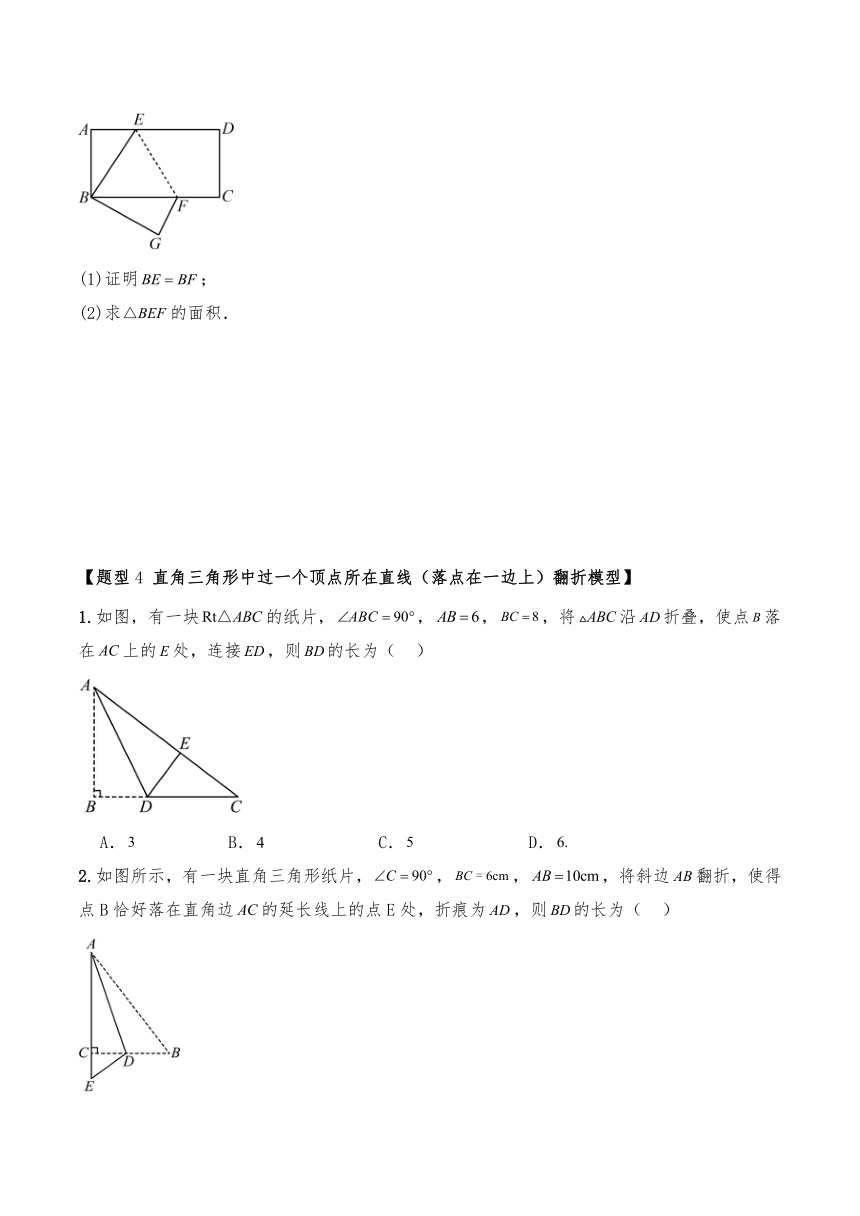
1.如图,长方形纸片中,,,将此长方形纸片折叠,使点与点重合,点落在点的位置,折痕为,则的长度为( )
A.6 B.10 C.24 D.48
2.如图,将长方形纸片沿折叠,使顶点C恰好落在边的中点上.若,,求的长.
3.已知,如图长方形中,,,将此长方形折叠,使点与点重合,折痕为,求的面积.
4.如图,长方形中,边,.将此长方形沿折叠,使点与点重合,点落在点处.
(1)证明;
(2)求的面积.
【题型4 直角三角形中过一个顶点所在直线(落点在一边上)翻折模型】
1.如图,有一块的纸片,,,,将沿折叠,使点落在上的处,连接,则的长为( )
A. B. C. D.
2.如图所示,有一块直角三角形纸片,,,,将斜边翻折,使得点B恰好落在直角边的延长线上的点E处,折痕为,则的长为( )
A. B. C. D.
3.如图,在等腰直角三角形中,,,点P是边上任意一点,连接,将沿翻折,点B的对应点为,当有一边与垂直时,的长为 .
4.如图是一张直角三角形纸片,,,.
(1)在图1中,将直角边沿折叠,使点落在斜边上的点处,求的长;
(2)在图2中,将沿折叠,使点与点重合,求的长.
【题型5 直角三角形中过斜边中点所在直线翻折模型】
1.如图,直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为.则的长是( )
A. B. C. D.
2.如图,在直角坐标系中,C点在线段上,D点在线段上,将沿直线折叠后,B点与A重合,则点C坐标是 .
3.如图,在中,,,.将按如图所示的方式折叠,使B,C两点重合,折痕为.求的长.
4.如图、为一块直角三角形纸片,.
【问题初探】:直角三角形纸片的对折问题,可以通过全等变换把所求线段转化成直角三角形的边,进而通过勾股定理来解决,体现数学中的转化思想.
(1)如图1,现将纸片沿直线折叠,使直角边落在斜边上,的对应点为,若,求的长.
【学以致用】
(2)如图2,若将直角沿折叠,点与中点重合,点分别在,上,则之间有怎样的数量关系?并证明你的结论.
【题型6 直角三角形中过任意两点所在直线(落在其中一边)翻折模型】
1.在中,,将沿直线折叠,使B落在的三等分点处,求的长.
2.如图,在中,,,.将折叠,使点落在的中点处,折痕为,则线段的长为( )
A. B. C.5 D.4
3.如图,在中,,,,将它的锐角翻折,使得点落在边的中点处,折痕交边于点,交边于点,则的长为( )
A.3 B.4 C. D.
4.在中,,,,分别是斜边和直角边上的点.把沿着直线折叠,顶点的对应点是点.
(1)如图1,若点和顶点重合,求的长;
(2)如图2,若点落在直角边的中点上,求的长.
参考答案
【题型1 长方形中折痕过对角线模型】
1.解:∵一张长方形纸片沿对角线折叠,
∴,
∴,
∴,
∴,
设,则,
在中,由勾股定理得
∴,
解得,
∴ .
2.A
【分析】根据折叠的性质,可知BF=DF=-EF,在Rt中,由勾股定理得:,由此即可求得EF值.
【详解】解:∵,,∴AD=,,
由折叠可知,AB=BE=6,AD=ED=,,,
∵,∴∠BDF=∠DBF∴BF=DF=-EF,
∴在Rt中,由勾股定理得:,
∴,解得:EF=,故选:A.
3.A
【分析】由已知条件可证△CFE≌△AFD,得到DF=EF,利用折叠知AE=AB=8cm,设AF=xcm,则DF=(8-x)cm,在Rt△AFD中,利用勾股定理即可求得x的值.
【解析】∵四边形ABCD是长方形,∴∠B=∠D=900,BC=AD,
由翻折得AE=AB=8m,∠E=∠B=900,CE=BC=AD
又∵∠CFE=∠AFD∴△CFE≌△AFD ∴EF=DF设AF=xcm,则DF=(8-x)cm
在Rt△AFD中,AF2=DF2+AD2,AD=6cm, 故选择A.
4.
【分析】要求阴影部分的面积就要先求得它的底和高,这个三角形的高就是,,由此关系就可利用勾股定理求出AE及EF的长,从而求三角形的面积.
【详解】解:四边形ABCD是矩形,,,,,
由折叠的性质,可得,,,,,
设,则,
,即,解得,.故答案为.
【题型2 长方形中折痕过一顶点模型】
1.(1)解:∵长方形纸片中,,折叠纸片使边与对角线重合,
∴,
∴,,
∴;
(2)∵折叠,
∴,
设,则:,
在中,,
∴,
∴,
∴.
2.B
【分析】本题考查矩形的折叠,勾股定理,熟练掌握运用勾股定理解决长方形的折叠是解题的关键.首先利用勾股定理计算出的长,再根据折叠可得,设,则,再根据勾股定理可得方程,再解方程即可.
【详解】∵,
∴,
∴根据勾股定理得,
根据折叠可得:,
∴,
设,则,
在中:,即,
解得:,
故答案为:B.
3.10
【分析】本题考查了折叠的性质、勾股定理,根据折叠的性质得出,设,则,根据勾股定理得出,求出,即可得出答案.
【详解】解:根据折叠的性质,,
长方形中,
设,则,
在中,由勾股定理得:,
即,
解得:,
∴,
故答案为:10.
4.3
【分析】本题考查了勾股定理与折叠问题;
先利用勾股定理求出,然后根据折叠的性质得到,,,求出,然后在中,利用勾股定理构建方程,即可求出.
【详解】解:∵,,,
∴,
由折叠得:,,,
∴,,
在中,,
∴,
∴,
故答案为:3.
【题型3 长方形中折痕过任意两点模型】
1.B
【分析】本题考查了勾股定理与折叠问题;由折叠可知,设利用勾股定理进行分析计算即可.
【详解】解:由折叠可知,
设
由勾股定理可得,
即,
解得,
,
故选:B.
2.解:由折叠的性质可得,
设,则,
∵是边的中点,
∴,
由长方形的性质可得,
在中,由勾股定理得,
∴,
解得,
∴.
3.解:过点作于点,
过点作于点,
四边形是长方形
四边形是矩形
设,
由折叠知,
,
在中,
解得,
,
,
又,
,
,
∴的面积为
4.(1)解:证明:四边形是长方形,
,,
将此长方形沿折叠,使点与点重合,点落在点处,
,,,
,,
,
,
在和中,
,
,
;
(2)设,则,
在中,由勾股定理得,
,
解得,
,
,
的面积为.
【题型4 直角三角形中过一个顶点所在直线(落点在一边上)翻折模型】
1.A
【分析】本题考查勾股定理,折叠的性质,解题关键在于求得的长. 由题意可得,,由勾股定理即可求得的长,则可得的长,然后设,则,由勾股定理,即可得方程,解方程即可求得答案.
【详解】解:点是沿折叠,点的对应点,连接,
,,
在中,,,,
,
,
设,则,
在中,,
即:,
解得:,
.
故选:A.
2.B
【分析】本题考查勾股定理,折叠的性质,先根据勾股定理求出,设,根据折叠前后对应边相等得出,,再用勾股定理解Rt DCE即可.
【详解】解:,,,
,
设,则,
由折叠的性质可得,,
,
在Rt DCE中,由勾股定理得,
,
解得,
,
故选B.
3.或1或2
【分析】本题考查了折叠的性质,勾股定理,分三种情况讨论,当时,当时,当时,利用勾股定理建立方程求解即可.
【详解】解:当时,如图,
在等腰直角三角形中,,,
∴,,
设,则,,
∵将沿翻折,
∴,,
∴,即,
解得;
∴
当时,如图,
此时,;
当时,如图,
此时,点A,B,在同一直线上,;
综上,当有一边与垂直时,的长为或1或2.
故答案为:或1或2.
4.(1)解:在中,,,
.
由题意知,,.
.
设,则,.
在中,,
.
解得.
.
(2)由题意知,
设,则.
在中,,
.
解得.
.
【题型5 直角三角形中过斜边中点所在直线翻折模型】
1.C
【分析】本题考查的是图形翻折变换的性质及勾股定理,先设,再根据图形翻折变换的性质得出,再根据勾股定理求出的值.
【详解】解:设,则,
是 ADE翻折而成,
,
在中,,
即,
解得.
故选:C.
2.
【分析】本题考查勾股定理的折叠问题,设,由折叠可知,,在中,根据列出方程求解是解决问题的关键.
【详解】解:设,则,
由折叠可知,,
在中,,即:,
解得:,即,
∴点坐标是,
故答案为:.
3.解:在中由于,,,
由勾股定理得:,
∵由折叠可知, ,
设,则.
在中,,
即,解得,
∴.
4.(1)解:在中,
,
由翻折的性质可知:,,
∵,
∴,
∴,
又∵,
∴,
∴.
(2), 理由如下:
过点作交延长线于点,连接,如图:
∴,
在和中,
,
∴,
∴,
又∵,
∴,
∵,
∴,
∴,
∴.
【题型6 直角三角形中过任意两点所在直线(落在其中一边)翻折模型】
1.解:设,则,
沿直线折叠B落在处,
,
点为的三等分点,,
或,
当时,在中,
,即,
解得:;
当时,在中,
,即,
解得:,
综上所述,的长度为或3.
2.C
【分析】本题主要考查的是翻折的性质、勾股定理的应用,熟练掌握勾股定理的运用,从而列出关于x的方程是解题的关键.
设,由翻折的性质可知,在中利用勾股定理列方程求解即可得到答案.
【详解】解:设,
由翻折的性质可知,
∵D是的中点,
,
在中,由勾股定理得:
即,
解得:,
∴,
故选:C.
3.D
【分析】本题考查了折叠的性质、勾股定理,由题意得出,由折叠的性质可得,则,再勾股定理计算即可得出答案.
【详解】解:点为的中点,
,
由折叠的性质可得:,
设,则,
由勾股定理可得:,
,
解得:,
,
故选:D.
4.(1)解:若点和顶点重合,由折叠的性质可得:,
设,则,
由勾股定理得:,
,
解得:,
;
(2)解:点落在直角边的中点上,
,
由折叠的性质可得:,
设,则,
由勾股定理可得:,
,
解得:,
∴.
【题型1 长方形中折痕过对角线模型】
1.如图所示,把一张长方形纸片沿对角线折叠,若,求的长.
2.如图,在长方形ABCD中,,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于F,,则( )
A. B.3 C. D.6
3.如图,在长方形纸片中,,. 把长方形纸片沿直线折叠,点落在点处,交于点,则的长为( )
A. B. C. D.
4.如图,长方形ABCD中,,,如果将该长方形沿对角线BD折叠,使点C落在点F处,那么图中阴影部分的面积是______.
【题型2 长方形中折痕过一顶点模型】
1.如图,长方形纸片中,已知,折叠纸片使边与对角线重合,点B落在点F处,折痕为,且.
(1)求的长;
(2)求的长.
2.如图,将长方形纸片折叠,使边落在对角线上,折痕为,且D点落在对角线上处,若,则的长为( )
A. B.3 C.1 D.
3.如图,将长方形沿折叠,点D恰好落在边的F点上,已知,,则 .
4.如图所示,有一张长方形纸片,,.现折叠该纸片使得边与对角线重合,折痕为,点落在处,求 .
【题型3 长方形中折痕过任意两点模型】
1.如图,长方形纸片中,,,将此长方形纸片折叠,使点与点重合,点落在点的位置,折痕为,则的长度为( )
A.6 B.10 C.24 D.48
2.如图,将长方形纸片沿折叠,使顶点C恰好落在边的中点上.若,,求的长.
3.已知,如图长方形中,,,将此长方形折叠,使点与点重合,折痕为,求的面积.
4.如图,长方形中,边,.将此长方形沿折叠,使点与点重合,点落在点处.
(1)证明;
(2)求的面积.
【题型4 直角三角形中过一个顶点所在直线(落点在一边上)翻折模型】
1.如图,有一块的纸片,,,,将沿折叠,使点落在上的处,连接,则的长为( )
A. B. C. D.
2.如图所示,有一块直角三角形纸片,,,,将斜边翻折,使得点B恰好落在直角边的延长线上的点E处,折痕为,则的长为( )
A. B. C. D.
3.如图,在等腰直角三角形中,,,点P是边上任意一点,连接,将沿翻折,点B的对应点为,当有一边与垂直时,的长为 .
4.如图是一张直角三角形纸片,,,.
(1)在图1中,将直角边沿折叠,使点落在斜边上的点处,求的长;
(2)在图2中,将沿折叠,使点与点重合,求的长.
【题型5 直角三角形中过斜边中点所在直线翻折模型】
1.如图,直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为.则的长是( )
A. B. C. D.
2.如图,在直角坐标系中,C点在线段上,D点在线段上,将沿直线折叠后,B点与A重合,则点C坐标是 .
3.如图,在中,,,.将按如图所示的方式折叠,使B,C两点重合,折痕为.求的长.
4.如图、为一块直角三角形纸片,.
【问题初探】:直角三角形纸片的对折问题,可以通过全等变换把所求线段转化成直角三角形的边,进而通过勾股定理来解决,体现数学中的转化思想.
(1)如图1,现将纸片沿直线折叠,使直角边落在斜边上,的对应点为,若,求的长.
【学以致用】
(2)如图2,若将直角沿折叠,点与中点重合,点分别在,上,则之间有怎样的数量关系?并证明你的结论.
【题型6 直角三角形中过任意两点所在直线(落在其中一边)翻折模型】
1.在中,,将沿直线折叠,使B落在的三等分点处,求的长.
2.如图,在中,,,.将折叠,使点落在的中点处,折痕为,则线段的长为( )
A. B. C.5 D.4
3.如图,在中,,,,将它的锐角翻折,使得点落在边的中点处,折痕交边于点,交边于点,则的长为( )
A.3 B.4 C. D.
4.在中,,,,分别是斜边和直角边上的点.把沿着直线折叠,顶点的对应点是点.
(1)如图1,若点和顶点重合,求的长;
(2)如图2,若点落在直角边的中点上,求的长.
参考答案
【题型1 长方形中折痕过对角线模型】
1.解:∵一张长方形纸片沿对角线折叠,
∴,
∴,
∴,
∴,
设,则,
在中,由勾股定理得
∴,
解得,
∴ .
2.A
【分析】根据折叠的性质,可知BF=DF=-EF,在Rt中,由勾股定理得:,由此即可求得EF值.
【详解】解:∵,,∴AD=,,
由折叠可知,AB=BE=6,AD=ED=,,,
∵,∴∠BDF=∠DBF∴BF=DF=-EF,
∴在Rt中,由勾股定理得:,
∴,解得:EF=,故选:A.
3.A
【分析】由已知条件可证△CFE≌△AFD,得到DF=EF,利用折叠知AE=AB=8cm,设AF=xcm,则DF=(8-x)cm,在Rt△AFD中,利用勾股定理即可求得x的值.
【解析】∵四边形ABCD是长方形,∴∠B=∠D=900,BC=AD,
由翻折得AE=AB=8m,∠E=∠B=900,CE=BC=AD
又∵∠CFE=∠AFD∴△CFE≌△AFD ∴EF=DF设AF=xcm,则DF=(8-x)cm
在Rt△AFD中,AF2=DF2+AD2,AD=6cm, 故选择A.
4.
【分析】要求阴影部分的面积就要先求得它的底和高,这个三角形的高就是,,由此关系就可利用勾股定理求出AE及EF的长,从而求三角形的面积.
【详解】解:四边形ABCD是矩形,,,,,
由折叠的性质,可得,,,,,
设,则,
,即,解得,.故答案为.
【题型2 长方形中折痕过一顶点模型】
1.(1)解:∵长方形纸片中,,折叠纸片使边与对角线重合,
∴,
∴,,
∴;
(2)∵折叠,
∴,
设,则:,
在中,,
∴,
∴,
∴.
2.B
【分析】本题考查矩形的折叠,勾股定理,熟练掌握运用勾股定理解决长方形的折叠是解题的关键.首先利用勾股定理计算出的长,再根据折叠可得,设,则,再根据勾股定理可得方程,再解方程即可.
【详解】∵,
∴,
∴根据勾股定理得,
根据折叠可得:,
∴,
设,则,
在中:,即,
解得:,
故答案为:B.
3.10
【分析】本题考查了折叠的性质、勾股定理,根据折叠的性质得出,设,则,根据勾股定理得出,求出,即可得出答案.
【详解】解:根据折叠的性质,,
长方形中,
设,则,
在中,由勾股定理得:,
即,
解得:,
∴,
故答案为:10.
4.3
【分析】本题考查了勾股定理与折叠问题;
先利用勾股定理求出,然后根据折叠的性质得到,,,求出,然后在中,利用勾股定理构建方程,即可求出.
【详解】解:∵,,,
∴,
由折叠得:,,,
∴,,
在中,,
∴,
∴,
故答案为:3.
【题型3 长方形中折痕过任意两点模型】
1.B
【分析】本题考查了勾股定理与折叠问题;由折叠可知,设利用勾股定理进行分析计算即可.
【详解】解:由折叠可知,
设
由勾股定理可得,
即,
解得,
,
故选:B.
2.解:由折叠的性质可得,
设,则,
∵是边的中点,
∴,
由长方形的性质可得,
在中,由勾股定理得,
∴,
解得,
∴.
3.解:过点作于点,
过点作于点,
四边形是长方形
四边形是矩形
设,
由折叠知,
,
在中,
解得,
,
,
又,
,
,
∴的面积为
4.(1)解:证明:四边形是长方形,
,,
将此长方形沿折叠,使点与点重合,点落在点处,
,,,
,,
,
,
在和中,
,
,
;
(2)设,则,
在中,由勾股定理得,
,
解得,
,
,
的面积为.
【题型4 直角三角形中过一个顶点所在直线(落点在一边上)翻折模型】
1.A
【分析】本题考查勾股定理,折叠的性质,解题关键在于求得的长. 由题意可得,,由勾股定理即可求得的长,则可得的长,然后设,则,由勾股定理,即可得方程,解方程即可求得答案.
【详解】解:点是沿折叠,点的对应点,连接,
,,
在中,,,,
,
,
设,则,
在中,,
即:,
解得:,
.
故选:A.
2.B
【分析】本题考查勾股定理,折叠的性质,先根据勾股定理求出,设,根据折叠前后对应边相等得出,,再用勾股定理解Rt DCE即可.
【详解】解:,,,
,
设,则,
由折叠的性质可得,,
,
在Rt DCE中,由勾股定理得,
,
解得,
,
故选B.
3.或1或2
【分析】本题考查了折叠的性质,勾股定理,分三种情况讨论,当时,当时,当时,利用勾股定理建立方程求解即可.
【详解】解:当时,如图,
在等腰直角三角形中,,,
∴,,
设,则,,
∵将沿翻折,
∴,,
∴,即,
解得;
∴
当时,如图,
此时,;
当时,如图,
此时,点A,B,在同一直线上,;
综上,当有一边与垂直时,的长为或1或2.
故答案为:或1或2.
4.(1)解:在中,,,
.
由题意知,,.
.
设,则,.
在中,,
.
解得.
.
(2)由题意知,
设,则.
在中,,
.
解得.
.
【题型5 直角三角形中过斜边中点所在直线翻折模型】
1.C
【分析】本题考查的是图形翻折变换的性质及勾股定理,先设,再根据图形翻折变换的性质得出,再根据勾股定理求出的值.
【详解】解:设,则,
是 ADE翻折而成,
,
在中,,
即,
解得.
故选:C.
2.
【分析】本题考查勾股定理的折叠问题,设,由折叠可知,,在中,根据列出方程求解是解决问题的关键.
【详解】解:设,则,
由折叠可知,,
在中,,即:,
解得:,即,
∴点坐标是,
故答案为:.
3.解:在中由于,,,
由勾股定理得:,
∵由折叠可知, ,
设,则.
在中,,
即,解得,
∴.
4.(1)解:在中,
,
由翻折的性质可知:,,
∵,
∴,
∴,
又∵,
∴,
∴.
(2), 理由如下:
过点作交延长线于点,连接,如图:
∴,
在和中,
,
∴,
∴,
又∵,
∴,
∵,
∴,
∴,
∴.
【题型6 直角三角形中过任意两点所在直线(落在其中一边)翻折模型】
1.解:设,则,
沿直线折叠B落在处,
,
点为的三等分点,,
或,
当时,在中,
,即,
解得:;
当时,在中,
,即,
解得:,
综上所述,的长度为或3.
2.C
【分析】本题主要考查的是翻折的性质、勾股定理的应用,熟练掌握勾股定理的运用,从而列出关于x的方程是解题的关键.
设,由翻折的性质可知,在中利用勾股定理列方程求解即可得到答案.
【详解】解:设,
由翻折的性质可知,
∵D是的中点,
,
在中,由勾股定理得:
即,
解得:,
∴,
故选:C.
3.D
【分析】本题考查了折叠的性质、勾股定理,由题意得出,由折叠的性质可得,则,再勾股定理计算即可得出答案.
【详解】解:点为的中点,
,
由折叠的性质可得:,
设,则,
由勾股定理可得:,
,
解得:,
,
故选:D.
4.(1)解:若点和顶点重合,由折叠的性质可得:,
设,则,
由勾股定理得:,
,
解得:,
;
(2)解:点落在直角边的中点上,
,
由折叠的性质可得:,
设,则,
由勾股定理可得:,
,
解得:,
∴.
同课章节目录
