1.3《勾股定理的应用》小节复习题(含解析)八年级数学上册北师大版
文档属性
| 名称 | 1.3《勾股定理的应用》小节复习题(含解析)八年级数学上册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 11:37:44 | ||
图片预览


文档简介
1.3《勾股定理的应用》小节复习题
【题型1 应用勾股定理解决梯子滑落高度】
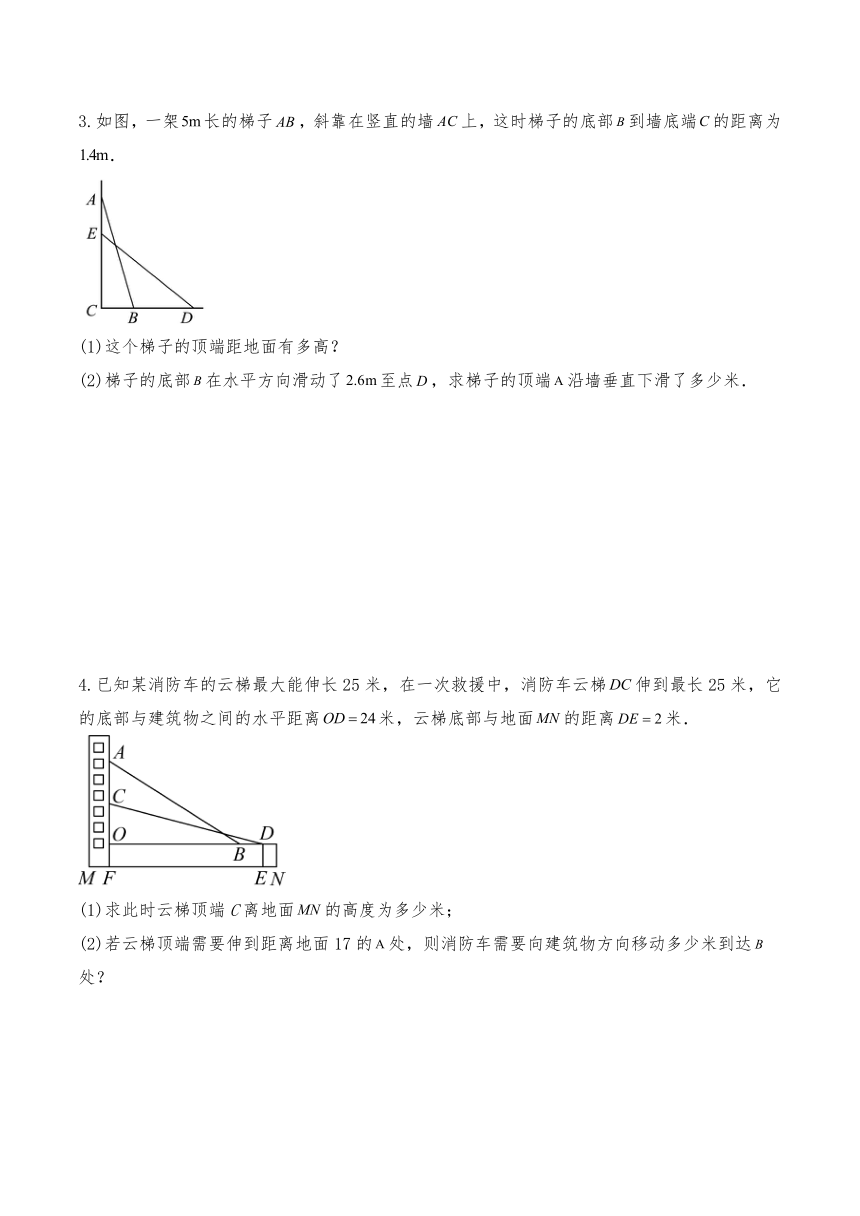
1.每年的11月9日是我国的消防日,为了增强全民的消防安全意识,某校师生举行了消防演练,如图,云梯长为25米,云梯顶端C靠在教学楼外墙上(墙与地面垂直),云梯底端A与墙角O的距离为7米.
(1)求云梯顶端C与墙角O的距离的长;
(2)现云梯顶端C下方4米D处发生火灾,需将云梯顶端C下滑到着火点D处,则云梯底端水平方向向右滑动的距离为多少米.
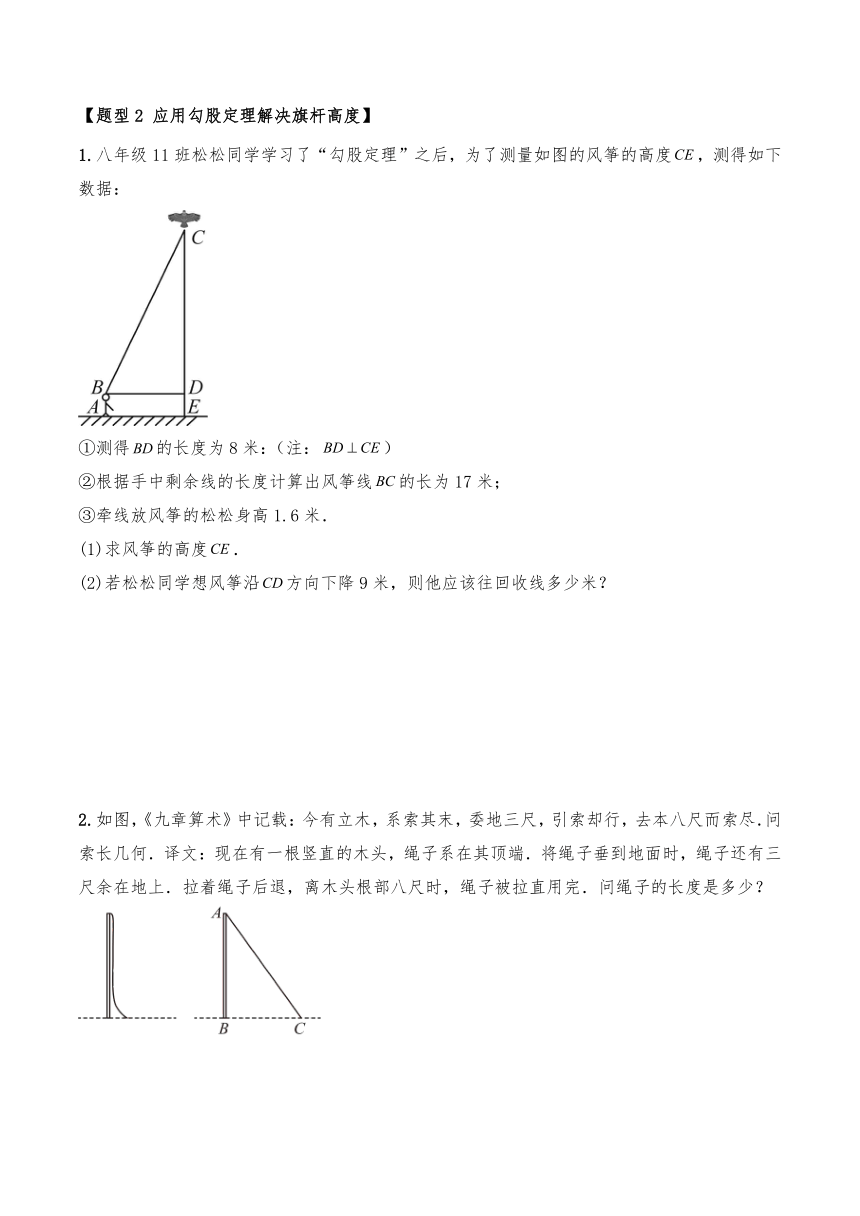
2.如图,一架长5米的梯子斜靠在墙上,到墙底端C的距离为3米,此时梯子的高度达不到工作要求,因此把梯子的端向墙的方向移动了米到B处,此时梯子的高度达到工作要求,求梯子的端向上移动了多少米.
3.如图,一架长的梯子,斜靠在竖直的墙上,这时梯子的底部到墙底端的距离为.
(1)这个梯子的顶端距地面有多高?
(2)梯子的底部在水平方向滑动了至点,求梯子的顶端沿墙垂直下滑了多少米.
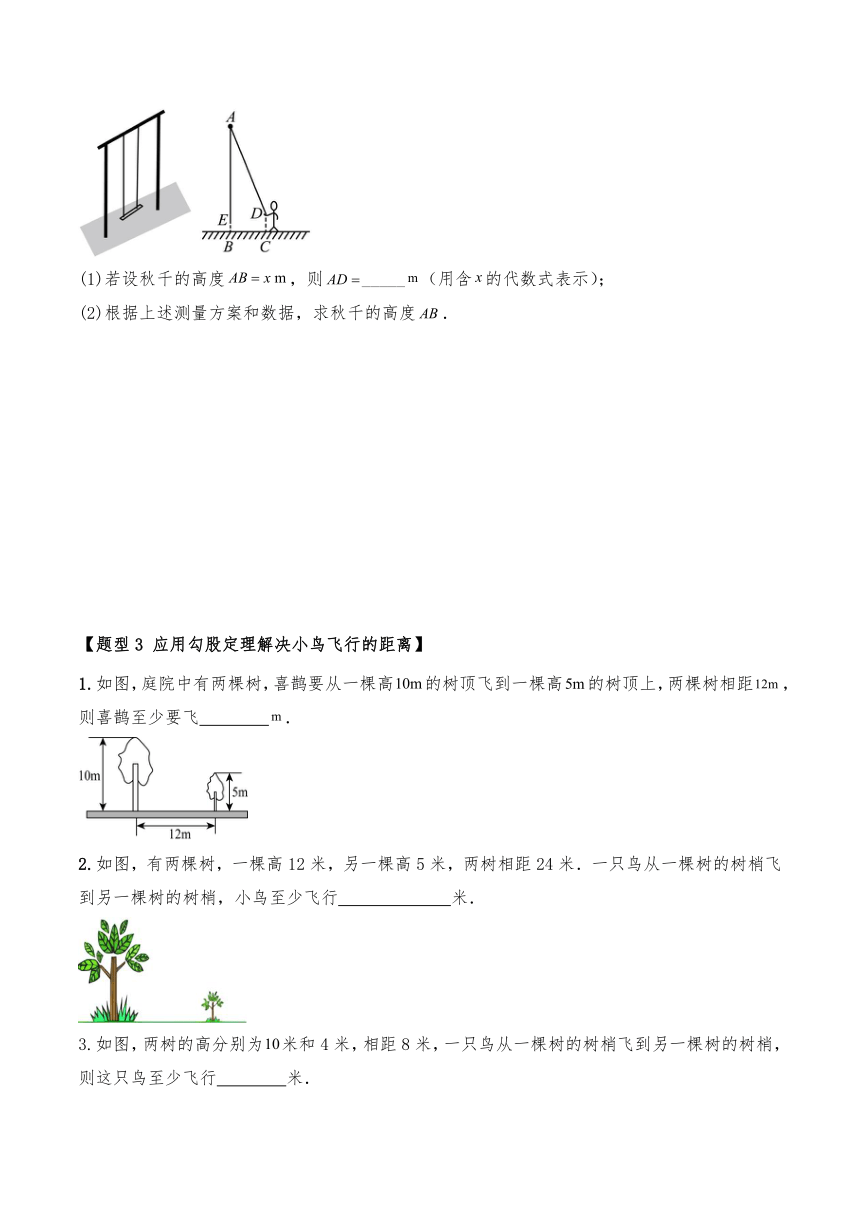
4.已知某消防车的云梯最大能伸长25米,在一次救援中,消防车云梯伸到最长25米,它的底部与建筑物之间的水平距离米,云梯底部与地面的距离米.
(1)求此时云梯顶端C离地面的高度为多少米;
(2)若云梯顶端需要伸到距离地面17的处,则消防车需要向建筑物方向移动多少米到达处?
【题型2 应用勾股定理解决旗杆高度】
1.八年级11班松松同学学习了“勾股定理”之后,为了测量如图的风筝的高度,测得如下数据:
①测得的长度为8米:(注:)
②根据手中剩余线的长度计算出风筝线的长为17米;
③牵线放风筝的松松身高1.6米.
(1)求风筝的高度.
(2)若松松同学想风筝沿方向下降9米,则他应该往回收线多少米?
2.如图,《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:现在有一根竖直的木头,绳子系在其顶端.将绳子垂到地面时,绳子还有三尺余在地上.拉着绳子后退,离木头根部八尺时,绳子被拉直用完.问绳子的长度是多少?
3.如图,同学们想测量旗杆的高度(米),他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:
小明:①测量出绳子垂直落地后还剩余米,如图:
②把绳子拉直,绳子末端在地面上离旗杆底部的距离米,如图.
小亮:先在旗杆底端的绳子上打了一个结,然后举起绳结拉到如图3点处,作垂直于点,.
(1)请你按小明的方案求出旗杆的高度;
(2)在()的条件下,已知小亮举起绳结离旗杆的距离米,求此时绳结到地面的高度.
4.阅读下列材料,回答问题.
社区公园里新安装了一架秋千,小白对秋千的高度产生了兴趣,星期天他和朋友一起带着卷尺到公园测量秋千的高度,他设计如下的测量方案:
步骤一:测得秋千静止时的底端与地面的距离;
步骤二:如图,小白握住秋千的底端往外后退,直到秋千的绳索被拉直,测得此时秋千底端离地面的高度,再测得小白站立处与秋千静止时的水平距离.
(1)若设秋千的高度,则_____(用含的代数式表示);
(2)根据上述测量方案和数据,求秋千的高度.
【题型3 应用勾股定理解决小鸟飞行的距离】
1.如图,庭院中有两棵树,喜鹊要从一棵高的树顶飞到一棵高的树顶上,两棵树相距,则喜鹊至少要飞 .
2.如图,有两棵树,一棵高12米,另一棵高5米,两树相距24米.一只鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行 米.
3.如图,两树的高分别为米和4米,相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,则这只鸟至少飞行 米.
4.如图,一条路的两边有两棵树,一棵树高为11米,另一棵树高为6米,两树的距离为12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行 米.
【题型4 应用勾股定理解决大树折断前的高度】
1.《九章算术》中记“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:竹子折断处离地面有几尺?(1丈尺)
2.如图,一根直立的旗杆高,因刮大风旗杆从点处折断,顶部着地且离旗杆底部的距离为.
(1)求旗杆在距地面多高处折断;
(2)工人在修复的过程中,发现在折断点的下方的点处,有一明显裂痕,若下次大风将旗杆从点处吹断,在距离旗杆底部5米处是否有被砸伤的风险?
3.如图,有两棵树,一棵高米(米),另一棵高米(米),两树相距米(米).
(1)求一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?
(2)如图,台风过后,高米的树在点处折断,大树顶部落在点处,则树折断处距离地面多少米?
4.如图,一根垂直于地面的旗杆高,因刮大风旗杆从点处折断,顶部着地且离旗杆底部的距离.
(1)求旗杆折断处点距离地面的高度;
(2)工人在修复的过程中,发现在折断处的下方1.4m的点处,有一明显裂痕,若下次大风将修复好的旗杆从点处吹断,旗杆的顶部落在水平地面上的处,形成一个,请求出的长.
【题型5 应用勾股定理解决水杯中的筷子问题】
1.如图,一根长的牙刷放置于底面半径是,高为的圆柱水杯中,牙刷露在杯子外面的长度为,求.
2.“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即,,,,求的长.
3.如图,一种圆柱形的饮料杯,测得内部底面圆半径为,杯高,点,点在内部底面圆上,线段经过杯子的内部底面圆心.将吸管一端放在点处,并让吸管经过点(按如图所示)放进杯里,要求杯门外面至少要露出长的吸管,问至少需要制作多长的吸管?
4.《九章算术》卷九“勾股”中记载:今有池,方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,问水深、葭长各几何.大意是:如图,水池底面的宽丈,芦苇生长在的中点O处,高出水面的部分尺.将芦苇向池岸牵引,尖端达到岸边时恰好与水面平齐,即, 求水池的深度和芦苇的长度(1丈等于10尺).
(1)求水池的深度;
(2)中国古代数学家刘徽在为《九章算术》作注解时,更进一步给出了这类问题的一般解法.他的解法用现代符号语言可以表示为:若已知水池宽, 芦苇高出水面的部分,则水池的深度可以通过公式计算得到.请证明刘徽解法的正确性.
【题型6 应用勾股定理解决航海问题】
1.如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东方向开往B岛,其速度仍为20海里/小时.
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?(结果保留一位小数)
2.某日我海防巡逻艇在A处探测到在它正东方向距它30海里的B处有一艘可疑船只,该船只正以每小时36海里的速度沿北偏西方向行驶,巡逻艇立即沿北偏东的方向前往拦截,半小时后恰好在C处拦截到该船只.
(1)求巡逻艇的速度为每小时多少海里?
(2)求此时该船只所在处C与的距离为多少海里?
3.如图,一艘船由A岛沿北偏东方向航行至B岛,然后再沿北偏西方向航行至C岛.
(1)求A,C两岛之间的距离;
(2)确定C岛在A岛的什么方向?
4.如图,小岛A位于港口C北偏西方向上,小岛B位于港口C的北偏东方向上,且与港口C相距200海里,小岛B与小岛A相距250海里.
(1)求小岛A与港口C的距离;
(2)在小岛B处有一艘载满货物的货船,以每小时20海里的速度从小岛B出发沿B→A方向航行,当货船距离港口C最近时,求货船还需航行多长时间才能到达小岛A?
【题型7 应用勾股定理解决河的宽度】
1.如图,池塘边有两点,点是与方向成直角的方向上一点,测得长为米,长为米.求两点间的距离(取).
2.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点A处偏离欲到达地点B处,结果他在水中实际游的路程比河的宽度多.求该河的宽度的长.
3.如图,湖的两岸有两棵景观树,在与垂直的方向上取一点,测得米,米.求两棵景观树之间的距离.
4.如图,某渡船从点B处沿着与河岸垂直的路线横渡,由于受水流的影响,实际沿着航行,上岸地点C与欲到达地点A相距70米,结果发现比河宽多10米.
(1)求该河的宽度;(两岸可近似看作平行)
(2)设实际航行时,速度为每秒5米,从C回到A时,速度为每秒4米,求航行总时间.
【题型8 应用勾股定理解决台阶上地毯长度】
1.某学校为防止雨天地滑,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图所示,已知,,.
(1)求的长;
(2)若已知楼梯宽,每平方米地毯25元,需要花费多少钱地毯才能铺满所有台阶.(假设地毯在铺的过程中没有损耗)
2.如图,小明与小华爬山时遇到一条笔直的石阶路,路的一侧设有与坡面平行的护栏.小明量得每一级石阶的宽为,高为,爬到山顶后,小华数得石阶一共200级,若每一级石阶的宽和高都一样,且构成直角,请你帮他们求护栏的长度.
3.如图,楼梯的高度为,楼梯坡面的长度为,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?(精确到)
4.某会展中心在会展期间准备将高、长、宽的楼道铺上地毯,已知地毯每平方米30元,请你帮助计算一下,铺完这个楼道至少需要多少元?
【题型9 应用勾股定理解决汽车是否超速问题】
1.已知某高速路段限速(即).如图,汽车在车速检测仪A正前方30米的处,过了后到处,测得.请通过计算判断汽车是否超速.
2.某条道路限速,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到车速检测仪A正下方的B处,过了,小汽车到达C处,此时测得小汽车与车速检测仪间的距离为.
(1)求的长;
(2)这辆小汽车超速了吗?
3.如图所示,点装有一车速检测仪,它到公路边的距离米,小汽车行驶过检测仪监控区域,到达点时开始计时,离开点时停止计时,已知米.
(1)若一辆汽车以的速度匀速通过监控区域,共用时几秒?
(2)若另一辆车通过监控区域共用时3秒,该车是否超速?请说明理由.
4.如图,一辆小汽车在一条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方120米的处,过了8秒,小汽车到达处,此时测得小汽车与车速检测仪间的距离为200米.
(1)求的长;
(2)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,这辆小汽车在段是否超速行驶?请说明理由(参考数据:)
【题型10 应用勾股定理解决是否受台风影响问题】
1.由于过度采伐森林和破坏植物,使我国许多地区频频遭受沙尘暴的侵袭.近日市气象局测得沙尘中心在市正西方向千米的处,以千米/时的速度向东偏南的方向移动,距离沙尘中心千米的范围是受沙尘暴严重影响的区域.
(1)问市会不会受到沙尘暴的严重影响?请通过计算说明理由;
(2)若受影响请计算市受影响的时间.
2.某市夏季经常受台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向由点行驶向点,已知点为一海港,当时,点到,两点的距离分别为和,以台风中心为圆心周围以内为受影响区域.
(1)海港受台风影响吗?为什么?
(2)若台风的速度为,则台风影响该海港持续的时间有多长?
3.如图,两条公路、交于点,在公路旁有一学校,与点的距离为,点(学校)到公路的距离为,一大货车从点出发,行驶在公路上,货车周围范围内有噪音影响.
(1)货车开过学校是否受噪音影响?为什么?
(2)若货车速度为,则学校受噪音影响多少秒钟?
4.2024年9月第11号台风“摩羯”登陆,使我国很多地区受到严重影响.据报道,这是今年以来对我国影响最大的台风,风力影响半径(即以台风中心为圆心,为半径的圆形区域都会受台风影响).如图,线段是台风中心从市移动到市的大致路线,是某个大型农场,且.若之间相距之间相距.
(1)判断农场是否会受到台风的影响,请说明理由;
(2)若台风中心的移动速度为,则台风影响该农场持续时间有多长?
【题型11 应用勾股定理解决选扯距离相离问题】
1.如图,铁路上有、两点(看作直线上两点)相距千米,、为两村庄(看作两个点),,,垂足分别为、,千米,千米,现在要在铁路旁修建一个煤栈,使得、两村到煤栈的距离相等.
设煤栈应建在距点千米处的点处,如图,则千米.
(1)(______)千米;
(2)煤栈应建在距点多少千米处?
2.如图,已知某学校A与直线公路相距300米(即米,),且与该公路上一个车站D相距500米(即米),现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市 C 与车站D的距离是多少米
3.如图,铁路上A,B两点相距,C,D两点为两村庄,于点A,于点B,已知,,现在要在铁路上建一个土特产收购站E,使得C,D两村到E站的距离相等,则E站应建在距A点多少千米处?
4.如图,小区A与公路l的距离米,小区B与公路l的距离米,已知米.
(1)政府准备在公路边建造一座公交站台Q,使Q到A、B两小区的路程相等,求的长;
(2)现要在公路旁建造一利民超市P,使P到A、B两小区的路程之和最短,求的最小值,求出此最小值.
【题型12 应用勾股定理解决几何图形中最短路径问题】
1.【实践发现】数学兴趣小组在研究蚂蚁在圆柱侧面爬行问题时,发现蚂蚁沿圆柱侧面从一点爬到另一点的最短路径问题与圆柱的展开图有关.
【实践探究】设计测量方案:
第一步:测量圆柱的底面半径,测得圆柱底面半径是2厘米;
第二步:测量圆柱的高,测得圆柱的高为4厘米;
第三步:如图,假设蚂蚁在圆柱侧面从点A爬到点B,研究其最短路径情况.
【问题解决】设蚂蚁爬行的最短路径长度为厘米,通过计算即可求得最短路径长度.
(1)根据题意知圆柱底面半径厘米,圆柱的侧面展开后是一个长方形(取3),其中一条直角边(圆柱侧面展开后长方形的高)为 厘米,另一条直角边(底面圆周长的一半)为 厘米;
(2)在展开图中,蚂蚁的最短路径是连接的线段长,请你计算蚂蚁从点爬到点的最短路程.
2.如图,长方体的底面边长分别为4cm和8cm,高为10cm,若一只蚂蚁从点开始经过4个侧面爬行一圈到达点,若蚂蚁的爬行速度为内蚂蚁能否爬到点?
3.【问题情境】
数学综合与实践活动课上,老师提出如下问题:一个三级台阶,它每一级的长、宽、高分别为20、3、2,和是一个台阶两个相对的端点.
【探究实践】
老师让同学们探究:如图①,若点处有一只蚂蚁要到点去吃可口的食物,那么蚂蚁沿着台阶爬到点的最短路程是多少?
(1)同学们经过思考得到如下解题方法:如图②,将三级台阶展开成平面图形,可得到长为20.宽为15的长方形,连接,经过计算得到长度为___________,就是最短路程.
【变式探究】
(2)如图③,是一只圆柱形玻璃杯,该玻璃杯的底面周长是,高是,若蚂蚁从点出发沿着玻璃杯的侧面到点,则蚂蚁爬行的最短距离为___________.-
【拓展应用】
(3)如图④,圆柱形玻璃杯的高,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在外壁上,离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所爬行的最短路程是多少?(杯壁厚度不计)(画出示意图并进行计算)
4.如图,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿剪开,所得的圆柱侧面展开图是______.
A. B. C. D.
(2)如图②,若将金属丝从点B绕四圈到达点A,则所需金属丝最短长度是多少?
(3)现有一个长、宽、高分别为的无盖长方体木箱(如图3,).现在箱外的点A处有一只蜘蛛,箱内的点C处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.(木板的厚度忽略不计)
参考答案
【题型1 应用勾股定理解决梯子滑落高度】
1.(1)解:在中,,,
由勾股定理得,
即,
解得:;
答:云梯顶端与墙角的距离的长为;
(2)解:,,
,
在中,,,
由勾股定理得,
即,
解得:,
,
.
答:云梯底端在水平方向上滑动的距离为.
2.解:如图所示,在中,根据勾股定理知,,
在中,,
根据勾股定理知,
.
答:梯子的端向上移动了.
3.(1)解:根据题意可知,,,
∴在中,
答:这个梯子的顶端距离地面.
(2)解:由题意得,,,
∴在中,
∴
答:梯子的顶端沿墙垂直下滑了.
4.(1)解:为长方形,
在中,由勾股定理
答:此时云梯顶端离地面的高度为9米
(2)解:,
在中,由勾股定理
答:消防车需要向建筑物方向移动4米到达B处.
【题型2 应用勾股定理解决旗杆高度】
1.(1)解:在中,
由勾股定理得,
所以,(负值舍去),
所以,(米),
答:风筝的高度为米;
(2)如图:由题意得,米,∴米,
∴,
∴米,
∴(米),
∴他应该往回收线7米.
2.解:设绳索长为x尺,则木桩高为尺,
∴在中,,,
∴根据勾股定理,得,
解得.
∴绳索长为尺.
3.(1)解:设旗杆的高度为米,则绳子的长度为米,
在中,由勾股定理得,,
解得,
答:旗杆的高度为米;
(2)解:由题意可知,米, 米,,
在中,由勾股定理得米,
∴米,
∴米,
答:此时绳结到地面的高度为米.
4.(1)解:由题意得,,
故答案为:;
(2)解:过点作,垂足为,
则,,
,
,
在中,,
,
即,
解得:,
答:秋千的高度为.
【题型3 应用勾股定理解决小鸟飞行的距离】
1.13
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题考查了勾股定理的应用,根据勾股定理,进行计算即可求解.
【详解】解:如图,
根据题意得:,
∴.
即喜鹊至少要飞.
故答案为:13
2.25
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题考查正确运用勾股定理.根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出即可.
【详解】解:如图,设大树高为米,小树高为米,
连接,平移到,则米,,两树相距米,
∴(米),
在中,(米),
故小鸟至少飞行米.
故答案为:25.
3.
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题主要考查了勾股定理的应用,根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出,熟练掌握其性质,合理添加辅助线是解决此题的关键.
【详解】如图,过C点作于E,则四边形是矩形,连接,
设大树高为,小树高为,
∴,,,
在中,
答:小鸟至少飞行米,
故答案为:
4.13
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题考查了勾股定理,过C作平行地面,连接,由题意得米,米,由勾股定理可得的长,即小鸟至少要飞行的距离.
【详解】解:过C作平行地面,连接,
由题意得,米,米,米,
由勾股定理得,米,
故答案为:13.
【题型4 应用勾股定理解决大树折断前的高度】
1.解:设竹子折断处离地面有尺,
由题意得:,,,,
∴,
则:,
解得:.
答:竹子折断处离地面有4.2尺.
2.(1)解:由题意,知.
因为,
设长为,则长,
则,
解得.
故旗杆距地面处折断;
(2)解:如图:
因为点P距地面,
所以,
所以,
则距离旗杆底部周围的范围内有被砸伤的风险,
所以在距离旗杆底部处有被砸伤的风险.
3.(1)解:两棵树的高度差为(米),两树相距米(米),
根据勾股定理可得:小鸟至少飞行的距离(米),
答:至少飞了米;
(2)解:由勾股定理得:,
,
解得:,
答:树折断处距离地面米.
4.(1)解:由题意可知:米,
,
,
又米,
,
米;
(2)解:点距地面米,
米,
(米.
【题型5 应用勾股定理解决水杯中的筷子问题】
1.解:如图,在中,,
根据勾股定理得
.
2.解:设,则,
由题意,得:,
解得:,即.
3.解:由题意可知 ABC是直角三角形,,,线段为内部底面圆直径,
内部底面圆半径为,
,
在中,
,
解得:或(舍去,不符合题意)
答:至少需要制作长的吸管.
4.(1)解:设水池深度为x尺,则芦苇高度为尺,
由题意有:尺;
为中点,且丈尺,
(尺);
在中,由勾股定理得:,
即,
解得:;
即尺;
答:水池的深度为12尺;
(2)证明:水池深度,则芦苇高度为,
由题意有:;
为中点,且,
;
在中,由勾股定理得:,
即,
整理得:;
表明刘徽解法是正确的.
【题型6 应用勾股定理解决航海问题】
1.(1)解:过点B作于点D,
在中,,设,则,
在中,,
则,,
由得,
解得,
,
答:港口A到海岛B的距离为海里;
(2)解:甲船看见灯塔所用时间:小时,
乙船看见灯塔所用时间:小时,
所以乙船先看见灯塔.
2.(1)解:,,,
,,
,
,,
∴在中,由勾股定理得,
,
答:巡逻艇的速度为每小时48海里;
(2)解:作于,
,
,
答:此时该船只所在处C与的距离为海里.
3.(1)如图,由题意可知:,
∵,
∴,
∴,
在中,,
答:A,C两岛之间的距离是;
(2)又∵,,
∴,
∵,
∴,
∴C岛在A岛北偏西的方向上.
4.(1)解:由题意得,,.
在中,,
∴.
答:小岛A与港口C的距离为150海里;
(2)解:过点C作于点D,
当货船航行到点D时,此时货船距离港口C最近.
∵,
∴,
在中,,
∴,
∴(小时).
答:货船还需航行4.5小时才能到达小岛A.
【题型7 应用勾股定理解决河的宽度】
1.解:由题意可得,
∵米,米,
∴米,
答:两点间的距离为米.
2.解:根据题意可知:设米,则米,
在中,,,
即,
解得:,
即米,
答.该河的宽度为75米.
3.解:在Rt中,由勾股定理,得:
,
(米).
答:两棵景观树之间的距离是12米.
4.(1)解:设米,则米,
在中,根据勾股定理得:
,
解得:,
答:河宽240米.
(2)解:(秒),
(秒),
(秒),
答:航行总时间为67.5秒.
【题型8 应用勾股定理解决台阶上地毯长度】
1.(1)解:∵,,,
,
答:的长为;
(2)解:地毯长为:,
∴地毯的面积为,
每平方米地毯25元,
需要花费(元);
答:需要花费元地毯才能铺满所有台阶.
2.解:根据勾股定理,每一级石阶的斜边长为,
.
答:护栏的长度为.
3.解:如图,由勾股定理得,,
∴米,
∴米,
答:地毯的长度至少需要米.
4.解:由勾股定理得,
则地毯总长为,
则地毯的总面积为(平方米),
所以铺完这个楼道至少需要(元).
故答案为:1020.
【题型9 应用勾股定理解决汽车是否超速问题】
1.解:汽车没有超速,理由如下:
依题意,由勾股定理可得:,,,
.
∴,
∴.
∴汽车没有超速.
2.(1)解:根据题意,得,,
由勾股定理,得,
∴,
故的长为.
(2)解:,
∵,
∴这辆小汽车未超速.
3.(1)解:依题意可得,,
∴,为直角三角形
∵米,米,
∴米,
,
∴
答∶共用时4秒;
(2)解:超速,理由如下∶
,
∵,
∴该车超速.
4.(1)解:在中,,
,
答:的长为米;
(2)解:小汽车的速度为:,
,
故小汽车超速了.
【题型10 应用勾股定理解决是否受台风影响问题】
1.(1)解:过点作于,由题意得千米,,
∴(千米),
∵,
∴市会受到沙尘暴的严重影响;
(2)解:设沙尘中心距点千米处,刚好处在上的两点,
在中,千米,千米,
∴千米,
∴千米,
∴市受影响的时间为(小时),
故市受影响的时间为小时.
2.(1)解:海港受台风影响,理由如下:
如图,过点作,
∵,
∴,
∵,,
∴,
∵,
∴,
∵以台风中心为圆心周围以内为受影响区域,
∴海港受台风影响;
(2)解:如图,假设当,时,正好影响港口,
∴,,
∴,
∵台风的速度为千米/小时,
∴(小时),
答:海港受台风影响的时间会持续小时.
3.(1)解:货车开过学校受噪音影响,理由如下:
∵,
∴货车开过学校受噪音影响;
(2)解:如图,设,则路段是学校受噪音影响的路段,
∵,
∴,
又,,
∴,
同理:,
∴,
∴影响时间,
答:学校受噪音影响时间是6秒.
4.(1)解:农场会受到台风的影响,理由如下:
如图,过作于,
,
,
,
的面积,
,
,
,
农场会受到台风的影响;
(2)解:如图,台风从点开始影响该农场,到点以后结束影响,连接,,
,
,
,
由勾股定理得,
,
台风中心的移动速度为,
台风影响该农场持续时间是(小时).
【题型11 应用勾股定理解决选扯距离相离问题】
1.(1)解:如图,连接,则,
∵,,
∴,
∵千米,
∴千米,
∵,
∴,
解得,
∴千米,
故答案为:;
(2)解:由()得,千米,
∴煤栈应建在距点千米处.
2.解:根据题意得:,,
在直角三角形中,
米,米,
(米),
设米,则米,
在中,,
即,
解得:,
答:该超市C与车站D的距离是312.5米.
3.解:,两村到站的距离相等.
,
于,于,
,
,,
,
设,则,
,,
,
解得:,
.
答:站应建在离站处.
4.(1)解:如图1,
根据题意得:,
设,则,
,
解得,
即的长为475米;
(2)如图,作点A关于直线l的对称点,连接,交直线l于点P.
则,
,
的最小值为,
如图,作于点E,
在中,
米,米,
米,
的最小值为1000米.
【题型12 应用勾股定理解决几何图形中最短路径问题】
1.(1)解:已知圆柱的高为4厘米,圆柱侧面展开后长方形的高就等于圆柱的高,所以其中一条直角边为4厘米,
已知圆柱底面半径厘米,取3,根据圆的周长公式,则底面圆周长的一半为厘米,即另一条直角边为6厘米,
故答案为:,;
(2)解:(厘米),
答:蚂蚁从点爬到点的最短路程厘米.
2.解:如图,将长方体的侧面展开在同一平面内,
,
.
,
,
内蚂蚁能爬到点.
3.解:(1)由题意得,
故答案为:;
(2)将圆柱体展开,由题意得
,
故答案为:;
(3)如图,
从玻璃杯侧面展开,作关于的对称点,作交延长线于点,连接交于点,
,,
,
,
,
蚂蚁从外壁处到内壁处所爬行的最短路程是.
4.(1)解:根据题意得:将圆柱侧面沿剪开,所得的圆柱侧面展开图只有选项A符合题意,
故选:A;
(2)若将金属丝从点B绕四圈到达点A,
则所需金属丝最短长度是以底面周长4倍及高为直角三角形的斜边长为:,
∴最短长度是;
(3)①把展开,如图此时总路程为,
②把展开,如图
此时的总路程为;
③如图所示,把展开,
此时的总路程为,
由于,所以第三种方案路程更短,最短路程为.
【题型1 应用勾股定理解决梯子滑落高度】
1.每年的11月9日是我国的消防日,为了增强全民的消防安全意识,某校师生举行了消防演练,如图,云梯长为25米,云梯顶端C靠在教学楼外墙上(墙与地面垂直),云梯底端A与墙角O的距离为7米.
(1)求云梯顶端C与墙角O的距离的长;
(2)现云梯顶端C下方4米D处发生火灾,需将云梯顶端C下滑到着火点D处,则云梯底端水平方向向右滑动的距离为多少米.
2.如图,一架长5米的梯子斜靠在墙上,到墙底端C的距离为3米,此时梯子的高度达不到工作要求,因此把梯子的端向墙的方向移动了米到B处,此时梯子的高度达到工作要求,求梯子的端向上移动了多少米.
3.如图,一架长的梯子,斜靠在竖直的墙上,这时梯子的底部到墙底端的距离为.
(1)这个梯子的顶端距地面有多高?
(2)梯子的底部在水平方向滑动了至点,求梯子的顶端沿墙垂直下滑了多少米.
4.已知某消防车的云梯最大能伸长25米,在一次救援中,消防车云梯伸到最长25米,它的底部与建筑物之间的水平距离米,云梯底部与地面的距离米.
(1)求此时云梯顶端C离地面的高度为多少米;
(2)若云梯顶端需要伸到距离地面17的处,则消防车需要向建筑物方向移动多少米到达处?
【题型2 应用勾股定理解决旗杆高度】
1.八年级11班松松同学学习了“勾股定理”之后,为了测量如图的风筝的高度,测得如下数据:
①测得的长度为8米:(注:)
②根据手中剩余线的长度计算出风筝线的长为17米;
③牵线放风筝的松松身高1.6米.
(1)求风筝的高度.
(2)若松松同学想风筝沿方向下降9米,则他应该往回收线多少米?
2.如图,《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:现在有一根竖直的木头,绳子系在其顶端.将绳子垂到地面时,绳子还有三尺余在地上.拉着绳子后退,离木头根部八尺时,绳子被拉直用完.问绳子的长度是多少?
3.如图,同学们想测量旗杆的高度(米),他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学应用勾股定理分别提出解决这个问题的方案如下:
小明:①测量出绳子垂直落地后还剩余米,如图:
②把绳子拉直,绳子末端在地面上离旗杆底部的距离米,如图.
小亮:先在旗杆底端的绳子上打了一个结,然后举起绳结拉到如图3点处,作垂直于点,.
(1)请你按小明的方案求出旗杆的高度;
(2)在()的条件下,已知小亮举起绳结离旗杆的距离米,求此时绳结到地面的高度.
4.阅读下列材料,回答问题.
社区公园里新安装了一架秋千,小白对秋千的高度产生了兴趣,星期天他和朋友一起带着卷尺到公园测量秋千的高度,他设计如下的测量方案:
步骤一:测得秋千静止时的底端与地面的距离;
步骤二:如图,小白握住秋千的底端往外后退,直到秋千的绳索被拉直,测得此时秋千底端离地面的高度,再测得小白站立处与秋千静止时的水平距离.
(1)若设秋千的高度,则_____(用含的代数式表示);
(2)根据上述测量方案和数据,求秋千的高度.
【题型3 应用勾股定理解决小鸟飞行的距离】
1.如图,庭院中有两棵树,喜鹊要从一棵高的树顶飞到一棵高的树顶上,两棵树相距,则喜鹊至少要飞 .
2.如图,有两棵树,一棵高12米,另一棵高5米,两树相距24米.一只鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行 米.
3.如图,两树的高分别为米和4米,相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,则这只鸟至少飞行 米.
4.如图,一条路的两边有两棵树,一棵树高为11米,另一棵树高为6米,两树的距离为12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少要飞行 米.
【题型4 应用勾股定理解决大树折断前的高度】
1.《九章算术》中记“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:竹子折断处离地面有几尺?(1丈尺)
2.如图,一根直立的旗杆高,因刮大风旗杆从点处折断,顶部着地且离旗杆底部的距离为.
(1)求旗杆在距地面多高处折断;
(2)工人在修复的过程中,发现在折断点的下方的点处,有一明显裂痕,若下次大风将旗杆从点处吹断,在距离旗杆底部5米处是否有被砸伤的风险?
3.如图,有两棵树,一棵高米(米),另一棵高米(米),两树相距米(米).
(1)求一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?
(2)如图,台风过后,高米的树在点处折断,大树顶部落在点处,则树折断处距离地面多少米?
4.如图,一根垂直于地面的旗杆高,因刮大风旗杆从点处折断,顶部着地且离旗杆底部的距离.
(1)求旗杆折断处点距离地面的高度;
(2)工人在修复的过程中,发现在折断处的下方1.4m的点处,有一明显裂痕,若下次大风将修复好的旗杆从点处吹断,旗杆的顶部落在水平地面上的处,形成一个,请求出的长.
【题型5 应用勾股定理解决水杯中的筷子问题】
1.如图,一根长的牙刷放置于底面半径是,高为的圆柱水杯中,牙刷露在杯子外面的长度为,求.
2.“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即,,,,求的长.
3.如图,一种圆柱形的饮料杯,测得内部底面圆半径为,杯高,点,点在内部底面圆上,线段经过杯子的内部底面圆心.将吸管一端放在点处,并让吸管经过点(按如图所示)放进杯里,要求杯门外面至少要露出长的吸管,问至少需要制作多长的吸管?
4.《九章算术》卷九“勾股”中记载:今有池,方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,问水深、葭长各几何.大意是:如图,水池底面的宽丈,芦苇生长在的中点O处,高出水面的部分尺.将芦苇向池岸牵引,尖端达到岸边时恰好与水面平齐,即, 求水池的深度和芦苇的长度(1丈等于10尺).
(1)求水池的深度;
(2)中国古代数学家刘徽在为《九章算术》作注解时,更进一步给出了这类问题的一般解法.他的解法用现代符号语言可以表示为:若已知水池宽, 芦苇高出水面的部分,则水池的深度可以通过公式计算得到.请证明刘徽解法的正确性.
【题型6 应用勾股定理解决航海问题】
1.如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东方向开往B岛,其速度仍为20海里/小时.
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?(结果保留一位小数)
2.某日我海防巡逻艇在A处探测到在它正东方向距它30海里的B处有一艘可疑船只,该船只正以每小时36海里的速度沿北偏西方向行驶,巡逻艇立即沿北偏东的方向前往拦截,半小时后恰好在C处拦截到该船只.
(1)求巡逻艇的速度为每小时多少海里?
(2)求此时该船只所在处C与的距离为多少海里?
3.如图,一艘船由A岛沿北偏东方向航行至B岛,然后再沿北偏西方向航行至C岛.
(1)求A,C两岛之间的距离;
(2)确定C岛在A岛的什么方向?
4.如图,小岛A位于港口C北偏西方向上,小岛B位于港口C的北偏东方向上,且与港口C相距200海里,小岛B与小岛A相距250海里.
(1)求小岛A与港口C的距离;
(2)在小岛B处有一艘载满货物的货船,以每小时20海里的速度从小岛B出发沿B→A方向航行,当货船距离港口C最近时,求货船还需航行多长时间才能到达小岛A?
【题型7 应用勾股定理解决河的宽度】
1.如图,池塘边有两点,点是与方向成直角的方向上一点,测得长为米,长为米.求两点间的距离(取).
2.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点A处偏离欲到达地点B处,结果他在水中实际游的路程比河的宽度多.求该河的宽度的长.
3.如图,湖的两岸有两棵景观树,在与垂直的方向上取一点,测得米,米.求两棵景观树之间的距离.
4.如图,某渡船从点B处沿着与河岸垂直的路线横渡,由于受水流的影响,实际沿着航行,上岸地点C与欲到达地点A相距70米,结果发现比河宽多10米.
(1)求该河的宽度;(两岸可近似看作平行)
(2)设实际航行时,速度为每秒5米,从C回到A时,速度为每秒4米,求航行总时间.
【题型8 应用勾股定理解决台阶上地毯长度】
1.某学校为防止雨天地滑,需在一段楼梯台阶上铺上一块地毯,将楼梯台阶完全盖住.楼梯台阶剖面图如图所示,已知,,.
(1)求的长;
(2)若已知楼梯宽,每平方米地毯25元,需要花费多少钱地毯才能铺满所有台阶.(假设地毯在铺的过程中没有损耗)
2.如图,小明与小华爬山时遇到一条笔直的石阶路,路的一侧设有与坡面平行的护栏.小明量得每一级石阶的宽为,高为,爬到山顶后,小华数得石阶一共200级,若每一级石阶的宽和高都一样,且构成直角,请你帮他们求护栏的长度.
3.如图,楼梯的高度为,楼梯坡面的长度为,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?(精确到)
4.某会展中心在会展期间准备将高、长、宽的楼道铺上地毯,已知地毯每平方米30元,请你帮助计算一下,铺完这个楼道至少需要多少元?
【题型9 应用勾股定理解决汽车是否超速问题】
1.已知某高速路段限速(即).如图,汽车在车速检测仪A正前方30米的处,过了后到处,测得.请通过计算判断汽车是否超速.
2.某条道路限速,如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到车速检测仪A正下方的B处,过了,小汽车到达C处,此时测得小汽车与车速检测仪间的距离为.
(1)求的长;
(2)这辆小汽车超速了吗?
3.如图所示,点装有一车速检测仪,它到公路边的距离米,小汽车行驶过检测仪监控区域,到达点时开始计时,离开点时停止计时,已知米.
(1)若一辆汽车以的速度匀速通过监控区域,共用时几秒?
(2)若另一辆车通过监控区域共用时3秒,该车是否超速?请说明理由.
4.如图,一辆小汽车在一条道路上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方120米的处,过了8秒,小汽车到达处,此时测得小汽车与车速检测仪间的距离为200米.
(1)求的长;
(2)“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,这辆小汽车在段是否超速行驶?请说明理由(参考数据:)
【题型10 应用勾股定理解决是否受台风影响问题】
1.由于过度采伐森林和破坏植物,使我国许多地区频频遭受沙尘暴的侵袭.近日市气象局测得沙尘中心在市正西方向千米的处,以千米/时的速度向东偏南的方向移动,距离沙尘中心千米的范围是受沙尘暴严重影响的区域.
(1)问市会不会受到沙尘暴的严重影响?请通过计算说明理由;
(2)若受影响请计算市受影响的时间.
2.某市夏季经常受台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向由点行驶向点,已知点为一海港,当时,点到,两点的距离分别为和,以台风中心为圆心周围以内为受影响区域.
(1)海港受台风影响吗?为什么?
(2)若台风的速度为,则台风影响该海港持续的时间有多长?
3.如图,两条公路、交于点,在公路旁有一学校,与点的距离为,点(学校)到公路的距离为,一大货车从点出发,行驶在公路上,货车周围范围内有噪音影响.
(1)货车开过学校是否受噪音影响?为什么?
(2)若货车速度为,则学校受噪音影响多少秒钟?
4.2024年9月第11号台风“摩羯”登陆,使我国很多地区受到严重影响.据报道,这是今年以来对我国影响最大的台风,风力影响半径(即以台风中心为圆心,为半径的圆形区域都会受台风影响).如图,线段是台风中心从市移动到市的大致路线,是某个大型农场,且.若之间相距之间相距.
(1)判断农场是否会受到台风的影响,请说明理由;
(2)若台风中心的移动速度为,则台风影响该农场持续时间有多长?
【题型11 应用勾股定理解决选扯距离相离问题】
1.如图,铁路上有、两点(看作直线上两点)相距千米,、为两村庄(看作两个点),,,垂足分别为、,千米,千米,现在要在铁路旁修建一个煤栈,使得、两村到煤栈的距离相等.
设煤栈应建在距点千米处的点处,如图,则千米.
(1)(______)千米;
(2)煤栈应建在距点多少千米处?
2.如图,已知某学校A与直线公路相距300米(即米,),且与该公路上一个车站D相距500米(即米),现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市 C 与车站D的距离是多少米
3.如图,铁路上A,B两点相距,C,D两点为两村庄,于点A,于点B,已知,,现在要在铁路上建一个土特产收购站E,使得C,D两村到E站的距离相等,则E站应建在距A点多少千米处?
4.如图,小区A与公路l的距离米,小区B与公路l的距离米,已知米.
(1)政府准备在公路边建造一座公交站台Q,使Q到A、B两小区的路程相等,求的长;
(2)现要在公路旁建造一利民超市P,使P到A、B两小区的路程之和最短,求的最小值,求出此最小值.
【题型12 应用勾股定理解决几何图形中最短路径问题】
1.【实践发现】数学兴趣小组在研究蚂蚁在圆柱侧面爬行问题时,发现蚂蚁沿圆柱侧面从一点爬到另一点的最短路径问题与圆柱的展开图有关.
【实践探究】设计测量方案:
第一步:测量圆柱的底面半径,测得圆柱底面半径是2厘米;
第二步:测量圆柱的高,测得圆柱的高为4厘米;
第三步:如图,假设蚂蚁在圆柱侧面从点A爬到点B,研究其最短路径情况.
【问题解决】设蚂蚁爬行的最短路径长度为厘米,通过计算即可求得最短路径长度.
(1)根据题意知圆柱底面半径厘米,圆柱的侧面展开后是一个长方形(取3),其中一条直角边(圆柱侧面展开后长方形的高)为 厘米,另一条直角边(底面圆周长的一半)为 厘米;
(2)在展开图中,蚂蚁的最短路径是连接的线段长,请你计算蚂蚁从点爬到点的最短路程.
2.如图,长方体的底面边长分别为4cm和8cm,高为10cm,若一只蚂蚁从点开始经过4个侧面爬行一圈到达点,若蚂蚁的爬行速度为内蚂蚁能否爬到点?
3.【问题情境】
数学综合与实践活动课上,老师提出如下问题:一个三级台阶,它每一级的长、宽、高分别为20、3、2,和是一个台阶两个相对的端点.
【探究实践】
老师让同学们探究:如图①,若点处有一只蚂蚁要到点去吃可口的食物,那么蚂蚁沿着台阶爬到点的最短路程是多少?
(1)同学们经过思考得到如下解题方法:如图②,将三级台阶展开成平面图形,可得到长为20.宽为15的长方形,连接,经过计算得到长度为___________,就是最短路程.
【变式探究】
(2)如图③,是一只圆柱形玻璃杯,该玻璃杯的底面周长是,高是,若蚂蚁从点出发沿着玻璃杯的侧面到点,则蚂蚁爬行的最短距离为___________.-
【拓展应用】
(3)如图④,圆柱形玻璃杯的高,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在外壁上,离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所爬行的最短路程是多少?(杯壁厚度不计)(画出示意图并进行计算)
4.如图,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿剪开,所得的圆柱侧面展开图是______.
A. B. C. D.
(2)如图②,若将金属丝从点B绕四圈到达点A,则所需金属丝最短长度是多少?
(3)现有一个长、宽、高分别为的无盖长方体木箱(如图3,).现在箱外的点A处有一只蜘蛛,箱内的点C处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.(木板的厚度忽略不计)
参考答案
【题型1 应用勾股定理解决梯子滑落高度】
1.(1)解:在中,,,
由勾股定理得,
即,
解得:;
答:云梯顶端与墙角的距离的长为;
(2)解:,,
,
在中,,,
由勾股定理得,
即,
解得:,
,
.
答:云梯底端在水平方向上滑动的距离为.
2.解:如图所示,在中,根据勾股定理知,,
在中,,
根据勾股定理知,
.
答:梯子的端向上移动了.
3.(1)解:根据题意可知,,,
∴在中,
答:这个梯子的顶端距离地面.
(2)解:由题意得,,,
∴在中,
∴
答:梯子的顶端沿墙垂直下滑了.
4.(1)解:为长方形,
在中,由勾股定理
答:此时云梯顶端离地面的高度为9米
(2)解:,
在中,由勾股定理
答:消防车需要向建筑物方向移动4米到达B处.
【题型2 应用勾股定理解决旗杆高度】
1.(1)解:在中,
由勾股定理得,
所以,(负值舍去),
所以,(米),
答:风筝的高度为米;
(2)如图:由题意得,米,∴米,
∴,
∴米,
∴(米),
∴他应该往回收线7米.
2.解:设绳索长为x尺,则木桩高为尺,
∴在中,,,
∴根据勾股定理,得,
解得.
∴绳索长为尺.
3.(1)解:设旗杆的高度为米,则绳子的长度为米,
在中,由勾股定理得,,
解得,
答:旗杆的高度为米;
(2)解:由题意可知,米, 米,,
在中,由勾股定理得米,
∴米,
∴米,
答:此时绳结到地面的高度为米.
4.(1)解:由题意得,,
故答案为:;
(2)解:过点作,垂足为,
则,,
,
,
在中,,
,
即,
解得:,
答:秋千的高度为.
【题型3 应用勾股定理解决小鸟飞行的距离】
1.13
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题考查了勾股定理的应用,根据勾股定理,进行计算即可求解.
【详解】解:如图,
根据题意得:,
∴.
即喜鹊至少要飞.
故答案为:13
2.25
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题考查正确运用勾股定理.根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出即可.
【详解】解:如图,设大树高为米,小树高为米,
连接,平移到,则米,,两树相距米,
∴(米),
在中,(米),
故小鸟至少飞行米.
故答案为:25.
3.
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题主要考查了勾股定理的应用,根据“两点之间线段最短”可知:小鸟沿着两棵树的树梢进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出,熟练掌握其性质,合理添加辅助线是解决此题的关键.
【详解】如图,过C点作于E,则四边形是矩形,连接,
设大树高为,小树高为,
∴,,,
在中,
答:小鸟至少飞行米,
故答案为:
4.13
【知识点】求小鸟飞行距离(勾股定理的应用)
【分析】本题考查了勾股定理,过C作平行地面,连接,由题意得米,米,由勾股定理可得的长,即小鸟至少要飞行的距离.
【详解】解:过C作平行地面,连接,
由题意得,米,米,米,
由勾股定理得,米,
故答案为:13.
【题型4 应用勾股定理解决大树折断前的高度】
1.解:设竹子折断处离地面有尺,
由题意得:,,,,
∴,
则:,
解得:.
答:竹子折断处离地面有4.2尺.
2.(1)解:由题意,知.
因为,
设长为,则长,
则,
解得.
故旗杆距地面处折断;
(2)解:如图:
因为点P距地面,
所以,
所以,
则距离旗杆底部周围的范围内有被砸伤的风险,
所以在距离旗杆底部处有被砸伤的风险.
3.(1)解:两棵树的高度差为(米),两树相距米(米),
根据勾股定理可得:小鸟至少飞行的距离(米),
答:至少飞了米;
(2)解:由勾股定理得:,
,
解得:,
答:树折断处距离地面米.
4.(1)解:由题意可知:米,
,
,
又米,
,
米;
(2)解:点距地面米,
米,
(米.
【题型5 应用勾股定理解决水杯中的筷子问题】
1.解:如图,在中,,
根据勾股定理得
.
2.解:设,则,
由题意,得:,
解得:,即.
3.解:由题意可知 ABC是直角三角形,,,线段为内部底面圆直径,
内部底面圆半径为,
,
在中,
,
解得:或(舍去,不符合题意)
答:至少需要制作长的吸管.
4.(1)解:设水池深度为x尺,则芦苇高度为尺,
由题意有:尺;
为中点,且丈尺,
(尺);
在中,由勾股定理得:,
即,
解得:;
即尺;
答:水池的深度为12尺;
(2)证明:水池深度,则芦苇高度为,
由题意有:;
为中点,且,
;
在中,由勾股定理得:,
即,
整理得:;
表明刘徽解法是正确的.
【题型6 应用勾股定理解决航海问题】
1.(1)解:过点B作于点D,
在中,,设,则,
在中,,
则,,
由得,
解得,
,
答:港口A到海岛B的距离为海里;
(2)解:甲船看见灯塔所用时间:小时,
乙船看见灯塔所用时间:小时,
所以乙船先看见灯塔.
2.(1)解:,,,
,,
,
,,
∴在中,由勾股定理得,
,
答:巡逻艇的速度为每小时48海里;
(2)解:作于,
,
,
答:此时该船只所在处C与的距离为海里.
3.(1)如图,由题意可知:,
∵,
∴,
∴,
在中,,
答:A,C两岛之间的距离是;
(2)又∵,,
∴,
∵,
∴,
∴C岛在A岛北偏西的方向上.
4.(1)解:由题意得,,.
在中,,
∴.
答:小岛A与港口C的距离为150海里;
(2)解:过点C作于点D,
当货船航行到点D时,此时货船距离港口C最近.
∵,
∴,
在中,,
∴,
∴(小时).
答:货船还需航行4.5小时才能到达小岛A.
【题型7 应用勾股定理解决河的宽度】
1.解:由题意可得,
∵米,米,
∴米,
答:两点间的距离为米.
2.解:根据题意可知:设米,则米,
在中,,,
即,
解得:,
即米,
答.该河的宽度为75米.
3.解:在Rt中,由勾股定理,得:
,
(米).
答:两棵景观树之间的距离是12米.
4.(1)解:设米,则米,
在中,根据勾股定理得:
,
解得:,
答:河宽240米.
(2)解:(秒),
(秒),
(秒),
答:航行总时间为67.5秒.
【题型8 应用勾股定理解决台阶上地毯长度】
1.(1)解:∵,,,
,
答:的长为;
(2)解:地毯长为:,
∴地毯的面积为,
每平方米地毯25元,
需要花费(元);
答:需要花费元地毯才能铺满所有台阶.
2.解:根据勾股定理,每一级石阶的斜边长为,
.
答:护栏的长度为.
3.解:如图,由勾股定理得,,
∴米,
∴米,
答:地毯的长度至少需要米.
4.解:由勾股定理得,
则地毯总长为,
则地毯的总面积为(平方米),
所以铺完这个楼道至少需要(元).
故答案为:1020.
【题型9 应用勾股定理解决汽车是否超速问题】
1.解:汽车没有超速,理由如下:
依题意,由勾股定理可得:,,,
.
∴,
∴.
∴汽车没有超速.
2.(1)解:根据题意,得,,
由勾股定理,得,
∴,
故的长为.
(2)解:,
∵,
∴这辆小汽车未超速.
3.(1)解:依题意可得,,
∴,为直角三角形
∵米,米,
∴米,
,
∴
答∶共用时4秒;
(2)解:超速,理由如下∶
,
∵,
∴该车超速.
4.(1)解:在中,,
,
答:的长为米;
(2)解:小汽车的速度为:,
,
故小汽车超速了.
【题型10 应用勾股定理解决是否受台风影响问题】
1.(1)解:过点作于,由题意得千米,,
∴(千米),
∵,
∴市会受到沙尘暴的严重影响;
(2)解:设沙尘中心距点千米处,刚好处在上的两点,
在中,千米,千米,
∴千米,
∴千米,
∴市受影响的时间为(小时),
故市受影响的时间为小时.
2.(1)解:海港受台风影响,理由如下:
如图,过点作,
∵,
∴,
∵,,
∴,
∵,
∴,
∵以台风中心为圆心周围以内为受影响区域,
∴海港受台风影响;
(2)解:如图,假设当,时,正好影响港口,
∴,,
∴,
∵台风的速度为千米/小时,
∴(小时),
答:海港受台风影响的时间会持续小时.
3.(1)解:货车开过学校受噪音影响,理由如下:
∵,
∴货车开过学校受噪音影响;
(2)解:如图,设,则路段是学校受噪音影响的路段,
∵,
∴,
又,,
∴,
同理:,
∴,
∴影响时间,
答:学校受噪音影响时间是6秒.
4.(1)解:农场会受到台风的影响,理由如下:
如图,过作于,
,
,
,
的面积,
,
,
,
农场会受到台风的影响;
(2)解:如图,台风从点开始影响该农场,到点以后结束影响,连接,,
,
,
,
由勾股定理得,
,
台风中心的移动速度为,
台风影响该农场持续时间是(小时).
【题型11 应用勾股定理解决选扯距离相离问题】
1.(1)解:如图,连接,则,
∵,,
∴,
∵千米,
∴千米,
∵,
∴,
解得,
∴千米,
故答案为:;
(2)解:由()得,千米,
∴煤栈应建在距点千米处.
2.解:根据题意得:,,
在直角三角形中,
米,米,
(米),
设米,则米,
在中,,
即,
解得:,
答:该超市C与车站D的距离是312.5米.
3.解:,两村到站的距离相等.
,
于,于,
,
,,
,
设,则,
,,
,
解得:,
.
答:站应建在离站处.
4.(1)解:如图1,
根据题意得:,
设,则,
,
解得,
即的长为475米;
(2)如图,作点A关于直线l的对称点,连接,交直线l于点P.
则,
,
的最小值为,
如图,作于点E,
在中,
米,米,
米,
的最小值为1000米.
【题型12 应用勾股定理解决几何图形中最短路径问题】
1.(1)解:已知圆柱的高为4厘米,圆柱侧面展开后长方形的高就等于圆柱的高,所以其中一条直角边为4厘米,
已知圆柱底面半径厘米,取3,根据圆的周长公式,则底面圆周长的一半为厘米,即另一条直角边为6厘米,
故答案为:,;
(2)解:(厘米),
答:蚂蚁从点爬到点的最短路程厘米.
2.解:如图,将长方体的侧面展开在同一平面内,
,
.
,
,
内蚂蚁能爬到点.
3.解:(1)由题意得,
故答案为:;
(2)将圆柱体展开,由题意得
,
故答案为:;
(3)如图,
从玻璃杯侧面展开,作关于的对称点,作交延长线于点,连接交于点,
,,
,
,
,
蚂蚁从外壁处到内壁处所爬行的最短路程是.
4.(1)解:根据题意得:将圆柱侧面沿剪开,所得的圆柱侧面展开图只有选项A符合题意,
故选:A;
(2)若将金属丝从点B绕四圈到达点A,
则所需金属丝最短长度是以底面周长4倍及高为直角三角形的斜边长为:,
∴最短长度是;
(3)①把展开,如图此时总路程为,
②把展开,如图
此时的总路程为;
③如图所示,把展开,
此时的总路程为,
由于,所以第三种方案路程更短,最短路程为.
同课章节目录
