2026年中考数学复习课件 专题六 圆-微专题（十） 根据圆的基本性质作辅助线的方法 (共18张PPT)

(共18张PPT)
复习讲义
第一篇 考点精讲
专题六 圆
微专题（十） 根据圆的基本性质作辅助线的方法
方法一 构造等腰三角形
方法解读 连半径，利用“同圆的半径相等”构造等腰三角形，可以将线
段或角的问题转化到等腰三角形中解决.
方法应用
图1
1.（2024·山东·中考）如图1，是 的内接三角
形，若， ，则 的度数为____.
图1
提示：连接.因为 ，所以
.因为 ，所以
.因为 ，
所以 .所以
.
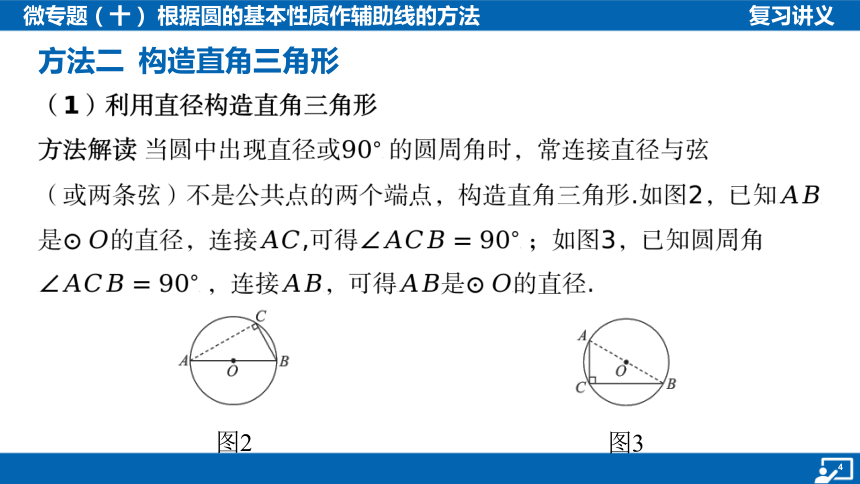
方法二 构造直角三角形
（1）利用直径构造直角三角形
方法解读 当圆中出现直径或 的圆周角时，常连接直径与弦
（或两条弦）不是公共点的两个端点，构造直角三角形.如图2，已知
是的直径，连接,可得 ；如图3，已知圆周角
，连接，可得是的直径.
图2
图3
方法应用
图4
2.（2024·黑龙江·中考）如图4，内接于 ，
是的直径.若 ，则 的度数为____.
提示：连接，因为 ，所以
.因为是 的直径，所以
.所以 .
图5
3.教材变式［人教版九上第89页第6题变式］如图5，一块
圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工
人师傅用直角尺作如图5所示的测量，测得 ，
，则圆形镜面的半径为___ .
提示：连接.由 ，且 是圆周角，可知
是圆形镜面的直径.在中， .故圆
形镜面的半径为 .
图6
（2）过圆心作弦的垂线段构造直角三角形
方法解读 在圆中，求弦长、半径或弦心距时，常过圆心
作弦的垂线段，再连接半径构造直角三角形，从而利用
勾股定理求解.在弦长、半径、弦心距三个量中，知二求
一.如图6，已知是的一条弦（不是直径），过点
作于点，连接，则，.
方法应用
4.如图7，的半径为5，是外一点，， ，则弦 的长为____.
图7
8
提示：如图38，过点作于点，连接，则 .在R中，， ，所以 .在R中，.因为 ，所以.
图38
方法三 构造同弧或等弧的圆周角（或圆心角）、构造圆内接
四边形
方法解读
1.构造同弧或等弧所对的圆心角或圆周角，利用圆周角定理及其推
论，可得角与角之间的数量关系.如图8，.如图9，.
图8
图9
2.构造圆内接四边形，可得两对互补的角.如图10，
， .
图10
方法应用
图11
5.如图11，点，，在上，若 ，则
的度数为( ).
A. B. C. D.
提示：如图39，在上取一点A，连接，.由四边形是 的内接四边形，得 .故 .
图39
A
微专题练习（十）根据圆的基本性质作辅助线的方法
方法一 构造等腰三角形
图1
1.（2025·江苏苏州·中考模拟）如图1，是 的内接三
角形，若 ，则____ .
62
提示：连接，则.所以 .
从而得 .故
.
2.如图2，为上的一点，为外的一点，交于点 ，且
， ，则 的度数为____.
图2
方法二 构造直角三角形
图3
3.如图3，是的直径，， ，
，则 的半径为( ).
D
A. B. C. D.
4.如图4，的直径和弦相交于点，， ， .求 的长.
图4
图53
解：如图53，过点作于点，连接
，，
.
在 中，， ， .
在 中，.
， .
方法三 构造同弧或等弧的圆周角（或圆心角）、构造圆内接
四边形
图5
5.（2025·浙江杭州·中考模拟）如图5，在中，半径 ，
互相垂直，点在劣弧上.若 ，则
的度数是( ).
D
A. B. C. D.
6.新情境问题 用破损的量角器按如图6方式测量的度数，让
的顶点恰好在量角器圆弧上，两边分别经过圆弧上的，两点.若点 ，
对应的刻度分别为 ， ，则 的度数为______.
图6
图54
提示：画出示意图如图54所示，其中 为量角器所在
圆，的直径为.设为优弧上一点，连接 ，
，，.由题意可知， ，
，从而得 .
所以 .故
.