2026年中考数学复习课件 专题四 三角形-微专题（八） 相似三角形的四种基本模型(共36张PPT)

(共36张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
微专题（八） 相似三角形的四种基本模型
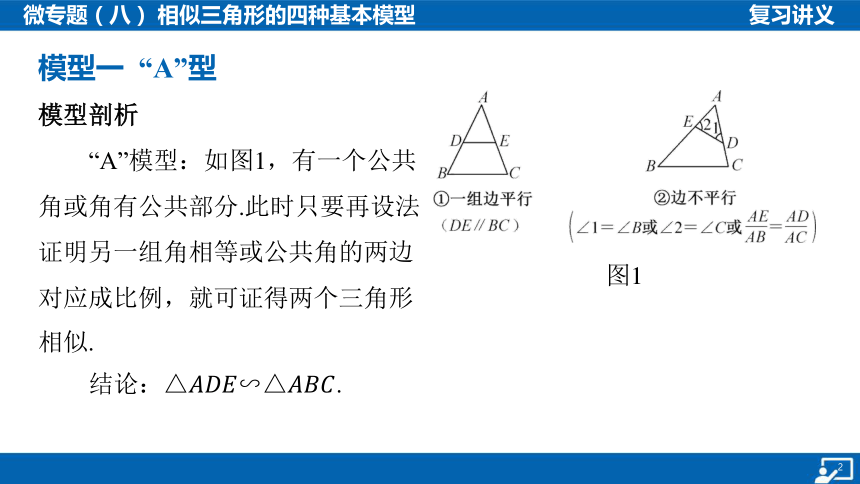
模型一 “A”型
图1
模型剖析
“A”模型：如图1，有一个公共
角或角有公共部分.此时只要再设法
证明另一组角相等或公共角的两边
对应成比例，就可证得两个三角形
相似.
结论： .
模型应用
图2
1.如图2，在中，于点， 于
点，连接 .
求证： .
证明：，， .
，
，即.
又∵ ， .
图3
2.（2025·浙江杭州·中考模拟）如图3，在 中，
点，，分别在边，，上，连接 ，
．已知四边形是平行四边形， ．
（1）当时，求线段 的长．
解：四边形是平行四边形，
.又， .
图3
（2）当的面积为1时，求 的面积．
解：， .
又，
四边形是平行四边形，，
， ..∴.
∴ ．
模型二 “X”型
图4
模型剖析
“”模型：如图4，有一组隐含的等
角（对顶角）.此时只要设法证明另一组
角相等或等角的两边对应成比例，就可
证得两个三角形相似.若题中未明确相似
三角形的对应点，则需要分类讨论.
结论： .
模型应用
图5
3.（2025·广西桂林·模拟）如图5，点， 分别在
，上，交于点， ，
，， .
（1）求证： .
证明：，.
又 ， .
图5
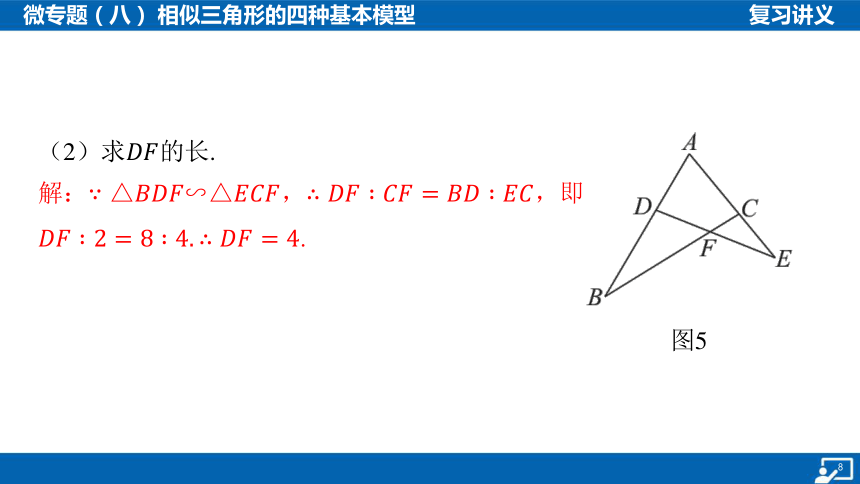
（2）求 的长.
解：， ，即
.
4.如图6，为的边的延长线上一点，分别交， 于点
， .
图6
（1）求证： .
证明：在中，，
.
（2）已知，，求 的长.
图6
解：在中，，
.
由（1）知，.
，， .
又， .
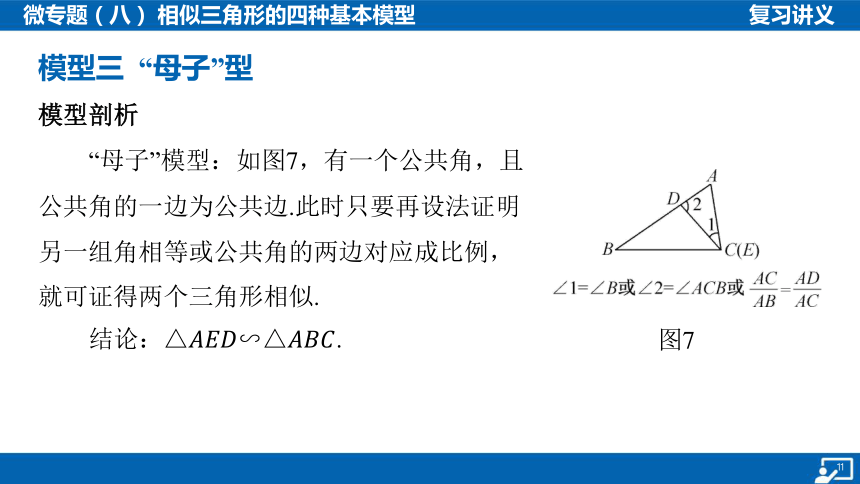
模型三 “母子”型
图7
模型剖析
“母子”模型：如图7，有一个公共角，且
公共角的一边为公共边.此时只要再设法证明
另一组角相等或公共角的两边对应成比例，
就可证得两个三角形相似.
结论： .
图8
【拓展】“三垂直”型
如图8，直角三角形被斜边上的高分成的两个直角三
角形与原三角形相似，即.
常见的结论有：，， .
模型应用
图9
5.如图9，在中， ， ，
的垂直平分线分别与，交于点，，连接 .
求证： .
证明：是的垂直平分线，
， .
， .
.
又 ， .
6.在中， ，点在上，且 .
图10
（1）求证： .
证明：，， .
（2）已知，，求 的长.
图10
解：，
， .
.
.
.
又，
，即.
（负值已舍去）.
模型四 “一线三等角”型
图11
模型剖析
“一线三等角”模型：如图11，
点在直线上，
（无论是锐角、直角,还是钝角），则 .“一线三等角”型
证相似，通常利用三角形内角和定理、邻补角的性质、平角的性质等证
两组角对应相等.
图12
【拓展】“一线三垂直”型
“一线三垂直”模型：如图12，点在直线
上， ，则
.
模型应用
图13
7.（2024·江西南昌·模拟）如图13，在等边三角形
中，是边上的动点（点 不与端点重合），
作 ，交边于点，交边 于
点 .
（1）求证： .
证明：是等边三角形，.∴
，∴
∴ .
图13
图13
（2）已知，， ，求
的长.
解： ，， ，∴ ，
， .
，即的长是 .
图14
8.（2025·甘肃武威·模拟）如图14，在矩形
中，为边上一点，把沿翻折，使点
恰好落在边上的点 处.
（1）求证： .
证明：四边形是矩形， .
.
由折叠的性质，得 .
.
∴ .
又 ， .
（2）已知，，求 的长.
图14
解： 四边形是矩形，， .
由折叠的性质，得.
在中，，
， ，即.
.
微专题练习（八） 相似三角形的四种基本模型
模型一 “A”型
图1
1.如图1，点，分别在的边， 上，且
，，.若使与 相似，
则 的长为_ ____.
图1
提示：①当时，，即 ，解
得当时，，即 ，
解得.综上可知，当的长为2或时， 与
相似.
答案：2或
图2
2.如图2，在锐角三角形中， ，高
，矩形的一边在边上，，
分别在，上，交于点 .
（1）当时，求 的长.
解： 四边形是矩形，
.
， .
， ∴ .
（2）当为何值时，矩形 的面积为150？
图2
解：由（1）可知，， .
令，解得
当时，矩形 的面积为150.
模型二 “X”型
3.如图3，四边形是平行四边形，则图中与 相似的三角形共
有( ).
B
图3
A.1个 B.2个 C.3个 D.4个
图4
4.（2025·甘肃天水·模拟）如图4，已知在
中，，点，分别在边， 的延长线
上，且，的延长线交于点 .
（1）求证： .
证明： ，
，，， .
又， .
图4
（2）当时，求证： .
解： ，，
，∴
，即 .
在和中，， ，，
.
模型三 “母子”型
图5
5.如图5，在中，是边 上一点，
，，， 的面积为4，
则 的面积为( ).
C
A.2 B.4 C.5 D.9
提示：由， ，得
.由此可得， .又，所以.故 .
图6
6.如图6，在中， ， 于点
，为线段上一点，且，过点 作
交于点，则线段，， 满足什么数
量关系？
解： ，， .
∴ .
∴
.
图6
. ，， ，
.
∴ .
， .
又∵ ，
，即 ．
模型四 “一线三等角”型
图7
7.如图7，已知点，，轴于点 ，
点为线段上一点，且.则点 的坐标为
( ).
A. B. C. D.
提示：因为，所以 .又
，所以 .又， 所以 .由此可得，即.解得.故 .
D
图8
8.（2024·山东东营·中考模拟）如图8， 为等边三
角形，点，分别在边，上， .
若，，则 的长为( ).
C
A.1.8 B.2.4 C.3 D.3.2
提示：由等边三角形的性质，得 ，
.所以 .因为
，所以 .从而得 .所
以.由此可得.因为，所以可设 ，
则，.所以.故 .
图9
9.如图9，在中，，点， 分别
是边，上的点，且 .
（1）求证： .
证明： ，
，
，
.
（2）当，，时，求 的长.
图9
解： ， ，即.
，∴
，即.
.
，
， . .