2026年中考数学复习课件 专题四 探究与证明(共81张PPT)

(共81张PPT)
复习讲义
第二篇 专题突破
专题四 探究与证明
类型一 类比探究类
类比探究类题目是一类共性条件与特殊条件相结合，由特殊情形
到一般情形（由简单情形到复杂情形）逐步深入，解题思想方法一脉
相承的综合性题目.这类题通常以几何综合题为主，具有条件类似、图
形结构类似和问法类似等特征.
类比探究类题目的解题思路：
（1）类比：类比是解决问题的第一原则，如类比字母、类比辅助
线和类比思想，即类比上一个问题的思路，迁移解决下一个问题.
（2）不变特征：对比前后条件变化，寻找并利用不变特征，考虑
相关几何结构解决问题.
（3）拓展、应用：会在类比探究类题目的最后一问中涉及，往往
要先依据特征转化作图（仿照前面问题的图形结构），依据图形的形
成因素设计方案，应用前面问题的解题思路或结论求解.
续表
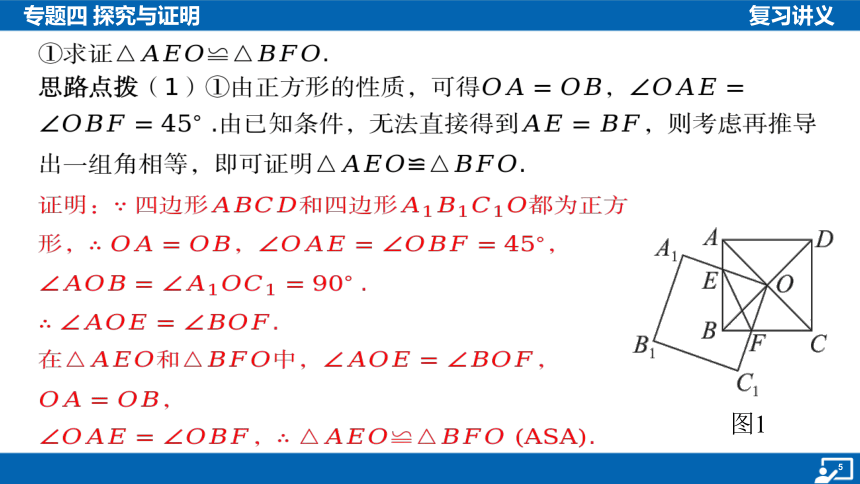
例1 （2025·广西南宁·模拟）几何探究
【课本再现】
（1）如图1，正方形的对角线相交于点，且点 是正方形
的一个顶点，这两个正方形的边长相等，边与边 相交于
点，边与边相交于点，连接 .在实验与探究中，小新发现无
论正方形绕点怎样转动，，，
之间一直存在某种数量关系，这种数量关系可以通过证明
推导出来.请帮助小新解答下列问题：
图1
图1
①求证 .
证明： 四边形和四边形 都为正方形，， ，
.
.
在和中，， ，
， .
思路点拨（1）①由正方形的性质，可得 ， .由已知条件，无法直接得到 ，则考虑再推导出一组角相等，即可证明 .
②，， 之间的数量关系是_________________.
图1
提示：由，得.又，所以 .在R中，由勾股定理，得，即 .
思路点拨 ②观察图形可发现，，， 不在同一直线，也不在同一个三角形中，则考虑根据全等三角形、正方形的性质，进行等量代换，将这三条线段转换到同一个三角形中，再结合三角形的相关性质、定理得出结论.
【类比迁移】
（2）如图2，矩形的中心是矩形的一个顶点， 与边相交于点，与边相交于点，连接，矩形 绕着点旋转，猜想，， 之间的数量关系，并进行证明.
图2
思路点拨 （2）类比（1）的解题思路，探究，， 之间的数量关系可构造全等三角形，将，， 等量转化到同一个三角形中.
图100
解：猜想： .
证明：如图100，延长交于点，连接
矩形的对角线相交于点， 是 的中点，即
四边形是矩形， ，
，.
在和 中，，
，，
，
四边形 是矩形， .
垂直平分 .
在 中，由勾股定理，得，即 .
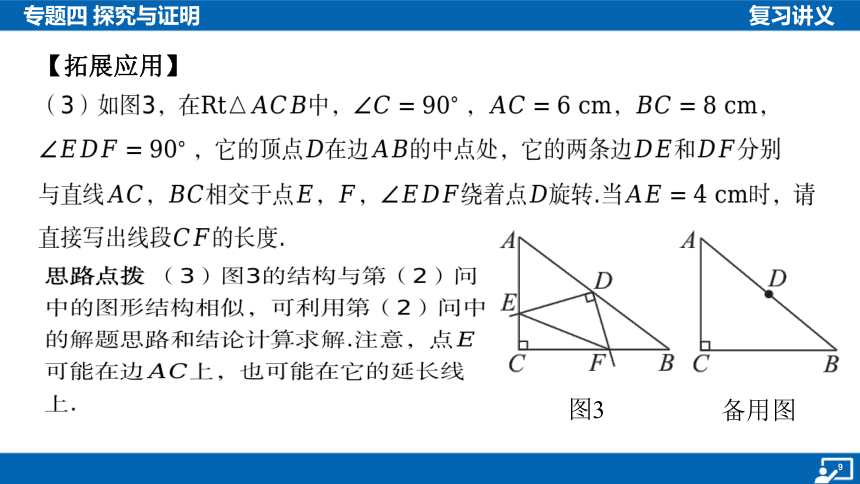
【拓展应用】
（3）如图3，在中， ，， ，
，它的顶点在边的中点处，它的两条边和 分别
与直线，相交于点，，绕着点旋转.当 时，请
直接写出线段 的长度.
图3
备用图
思路点拨 （3）图3的结构与第（2）问中的图形结构相似，可利用第（2）问中的解题思路和结论计算求解.注意，点可能在边 上，也可能在它的延长线上.
图101
提示：点为斜边的中点， ，根
据第（2）问中的结论可得，.当点 在
边上时，在 中，由勾股定理，得
.从而得 ，即
.解得 .如图101，当点
的长为或 .
在的延长线上时，过点作，交的延长线于点 ，连接
，.同理可得，即 .在
中，由勾股定理，得 .从而得
.解得.综上所述，的长为或 .
针对训练
图4
1.（2025·广西北海·模拟）探究与证明
【阅读材料】数学课上，老师提出了这样一个问题：如
图4，在正方形中，，分别是， 上的两点，
连接，交于点.已知，求证 .
甲小组同学的证明思路如下：
图4
由同角的余角相等可得.再由 ，
，证得 （依据：
____），从而得 .
乙小组的同学猜想，其他条件不变，若 ，则同
样可证得 ，证明思路如下：
由，可证得 . 由此可得
.再根据角的等量代换即可证得 .
（1）填空：上述材料中的甲小组同学的证明思路中的依据是_____
（填“”或“”或“”或“”或“ ”）.
【发现问题】同学们通过交流后发现，已知可证得 ；
已知同样可证得 .为了验证这个结论是否具有一般性，
又进行了如下探究.
【完成任务】
图4
【迁移探究】在正方形中，点在上，点，分别在，
上，连接，交于点 .
甲小组同学根据 画出图形如图5所示，
乙小组同学根据 画出图形如图6所示.
图5
图6
甲小组同学发现已知仍能证明 ，乙小组同学发现已
知无法证明 一定成立.
（2）①在图5中，已知，求证 .
证明：如图107，过点作于点
四边形是正方形， ， .
四边形是矩形.
， .
.
∵ ， . .
在和中，， ，， .
图5
图107
②在图6中，若 ，则 的度数为多少
解：如图108，过点作于点 ，同理可得四边形是矩形.
.
在 和R中，，，∴
.
图6
图108
【拓展应用】
图7
（3）如图7，在正方形中， ，
点在边上，点在边 上，且
，点，分别在直线 ，
上，.当直线与直线 所
夹较小的角的度数为 时，请直接写出
的长.
图109
提示：①当，分别在边，边 上时，如图109， ，过点作于点，过点 作于点，交于点，则四边形 和四边形 都是矩形. 同理可证 ，
. ，
. ，
. .
.
图110
的长为或 .
②当点，分别在， 的延长线上时，如图110. 同理可得 ，. .
类型二 操作探究类
操作探究类题目是指通过动手测量、作图、取值、计算等试验，
猜想获得数学结论的探索研究性活动.这类题目模拟以动手为基础的手
脑结合的科学研究模式，需要动手操作、合理猜想和验证，包含观
测、操作、猜想、收集整理、思考、推理、交流和应用等形式.解决这
类问题可以通过动手操作，将复杂的问题直观化、简单化.
典题精析
例2 （2025·九江·中考模拟）探究与证明
折纸，操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘.
【动手操作】如图8，将矩形纸片对折，使与 重合，展平纸片，得到折痕；折叠纸片，使点落在上，并使折痕经过点，得到折痕 ，点，的对应点分别为，，展平纸片，连接，， .请完成：
图8
（1）观察图8中的，和 ，试猜想这三个角的大小关系.
图8
【答案】猜想： .
思路点拨（1）可通过观察、度量或推理得出猜想.
（2）证明（1）中的猜想.
证明：在矩形中，.
将矩形纸片对折后， 与重合， ，
∴
∵ 将矩形纸片沿 折叠后，点的对应点为，
∴
∴ 是等边三角形.∴ .
图8
思路点拨 （2）只要利用折叠的性质，得到是等边三角形，进而求出，， 的度数，即可得出结论.
∴ .
由折叠的性质知，点，与点，分别关于对称，又，∴
∴ .
∴ .
图8
图9
【类比操作】
如图9，为矩形纸片的边上的一点，连
接，在上取一点，折叠纸片，使，两
点重合，展平纸片，得到折痕；折叠纸片，使
点，分别落在，上，得到折痕，点，
的对应点分别为，，展平纸片，连接，
.请完成：
（3）证明是 的一条三等分线.
证明：如图102，连接 .
将矩形纸片折叠后，，两点重合，折痕为， ， .
是的垂直平分线.
图102
思路点拨 （3）如果能证明 ，就可以推出，证得结论.连接，通过证明 ，得出 ，再根据折叠的性质、等腰三角形的性质和平行线的性质，推出，即可证明 .
，，
将矩形纸片沿折叠后，点， 的对应点分别为，， 点，分别与点，关于对称.
∴ ，.
在和中， ，，，
∴
图102
是 的一条三等分线．
图102
针对训练
2.（2025·甘肃兰州·中考模拟）
【观察发现】劳动人民在生产生活中创造了
图10
很多取材简单又便于操作的方法，例如木匠刘师傅的“木条画直角法”，如图10，他用木条能快速画出一个以点 为顶点的直角，具体作法如下：
①木条的两端分别记为点，，先将木条的端点与点 重合，任意摆
放木条后，另一个端点的位置记为点，连接 ；
②木条的端点固定在点处，将木条绕点 顺时针旋转一定的角度，端
点的落点记为点（点，， 不在同一条直线上）；
③连接并延长，将木条沿点到点的方向平移，使得端点与点 重
合，端点在延长线上的落点记为点 ；
图10
④用另一根足够长的木条画线，连接，，则画出的 是直角.
【操作体验】
（1）根据“观察发现”中的信息重现刘师傅的画法，如图11， ，
请画出以点为顶点的直角，记作 .
图11
解：如图111.
图111
【推理论证】
（2）如图10，小亮尝试揭示此操作
的数学原理，请你补全括号里的证
明依据.
证明： ，
与 是等腰三角形.
， （依据1：_______________________
__________）.
等边对等角（等腰三角形的性质）
图10
（依据2：__________________），
，
. .
三角形内角和定理
图10
【拓展探究】
（3）小亮进一步研究发现，用这种方法作直角存在一定的误差，而用平时学习的尺规作图的方法可以减少误差.如图12，点在直线 上，请用无刻度的直尺和圆规在图12中作出一个以 为顶点的直角，记作，使得直角边（或）在直线 上.（保留作图痕迹，不写作法）
图12
解：如图112.
图112
类型三 猜想论证类
猜想论证类探究题的解题思路：先分析归纳题目中的图形、数和
式子，发现它们的共同特征或发展变化的趋势，再由此猜想它们之间
的规律或相关结论，并运用所学知识证明猜想所得结论的正确性.这类
问题的解题方法灵活多样，可能会用到计算、验证、类比、比较、测
量等.解题时要结合题目给出的条件进行猜想，然后运用数学知识进行
合理的推理论证.
典题精析
例3 （2024·江苏扬州·中考）在综合实践活动中，“特殊到一般”是一种
常用方法，我们可以先研究特殊情况，猜想结论，再研究一般情况，证
明结论.
如图13，已知，，是的外接圆，点在
上，连接，， .
图13
备用图
【特殊化感知】
（1）如图13①，若 ，点在的延长线上，则
与 的数量关系为_______________.
图13
提示：，， 为等边三角形. . . 为 的直径， .
.
思路点拨（1）由 ，，可得 是等边三角形. 观察图形，发现是的直径且是和 的公共边，由圆周角定理的推论，可得 .那么我们便可以在R，中探索，，之间的数量关系.
【一般化探究】
（2）如图13②， ，点，在同侧，判断 与
的数量关系，并说明理由.
图13
思路点拨 （2）与 有相同的已知条件“ ， ”，猜想（1）中结论依然成立.由于不一定是 的直径，无法确定直角三角形，则考虑构造全等三角形来探究线段之间的数量关系.
图103
解： .
理由：（方法一）如图103，延长至点使 ，连接
， ， 为等边三角形.
.
四边形 为的内接四边形， .
又， 为等边三角形.
， .
，
，
， .
在 和中，，，，
， ，即
.
图103
图104
（方法二）理由：如图104，在上截取 ，连接.
同理可得 是等边三角形，
，即
.
【拓展性延伸】
（3）已知 ，直接写出，与 满足的数量关系.
（用含 的式子表示）
图13
思路点拨 （3）题设没有限定点， 的位置，则点，可能在同侧，也可能在 两侧，因此需要分两种情况讨论. 而 不是特殊角，于是猜想，，满足的数量关系与 的大小有关，可考虑构造直角三角形来沟通边角关系，用含三角函数的式子表式它们的数量关系.
图105
提示：①如图105，当点，在同侧时，延长 至点
，连接，使，过点作于点
， ，
四边形为的内接四边形，
， ， ，∴ ，
，
，
，
.在和中， ，
，，
，
.
图105
图106
②如图106，当点，在两侧时，延长至点 ，
使，连接，过点作于点 .
， ，
四边形为 的
内接四边形， .在和
中，，，，
，，
， ，
，
， .
【答案】当点，在同侧时， ；当点 ，
在两侧时， .
图106
针对训练
3.【观察分析】
（1）观察下列两个数的乘积：，，， ，，
（两个乘数的和为10），猜想其中哪两个数的乘积最大（只写出结论即
可）．
提示：，，，， ，
，，，，故 最大.
答案：5与5的乘积最大.
（2）观察下列两个数的乘积：，，， ，
， （两个乘数的和为100），猜想其中哪两个数的乘积
最大（只写出结论即可）．
提示：，， ，
，， ，
，， ，
， 依此可推出 最大.
【答案】50与50的乘积最大.
【猜想验证】
（3）根据上面活动给你的启示，猜想如果两个正数的和为
（其中 ），那么这两个数分别为多少时，两个乘数的乘积最大.用
二次函数的知识说明你的猜想的正确性．
解：猜想：已知两个正数的和为，当这两个数分别为， 时，乘积最大.
理由如下： 设其中一个数为，则另一个数为 ，它们的乘积为.
根据题意，得 .
因此，当时，取得最大值，为 .
【拓展应用】
图14
（4）用长度为 的竹签制作一个四边形风筝，如图14，
，是风筝的骨架，且 ，为了使风筝在空中能获
得更大的浮力，要把风筝的面积（四边形 的面积）制作
到最大．根据上面的结论，求当风筝的骨架， 的长分别
为多少时，风筝的面积能达到最大？
解：设，则，风筝的面积为 .
根据题意，得 .
因此，当时， 取得最大值，为.
故当 时，风筝的面积能达到最大．
专题练习四 探究与证明
类型一 类比探究类
1.（2024·甘肃·中考）【模型建立】
图1
（1）如图1，已知和，， ，
，.用等式写出线段，， 的数量
关系，并说明理由.
解：.
理由： ， ，
， .
.
.
在和中，，，，
，
，∴ ，即 .
图1
【模型应用】
（2）如图2，在正方形中，点，分别在对角线和边 上，，.用等式写出线段，， 的数量关系，并说明理由.
图2
图128
解：.
理由：如图128，过点 作于点，过点作于点
四边形是正方形， ， ，即平分
，， .
在和中， ，
，
，，， 四边形是正方形.
，
，∴
，∴
.
图128
【模型迁移】
（3）如图3，在正方形中，点在对角线上，点在边 的延长线上，，.用等式写出线段，， 的数量关系，并说明理由.
图3
解：.
理由：如图129，过点 作于点，过点作，交 的延长线于点
，，， .
.
图129
图129
∴ .
在和 中，，，，
∴
四边形是正方形， .
.
， ，
，，
.
图129
2.（2024·湖北武汉·中考）【问题背景】
图4
（1）如图4，在矩形中，点，分别是 ，
的中点，连接，.求证： .
证明： ，分别是和的中点， .
四边形 是矩形，
，
.
.
【问题探究】
（2）如图5，在四边形中，， ，点是 的中点，点在边上，，与相交于点.求证： .
图5
证明：（方法一）如图130，延长交的延长线于点，过点作 于点，则四边形是矩形.
，
是的中点，
， ， .
图130
图130
在和中， ，，，
，，
，即.
在和中，， ，，
.
又 ，
.
图131
（方法二）如图131，取的中点，连接 ，
是的中点，是的中点， ，
，
，
四边形 是平行四边形.
∴
， 是的中点，
.
【问题拓展】
（3）如图6，在“问题探究”的条件下，连接，， . 请直接写出 的值.
图6
图132
提示：如图132，过点作于点，取 的中
点，连接，，则四边形 是矩形.
， .设，则 ，， ，又由（2）知， .又是的中点， 垂直平分
.
是中点， 是的中位线.
，
.
图132
类型二 操作探究类
3.（2025·贵州·中考模拟）综合与探究
如图7， ，点在的平分线上，于点 .
图7
【操作判断】
（1）过点作于点，根据题意在图7①中画出，图中
的度数为____.
图7
解：如图133， 即为所求作，
图133
【问题探究】
（2）如图7②，点在线段上，连接，过点作 交射线
于点.求证： .
图7
图134
证明：如图134，过点作于点， .
又， ， 四边形是矩形.
.
点在 的平分线上，
矩形是正方形.
∴
，.
在和 中，，，，∴
∴
∴ .
【拓展延伸】
（3）点在射线上，连接，过点作交射线于点 ，
射线与射线相交于点.当时，求 的值.
图7
图135
解：①如图135，当点在线段 上时，延长，交于点 .
由（2）知，.
设 ，则，
.
在和中， ，
，，
，
，即. .
图136
②如图136，当点在 的延长线上时，过点作于点，并延长交于 .
由（2）知，四边形是正方形，∴ ， ，
，.
在和中， ，
，，
.
设 ，则， ，
，
，即.
∴ .
，
∴ ，即.
.
综上所述，的值为或 .
图136
类型三 猜想论证类
图8
4.（2025·驻马店·模拟）联想与思考
【提出问题】同学们已经研究过锐角三角形面积
与内切圆半径之间的关系，即：如图8，在锐角三角
形中，，，的对边分别是，， ，设
的内切圆的半径为，的面积为 ，
则 .小明在学习了以上的知识后提出了另
一个问题：任意一个锐角三角形都有内切圆与外接圆，那么锐角三角形
的面积 与它的外接圆半径有怎样的关系呢？
【分析问题】为解决该问题，老师让同学们进行了如下的思考与探究：
图8
图9
（1）如图9，设锐角三角形的外接圆的半径为 ，
同学们提出猜想： .在证明的过程中，同学们
发现该猜想的结论与 有关，由此启发：添加辅助线
构建直角三角形来解决问题.小明经过思考做了以下尝试，
请你补全证明过程：
证明：如图9，连接并延长交于点，连接 .
___，____ .
_____ .
.
90
（2）请你根据上述启发，结合图10，求证： .
图10
证明：过点作于点.
在中，，∴
.
【解决问题】
图8
（3）结合（1）（2）的结论，请探究锐角三角形的
面积与它的外接圆半径之间的关系（用含有 ，
，和的式子表示 ），并说明理由.
解：.
理由：由（1）（2）可知 ，， .
图11
5.中考预测题【问题情境】 如图11，是线段 上任
意一点（点不与点，重合），分别以和 为
斜边在同侧构造等腰直角三角形 和等腰直角三
角形，连接.取的中点，的中点 ，连接
．
图12
（1）如图12，当点与点重合时，试判断与 之间的数量关系，并说明理由.
解：．
理由如下： ， 都是等腰直角三角形， ，，
，
.
∴ .
又 是的中点，∴
，即 ．
【猜想验证】
【延伸探究】
（2）如图13，当点与点 不重合时，问题（1）中的结论是否仍然成
立？若成立，则写出证明过程；若不成立，则说明理由.
图13
图137
解：问题（1）中的结论仍然成立．理由如下：如图137，延长交的延长线于点，连接 ，
，都是等腰直角三角形，∴ ，，
， .
，
四边形 是矩形，是等腰直角三角形.
是的中点， ，即 .
是的中点， 是的中点.
在中， 是的中点，
，即 ．
图11
（3）如图13，若，线段 是否存在最小值？
若存在，则直接写出最小值；若不存在，则说明理
由．
提示：如图137，在中，是的中点，
.由（2）可知，，
【答案】的最小值为 .
，即. 的最小值为 .由（2）知，
， 的最小值为 ．